【贪心算法】Dijkstra 算法及其衍生

Dijkstra 算法

1959 年，Edsger Dijkstra 提出一个非常简单的贪心算法来求解单源最短路径问题（Single-Source Shortest Path，SSSP）。

我们开始来描述这个算法，它确定从源点s 到图的每个其他结点的最短路径的长度，同时也容易确定这些路径。算法维护结点的集合 $S$ ，对于这些结点我们已经确定了从 s 出发的最短距离 d(u)。

1. 这是图“已被探查”的部分初始：$S=\{s\}$ ，且 $d(s)=0$ 。

2. 现在对每个结点 $v\in V-S$ 我们确定一条最短路径，它可以沿一条穿过已被探查部分 S 的路径旅行到某个 $u\in S$ ，然后再沿着一条边 $(u,v)$ 而把这条路径构造出来，即我们考虑量 $d^{\prime }(v)={\min }_{e=(u,v):u\in S}d(u)+l_e$ 。

3. 我们选择结点 $v\in V-S$ 使得这个量最小，将 $v$ 加到 $S$ 中，并且定义 $d(v)$ 是 $d^{\prime }(v)$的值。

生成与 Dijkstra 算法找到的距离相对应的 s➡u 路径 $P_u$ 是简单的：

• 当每个结点 $v$ 被加到集合 $S$ 时，只需要记录一条达到值 ${\min }_{e=(u,v):u\in S}d(u)+l_e$ 的边 $(u,v)$
  路径 $P_v$ 隐含地由这些边描绘出来：
  • 为构造 P_v，我们只不过从 $v$ 开始，沿反方向跟随对 $v$ 存入的边到 $u$
    然后沿反方向跟随对 $u$ 存入的边到它的祖先，并且继续下去直到我们到达源点 $s$ 。

---

Dijkstra 算法正确性

证明算法的正确性即证明路径 $P_u$ 确实是最短路径。

Diikstra 算法在下述意义上是贪心法，我们用一条边加上一支在 S 中的路径总可以构造一支最短的新的 s-v 路径。通过归纳证明它“领先于”所有其他的解，即确定每一次它选了一条到结点 $v$ 的路径，这条路径比每条到的其他可能的路径都要短。

证明

通过在 S 的大小上的归纳来证明这个定理；

• $|S|=1$ 此时有 $S=s$ 和 $d(s)=0$
• 当 $|S|=k,k\ge 1$ 时，加入结点 $v$ 使得 $|S|=k+1$ ，令 $(u,v)$ 是路径上的最后一条边

根据归纳假设：路径 $P_u$ 是对某个结点 $u\in S$ 的最短 s-u 路径
考虑任意其他的 s-v 路径 $P$，要证明它至少与 $P_v$ 一样长，为了到达 $v$ ，这条路径 $P$ 一定在某个地方离开集合 $S$ ：

设 $y$ 是在 $P$ 上但不在 $S$ 中的第一个结点，且设 $x\in S$ 是紧接在 $y$ 前面的结点，如下图所示

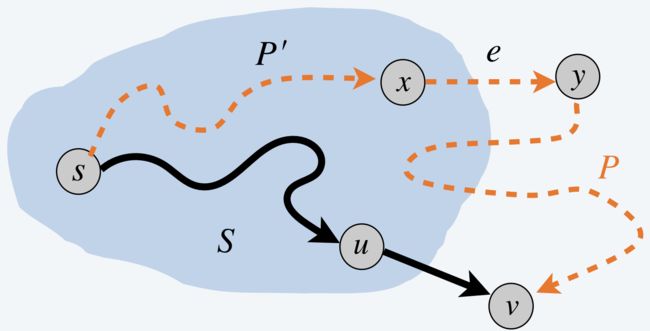
证明的关键非常简单：$P$ 不可能比 $P_v$ 短，因为到它离开集合 $S$ 的时刻至少已经与 $P_v$ 一样长。在第 $k+1$ 次选代中，Diikstra 算法一定已经考虑过通过边 $(x,y)$ 把结点 $y$ 加到 $S$ 中，但是由于加 $v$ 更有利而放弃了这个选择。这就意味着没有从 $s$ 经过到 $y$ 且比 $P_v$ 更短的路径。同时 $P$ 中到 $y$ 为止的子路径是至少与 $P_v$ 一样长的路径

令 $P^{\prime }$ 代表 $P$ 的从 $s$ 到 $x$ 的子路径。

• 因为 $x\in S$ ，根据归纳假设 $P_x$ 是最短的 s-x 路径，且长度为 $d(x)$ ，因此 $l(P^{\prime })\ge l(P_x)=d(x)$

• 于是 $P$ 的到结点 $y$ 的子路径 $l(P)$ 有长度 $l(P^{\prime })+l(x,y)\ge d(x)+l(x,y)\ge d^{\prime }(y)$

• 因为 Dijkstra 算法在这次迭代中选择了 $v$ 而不是 $y$ 所以 $d^{\prime }(y)\ge d^{\prime }(v)=l(P_v)$ 。

上述不等式组合起来可证明： $l(P)\ge l(P^{\prime })+l(x,y)\ge l(P_v)$

---

Dijkstra 算法的复杂度

• 对于具有 $n$ 个结点的图：While 循环的迭代有 $n-1$ 次，每次迭代把一个新结点 $v$ 加到 $S$ 中。有效选择正确的结点 $v$ 是比较复杂的事情。如果考虑每个结点 $v\in S$ 并且检查所有在 $S$ 与 $v$ 之间的边以确定最小值
• 对于具有 $m$ 条边的图，计算所有这些最小值可能用 $O(m)$ 时间
• 运行时间为 $O(mn)$

优化

对于最小值的确定可以采取一定的优化措施
对每个结点 $v\in V-S$ 维护最小值 $d^{\prime }(v)={\min }_{e=(u,v),u\in S}d(u)+l_e$ ，而不是在每次迭代时重新计算
同时将 V-S 的结点保存在一个以 $d^{\prime }(v)$ 作为其关键字的优先队列里来进一步改进算法的效率

• 优先队列：用于维护 n 个元素集合的数据结构，每个元素具有一个关键字。一个优先队列可以有效地插入元素、删除元素、改变一个元素的关键字以及取出具有最小关键字的元素。

使用优先队列，Dijkstra 算法可以在具有 n 个结点和 m 条边的图上，实现运行在 $O(m)$ 时间，加上 n 次 ExtractMin 操作和 m 次ChangeKey 操作的时间.

每个优先队列的操作可以运行在 $O(\log n)$ 时间

于是对于这个实现的总时间是 $O(m\log n)$

import heapq

def dijkstra(graph, start):
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        if current_distance > distances[current_node]:
            continue

        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

# Example graph
graph = {
    'A': {'B': 4, 'C': 2},
    'B': {'A': 4, 'C': 5, 'D': 10},
    'C': {'A': 2, 'B': 5, 'D': 3},
    'D': {'B': 10, 'C': 3}
}
start_node = 'A'

result = dijkstra(graph, start_node)
print("Shortest distances from node", start_node, "to all other nodes:", result)

---

Dijkstra 算法的衍生

priority queue	INSERT	DELETE-MIN	DECREASE-KEY	total
Node-indexed array (A[i] = priority of i)	$O(1)$	$O(n)$	$O(1)$	$O(n^2)$
Binary heap	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(m\log n)$
D-way heap (Johnson 1975)	$O(d{\log }_{d}n)$	$O(d{\log }_{d}n)$	$O({\log }_{d}n)$	$O(m{\log }_{m/n}n)$
Fibonacci heap (Fredman–Tarjan 1984)	$O(1)$	$O(\log n)$	$O(1)$	$O(m+n\log n)$
Integer priority queue (Thorup 2004)	$O(1)$	$O(\log \log n)$	$O(1)$	$O(m+n\log \log n)$

---

SSSP的应用

• PERT/CPM（计划评审技术/关键路径法）
• 地图导航
• 缝隙雕刻（Seam Carving）
• 机器人导航
• 纹理映射
• LaTeX排版
• 城市交通规划
• 电话营销员排班
• 电信消息路由
• 网络路由协议（OSPF, BGP, RIP）
• 根据给定交通拥堵模式的最佳卡车路线

---