【网络安全】【密码学】【北京航空航天大学】实验二、数论基础（中）【C语言和Java实现】

实验二、数论基础（中）

一、实验内容

1、扩展欧几里得算法（Extended Euclid’s Algorithm）

（1）、算法原理

已知整数 a , b ,扩展的欧几里得算法可以在求得 a , b 的最大公约数的同时，找到一对整数 x , y ,使得 a , b , x , y 满足如下等式：ax + by = d = gcd(a,b)， 其中 gcd(a, b) 为 a 和 b 的最大公约数。

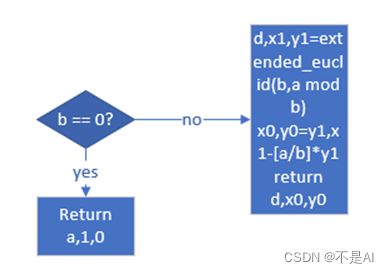
（2）、算法流程

本算法的大致流程如下图所示：

（3） 算法的代码实现（C语言）

# include 

int r2, s2, t2;

void Extended_Euclid(int a, int b);

int main(){
    int a, b;
	printf("请输入整数a:\n");
	scanf("%d", &a);
	printf("请输入整数b:\n");
	scanf("%d", &b);
	Extended_Euclid(a, b);
	printf("a和b的最大公因子为: %d\n", r2);
	printf("满足ax + by = gcd(a, b)的因子x和y分别为: %d %d\n", s2, t2);
	return 0;
}
	
void Extended_Euclid(int a, int b){
    int r, s, t;
	int r1, s1, t1;
	int tmp1, tmp2, tmp3;
	int q;
	r = a;
	s = 1;
	t = 0;
	r1 = b;
	s1 = 0;
	t1 = 1;
	while(r1 != 0){
	    q = r / r1;
		tmp1 = r - q * r1;
		tmp2 = s - q * s1;
		tmp3 = t - q * t1;
		r = r1;
		s = s1;
		t = t1;
		r1 = tmp1;
		s1 = tmp2;
		t1 = tmp3;
	}
	r2 = r;
	s2 = s;
	t2 = t;
	return;
}

（4）、算法测试

测试点1：a = 7, b = 5

测试点2：a = 31, b = -13

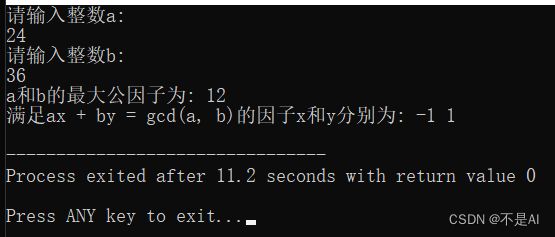
测试点3：a = 24, b = 36

（5）、一点思考

线性系数x和y不是唯一的，比如样例3中既可以是24 * (-1) + 36 * 1 = 12,也可以是24 * 2 + 36 * (-1) = 12. 如何能使算法找出所有满足条件的解？

2、简单幂取模算法（Simple Exponentiation-Module Algorithm）

（1）、算法原理

每次做乘法操作时都取模，即“乘一次模一次，循环往复”。数学表达式为 d = (((x^(n-1))mod m)*x) mod m

（2）、算法流程

本算法的大致流程如下图所示：

（3）、算法的代码实现（C语言）

#include 


int main(){
	int x, n, m;
	int ans;
	int i;

    printf("请输入底数x的值：\n");
	scanf_s("%d", &x);

    printf("请输入指数n的值：\n");
    scanf_s("%d", &n);

    printf("请输入模数m的值：\n");
    scanf_s("%d", &m);

	ans = 1;
	
	for(i = 1;i <= n;i ++)
    {
		ans = (ans * x) % m;
	}
	
	printf("%d", ans);
	
	return 0;
}

（4）、算法测试

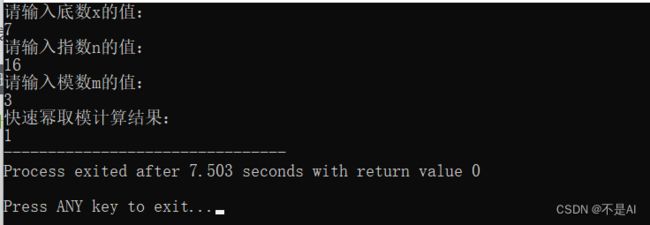
测试点1：x = 7, n = 16, m = 3

运行时截图：

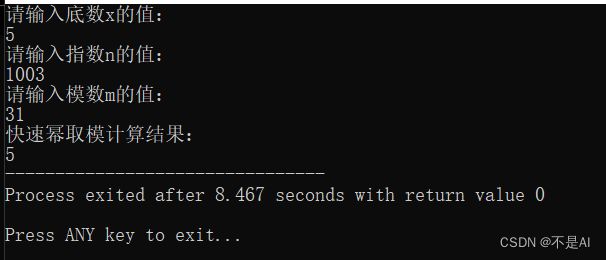
测试点2：x = 5, n = 1003, m = 31

运行时截图：

2、快速幂取模算法（Fast Exponentiation-Module Algorithm）

（1）、算法原理

常规的幂取模算法包含过多的乘法以及取模运算，计算步骤多，导致算法的效率很低。根据模运算和幂运算的性质，可以将幂次（指数n）用2进制进行表示，然后再迭代进行求模幂，从而减少乘法和取模的次数。

（2）、算法流程

本算法的大致流程如下图所示：

（3）、算法的代码实现（C语言）

#include 


int main()
{
	int x, n, m;
	
	int d = 1;
	
	printf("请输入底数x的值：\n");
	scanf_s("%d", &x);
	
	printf("请输入指数n的值：\n");
	scanf_s("%d", &n);
	
	printf("请输入模数m的值：\n");
	scanf_s("%d", &m);
	
	while(n > 0)
	{
		if((n % 2) == 1)
		{
			d = (d * x) % m;
			n = (n - 1) / 2;
		}
		else
		{
			n = n / 2;
		}
		x = (x * x) % m;
	}
	
	printf("快速幂取模计算结果：\n");
	printf("%d", d);
	
	return 0;
}

（4）、算法测试
测试点1：x = 7, n = 16, m = 3

运行时截图：

测试点2：x = 5, n = 1003, m = 31

运行时截图：

二、参考文献

1、《密码编码学与网络安全——原理与实践（第七版）》（Cryptography and Network Security, Principles and Practice, Seventh Edition），【美】威廉 斯托林斯 William Stallings 著，王后珍等 译，北京，电子工业出版社，2017年12月。

2、《密码学实验教程》，郭华 刘建伟等 主编，北京，电子工业出版社，2021年1月。