计算机体系结构----指令集与简单CPU处理器设计（二）

本文仅供学习使用，严禁转载。本文参考资料来自中国科学院大学计算机体系结构课程PPT，以及计算机体系结构量化研究方法（第6版）

本文主要对计算机组成原理做一个简要的复习，方便后续深入整个计算机体系结构。

处理器及其组件

Processor (CPU): 执行指令集架构中的指令。

• 数据通路（DataPath）：处理器中包含执行处理器需要的操作必要硬件部分。
  简单说就是指令执行过程中，数据所经过的路径上的部件。一般包括逻辑运算部件（ALU）、寄存器堆（Register File/ RegFile/ RF）。
• 控制部件（Control Unit）：处理器中告诉数据通路需要做什么的部件。
  控制部件对指令进行译码，生成指令对应的控制信号，控制数据通路的动作。
  控制器是指令的控制部件，对执行部件发出这些控制信号。

衡量处理器性能的一个角度

处理器内部的数据通路和控制设计将对时钟周期（clock cycle time）和每条指令所花的时钟数（clock cycles per instruction/CPI） 产生影响。

CPUTime = InstructionCount × CPI × Cycle Time (ET = IC × CPI × Cycle Time)
CPU的执行时间表示成指令数乘以每条指令所花的时间

指令数目（InstructionCount/IC）由编译器和ISA决定
时钟周期（Cycle Time）和CPI主要由CPU的设计与实现决定

处理器设计过程

设计一个处理器的五个步骤：

1. 分析指令集以推导出数据通路的要求。
2. 选择一组数据通路组件并建立时钟方法。
3. 组装数据路径以迎合需求。
   1~3是数据通路的设计步骤
4. 分析每条指令的实现，以确定影响寄存器传输的控制点的设置。
5. 组装控制逻辑：制定逻辑方程并设计电路
   5~6是控制部件的设计步骤
   

MIPS 中的指令形式

MIPS：无内部互锁流水级的微处理器（Microprocessor without Interlocked Piped Stages）
具体关于MIPS的ISA可以点击传送门：MIPS指令集架构（需要魔法访问）

MIPS的特点：

• 本课程讨论的所有MIPS指令都是32-btis 长的。
• 格式少且字段固定
• 内存操作种类确定且单一
• 内存中操作数对齐，访存次数只有一次
• MIPS指令集是一种典型的RISC精简架构指令集

三个典型的MIPS指令形式如下。

一些典型的MIPS指令

我们先了解如何实现仅包含以下指令的简化 MIPS CPU

• Arithmetic-logical instructions: add, sub, and, or, slt
• Control flow instruction(s): beq
• Memory-reference instructions: lw, sw
• A subset of MIPS core ISA
  注意，上面所有的指令都要使用ALU

下面列出几个典型的指令

1. LW：将存储器的数据加载到寄存器堆。GPR表示CPU general-purpose register，也叫Register File。

2. SW：将寄存器堆里的一个数存到存储器中。

3. ADD：将两个存储在寄存器堆的数相加，结果存到寄存器堆。

4. ADDI：将寄存器堆中的一个数和立即数相加再存储到寄存器堆。
   
5. ADDI：将寄存器堆中的一个数和无符号立即数相加再存储到寄存器堆。
   
6. ADDU：寄存器堆中的两个无符号数相加，结果存到寄存器堆。
   
7. BEQ：两个寄存器堆里面的数相等即产生分支，分支指令地址偏移由offset指定
   

指令执行的基本步骤

1. Instruction Fetch：从指令地址获取指令，指令存储在存储器中。
2. Decode：解码指令后访问寄存器堆。
3. Execution：在ALU中执行指令的加法等算术和与或非等逻辑操作。
4. Memory Access：访问存储器，要么从存储器取数据，要么把数据存储在存储器里。
5. Write back results to registers：将数据写回寄存器堆。
6. 程序计数器PC（Program counter）移动到下一个指令地址。

初步连接数据通路部件的简易CPU

上图是初步的CPU数据通路图，下面我们将其切块细嚼。

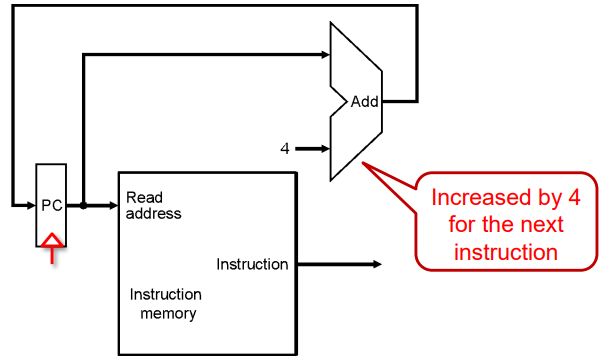
PC的数据通路

RTL级操作：

1. 获取指令: inst <- mem[PC]
2. 更新程序计数器：

• Sequential Code: PC <- PC + 4（+4是因为看成32位系统，地址按字节寻址）
• Branch and Jump: PC <- “something else”

寄存器堆的数据通路

示例: add rd, rs, rt
R[rd] <- R[rs] op R[rt]

通过rs和rt这两个地址索引从寄存器堆中获取要相加的数，将相加的结果送回rd所指向的寄存器堆中的地址。

Load操作的数据通路

示例: lw rt, rs, imm16
R[rt] <- Mem[R[rs] + SignExt[imm16]]

Store操作的数据通路

示例：sw rt, rs, imm16
Mem[R[rs] + SignExt[imm16]] <- R[rt]

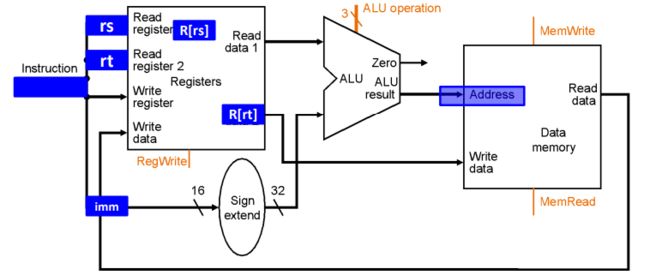
注意，Load和Store操作的立即数都是往存储器地址上加的

分支操作的数据通路

示例: beq rs, rt, imm16
Z <- (rs == rt); if Z, PC = PC+4+imm; else PC = PC+4

1. 读寄存器里面的操作数
2. 使用ALU中的减法操作比较两个操作数是否相等（减法结果为0即相等）
3. 计算目标地址：符号位扩展，移位，PC+4（+imm）

组装好的单周期处理器数据通路

注意这是单周期处理器，数据通路里面不包含寄存器，所有的指令都在一个时钟周期内完成。

设计单周期数据通路的控制器

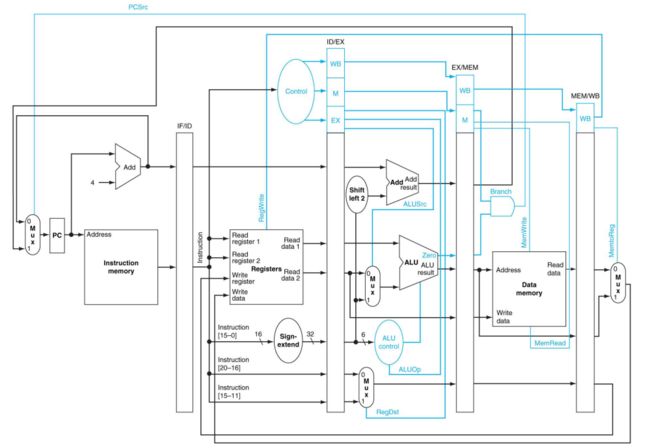
ALU控制

• 五个功能的ALU
  
• 基于指令的操作码（位 31-26）和功能码（位 5-0）进行解码

ALU控制的逻辑电路

CPU所有控制部件

橙色的线表示控制部件

控制部件+数据通路的单周期CPU原理图

下图是支持9条指令的单周期处理器 （add, sub, and, or, slt, lw, sw, beq, j）
这张图要能画出来

总结：处理器设计步骤

ISA确定后，进行处理器设计的大致步骤
第一步：分析每条指令的功能，并用RTL(Register Transfer Language)
来表示
第二步：根据指令的功能给出所需的元件，考虑时钟方案
第三步：将数据通路互连
第四步：确定每个元件所需控制信号的取值。汇总所有指令所涉及到的
控制信号，生成一张反映指令与控制信号之间关系的表
第五步：根据表得到每个控制信号的逻辑表达式，据此设计控制器电路

• 处理器设计涉及到数据通路的设计和控制器的设计
• 数据通路中有两种元件
  • 操作元件：由组合逻辑电路实现
  • 存储（状态）元件：由时序逻辑电路实现

多周期CPU

相较于单周期的好处：

1. 不同指令不同时间执行，没必要像多单周期一样非得按照最长指令的执行时间设置系统时钟。
2. 能够重用某些功能部件，如memory、ALU等等（使用pipeline）

• 每条指令分成多个阶段，每个阶段在一个时钟内完成
• 不同指令包含的时钟个数不同
• 阶段的划分要均衡，每个阶段只能完成一个独立、简单的功能，如：
一次ALU操作
一次存储器访问
一次寄存器存取
• 需加临时寄存器存放指令执行的中间结果
• 同一个功能部件能在不同的时钟中被重复使用
• 可用有限状态机来表示指令执行流程，并以此设计控制

单周期，多周期和流水线处理器的比较

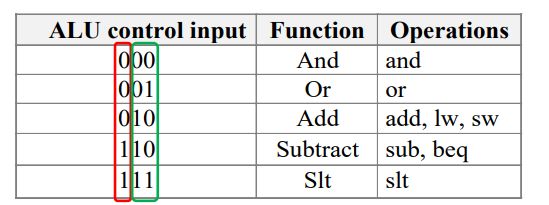
流水线 MIPS32 数据通路概览

带控制信号的流水线数据路径

流水线数据路径，具有用于处理冒险（hazards）和异常（exceptions）的控制措施

黄线框框表示处理冒险的部分，红色圆圈表示处理异常的部分。

异常(Exception)和中断(Interrupt)

°程序执行过程中CPU会遇到一些特殊情况，使正在执行的程序被“打断”
• 此时，CPU中止原来正在执行的程序，转到处理异常情况或特殊事件的程序去执行，执行后再返回到原被中止的程序处（断点）继续执行
° 程序执行被 “打断” 的事件有两类
• 内部“异常”：在CPU内部发生的意外事件或特殊事件
按发生原因分为硬故障中断和程序性中断两类
硬故障中断：如电源掉电、硬件线路故障等
程序性中断：执行某条指令时发生的“例外”，如算术溢出、缺页、越界、越权、非法指令、除数为0、堆栈溢出、访问超时、断点设置、单步、系统调用等
• 外部“中断”：在CPU外部发生的特殊事件
通过“中断请求”信号向CPU请求处理。如实时钟、控制台、打印机缺纸、外设准备好、采样计时到、DMA传输结束等
° 通常，异常指控制流中任何意外改变，中断特指来自外部事件
° 中断处理(Interrupt handling，或称中断服务程序)用来处理异常和中断
° CPU周而复始执行指令
• 执行指令过程中，若发现异常，则立即转异常处理（或作出检测标记，记录原因，并到指令最后阶段再处理）
• 每个指令结束，查询有没有中断请求，有则响应中

作业

问题1（Amdahl定律）

在实现一个应用程序的并行化时，理想加速比应当等于处理器的个数。但它受到两个因素的限制:可并行化的应用程序百分比和通信成本。Amdahl 定律考虑了前者，但没有考虑后者。

1. 如果应用程序的 80%可以并行化N个处理器的加速比为多少?(忽略通信成本）
2. 如果每增加一个处理器，通信开销为原执行时间的 0.5%，则8个处理器的加速比为多少?
3. 如果处理器数目每增加一倍，通信开销增加原执行时间的 0.5%，则8个处理器的加速比为多少?
4. 如果处理器数目每增加一倍，通信开销增加原执行时间的 0.5%，则N个处理器的加速比为多少?
5. 写出求解这一问题的一般公式:如果一个应用程序 P%的原执行时间可以并行化并且处理器数目每增加一倍，通信成本增加原执行时间的 0.5%，则达到最高加速比的处理器数目为多少?

解：
Amdahl定律$Speed\_up=\frac{origin\_time}{optimal\_time}=\frac{t}{t\times s+\frac{t\times p}{n}}=\frac{1}{s+\frac{p}{n}}$，其中s表示只能串行的比例，p表示并行的比例，n表示处理器个数。
修改版Amdal定律：$Speed\_up=\frac{origin\_time}{optimal\_time+communication\_time}=\frac{t}{t\times s+\frac{t\times p}{n}+t^{\prime }}=\frac{1}{s+\frac{p}{n}+t^{\prime }}$，公式中的$t^{\prime }$表示通信所用时间。

a. $\begin{array}{r}Speed\_up=\frac{1}{0.8+\frac{0.2}{N}}\end{array}$

b. $Speed\_up=\frac{1}{0.8+\frac{0.2}{8}+8\times 0.005}$

c.$Speed\_up=\frac{1}{0.8+\frac{0.2}{8}+({\log }_{2}8)\times 0.005}$

d. $Speed\_up=\frac{1}{0.8+\frac{0.2}{N}+({\log }_{2}N)\times 0.005}$

e.$Speed\_up=\frac{1}{(l-P\%)+\frac{P\%}{N}+({\log }_{2}N)\times 0.005}$，对此式求导令其等于0得最大值$N=2Pln2$

问题2（流水线、CPI、加速比）

我们首先考虑一个采用单周期实现的计算机。在按功能分制流水级时，这些流水级需要的时间不一定相同。原机器的时钟周期时间为 7 ns。在流水线被分之后，测得的时间数据为:IF，1ns; ID，1.5s; EX，1ns; MEM，2ns; WB，1.5ns。流水线寄存器延迟为0.1ns。
a.5 级流水化机器的时钟周期时间为多少?
b.如果每4条指令有一次停顿，则新机器的 CPI为多少?
c.流水化机器相对于单周期机器的加速比为多少?
d.如果流水化机器有无限个流水级，那它相对于单周期机器的加速比为多少?

解：
我们假定流水线的CPI=1.
a. 找最大延迟时间的阶段为MEM，所以周期为2+0.1=2.1ns。
b.CPI为每条指令平均所花费的时钟周期数。这道题我们假设流水线已经流起来了，也即每个周期都能执行一条指令。所以$CPI=\frac{5}{4}=1.25$

c. $Speed\_up=\frac{(IC\times CPI\times cycle\_time{)}_{single}}{(IC\times CPI\times cycle\_time{)}_{mulii}}=\frac{7}{1.25\times 2.1}=2.67$

d. $Speed\_up=\frac{(IC\times CPI\times cycle\_time{)}_{single}}{(IC\times CPI\times cycle\_time{)}_{multi}}=\frac{7}{0.1}=70$

以上就是本篇博文，下一篇我们来讲复杂CPU流水线与乱序执行