【数模百科】一篇文章讲清楚遗传算法
本篇文章摘录自 遗传算法 - 数模百科,如果你想了解更多有关智能优化算法的信息,请移步 智能优化算法 - 数模百科
白话文
遗传算法的灵感来源非常自然,就是大自然里的生物进化过程。在自然界中,生物为了更好地适应环境,会不断进化。这个过程中,最适应环境的生物能生存下来,繁衍后代,而那些不适应环境的生物则会逐渐被淘汰。生物的这一进化过程就是遗传算法的核心思想。
那么,为什么人们要发明这样一个算法呢?问题是这样的,现实世界中有很多复杂的问题,比如说设计一架飞机,或者是安排一个生产线上的工作流程,这些问题往往非常复杂,有很多变量和限制条件,用传统的数学方法求解起来非常困难,甚至有的问题根本就没有固定的公式可以套用。这时候,科学家们就想,既然大自然的进化能找到生物适应环境的解决方案,那我们是不是可以模仿这个过程,来解决这些复杂的问题呢?
所以,遗传算法就是这样产生的。它用一种模拟自然界中生物遗传和进化的方法,来逐步寻找问题的解决方案。这个算法不需要一个固定的公式,而是通过一种类似自然选择的方式,不断迭代,逐步淘汰掉那些不好的解决方案,保留并优化那些好的方案,最终找到一个足够好的答案。
遗传算法特别适合于那些复杂的、传统算法难以解决的问题。比如优化问题,我们可能要在成百上千的可能性中找到最好的那一个,比如说路线规划、工业设计、财务预测等等。在这些场景下,遗传算法就像是一个智能的试错者,它不断尝试,然后从中学习,不断进化,直到找到一个足够好的解决方案。
总之,遗传算法就是借鉴了大自然的智慧,通过模拟生物的遗传和进化过程,来帮助我们解决那些头疼的复杂问题。它的优势在于能够在众多可能的解决方案中,找到相对优秀的答案,而不需要预先给出一个固定的解决路径。
举个例子。
你要组织一个周末郊游,目标是找到最满意的行程计划。
首先,你可以列出一些可能的行程方案,这些方案就像是遗传算法中的"初始种群"。每个方案都包含了行程的各个细节,比如去哪些地方、在哪里吃饭、怎样安排时间等等。
接着,你需要一个评价标准,比如成本、乐趣、时间等,这些就像是自然选择中的“适应性”。你会根据这些标准来评估哪些行程计划更好,哪些不太理想。
然后,就像遗传算法中的“遗传”过程,你可能会从不同的行程方案中抽取你喜欢的部分,组合成一个新的行程方案。比如,你喜欢方案A的目的地,喜欢方案B的餐厅选择,于是就把这两部分结合起来,形成一个新的方案。
过程中,你也会做一些随机的尝试,比如突发奇想想去一个之前没有考虑过的地方,这就像是遗传算法中的“变异”。
经过几轮这样的筛选、组合和变异,你最终会筛选出一个你认为最满意的行程计划。这整个过程,其实就是遗传算法在生活中的一个简化版应用,帮助你从众多的可能性中找到一个最佳的选择。
定义与详解
定义与解法
遗传算法是一种模仿生物界中自然选择和基因遗传机制的智能搜索算法。它通过模拟自然进化过程来寻找问题的最优解。接下来,我将用简单易懂的语言,详细解释遗传算法的每一步。
首先是编码。在遗传算法中,我们通常会把要解决问题的答案表示成一串特定的代码,这就像是生物的DNA一样。我们最常用的编码方式是二进制编码,也就是用0和1的组合来表示一个解。
接下来是初始种群的设定。我们随机生成一组个体,这些个体就构成了我们算法的起始点。每个个体都是问题的一个可能解,它们是通过上面提到的编码方式来表示的。
然后,我们需要设定一个适应度函数。这个函数的作用是判断每个解的好坏,就像自然界中适者生存一样。它能告诉我们哪些个体适应环境,哪些不适应。
有了这些基础后,我们就开始迭代过程:
选择:这一步我们会根据每个个体的适应度来选择。就像自然界中动物繁衍后代一样,适应度高的个体被选择的机会更大。我们常用一种叫做“轮盘赌”的方法来随机选择,确保那些适应度高的个体更容易被选中。
交叉:这一步模拟的是生物的交配过程。我们会随机挑选两个个体,然后将它们的编码按照一定规则进行组合,产生新的个体。这个步骤相当于是产生了后代。
变异:在自然界中,变异可以增加种群的多样性。在遗传算法中,我们也会以很小的概率随机改变个体中的某个基因,这样做可以防止算法停滞不前,只在局部最优解中徘徊。
最后是解码。当我们通过遗传算法得到了一组优秀的编码串后,我们需要将它们转换回实际问题的答案。
整个过程会不断重复,直到达到某个停止条件,比如达到了最大迭代次数,或者找到了满意的答案。最后,我们从种群中选出适应度最高的个体,将其解码,得到我们的最优解。
举个例子来说,如果我们要用遗传算法来解决旅行商问题(即找到一条访问每个城市一次且总距离最短的路线),那么:
-
编码可能是一个表示城市访问顺序的数字序列。
-
初始种群可能是随机生成的几个不同的访问序列。
-
适应度函数可能是计算旅行总距离的函数,总距离越短,适应度越高。
-
选择就是基于路径的总距离来进行,越短的路径被选择的概率越大。
-
交叉可以通过将两条路径的一部分拼接起来的方式来产生新的路径。
-
变异可能是随机交换路径中两个城市的顺序。
-
解码就是将数字序列转换回实际的城市访问路径。
通过这样的迭代过程,我们就能逐渐找到旅行总距离最短的路径。
轮盘法
轮盘赌选择法(Roulette Wheel Selection)是遗传算法中用于选择优秀个体以进行下一代繁衍的一种策略。这种方法的设计初衷是模拟自然选择的过程,即适者生存,适应环境的个体有更高的机会繁衍后代。下面我将尽量以简单易懂的方式详细解释轮盘赌选择法。
-
对种群中的每个个体计算适应度。 首先,我们需要给种群中的每一个个体都计算一个适应度值,这个值反映了个体对环境的适应程度。适应度高的个体更有可能被选中繁衍后代。
-
累加所有个体的适应度,得到总适应度。 接着,我们将所有个体的适应度值加起来,得到种群的总适应度。
-
计算相对适应度。为每个个体分配一个选择概率,即个体适应度与总适应度的比值,。其数学表示为:
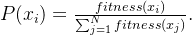
这里,
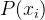 表示个体
表示个体  被选中的概率,
被选中的概率,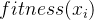 是个体
是个体  的适应度值,
的适应度值, 是种群中所有个体适应度的总和。
是种群中所有个体适应度的总和。 -
选择个体:最后,我们通过生成一个0-1之间的随机数来模拟轮盘赌转动的过程。根据这个随机数落在的区间,我们可以确定哪个个体被选中。每个个体的选择区间大小正比于其相对适应度。
-
根据随机数确定选中的个体。
轮盘赌选择法的优点:轮盘赌选择法由于是概率选择,能够保持种群的多样性,减少早熟收敛的可能性。这种方法在很多优化问题中特别有用,因为它可以帮助遗传算法探索更广阔的解空间,而不是仅仅局限在局部最优解附近。
伪代码如下:
程序 遗传算法
初始化种群 P(0)
计算种群 P(0) 中每个个体的适应度值
对于 t=1 到 最大代数
对于种群 P(t-1) 中的每个个体执行以下操作:
根据轮盘赌选择法选择个体
对选择出的个体进行交叉操作生成新的种群 C(t)
对种群 C(t) 中的个体执行变异操作
计算种群 C(t) 中每个个体的适应度值
将种群 C(t) 作为新的种群 P(t)
结束对于循环
结束程序进一步解释这段伪代码:
-
初始化种群 P(0):创建初始种群,也就是第0代的个体集合。 -
计算种群 P(0) 中每个个体的适应度值:评估初始种群中每个个体的适应度。 -
对于 t=1 到 最大代数:设置一个循环,从第1代开始迭代,直到达到预定的最大代数。 -
根据轮盘赌选择法选择个体:在当前种群中使用轮盘赌选择法选择个体,以便进行后续的繁殖操作。 -
对选择出的个体进行交叉操作生成新的种群 C(t):通过交叉操作(染色体交换)在选中的个体之间产生后代,形成新的种群。 -
对种群 C(t) 中的个体执行变异操作:对新生成的后代进行随机变异,以增加种群的多样性。 -
计算种群 C(t) 中每个个体的适应度值:评估经过交叉和变异后的种群的适应度。 -
将种群 C(t) 作为新的种群 P(t):新产生的种群成为下一代种群。 -
结束对于循环:重复上述步骤,直到达到最大代数或其他终止条件。 -
结束程序:算法结束,通常此时我们会输出找到的最优解或者种群中的最佳个体。
代码
import array
from deap import creator, base, tools, algorithms
import random
import numpy as np
# 建立10个城市的坐标
city_num = 10
cities = {
i: (random.randint(0, 100), random.randint(0, 100))
for i in range(city_num)
}
# 计算城市间距离
def dist(city1, city2):
return np.sqrt((cities[city1][0]-cities[city2][0])**2 + (cities[city1][1]-cities[city2][1])**2)
dist_matrix = [
[dist(city1, city2) for city2 in range(city_num)]
for city1 in range(city_num)
]
# 定义目标函数,即所有城市之间的距离总和
def total_dist(individual):
distance = dist_matrix[individual[-1]][individual[0]]
for gene1, gene2 in zip(individual[0:-1], individual[1:]):
distance += dist_matrix[gene1][gene2]
return distance,
# 适应度策略,采用最小化策略 Min
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
# 创建 Individual 类
creator.create("Individual", array.array, typecode='i', fitness=creator.FitnessMin)
toolbox = base.Toolbox()
# 定义产生染色体的函数,生成 0 到城市数目-1组成的随机序列
toolbox.register("indices", random.sample, range(city_num), city_num)
# 生成Individual类染色体的方法attribute
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.indices)
# 生成特定类群体的方法population
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# 定义个体适应度评价方法,计算旅行商路径长度
toolbox.register("evaluate", total_dist)
toolbox.register("mate", tools.cxOrdered)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.2)
toolbox.register("select", tools.selTournament, tournsize=3)
population = toolbox.population(n=100)
result, log = algorithms.eaSimple(population, toolbox, cxpb=0.7, mutpb=0.2, ngen=500, verbose=False)
best_individual = tools.selBest(population, k=1)[0]
print('最短距离:', total_dist(best_individual)[0])
print('最佳路径:', best_individual)这个代码定义了个体类型为代表城市排列的一维数组,适应度函数为求解所有城市间距离的函数。
然后定义了生成初始解、交叉变异等基本操作,使用之前定义的距离函数作为适应度评价函数。
接着设置好所需要的参数后开始调用经典的eaSimple算法进行求解(步骤与“定义与详解”中的步骤相同)。算法将历代的最优解放入hof变量中,我们在最后可以从中取出。
上述代码通过遗传算法寻找在城市间距离固定的情况下,使得总距离最短的旅行路径。
输出结果:
最短距离: 296.24988202042806
最佳路径: Individual('i', [6, 4, 3, 7, 5, 1, 0, 2, 8, 9])优缺点
优点:
-
全局搜索性能:遗传算法通过种群的进化和遗传操作,能够在解空间中进行全局搜索,避免陷入局部最优解。
-
适应性和灵活性:遗传算法具有一定的适应性和灵活性,能够针对不同问题进行调整和适应。
-
并行计算:遗传算法可以很好地进行并行计算,通过多个计算节点并行执行,提高求解效率。
-
能处理高维度问题:遗传算法相对适用于高维度的优化问题,不受维度限制。
缺点:
-
参数选择:遗传算法中的参数选择对其性能和结果有很大影响,需要进行合适的参数调优。
-
求解时间:遗传算法相对较慢,尤其在迭代次数较多、解空间复杂的情况下。
-
可能存在近似解:遗传算法可能找到接近最优解但不是最优解的结果,涉及一定的误差和近似性。
本文摘录自 数模百科 —— 遗传算法 - 数模百科
数模百科是一个由一群数模爱好者搭建的数学建模知识平台。我们想让大家只通过一个网站,就能解决自己在数学建模上的难题,把搜索和筛选的时间节省下来,投入到真正的学习当中。
我们团队目前正在努力为大家创建最好的信息集合,从用最简单易懂的话语和生动形象的例子帮助大家理解模型,到用科学严谨的语言讲解模型原理,再到提供参考代码。我们努力为数学建模的学习者和参赛者提供一站式学习平台,目前网站已上线,期待大家的反馈。
如果你想和我们的团队成员进行更深入的学习和交流,你可以通过公众号数模百科找到我们,我们会在这里发布更多资讯,也欢迎你来找我们唠嗑。