智能合约(改进版)
kmc.sol改进(1+2+3)
pragma solidity ^0.5.0;
import "verify.sol";
import "ARC.sol";
contract KMC{
ARC arc;
CVC cvc;
RVC rvc;
mapping(bytes32 => bytes32) public claims;
mapping(bytes32 => bytes32) public adjunction;
event LogTokenClaim(address indexed sender, bytes32 indexed tokenId, bytes32 indexed idClaim);
event LogTokenResponse(address indexed sender, bytes32 indexed tokenId, string res);
function setcliam(address c)public{
cvc = CVC(c);
}
function setarc(address a)public{
arc = ARC(a);
}
function setres(address r)public{
rvc = RVC(r);
}
function tokenClaim(uint[2] memory a, uint[2][2] memory b, uint[2] memory c, uint[5] memory input)public returns (bool){
//bytes32 id = packToBytes32(input[0],input[1]);
//bytes32 id = 0x2123e10a5c7a9e5bb3de5a568cb3a36f12ee705b47e47d109cdfcaf3b56faf21;
//bytes32 id_claim = 0x36f12ee705b47e47d109cdfcaf3b56faf212123e10a5c7a9e5bb3de5a568cb3a;
bytes32 id_claim = packToBytes32(input[2],input[3]);
bytes32 id = packToBytes32(input[0],input[1]);
bool reslut = cvc.claimPKVerify(a,b,c,input, msg.sender);
require (reslut == true, "verify failed!");
require (arc.creatorQuery(id) == msg.sender, "you are not the creator of token");
require (arc.claimedQuery(id) == false, "this token has been claimed");
require (arc.exisitQuery(id) == true, "this token has been revocationed!");
claims[id_claim] = id_claim;
arc.changeStatus(id);
emit LogTokenClaim(msg.sender, id, id_claim);
return true;
}
function tokenResponse(uint[2] memory a, uint[2][2] memory b, uint[2] memory c, uint[7] memory input, string memory res) public returns (bool){
bytes32 id = packToBytes32(input[0],input[1]);
bytes32 id_claim = packToBytes32(input[2],input[3]);
bytes32 id_ne = packToBytes32(input[4],input[5]);
// 将交易发送者的地址作为匿名地址,将其hash后的值作为adjunction映射的key
bytes32 senderHash = keccak256(abi.encodePacked(msg.sender));
require (adjunction[senderHash] == 0, "proof has been used!");
bool reslut = rvc.responseSKVerify(a,b,c,input, msg.sender);
require (reslut == true, "verify failed!");
require (arc.exisitQuery(id) == true, "this token has been revocationed!");
require (claims[id_claim] == id_claim, "this token has not beenclaimed");
// 将proof的值作为映射的value,并在执行完验证后,将adjunction映射中的key与相应的value绑定
adjunction[senderHash] = id_ne;
emit LogTokenResponse(msg.sender,id, res);
return true;
}
//function addclaim(bytes32 id_claim)public returns(uint){
// claims[id_claim] = id_claim;
//}
function packToBytes32(uint256 high, uint256 low)public pure returns (bytes32){
return bytes32(low) | (bytes32(high)<<128);
}
}verify.sol
// This file is LGPL3 Licensed
/**
* @title Elliptic curve operations on twist points for alt_bn128
* @author Mustafa Al-Bassam ([email protected])
* @dev Homepage: https://github.com/musalbas/solidity-BN256G2
*/
library BN256G2 {
uint256 internal constant FIELD_MODULUS = 0x30644e72e131a029b85045b68181585d97816a916871ca8d3c208c16d87cfd47;
uint256 internal constant TWISTBX = 0x2b149d40ceb8aaae81be18991be06ac3b5b4c5e559dbefa33267e6dc24a138e5;
uint256 internal constant TWISTBY = 0x9713b03af0fed4cd2cafadeed8fdf4a74fa084e52d1852e4a2bd0685c315d2;
uint internal constant PTXX = 0;
uint internal constant PTXY = 1;
uint internal constant PTYX = 2;
uint internal constant PTYY = 3;
uint internal constant PTZX = 4;
uint internal constant PTZY = 5;
/**
* @notice Add two twist points
* @param pt1xx Coefficient 1 of x on point 1
* @param pt1xy Coefficient 2 of x on point 1
* @param pt1yx Coefficient 1 of y on point 1
* @param pt1yy Coefficient 2 of y on point 1
* @param pt2xx Coefficient 1 of x on point 2
* @param pt2xy Coefficient 2 of x on point 2
* @param pt2yx Coefficient 1 of y on point 2
* @param pt2yy Coefficient 2 of y on point 2
* @return (pt3xx, pt3xy, pt3yx, pt3yy)
*/
function ECTwistAdd(
uint256 pt1xx, uint256 pt1xy,
uint256 pt1yx, uint256 pt1yy,
uint256 pt2xx, uint256 pt2xy,
uint256 pt2yx, uint256 pt2yy
) public view returns (
uint256, uint256,
uint256, uint256
) {
if (
pt1xx == 0 && pt1xy == 0 &&
pt1yx == 0 && pt1yy == 0
) {
if (!(
pt2xx == 0 && pt2xy == 0 &&
pt2yx == 0 && pt2yy == 0
)) {
assert(_isOnCurve(
pt2xx, pt2xy,
pt2yx, pt2yy
));
}
return (
pt2xx, pt2xy,
pt2yx, pt2yy
);
} else if (
pt2xx == 0 && pt2xy == 0 &&
pt2yx == 0 && pt2yy == 0
) {
assert(_isOnCurve(
pt1xx, pt1xy,
pt1yx, pt1yy
));
return (
pt1xx, pt1xy,
pt1yx, pt1yy
);
}
assert(_isOnCurve(
pt1xx, pt1xy,
pt1yx, pt1yy
));
assert(_isOnCurve(
pt2xx, pt2xy,
pt2yx, pt2yy
));
uint256[6] memory pt3 = _ECTwistAddJacobian(
pt1xx, pt1xy,
pt1yx, pt1yy,
1, 0,
pt2xx, pt2xy,
pt2yx, pt2yy,
1, 0
);
return _fromJacobian(
pt3[PTXX], pt3[PTXY],
pt3[PTYX], pt3[PTYY],
pt3[PTZX], pt3[PTZY]
);
}
/**
* @notice Multiply a twist point by a scalar
* @param s Scalar to multiply by
* @param pt1xx Coefficient 1 of x
* @param pt1xy Coefficient 2 of x
* @param pt1yx Coefficient 1 of y
* @param pt1yy Coefficient 2 of y
* @return (pt2xx, pt2xy, pt2yx, pt2yy)
*/
function ECTwistMul(
uint256 s,
uint256 pt1xx, uint256 pt1xy,
uint256 pt1yx, uint256 pt1yy
) public view returns (
uint256, uint256,
uint256, uint256
) {
uint256 pt1zx = 1;
if (
pt1xx == 0 && pt1xy == 0 &&
pt1yx == 0 && pt1yy == 0
) {
pt1xx = 1;
pt1yx = 1;
pt1zx = 0;
} else {
assert(_isOnCurve(
pt1xx, pt1xy,
pt1yx, pt1yy
));
}
uint256[6] memory pt2 = _ECTwistMulJacobian(
s,
pt1xx, pt1xy,
pt1yx, pt1yy,
pt1zx, 0
);
return _fromJacobian(
pt2[PTXX], pt2[PTXY],
pt2[PTYX], pt2[PTYY],
pt2[PTZX], pt2[PTZY]
);
}
/**
* @notice Get the field modulus
* @return The field modulus
*/
function GetFieldModulus() public pure returns (uint256) {
return FIELD_MODULUS;
}
function submod(uint256 a, uint256 b, uint256 n) internal pure returns (uint256) {
return addmod(a, n - b, n);
}
function _FQ2Mul(
uint256 xx, uint256 xy,
uint256 yx, uint256 yy
) internal pure returns (uint256, uint256) {
return (
submod(mulmod(xx, yx, FIELD_MODULUS), mulmod(xy, yy, FIELD_MODULUS), FIELD_MODULUS),
addmod(mulmod(xx, yy, FIELD_MODULUS), mulmod(xy, yx, FIELD_MODULUS), FIELD_MODULUS)
);
}
function _FQ2Muc(
uint256 xx, uint256 xy,
uint256 c
) internal pure returns (uint256, uint256) {
return (
mulmod(xx, c, FIELD_MODULUS),
mulmod(xy, c, FIELD_MODULUS)
);
}
function _FQ2Add(
uint256 xx, uint256 xy,
uint256 yx, uint256 yy
) internal pure returns (uint256, uint256) {
return (
addmod(xx, yx, FIELD_MODULUS),
addmod(xy, yy, FIELD_MODULUS)
);
}
function _FQ2Sub(
uint256 xx, uint256 xy,
uint256 yx, uint256 yy
) internal pure returns (uint256 rx, uint256 ry) {
return (
submod(xx, yx, FIELD_MODULUS),
submod(xy, yy, FIELD_MODULUS)
);
}
function _FQ2Div(
uint256 xx, uint256 xy,
uint256 yx, uint256 yy
) internal view returns (uint256, uint256) {
(yx, yy) = _FQ2Inv(yx, yy);
return _FQ2Mul(xx, xy, yx, yy);
}
function _FQ2Inv(uint256 x, uint256 y) internal view returns (uint256, uint256) {
uint256 inv = _modInv(addmod(mulmod(y, y, FIELD_MODULUS), mulmod(x, x, FIELD_MODULUS), FIELD_MODULUS), FIELD_MODULUS);
return (
mulmod(x, inv, FIELD_MODULUS),
FIELD_MODULUS - mulmod(y, inv, FIELD_MODULUS)
);
}
function _isOnCurve(
uint256 xx, uint256 xy,
uint256 yx, uint256 yy
) internal pure returns (bool) {
uint256 yyx;
uint256 yyy;
uint256 xxxx;
uint256 xxxy;
(yyx, yyy) = _FQ2Mul(yx, yy, yx, yy);
(xxxx, xxxy) = _FQ2Mul(xx, xy, xx, xy);
(xxxx, xxxy) = _FQ2Mul(xxxx, xxxy, xx, xy);
(yyx, yyy) = _FQ2Sub(yyx, yyy, xxxx, xxxy);
(yyx, yyy) = _FQ2Sub(yyx, yyy, TWISTBX, TWISTBY);
return yyx == 0 && yyy == 0;
}
function _modInv(uint256 a, uint256 n) internal view returns (uint256 result) {
bool success;
assembly {
let freemem := mload(0x40)
mstore(freemem, 0x20)
mstore(add(freemem,0x20), 0x20)
mstore(add(freemem,0x40), 0x20)
mstore(add(freemem,0x60), a)
mstore(add(freemem,0x80), sub(n, 2))
mstore(add(freemem,0xA0), n)
success := staticcall(sub(gas, 2000), 5, freemem, 0xC0, freemem, 0x20)
result := mload(freemem)
}
require(success);
}
function _fromJacobian(
uint256 pt1xx, uint256 pt1xy,
uint256 pt1yx, uint256 pt1yy,
uint256 pt1zx, uint256 pt1zy
) internal view returns (
uint256 pt2xx, uint256 pt2xy,
uint256 pt2yx, uint256 pt2yy
) {
uint256 invzx;
uint256 invzy;
(invzx, invzy) = _FQ2Inv(pt1zx, pt1zy);
(pt2xx, pt2xy) = _FQ2Mul(pt1xx, pt1xy, invzx, invzy);
(pt2yx, pt2yy) = _FQ2Mul(pt1yx, pt1yy, invzx, invzy);
}
function _ECTwistAddJacobian(
uint256 pt1xx, uint256 pt1xy,
uint256 pt1yx, uint256 pt1yy,
uint256 pt1zx, uint256 pt1zy,
uint256 pt2xx, uint256 pt2xy,
uint256 pt2yx, uint256 pt2yy,
uint256 pt2zx, uint256 pt2zy) internal pure returns (uint256[6] memory pt3) {
if (pt1zx == 0 && pt1zy == 0) {
(
pt3[PTXX], pt3[PTXY],
pt3[PTYX], pt3[PTYY],
pt3[PTZX], pt3[PTZY]
) = (
pt2xx, pt2xy,
pt2yx, pt2yy,
pt2zx, pt2zy
);
return pt3;
} else if (pt2zx == 0 && pt2zy == 0) {
(
pt3[PTXX], pt3[PTXY],
pt3[PTYX], pt3[PTYY],
pt3[PTZX], pt3[PTZY]
) = (
pt1xx, pt1xy,
pt1yx, pt1yy,
pt1zx, pt1zy
);
return pt3;
}
(pt2yx, pt2yy) = _FQ2Mul(pt2yx, pt2yy, pt1zx, pt1zy); // U1 = y2 * z1
(pt3[PTYX], pt3[PTYY]) = _FQ2Mul(pt1yx, pt1yy, pt2zx, pt2zy); // U2 = y1 * z2
(pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1zx, pt1zy); // V1 = x2 * z1
(pt3[PTZX], pt3[PTZY]) = _FQ2Mul(pt1xx, pt1xy, pt2zx, pt2zy); // V2 = x1 * z2
if (pt2xx == pt3[PTZX] && pt2xy == pt3[PTZY]) {
if (pt2yx == pt3[PTYX] && pt2yy == pt3[PTYY]) {
(
pt3[PTXX], pt3[PTXY],
pt3[PTYX], pt3[PTYY],
pt3[PTZX], pt3[PTZY]
) = _ECTwistDoubleJacobian(pt1xx, pt1xy, pt1yx, pt1yy, pt1zx, pt1zy);
return pt3;
}
(
pt3[PTXX], pt3[PTXY],
pt3[PTYX], pt3[PTYY],
pt3[PTZX], pt3[PTZY]
) = (
1, 0,
1, 0,
0, 0
);
return pt3;
}
(pt2zx, pt2zy) = _FQ2Mul(pt1zx, pt1zy, pt2zx, pt2zy); // W = z1 * z2
(pt1xx, pt1xy) = _FQ2Sub(pt2yx, pt2yy, pt3[PTYX], pt3[PTYY]); // U = U1 - U2
(pt1yx, pt1yy) = _FQ2Sub(pt2xx, pt2xy, pt3[PTZX], pt3[PTZY]); // V = V1 - V2
(pt1zx, pt1zy) = _FQ2Mul(pt1yx, pt1yy, pt1yx, pt1yy); // V_squared = V * V
(pt2yx, pt2yy) = _FQ2Mul(pt1zx, pt1zy, pt3[PTZX], pt3[PTZY]); // V_squared_times_V2 = V_squared * V2
(pt1zx, pt1zy) = _FQ2Mul(pt1zx, pt1zy, pt1yx, pt1yy); // V_cubed = V * V_squared
(pt3[PTZX], pt3[PTZY]) = _FQ2Mul(pt1zx, pt1zy, pt2zx, pt2zy); // newz = V_cubed * W
(pt2xx, pt2xy) = _FQ2Mul(pt1xx, pt1xy, pt1xx, pt1xy); // U * U
(pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt2zx, pt2zy); // U * U * W
(pt2xx, pt2xy) = _FQ2Sub(pt2xx, pt2xy, pt1zx, pt1zy); // U * U * W - V_cubed
(pt2zx, pt2zy) = _FQ2Muc(pt2yx, pt2yy, 2); // 2 * V_squared_times_V2
(pt2xx, pt2xy) = _FQ2Sub(pt2xx, pt2xy, pt2zx, pt2zy); // A = U * U * W - V_cubed - 2 * V_squared_times_V2
(pt3[PTXX], pt3[PTXY]) = _FQ2Mul(pt1yx, pt1yy, pt2xx, pt2xy); // newx = V * A
(pt1yx, pt1yy) = _FQ2Sub(pt2yx, pt2yy, pt2xx, pt2xy); // V_squared_times_V2 - A
(pt1yx, pt1yy) = _FQ2Mul(pt1xx, pt1xy, pt1yx, pt1yy); // U * (V_squared_times_V2 - A)
(pt1xx, pt1xy) = _FQ2Mul(pt1zx, pt1zy, pt3[PTYX], pt3[PTYY]); // V_cubed * U2
(pt3[PTYX], pt3[PTYY]) = _FQ2Sub(pt1yx, pt1yy, pt1xx, pt1xy); // newy = U * (V_squared_times_V2 - A) - V_cubed * U2
}
function _ECTwistDoubleJacobian(
uint256 pt1xx, uint256 pt1xy,
uint256 pt1yx, uint256 pt1yy,
uint256 pt1zx, uint256 pt1zy
) internal pure returns (
uint256 pt2xx, uint256 pt2xy,
uint256 pt2yx, uint256 pt2yy,
uint256 pt2zx, uint256 pt2zy
) {
(pt2xx, pt2xy) = _FQ2Muc(pt1xx, pt1xy, 3); // 3 * x
(pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1xx, pt1xy); // W = 3 * x * x
(pt1zx, pt1zy) = _FQ2Mul(pt1yx, pt1yy, pt1zx, pt1zy); // S = y * z
(pt2yx, pt2yy) = _FQ2Mul(pt1xx, pt1xy, pt1yx, pt1yy); // x * y
(pt2yx, pt2yy) = _FQ2Mul(pt2yx, pt2yy, pt1zx, pt1zy); // B = x * y * S
(pt1xx, pt1xy) = _FQ2Mul(pt2xx, pt2xy, pt2xx, pt2xy); // W * W
(pt2zx, pt2zy) = _FQ2Muc(pt2yx, pt2yy, 8); // 8 * B
(pt1xx, pt1xy) = _FQ2Sub(pt1xx, pt1xy, pt2zx, pt2zy); // H = W * W - 8 * B
(pt2zx, pt2zy) = _FQ2Mul(pt1zx, pt1zy, pt1zx, pt1zy); // S_squared = S * S
(pt2yx, pt2yy) = _FQ2Muc(pt2yx, pt2yy, 4); // 4 * B
(pt2yx, pt2yy) = _FQ2Sub(pt2yx, pt2yy, pt1xx, pt1xy); // 4 * B - H
(pt2yx, pt2yy) = _FQ2Mul(pt2yx, pt2yy, pt2xx, pt2xy); // W * (4 * B - H)
(pt2xx, pt2xy) = _FQ2Muc(pt1yx, pt1yy, 8); // 8 * y
(pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1yx, pt1yy); // 8 * y * y
(pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt2zx, pt2zy); // 8 * y * y * S_squared
(pt2yx, pt2yy) = _FQ2Sub(pt2yx, pt2yy, pt2xx, pt2xy); // newy = W * (4 * B - H) - 8 * y * y * S_squared
(pt2xx, pt2xy) = _FQ2Muc(pt1xx, pt1xy, 2); // 2 * H
(pt2xx, pt2xy) = _FQ2Mul(pt2xx, pt2xy, pt1zx, pt1zy); // newx = 2 * H * S
(pt2zx, pt2zy) = _FQ2Mul(pt1zx, pt1zy, pt2zx, pt2zy); // S * S_squared
(pt2zx, pt2zy) = _FQ2Muc(pt2zx, pt2zy, 8); // newz = 8 * S * S_squared
}
function _ECTwistMulJacobian(
uint256 d,
uint256 pt1xx, uint256 pt1xy,
uint256 pt1yx, uint256 pt1yy,
uint256 pt1zx, uint256 pt1zy
) internal pure returns (uint256[6] memory pt2) {
while (d != 0) {
if ((d & 1) != 0) {
pt2 = _ECTwistAddJacobian(
pt2[PTXX], pt2[PTXY],
pt2[PTYX], pt2[PTYY],
pt2[PTZX], pt2[PTZY],
pt1xx, pt1xy,
pt1yx, pt1yy,
pt1zx, pt1zy);
}
(
pt1xx, pt1xy,
pt1yx, pt1yy,
pt1zx, pt1zy
) = _ECTwistDoubleJacobian(
pt1xx, pt1xy,
pt1yx, pt1yy,
pt1zx, pt1zy
);
d = d / 2;
}
}
}
// This file is MIT Licensed.
//
// Copyright 2017 Christian Reitwiessner
// Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
// The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
// THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
pragma solidity ^0.5.0;
library Pairing {
struct G1Point {
uint X;
uint Y;
}
// Encoding of field elements is: X[0] * z + X[1]
struct G2Point {
uint[2] X;
uint[2] Y;
}
/// @return the generator of G1
function P1() pure internal returns (G1Point memory) {
return G1Point(1, 2);
}
/// @return the generator of G2
function P2() pure internal returns (G2Point memory) {
return G2Point(
[11559732032986387107991004021392285783925812861821192530917403151452391805634,
10857046999023057135944570762232829481370756359578518086990519993285655852781],
[4082367875863433681332203403145435568316851327593401208105741076214120093531,
8495653923123431417604973247489272438418190587263600148770280649306958101930]
);
}
/// @return the negation of p, i.e. p.addition(p.negate()) should be zero.
function negate(G1Point memory p) pure internal returns (G1Point memory) {
// The prime q in the base field F_q for G1
uint q = 21888242871839275222246405745257275088696311157297823662689037894645226208583;
if (p.X == 0 && p.Y == 0)
return G1Point(0, 0);
return G1Point(p.X, q - (p.Y % q));
}
/// @return the sum of two points of G1
function addition(G1Point memory p1, G1Point memory p2) internal returns (G1Point memory r) {
uint[4] memory input;
input[0] = p1.X;
input[1] = p1.Y;
input[2] = p2.X;
input[3] = p2.Y;
bool success;
assembly {
success := call(sub(gas, 2000), 6, 0, input, 0xc0, r, 0x60)
// Use "invalid" to make gas estimation work
switch success case 0 { invalid() }
}
require(success);
}
/// @return the sum of two points of G2
function addition(G2Point memory p1, G2Point memory p2) internal view returns (G2Point memory r) {
(r.X[1], r.X[0], r.Y[1], r.Y[0]) = BN256G2.ECTwistAdd(p1.X[1],p1.X[0],p1.Y[1],p1.Y[0],p2.X[1],p2.X[0],p2.Y[1],p2.Y[0]);
}
/// @return the product of a point on G1 and a scalar, i.e.
/// p == p.scalar_mul(1) and p.addition(p) == p.scalar_mul(2) for all points p.
function scalar_mul(G1Point memory p, uint s) internal returns (G1Point memory r) {
uint[3] memory input;
input[0] = p.X;
input[1] = p.Y;
input[2] = s;
bool success;
assembly {
success := call(sub(gas, 2000), 7, 0, input, 0x80, r, 0x60)
// Use "invalid" to make gas estimation work
switch success case 0 { invalid() }
}
require (success);
}
/// @return the result of computing the pairing check
/// e(p1[0], p2[0]) * .... * e(p1[n], p2[n]) == 1
/// For example pairing([P1(), P1().negate()], [P2(), P2()]) should
/// return true.
function pairing(G1Point[] memory p1, G2Point[] memory p2) internal returns (bool) {
require(p1.length == p2.length);
uint elements = p1.length;
uint inputSize = elements * 6;
uint[] memory input = new uint[](inputSize);
for (uint i = 0; i < elements; i++)
{
input[i * 6 + 0] = p1[i].X;
input[i * 6 + 1] = p1[i].Y;
input[i * 6 + 2] = p2[i].X[0];
input[i * 6 + 3] = p2[i].X[1];
input[i * 6 + 4] = p2[i].Y[0];
input[i * 6 + 5] = p2[i].Y[1];
}
uint[1] memory out;
bool success;
assembly {
success := call(sub(gas, 2000), 8, 0, add(input, 0x20), mul(inputSize, 0x20), out, 0x20)
// Use "invalid" to make gas estimation work
switch success case 0 { invalid() }
}
require(success);
return out[0] != 0;
}
/// Convenience method for a pairing check for two pairs.
function pairingProd2(G1Point memory a1, G2Point memory a2, G1Point memory b1, G2Point memory b2) internal returns (bool) {
G1Point[] memory p1 = new G1Point[](2);
G2Point[] memory p2 = new G2Point[](2);
p1[0] = a1;
p1[1] = b1;
p2[0] = a2;
p2[1] = b2;
return pairing(p1, p2);
}
/// Convenience method for a pairing check for three pairs.
function pairingProd3(
G1Point memory a1, G2Point memory a2,
G1Point memory b1, G2Point memory b2,
G1Point memory c1, G2Point memory c2
) internal returns (bool) {
G1Point[] memory p1 = new G1Point[](3);
G2Point[] memory p2 = new G2Point[](3);
p1[0] = a1;
p1[1] = b1;
p1[2] = c1;
p2[0] = a2;
p2[1] = b2;
p2[2] = c2;
return pairing(p1, p2);
}
/// Convenience method for a pairing check for four pairs.
function pairingProd4(
G1Point memory a1, G2Point memory a2,
G1Point memory b1, G2Point memory b2,
G1Point memory c1, G2Point memory c2,
G1Point memory d1, G2Point memory d2
) internal returns (bool) {
G1Point[] memory p1 = new G1Point[](4);
G2Point[] memory p2 = new G2Point[](4);
p1[0] = a1;
p1[1] = b1;
p1[2] = c1;
p1[3] = d1;
p2[0] = a2;
p2[1] = b2;
p2[2] = c2;
p2[3] = d2;
return pairing(p1, p2);
}
}
contract CVC {
using Pairing for *;
struct VerifyingKey {
Pairing.G1Point a;
Pairing.G2Point b;
Pairing.G2Point gamma;
Pairing.G2Point delta;
Pairing.G1Point[] gamma_abc;
}
struct Proof {
Pairing.G1Point a;
Pairing.G2Point b;
Pairing.G1Point c;
}
function verifyingKey() pure internal returns (VerifyingKey memory vk) {
vk.a = Pairing.G1Point(uint256(0x040c25fc4789e3be4030ec734962fa634f697d7fb40d6c8fd05a0a26b2e4bbdc), uint256(0x1952d16a501e559beb17fceafca1e1145fbfac88fe464c5a56009b6ec2cd0749));
vk.b = Pairing.G2Point([uint256(0x1128f1935e0d096177555b680ae3f88979bde4491abdeacb69959d16baae2492), uint256(0x1fff28ca31727477fa5967bc3f9a8fabc19fb66c0f73f2c1deb970fe82f7f88f)], [uint256(0x0d73c74b2a151356db394753aeee2019f1be286e6e439620e8d31609b9931670), uint256(0x1aebf0f0bea297def5b0afcd8f07b6763f4b210cb2644c61e8b0a96d8aa29f63)]);
vk.gamma = Pairing.G2Point([uint256(0x17b830425c19fcaac70e3aed973cff29a2bda118496d256f605d99128e810d6e), uint256(0x1c2874a7f2c0261295d5bc9fd185f92b09a79f55cca5fe3a18a3958b9ee923f3)], [uint256(0x127259d40080d801383da34e93ed656c4eb845cf425a57fb6a9635d962e2cc51), uint256(0x2950db7d050f3945aff9a28c13e52c8c7e46a4be24b83c45f5cedfbf416f35a2)]);
vk.delta = Pairing.G2Point([uint256(0x0453affcd9fb3bb1f799335d35595c1afc0ab9c5b7903fd8474442714f61ee60), uint256(0x2df84d766e632a2ceff923712556a5367009530bfbcccdaf4775ad0834eb85b9)], [uint256(0x20ba7d68217431dc0485c69321daca807aea2bb6ec78a13ca0377a6dbfb23f64), uint256(0x09d1e5f6e4f0bb0ab0125554eff9e4bbb81ac050b60576e98a676ef9350982ec)]);
vk.gamma_abc = new Pairing.G1Point[](6);
vk.gamma_abc[0] = Pairing.G1Point(uint256(0x1058fe94fb4b390c4ab3c2a3327c663d01911853c28e1f944d3c5292730cbd7d), uint256(0x2d4a506f931551ed5133f9b24752846cbd174231e2b998ef08208ccf13daa378));
vk.gamma_abc[1] = Pairing.G1Point(uint256(0x1c1b4912eb2bff3570787ebed6470e779cb910b5d05e43f06e2c73e80d5e4fd9), uint256(0x292dced20978d7d91a30c4f85db4c4efddc4c03c076a999bef9069e150c5ddd1));
vk.gamma_abc[2] = Pairing.G1Point(uint256(0x1604bd3d8992736c644294fa3f876924e0cf5af429d187c47be860a58185e5b7), uint256(0x04ee5178cd96f4a5e8b4b6428731e0b09a53a1e6e8d53c244532dfa3dced513c));
vk.gamma_abc[3] = Pairing.G1Point(uint256(0x1a5cb8fed48e2cc93d1da72ab20180946c9116fd35c9d605d4a56c8ea118540c), uint256(0x19e9e0fc2729ff64ff106d8282db3e78735f147bcbd9e53913e020e267abf59e));
vk.gamma_abc[4] = Pairing.G1Point(uint256(0x04b6f731e0f08c65b4e57c9548e735ba49fec7ef7802bfe1cf4f87bcca652817), uint256(0x2050c461a809549fa589f680375b6d78490962cf62d842c01bacbef4c0bf987f));
vk.gamma_abc[5] = Pairing.G1Point(uint256(0x2475a57830c18369133184c596dfeade07b2c22591fab0034a732f22f7ea80c2), uint256(0x0a252aad36a468e8e891f5e2fca952675f48e21bb572b796f4ca1b157683b94c));
}
function verify(uint[] memory input, Proof memory proof) internal returns (uint) {
uint256 snark_scalar_field = 21888242871839275222246405745257275088548364400416034343698204186575808495617;
VerifyingKey memory vk = verifyingKey();
require(input.length + 1 == vk.gamma_abc.length);
// Compute the linear combination vk_x
Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);
for (uint i = 0; i < input.length; i++) {
require(input[i] < snark_scalar_field);
vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.gamma_abc[i + 1], input[i]));
}
vk_x = Pairing.addition(vk_x, vk.gamma_abc[0]);
if(!Pairing.pairingProd4(
proof.a, proof.b,
Pairing.negate(vk_x), vk.gamma,
Pairing.negate(proof.c), vk.delta,
Pairing.negate(vk.a), vk.b)) return 1;
return 0;
}
event Verified(string s);
function claimPKVerify(
uint[2] memory a,
uint[2][2] memory b,
uint[2] memory c,
uint[5] memory input,
address sender
) public returns (bool r) {
Proof memory proof;
proof.a = Pairing.G1Point(a[0], a[1]);
proof.b = Pairing.G2Point([b[0][0], b[0][1]], [b[1][0], b[1][1]]);
proof.c = Pairing.G1Point(c[0], c[1]);
uint[] memory inputValues = new uint[](input.length + 1); // 在原有的输入数组长度上增加一个额外位置
for(uint i = 0; i < input.length; i++){
inputValues[i] = input[i];
}
inputValues[input.length] = uint(sender); // 将发送者地址转换为 uint 类型并添加到输入数组末尾
if (verify(inputValues, proof) == 0) {
emit Verified("Transaction successfully verified.");
return true;
} else {
return false;
}
}
}
contract RVC {
using Pairing for *;
struct VerifyingKey {
Pairing.G1Point a;
Pairing.G2Point b;
Pairing.G2Point gamma;
Pairing.G2Point delta;
Pairing.G1Point[] gamma_abc;
}
struct Proof {
Pairing.G1Point a;
Pairing.G2Point b;
Pairing.G1Point c;
}
function verifyingKey() pure internal returns (VerifyingKey memory vk) {
vk.a = Pairing.G1Point(uint256(0x24bcb7996d85be5d9f7d1295f9e2506d3177ffa9d7ca329aba36c0d978d8be1f), uint256(0x10d336469bcae09aeba5ef514b10e7678e429c2a6b71bc815f3e7c964411daf8));
vk.b = Pairing.G2Point([uint256(0x051df0aa2aedfc7923fe58b173378da25a790f947bf69474a112fbfe1474c2c2), uint256(0x2b8d8c7f5a09fbe30b0ebfa38d17a56081dfa0d366b166bf68b65bf962a5501f)], [uint256(0x03ae12e9974ced8eb99fa6463bb267fe0548a5910cdedbf13d9eebfa6210dd11), uint256(0x0b6e18cd7bf7612e2dfc3709ff4c84194691131f04111479e3b59ee48a41047e)]);
vk.gamma = Pairing.G2Point([uint256(0x19aaad3888d3d5924be12694b588298bb19b55e5a347e8277c50ae2dd2ec8ef2), uint256(0x0a60aee7371d4044e86d8ae29dc4312763ea0e405ff22a711260e51f5106be4a)], [uint256(0x022795508f9f366b781e6ccd81059d401970d6cd5714feb1c2e5f6cd52273330), uint256(0x28f4199934a4fcadab69f13631f6f0c739faf3e007762f62f0de81770b10fbae)]);
vk.delta = Pairing.G2Point([uint256(0x0e0ec3f6413793a9f9abfff54b59278413610082f1c764e118ce81d735a041b2), uint256(0x0fdde4afb23307b1e49845438e2c2d4b952da2aec875c83ac84bb98940df8e05)], [uint256(0x08a64b3cdc9f78a24876da0c8ceb6a7bc84b825e1c54f773be218a03713ece4c), uint256(0x1d450d86dd7ae07171403ae8e8a2d81ad88d11526fb9509d20040ef491ef5765)]);
vk.gamma_abc = new Pairing.G1Point[](8);
vk.gamma_abc[0] = Pairing.G1Point(uint256(0x30481d3e3c8fce2b4a736911fff34ceb0e9aea241dadc984eaed3e210ec60d77), uint256(0x25293a548846d71c5c7af18d56a8c79121fd9ae48ddc795f78fdc82e24b26f22));
vk.gamma_abc[1] = Pairing.G1Point(uint256(0x2ae5543b4079071b46dc1409003de64f9b21f806f6a52810ab5254d77ce872fb), uint256(0x2143f716dba471c9710eff5310698280284a47faff2df502015ec569aee33b63));
vk.gamma_abc[2] = Pairing.G1Point(uint256(0x00cfe0b05e092660e8336deaefe11ac0287caa5fe6a6247c0265d30d4bfd7bb2), uint256(0x0f4dabd5c3dac5539a0537b9d2eef9c78eb3e342e8599f18f406fa0f58f036d6));
vk.gamma_abc[3] = Pairing.G1Point(uint256(0x1c7304bf08fbf6325441dc9d84d88a3d8f787f1ac952b192afe7214d10be3b95), uint256(0x2a07571d0f18591f6212ff72bcd4e26793e8f5562150f53341fd8d9ec1686424));
vk.gamma_abc[4] = Pairing.G1Point(uint256(0x28462f408ec2303119e9762f3b8e363780a08930975e3de96c3d927d3f0b1e01), uint256(0x045cb347f1d5e752c383965971d5dce5caa0b1290b9824c3258fda13a4c6c39d));
vk.gamma_abc[5] = Pairing.G1Point(uint256(0x1f877e2b310859ccc8e5f5dcf729fd1ebcac87b9d3363e35a8ea0bfa3a5bd45a), uint256(0x0af3d6b8a7655003cb2a494930da28dc45874c20a8b998e4743cf8c5dfb10bd9));
vk.gamma_abc[6] = Pairing.G1Point(uint256(0x2250078766e26e488dbd1fc8f5e538392bd0f5dbc74080c60cb58264ffc605fa), uint256(0x2fd616bbd5cf2f65ec20deeec7e2b46368ad7b203b3fce6d1083e6b8ae65e1ba));
vk.gamma_abc[7] = Pairing.G1Point(uint256(0x0308f8c4ae08e6ac68f25c65ed7902a2383b6bcbc3e5afc6d1994b7e3b8281de), uint256(0x051190e7ef38768a3a56921ef02744fe213ae53577cc75905f781cd635bc618a));
}
function verify(uint[] memory input, Proof memory proof) internal returns (uint) {
uint256 snark_scalar_field = 21888242871839275222246405745257275088548364400416034343698204186575808495617;
VerifyingKey memory vk = verifyingKey();
require(input.length + 1 == vk.gamma_abc.length);
// Compute the linear combination vk_x
Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);
for (uint i = 0; i < input.length; i++) {
require(input[i] < snark_scalar_field);
vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.gamma_abc[i + 1], input[i]));
}
vk_x = Pairing.addition(vk_x, vk.gamma_abc[0]);
if(!Pairing.pairingProd4(
proof.a, proof.b,
Pairing.negate(vk_x), vk.gamma,
Pairing.negate(proof.c), vk.delta,
Pairing.negate(vk.a), vk.b)) return 1;
return 0;
}
event Verified(string s);
function responseSKVerify(
uint[2] memory a,
uint[2][2] memory b,
uint[2] memory c,
uint[7] memory input,
address sender // 添加地址参数
) public returns (bool r) {
Proof memory proof;
proof.a = Pairing.G1Point(a[0], a[1]);
proof.b = Pairing.G2Point([b[0][0], b[0][1]], [b[1][0], b[1][1]]);
proof.c = Pairing.G1Point(c[0], c[1]);
uint[] memory inputValues = new uint[](input.length);
for(uint i = 0; i < input.length; i++){
inputValues[i] = input[i];
}
inputValues[input.length] = uint(sender); // 将发送者地址转换为 uint 类型并添加到输入数组末尾
if (verify(inputValues, proof) == 0) {
emit Verified("Transaction successfully verified.");
return true;
} else {
return false;
}
}
}ARC.sol(1+2+3+4)
pragma solidity ^0.5.0;
contract ARC{
struct token{
bytes32 encryptedName; // Encrypted name
bytes32 encryptedValue; // Encrypted value
string name;
string value;
address creator;
bytes32 hash;
bool exisit;
bool claimed;
bytes32 creatorHash;
}
address owner;
mapping(bytes32 => token) tokens;
mapping(bytes32 => bool) public claimedTokens;
event LogTokenCreate(bytes32, string, string, address, bytes32);
event LogTokenRevocation(bytes32);
event LogTokenClaim(bytes32 tokenId, address claimer);
modifier onlyOwner() {
require(msg.sender == owner, "You are not the owner");
_;
}
constructor() public {
owner = msg.sender;
}
modifier onlyCreator(bytes32 _tokenId) {
require(msg.sender == tokens[_tokenId].creator, "You are not the creator of this token");
_; // 执行原函数
}
function encryptData(string memory data, string memory key) private pure returns (bytes32) {
// Here, you can use more advanced encryption algorithms.在这里,您可以使用更高级的加密算法。
// For simplicity, we use a basic XOR encryption as an example.为了简单起见,我们使用一个基本的XOR加密作为示例。
bytes memory dataBytes = bytes(data);
bytes memory keyBytes = bytes(key);
bytes memory encryptedData = new bytes(dataBytes.length);
for (uint256 i = 0; i < dataBytes.length; i++) {
encryptedData[i] = dataBytes[i] ^ keyBytes[i % keyBytes.length];
}
return keccak256(encryptedData);
}
function decryptData(bytes32 encryptedData, string memory key) private pure returns (string memory) {
// Here, you should implement the decryption logic that matches the encryption logic.在这里,您应该实现与加密逻辑匹配的解密逻辑。
bytes memory dataBytes = abi.encodePacked(encryptedData);
bytes memory keyBytes = bytes(key);
bytes memory decryptedData = new bytes(dataBytes.length);
for (uint256 i = 0; i < dataBytes.length; i++) {
decryptedData[i] = dataBytes[i] ^ keyBytes[i % keyBytes.length];
}
return string(decryptedData);
}
function getTokenData(bytes32 tokenId, string memory decryptionKey) public view returns (string memory, string memory, bytes32, address, bool, bool) {
require(tokens[tokenId].exisit, "Token does not exist");
string memory name = decryptData(tokens[tokenId].encryptedName, decryptionKey);
string memory value = decryptData(tokens[tokenId].encryptedValue, decryptionKey);
bytes32 creatorHash = tokens[tokenId].creatorHash;
address creator = tokens[tokenId].creator;
bool exisit = tokens[tokenId].exisit;
bool claimed = tokens[tokenId].claimed;
return (name, value, creatorHash, creator, exisit, claimed);
}
function tokenCreate(string memory _name, string memory _value, bytes32 _hash)public returns (bytes32) {
//bytes32 tokenId = sha256(abi.encodePacked(_name,_value,msg.sender,_hash,now));
bytes32 tokenId = sha256(abi.encodePacked(_name,_value,_hash,_name));
tokens[tokenId].name = _name;
tokens[tokenId].value = _value;
tokens[tokenId].creator = msg.sender;
tokens[tokenId].hash = _hash;
tokens[tokenId].exisit = true;
tokens[tokenId].claimed = false;
emit LogTokenCreate(tokenId, _name, _value, msg.sender, _hash);
return tokenId;
}
// function tokenRevocation(bytes32 _tokenId)public {
// address creator = creatorQuery(_tokenId);
// if (msg.sender == creator){
// revocation(_tokenId);
// emit LogTokenRevocation(_tokenId);
// }
// }
function tokenRevocation(bytes32 _tokenId) public onlyCreator(_tokenId) {
revocation(_tokenId);
emit LogTokenRevocation(_tokenId);
}
function changeStatus(bytes32 _tokenId)public {
tokens[_tokenId].claimed = true;
}
function revocation(bytes32 _tokenId)public {
tokens[_tokenId].exisit = false;
}
// function creatorQuery(bytes32 _tokenId)public view returns(address){
// address creator = tokens[_tokenId].creator;
// return creator;
// }
function exisitQuery(bytes32 _tokenId)public view returns(bool){
bool exisit = tokens[_tokenId].exisit;
return exisit;
}
function claimedQuery(bytes32 _tokenId)public view returns(bool){
bool claimed = tokens[_tokenId].claimed;
return claimed;
}
function tokenQuery(bytes32 _tokenId)public view returns(bytes32, string memory, string memory, bytes32, address, bool, bool){
string memory name = tokens[_tokenId].name;
string memory value = tokens[_tokenId].value;
bytes32 hash = tokens[_tokenId].hash;
address creator = tokens[_tokenId].creator;
bool exisit = tokens[_tokenId].exisit;
bool claimed = tokens[_tokenId].claimed;
return (_tokenId, name, value, hash, creator, exisit, claimed);
}
function claimToken(bytes32 tokenId, address claimer) public onlyOwner {
require(tokens[tokenId].exisit, "Token does not exist");
require(!claimedTokens[tokenId], "Token already claimed");
require(claimer == tokens[tokenId].creator, "Invalid claimer");
// Here, you can perform additional verification steps if needed, such as multi-signature verification or additional checks.
claimedTokens[tokenId] = true;
tokens[tokenId].claimed = true;
emit LogTokenClaim(tokenId, claimer);
}
function restoreToken(bytes32 _tokenId) public onlyOwner {
require(claimedTokens[_tokenId], "Token is not revoked");
tokens[_tokenId].exisit = true;
tokens[_tokenId].claimed = false;
claimedTokens[_tokenId] = false;
emit LogTokenRevocation(_tokenId);
}
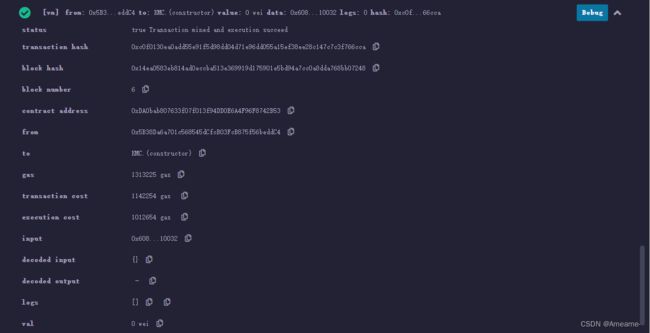
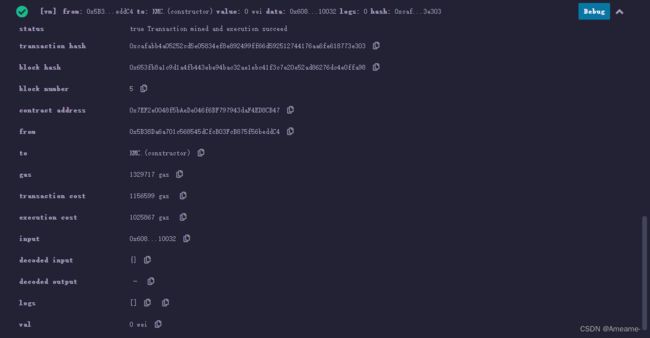
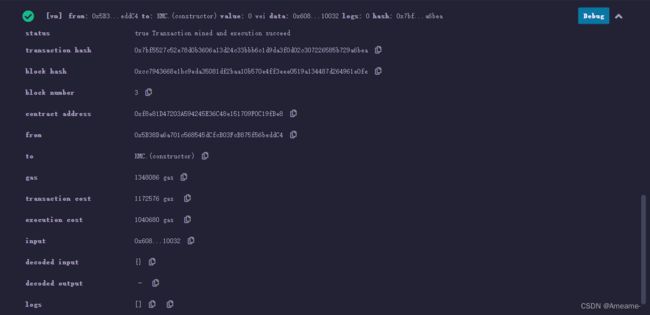
}gas比较
kmc.sol原版
kmc.sol改进(1)
kmc.sol改进(1+2)
kmc.sol改进(1+2+3)
ARC.sol改进(1)
ARC.sol改进(1+2)
ARC.sol改进(1+2+3)(大改)
ARC.sol改进(1+2+3+4)
ARC.sol改进(1+2+3+4+5)