【UnityShader入门精要学习笔记】第四章(2)点和向量
![]()
本系列为作者学习UnityShader入门精要而作的笔记,内容将包括:
- 书本中句子照抄 + 个人批注
- 项目源码
- 一堆新手会犯的错误
- 潜在的太监断更,有始无终
总之适用于同样开始学习Shader的同学们进行有取舍的参考。
文章目录
- 复习
-
- 知识点复习
-
- 左右手坐标系
- Unity中的坐标系
- 上章节练习题答案
- 点和向量
-
- 定义
- 点和向量的区别
- 去看线性代数的本质!
- 向量运算
-
- 向量加减
- 向量乘除
- 向量模长
- 归一化
- 向量的点积
- 向量叉乘
- 练习题
(该系列笔记中大多数都会复习前文的知识,特别是前文知识非常重要的时候,这是为了巩固记忆,诸位可以直接通过目录跳转)
复习
知识点复习
上节我们学习了笛卡尔坐标系(正交坐标系)。笛卡尔坐标系中包含了以下要素:
- 原点,它是整个坐标系的中心,我们以0坐标代表该点
- n维笛卡尔坐标系中的n个轴都是两两正交的,例如三维笛卡尔坐标系中xy,xz,yz都互相垂直。
我们以每条轴箭头指向的方向为正方向,反向为负方向。以正方向上的单位长度称为基向量( 或者基底 ,或者标准正交基)。
(在三维软件中,我们喜欢以红色直线代表x轴,绿色直线代表y轴,蓝色直线代表z轴)
左右手坐标系

在三维坐标系中,有两种不同的坐标系——左手坐标系和右手坐标系,判断坐标系是哪种的方法就是如上图所示,伸出左手(右手),大拇指指向x轴正方向,食指指向y轴正方向,中指指向z轴正方向,如果其中任意两轴方向对齐,而另一条轴方向相反,证明不是当前手的坐标系。
如果两个坐标系都是左手(右手)坐标系的话,那么这两个坐标系经过一系列旋转一定是可以重合的,这种性质被我们称为旋向性 。

在左手坐标系中,判断旋转正方向的方法是左手法则(右手坐标系中则是右手法则)。判断方法是,手虚握坐标轴,大拇指指向正方向,四指弯曲方向就是旋转正方向。
我们之所以要引入坐标系,其根本目的就是为了在空间中描述某个点的位置。而在Unity等等三维软件中,我们固定了一个唯一的初始坐标,才能够统一的描述这个三维软件的空间内的所有物体。
Unity中的坐标系
Unity中,对于模型空间和世界空间,Unity使用的是左手坐标系。
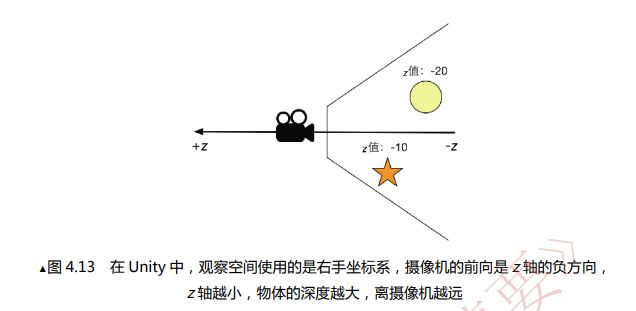
而对于观察空间来说,Unity使用的是右手坐标系。简单来说就是以摄像机为原点的坐标系,再这个坐标系中,摄像机的镜头方向是z轴的负方向(也就是z轴的正方向实际上是从屏幕指向屏幕前的你),这与模型空间和世界空间中的定义相反,z轴的减少意味着场景深度的增加。
上章节练习题答案
- 伸出左手,大拇指指向右方,食指指向前方,发现中指指向下方,和题中坐标系不重合,证明该坐标系是右手坐标系。
- 如下图所示:
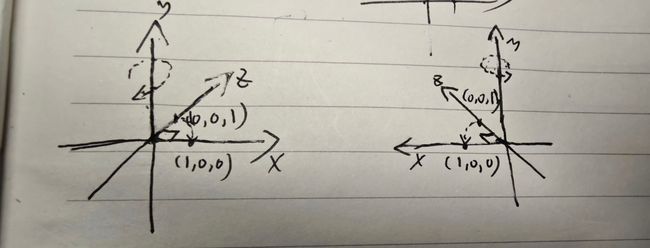
左边是一个左手坐标系,右边是一个右手坐标系,我们先找到对应的(0,0,1)点,然后按题目要求绕y轴旋转。其中左手坐标系的旋转方向用左手法则发现正方向是绕y轴顺时针,右手坐标系的旋转方向则用右手法则发现正方向是绕y轴逆时针。因此进行相应旋转,旋转90°后点落在x轴上。二者答案都为(1,0,0)。
在上图中画出的两个坐标系,虽然点的坐标是相同的,但如果将两坐标系原点重合(置于同一空间下),并用左手坐标系来统一描述两点的坐标(忽略右手坐标系的z轴)。那么点1坐标为(1,0,0),点2坐标则为(-1,0,0),如下图4.51所示:
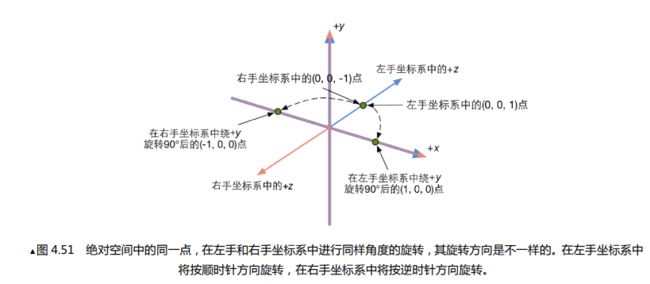

(上图4.50虽然两点重合在了同一坐标,但两个坐标系并不在同一空间,因为z轴的正方向不一致)
- 如图所示:

小球相对于摄像机的深度值为10,而根据视锥方向可知,小球目前在摄像机的镜头前向,而该方向实际上是观察空间的z轴的反方向(从屏幕到屏幕前的人的方向为正方向),因此小球在观察空间的坐标应为(0,1,-10),z值为-10。
而在以摄像机为坐标建立的模型空间下,由于模型空间是左手坐标系,因此用左手对准上图中的x,y轴,发现两个坐标系重合(当然了,因为unity中的坐标系就是左手坐标系嘛),因此确定小球在摄像机的模型空间下的坐标为(0,0,10),因此z值为10。
点和向量
定义
点(point) 是n维空间中的一个位置,它没有大小,宽度这些概念。一个空间是由无数的点构成的,我们可以用任意点的坐标描述物体在该空间中的位置。在二维,三维笛卡尔坐标系中,我们用实数来表示点的坐标,例如 P = ( P x , P y ) P=(P_x,P_y) P=(Px,Py), P = ( P x , P y , P z ) P=(P_x,P_y,P_z) P=(Px,Py,Pz)
向量(vector,或者矢量,但我建议还是叫做向量)。几何定义上讲,向量是n维空间中包含了模长(magnitude) 和方向(direction) 的有向线段 。向量与标量(scalar) 要作区分:标量只有模长,没有方向。
对于向量的表示,我们可以使用 v = ( a , b ) \bold v =(a,b) v=(a,b)来表示【实际上我更喜欢用数学的方式 v → = ( a , b ) \overrightarrow v=(a,b) v=(a,b)来表示,用箭头更能表示它是有方向的】
其中,a,b代表了其在对应的轴方向上的长度(以坐标系的基向量为单位长度)。
与书中有所不同,接下来我会用小写字母 a , b , x , y , z a,b,x,y,z a,b,x,y,z表示标量
用带箭头的字母 v → , a → , b → \overrightarrow v , \overrightarrow a, \overrightarrow b v,a,b 表示向量
用大写字母 A , B , C , D A,B,C,D A,B,C,D等表示矩阵
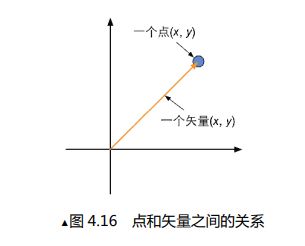
如上图所示,一个向量通常由一个箭头表示,我们以箭头方向称为向量的头,另一端称为向量的尾。在坐标系(线性代数)中,以原点为尾,指向的坐标点为头。
(注意,此处我不建议大家看书中原作者对向量的解释,原作者的解释大多是从物理角度出发,但是学习线性代数,我们需要从数学的视角,从数字上和几何上理解向量,因此我依然推荐大家去看b3b1的线性代数的本质 - 01 - 向量究竟是什么?)
原作者说向量可以表示相对于某个点的偏移,因此可以在空间中移动。但是线性代数中不要随便移动一个向量,向量一定以原点为尾,指向的坐标点为头。因为 v → = ( a , b ) \overrightarrow v=(a,b) v=(a,b)向量是以原点为起点,坐标系的基底为单位长度来描述该向量相对于原点的偏移,因此我们不能随意改变它在坐标系中的位置。
只有在进行向量计算的时候,我们才允许向量移动,将一个向量的头部或尾部对齐到其他向量的头部上。但是最终结果得到的向量,依然是原点为尾,指向的坐标点为头的向量
点和向量的区别
还是看上图,如果我们把点和向量放在同一个坐标系下,我们会发现二者虽然数学上的表示方式一样,但是在空间上,向量是从原点出发,指向目标点的。也就是说任何一个点都可以由一个向量表示。
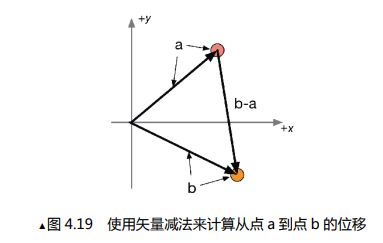
那么点和向量区别在哪呢?虽然二者都可以用(x,y)来表示,但是注意,向量之所以用这种方式来表示,是因为我们默认它的尾部为原点。实际上应该是(x-0,y-0)。向量的表示实际是两个点之间坐标的差值(顶部点减去尾部点)。
如果我们用矩阵的方式来表示向量:例如 v → = [ x y ] \overrightarrow v = \begin{bmatrix}x\\ y\end{bmatrix} v=[xy]。那么实际上表示的是 v → = [ x i ^ y j ^ ] \overrightarrow v = \begin{bmatrix}x \hat i\\ y\hat j\end{bmatrix} v=[xi^yj^]。 ( i ^ , j ^ ) (\hat i,\hat j) (i^,j^)就是当前向量的基向量,对应在这个笛卡尔坐标系下就是x正向上的单位长度,和y正向上的单位长度。
那么如果我们任意改变x和y的值?这样的话,其实意味着对基向量的任意拉伸组合,最终我们可以得到的向量将遍布整个二维空间,我们将其称为基向量所组成的张成空间(span space) 。
如果用向量来遍布整个空间,实在太过拥挤,最终我们会用向量的终点来表示这个向量,因此,向量就表示为了点。
去看线性代数的本质!
好吧,看书中的这些文字其实不如去复习一遍线性代数的本质,接下来部分参考价值不大的内容我就省略过了。
向量运算
向量加减
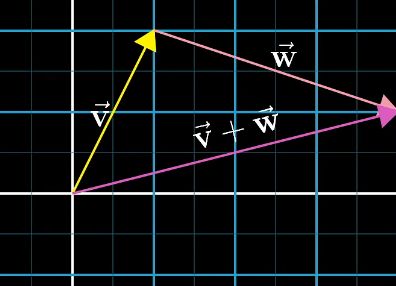
假设有向量a和向量b,则:
a → + b → = ( a x + b x , a y + b y ) a → − b → = ( a x − b x , a y − b y ) \overrightarrow a+\overrightarrow b=(a_x+b_x,a_y+b_y) \newline \overrightarrow a-\overrightarrow b = (a_x-b_x,a_y-b_y) a+b=(ax+bx,ay+by)a−b=(ax−bx,ay−by)
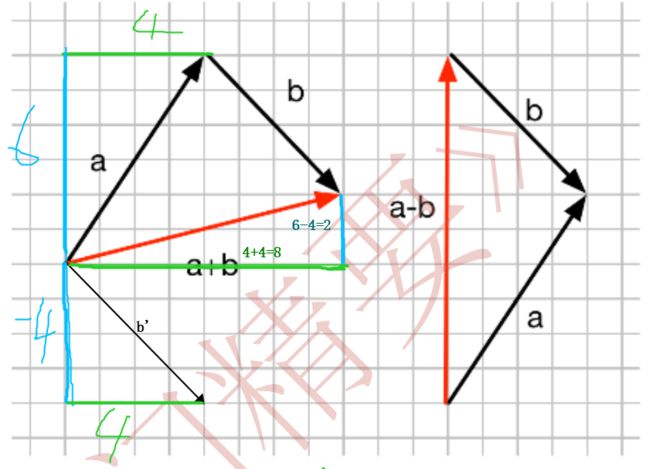
几何上看,向量相加减,则可以用向量计算的三角形法则得出结果向量。矩阵上来看,以左图向量相加为例,我们将b向量移动到对应原点位置成 b ′ b' b′。然后将 a 和 b ′ a和b' a和b′在xy轴上的分量进行相加,发现最终结果和三角形法则画出的是一模一样的。
向量乘除
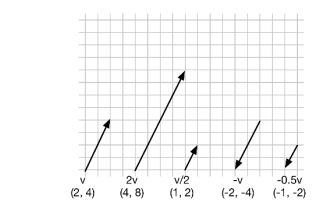
我们可以用一个标量来对向量进行乘除:
k v → = ( k x , k y , k z ) v → / k = ( x k , y k , z k ) k\overrightarrow v=(kx,ky,kz) \newline \overrightarrow v/k=(\frac{x}{k},\frac{y}{k},\frac{z}{k}) kv=(kx,ky,kz)v/k=(kx,ky,kz)
还记得标量的英文吗?Scaler ,我认为很形象,如果在几何上看,其实最终结果就是对一个向量进行缩放(拉伸),缩放的英文不就是Scale吗。(上图对于向量的拉伸不太准确,应当保持起点不变,终点拉伸到对应坐标)
向量模长
模长公式:
∣ v → ∣ = x 2 + y 2 + z 2 |\overrightarrow v| = \sqrt{x^2+y^2+z^2} ∣v∣=x2+y2+z2
简单的计算,因为几何上直观来看就是运用了勾股定理。
归一化
想起学习线代时的痛点之一施密特正交化,根据线性无关的向量组构造一个标准正交化向量组。反正怎么正交化已经忘了,但是如何归一化还是记得的。
给定任意非零向量 v → \overrightarrow v v,将其归一化为模长为1的单位向量,归一化公式为:
v ^ = v → ∣ v → ∣ \hat v = \frac{\overrightarrow v}{|\overrightarrow v|} v^=∣v∣v ,即该向量除以其模长
![]()
归一化的单位向量模长为1,因此所有归一化向量可以构成一个单位圆。其落点都在单位圆的圆周上。
在后文章节中,我们将会不断遇到法线方向,光源方向这些概念。由于我们的计算要求往往需要对应的向量是单位向量,因此使用前应当将向量先归一化。
向量的点积
向量的点积公式如下:
a → ⋅ b → = ( a x , a y , a z ) ⋅ ( b x , b y , b z ) = a x b x + a y b y + a z b z \overrightarrow a \cdot \overrightarrow b =(a_x,a_y,a_z)\cdot(b_x,b_y,b_z)=a_xb_x+a_yb_y+a_zb_z a⋅b=(ax,ay,az)⋅(bx,by,bz)=axbx+ayby+azbz
点积满足交换律,即:
a → ⋅ b → = b → ⋅ a → \overrightarrow a \cdot \overrightarrow b = \overrightarrow b \cdot \overrightarrow a a⋅b=b⋅a
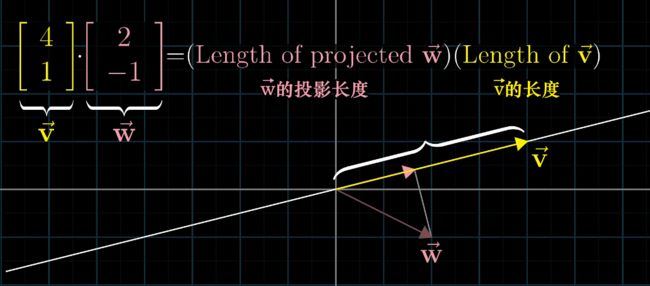
点积其实本质上计算的是投影与向量的乘积。对于 v → ⋅ w → \overrightarrow v \cdot \overrightarrow w v⋅w而言,其计算结果实质上是 w → \overrightarrow w w的投影长度 乘以 ∣ v → ∣ |\overrightarrow v| ∣v∣
什么是投影?假设有一道光源垂直于向量a所在的直线,那么b在a方向上的影子,就是b向量首尾两点作垂直,最后在a方向直线上的连线,这个线段被我们称之为投影。
![]()
根据两个向量之间的夹角,点积的符号也不同,若夹角小于90°则结果>0,若等于90°则=0,若大于90°则<0
(推荐视频:07点积与对偶性,解释了为什么点积的公式在几何上的表现是这样的。简单来说, [ v x v y ] ⋅ [ w x w y ] \begin{bmatrix}v_x\\ v_y\end{bmatrix} \cdot \begin{bmatrix}w_x\\ w_y\end{bmatrix} [vxvy]⋅[wxwy]实质上与矩阵乘法 [ v x v y ] [ w x w y ] \begin{bmatrix}v_x v_y\end{bmatrix} \begin{bmatrix}w_x\\ w_y\end{bmatrix} [vxvy][wxwy]相等,而后者计算结果实际上是将二维矩阵w应用线性变换v使其降维到了一维空间,这个一维空间就是我们用于投影的数轴,降维后的结果就是投影,所以向量点积本质上就是一个将矩阵从二维变换到一维的线性变换。)
![]()
从三角函数上看,点积公式还可以表示为下列形式:
a ⋅ b = ∣ a ∣ ∣ b ∣ c o s θ a \cdot b = |a||b|cos\theta a⋅b=∣a∣∣b∣cosθ
(其实还是投影乘以模长,投影是 ∣ b ∣ c o s θ |b|cos\theta ∣b∣cosθ,模长是 ∣ a ∣ |a| ∣a∣)
投影还有一些其他的性质:
( k a ) ⋅ b = a ⋅ ( k b ) = k ( a ⋅ b ) ——结合律 (ka) \cdot b = a \cdot(kb) = k(a \cdot b) ——结合律 (ka)⋅b=a⋅(kb)=k(a⋅b)——结合律
a ⋅ ( b + c ) = a ⋅ b + a ⋅ c ——分配律 a \cdot (b+c) = a \cdot b + a \cdot c ——分配律 a⋅(b+c)=a⋅b+a⋅c——分配律
v ⋅ v = v x 2 + v y 2 + v z 2 = ∣ v ∣ 2 v \cdot v = v_x^2 + v_y^2 +v_z^ 2 = |v|^2 v⋅v=vx2+vy2+vz2=∣v∣2
向量叉乘
另一个重要的运算是向量的叉乘(cross product) ,也称为外积(outer product) 。
叉乘的公式是:
a × b = ( a x , a y , a z ) × ( b x , b y , b z ) = ( a y b z − a z b y , a z b x − a x b z , a x b y − a y b x ) a × b =(a_x,a_y,a_z) ×(b_x,b_y,b_z) = (a_yb_z - a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x) a×b=(ax,ay,az)×(bx,by,bz)=(aybz−azby,azbx−axbz,axby−aybx)
看起来好复杂好难记,为什么是这样的?
如果用线性代数来表示的话就清晰了:

纠正一下上式子,虽然结果正确,但是没写对 τ \tau τ的计算。记该矩阵为X
d e t ( X ) = a 1 , 1 A 1 , 1 + a 1 , 2 A 1 , 2 + a 1 , 3 A 1 , 3 = i ^ ∗ ( − 1 ) 1 + 1 ( v 2 w 3 − v 3 w 2 ) + j ^ ∗ ( − 1 ) 1 + 2 ( v 1 w 3 − v 3 w 1 ) + k ^ ∗ ( − 1 ) 1 + 3 ( v 1 w 2 − v 2 w 1 ) det(X) =a_{1,1}A_{1,1}+a_{1,2}A_{1,2}+a_{1,3}A_{1,3}=\hat i *(-1)^{1+1}(v_2w_3-v_3w_2)+\hat j*(-1)^{1+2}(v_1w_3-v_3w_1)+\hat k * (-1)^{1+3}(v_1w_2-v_2w_1) det(X)=a1,1A1,1+a1,2A1,2+a1,3A1,3=i^∗(−1)1+1(v2w3−v3w2)+j^∗(−1)1+2(v1w3−v3w1)+k^∗(−1)1+3(v1w2−v2w1)
实际上叉乘就是加上一列基向量构成一个新矩阵,并计算该矩阵的行列式。
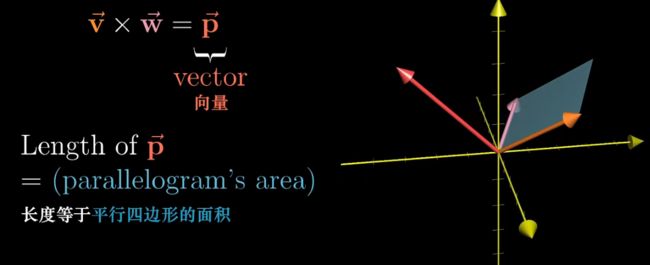
记住一个简单的结论就是,两个向量叉乘,最终会得到一个新向量,这个新向量的长度是 v , w v,w v,w向量构成的平行四边形的面积,而新向量的方向,由原坐标系指定,且垂直于这个平行四边形。如果你使用右手坐标系,就举起右手,反之使用左手,使得任意两根手指与 v , w v,w v,w对齐,剩下那根的方向就是新向量的方向。
![]()
这个叉乘出来的向量的模长由于和平行四边形面积一致,所以我们也可以得到叉乘向量的模长公式:
∣ a × b ∣ = ∣ a ∣ ∣ b ∣ s i n θ |a × b| = |a||b|sin\theta ∣a×b∣=∣a∣∣b∣sinθ (平行四边形面积=底 * 高)
叉乘是无法交换的, a × b = − ( b × a ) a × b = -(b×a) a×b=−(b×a)。
从几何意义上去理解点乘和叉乘,就会发现其中奥妙所在,为什么点乘可以交换,而叉乘无法交换:
因为点乘实质上是二维降维成一维,无论二维一维,它们都满足我们之前说的旋向性(handedness),因此可以交换。
而叉乘的三个向量建立了一个非正交的左右手三维坐标系(由原坐标系为左手还是右手指定),如果交换叉乘顺序,则产生的新向量的方向是相反的,就变成了另一只手对应的坐标系,所以结果需要加个负号。
叉乘也不满足结合律: ( a × b ) × c ≠ a × ( b × c ) (a × b) × c \ne a × (b × c) (a×b)×c=a×(b×c)
叉乘最常见的应用就是计算垂直于一个平面、三角形的向量,还可以用于判断三角面片的朝向。
练习题
- 判断题
(1)一个向量的大小不重要,只需要在正确的位置把它画出来即可
(2)点可以被认为是位置向量,这是通过把向量的尾部固定在原点得到的
(3)选择左手坐标系还是右手坐标系很重要,这会影响到叉乘的计算
2.计算题:
(1) ∣ ( 2 , 7 , 3 ) ∣ |(2,7,3)| ∣(2,7,3)∣
(2) 2.5 ( 5 , 4 , 10 ) 2.5(5,4,10) 2.5(5,4,10)
(3) ( 3 , 4 ) 2 \frac{(3,4)}{2} 2(3,4)
(4) 对 ( 5 , 12 ) 进行归一化 对(5,12)进行归一化 对(5,12)进行归一化
(5) 对 ( 1 , 1 , 1 ) 进行归一化 对(1,1,1)进行归一化 对(1,1,1)进行归一化
(6) ( 7 , 4 ) + ( 3 , 5 ) (7,4)+(3,5) (7,4)+(3,5)
(7) ( 9 , 4 , 13 ) − ( 15 , 3 , 11 ) (9,4,13)-(15,3,11) (9,4,13)−(15,3,11)
3.假设场景中有一光源位于 ( 10 , 13 , 11 ) (10,13,11) (10,13,11)处,还有一个点位于 ( 2 , 1 , 1 ) (2,1,1) (2,1,1),请问光源到点的距离是?
4.计算下列运算:
(1) ( 4 , 7 ) ⋅ ( 3 , 9 ) (4,7)\cdot (3,9) (4,7)⋅(3,9)
(2) ( 2 , 5 , 6 ) ⋅ ( 3 , 1 , 2 ) − 10 (2,5,6)\cdot (3,1,2) -10 (2,5,6)⋅(3,1,2)−10
(3) 0.5 ( − 3 , 4 ) ⋅ ( − 2 , 5 ) 0.5(-3,4)\cdot(-2,5) 0.5(−3,4)⋅(−2,5)
(4) ( 3 , − 1 , 2 ) × ( − 5 , 4 , 1 ) (3,-1,2)×(-5,4,1) (3,−1,2)×(−5,4,1)
(5) ( − 5 , 4 , 1 ) × ( 3 , − 1 , 2 ) (-5,4,1)×(3,-1,2) (−5,4,1)×(3,−1,2)
5.已知向量a和向量b,a的模长为4,b的模长为6,它们间的夹角为60°,求计算:
( s i n 60 ° = 3 2 ≈ 0.866 , c o s 60 ° = 1 2 = 0.5 ) sin60° = \frac{\sqrt{3}}{2}\approx0.866,cos60° = \frac{1}{2} = 0.5) sin60°=23≈0.866,cos60°=21=0.5)
(1) a ⋅ b a \cdot b a⋅b
(2) ∣ a × b ∣ |a×b| ∣a×b∣
6.假设,场景中有一个NPC,它位于点 p p p处,它的前方用向量 v v v表示。
(1)假设现在玩家移动到了点 x x x处,那么如何判断玩家在NPC的前方还是后方?使用上述学习的知识来描述。
(2)使用(1)中的描述方法,代入点 p = ( 4 , 2 ) , v = ( − 3 , 4 ) , x = ( 10 , 6 ) p=(4,2),v=(-3,4),x=(10,6) p=(4,2),v=(−3,4),x=(10,6)来验证答案
(3)现在,NPC只能观察到有限的视角范围,其视角角度为 ϕ \phi ϕ,也就是视野在前方左侧 ϕ 2 \frac{\phi}{2} 2ϕ到前方右侧 ϕ 2 \frac{\phi}{2} 2ϕ。那么我们如何通过点积来判断NPC是否可以看到点 x x x?
(4)在(3)的基础上,我们又要求NPC只能看见固定距离内的对象,如何判断?
7.在渲染中我们时常会需要判断一个三角面片是正面还是背面,这可以通过判断三角形的3个顶点在当前空间中是顺时针还是逆时针排序来得到。给定三角形的三个顶点 p 1 p_1 p1、 p 2 p_2 p2、 p 3 p_3 p3,假设我们使用的是左手坐标系,且 p 1 p_1 p1、 p 2 p_2 p2、 p 3 p_3 p3都位于xy平面上(即它们的z分量都为0),且人眼位于z轴的负方向上,向z轴正方形观察,如图所示:
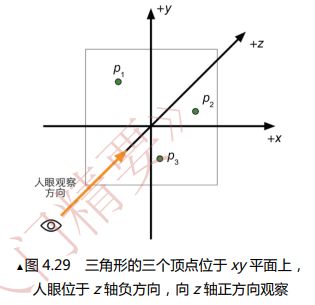
请问如何判断这三个顶点的顺序是顺时针还是逆时针?