C语言递归+DFS（深度优先搜索算法）详解 图文并茂，手把手教你画树状图

目录

一.标准定义

二.跳台阶（典型递归题目）

三.递归实现指数型枚举

四.递归实现排列型枚举

五.递归实现组合型枚举

六.DFS算法模板

---

 

一.标准定义

深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。

 

说人话，其实就是沿着一条路一直搜索，知道条件不符合，就回头走到分岔口，选择另一条路继续搜索，俗称：”不撞南墙不回头“搜索。

这种一直进行下去又返回的操作是不是很像递归，dfs名字听起来高大上，其实本质就是递归。那我们就先从一道典型的递归题开始说起吧。

二.跳台阶（典型递归题目）

上楼梯的同学，每次可以⾛⼀个台阶，也可以⾛两个台阶，现在有N个台阶，请问有多少种不同的方法？（先爬1阶再爬2阶和先爬2阶再爬1阶是不同的方法）

我们可以自己在草稿纸上算算，看看有什么规律。

N=1，1种；

N=2，1+1/2   2种

N=3 1+1+1/1+2/2+1   3种

N=4 1+1+1+1/2+2/1+2+1/2+1+1/1+1+2   5种

...... 

很显然，其实你会发现答案成斐波那契数列（当然，本题答案是从斐波拉契数列第二项开始的)。这就把题目转换成我们熟悉的问题了。

对于斐波那契数列，我们可以引用一种”递归搜索树“的方法，来让整个过程更加直观。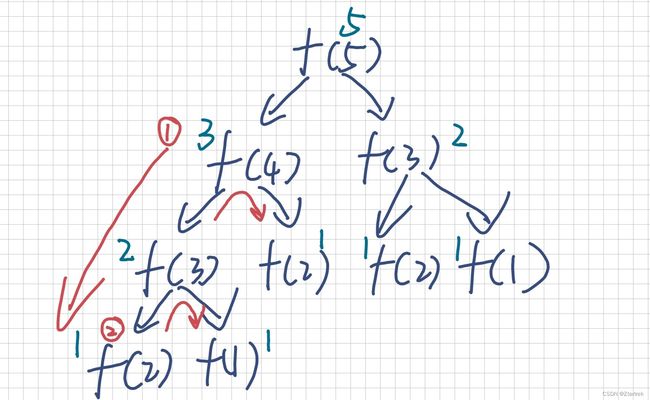 

我们先沿着左边①这条路一直往下算，直到遇到了f(2)（因为我们知道f(1),f(2)的值)，然后撞到了”南墙“，我们就开始回溯，算f(1)，两者累加算出f(3)的值，接着回溯算f(2)的值...... 

这个过程其实就体现了什么加”深度搜索“，什么叫”回溯“。

我们简单看一下这道题的代码。

#include
int fun1(int n)
{
	if (n == 1)
		return 1;
	else if (n == 2)
		return 2;
	else
		return fun1(n - 1) + fun1(n - 2);
}

什么？觉得简单？我们开始上强度了。 

三.递归实现指数型枚举

我们先看看这道题。可以尝试运用树形图的方法找找思路。

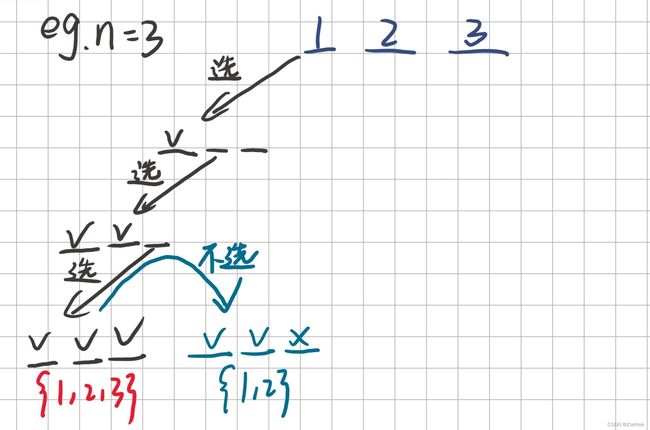
通过判断一个数选不选的思路，我们可以画出树状图。这是我没画完的树状图，你看，这样就能找到2个答案了。 

我们把图补全，8个答案就已经全部找到了。 

 接着，我们进行代码实现，注意看我的注释>

创建数组st来存放每个数的状态，它到底选没选

#include 
int n;
int st[20] = { 0 };//记录每个数的状态，0代表还没考虑，1代表选了，2代表没选
void dfs(int x)//x表示当前枚举到了哪个位置
{
	//判断是不是撞了"南墙"了
	if (x > n)
	{
		for (int i = 1; i <= n; i++)
		{
			if (st[i] == 1)
			{
				printf("%d ", i);
			}
		}
		printf("\n");
		return;
	}

	//选
	st[x] = 1;
	dfs(x + 1);
	st[x] = 0;//恢复现场（下面有解释）

	//回溯以后，就该不选了
	st[x] = 2;
	dfs(x + 1);
	st[x] = 0;
}

int main()
{
	scanf("%d", &n);
	dfs(1);//把位置1传过去
	return 0;
}

代码配合树状图更好理解，一定要切记，当一条路走不通的时候才会发生回溯！！！

为什么要恢复现场？其实就是为了恢复到上一个分岔口的状态，把数字标记为还没有考虑。这个操作可以让回溯的过程更加清晰。

看到这里，不知道你的精神状态是怎样的？如果你感到->

不要慌张，熟能生巧~

四.递归实现排列型枚举

同样的，上例题

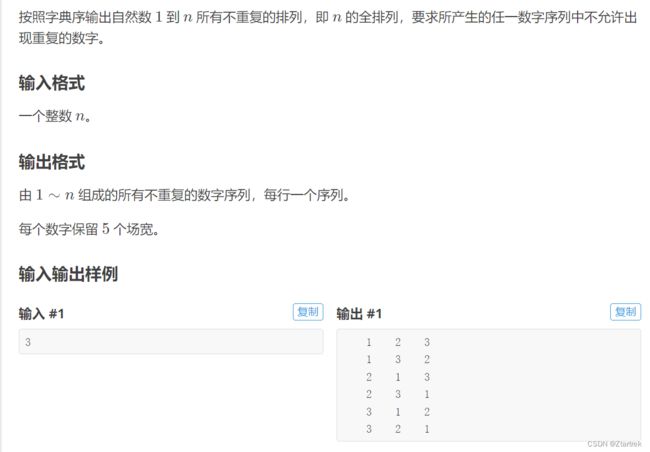
当n=3时，由高中学的排列组合知识，那么就有A3 3=3*2*1=6种排列方式，符合输出结果。

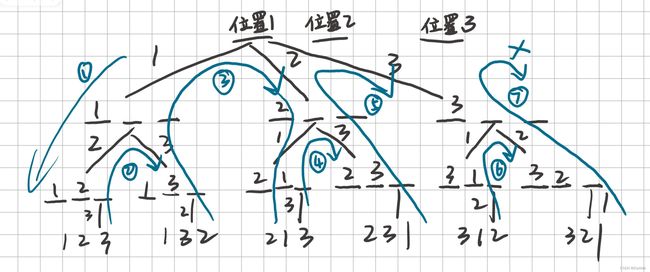
我们可以根据依次枚举一个位置上选哪个数的思路，来画个树状图，试试呢？

我们一起来看看代码如何实现的

#include 
#include 

int n = 0;
bool st[10];//因为一个数只能出现一次，所以用一个状态数组存一下一个数是否已经被选。
//true表示选过，false表示未被选。
int arr[10] = { 0 };//存的是答案，例如123/321/312

//x表示枚举到的位置
void dfs(int x)
{
	if (x>n)
	{
		for (int i = 1; i <= n; i++)
		{
			printf("%d", arr[i]);
		}
		printf("\n");
		return;
	}
	
	for (int i = 1; i <= n; i++)
	{
		if (!st[i])//如果st[i]是false
		{
			st[i] = true;
			arr[x] = i;
			dfs(x + 1);
			//恢复现场
			st[i] = false;
			arr[x] = 0;
		}
	}
}
int main()
{
	scanf("%d", &n);
	dfs(1);
	return 0;
}

大家可以运用编译器的调试功能，一步步看怎么运行的。或者自己口述整个过程的逻辑，来加深自己的理解。 

（对了，如果题目要ac的话，注意在输出的时候使用%5d就能保留5个场宽啦~）

五.递归实现组合型枚举

加油，最后一个类型了！

                                                    

我们来看题。

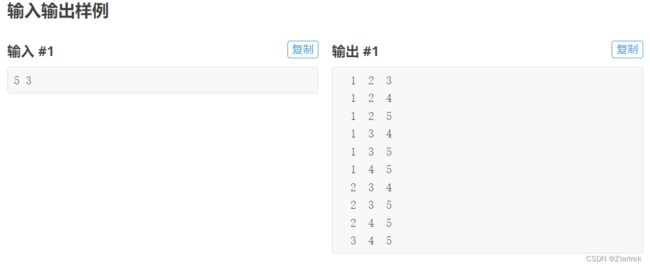
 当n=5，r=3时，由高中学的排列组合知识，不考虑顺序，那么就有C5 3=C5 2=10种排列方式，符合输出结果。

我们可以发现，每一行的数是递增的，我们也可以通过枚举一个位置上选什么数的思路来画出树状图，自己试试吧！

当一条路没有结果的时候，我们把这种舍弃它的行为称作”剪枝“。

对于代码的实现，我们运用：

int x;记录当前枚举到了哪个位置

int arr[x];记录都选了哪些数（记答案）

int start;（记录下个位置从几开始枚举）

#include 
int n, r;
int arr[21];

void dfs(int x,int start)
{
	if (x > r)
	{
		for (int i = 1; i <= r; i++)
		{
			printf("%3d", arr[i]);
		}
		printf("\n");
		return;
	}

	for (int i = start; i <= n; i++)
	{
		arr[x] = i;
		dfs(x + 1, i + 1);
		arr[x] = 0;//恢复
	}
}

int main()
{
	scanf("%d %d", &n, &r);
	dfs(1,1);
	return 0;
}

六.DFS算法模板

做了以上的题，我们可以总结出dfs算法的一个模板。

1.创建一个数组，存储状态和结果。

2.函数内部

①判断是否撞了南墙

②执行赋值，改状态的操作

③再次调用函数

④恢复现场

 恭喜，你完成了DFS算法的学习！

接下来就是刷题啦，在我的下一篇文章里，我们一起来刷题~