基于蒙特卡洛和拉丁超立方的大规模电动车充电模型(MATLAB-附案例代码)
目录
1. 摘要
2. 基本原理
2.1 蒙特卡罗抽样(Monte Carlo)
2.2.1 主要原理
2.1.2 MC优缺点
2.2 拉丁超立方体抽样(Latin hypercube sampling)
2.2.1 主要原理
3. 大规模电动车充电模型案例分析
3.1 模型构建
3.1.1 电动车日行驶里程概率分布
3.1.2 电动车充电起始时间概率分布
3.2 结果分析
3.2.1 行驶里程采样结果
3.2.2 起始充电时间采样结果
3.2.3 电动车耗电量和充电时间
3.2.4 总充电曲线对比
参考文献
附录
主程序
函数Charge_total
函数Day_Km
函数Time_In
1. 摘要
电动汽车大规模入网充电时会导致系统内负载峰值拔高的问题,和分布式电源一样,都会对电网的安全稳定运行造成冲击,需要在满足系统运行经济效益最优的同时,尽量降低大量电动汽车入网无序充电对系统造成的不良影响。本文通过蒙特卡洛(Monte Carlo,MC)和拉丁超立方(Latin hypercube sampling,LHS)仿真技术,生成大规模电动车无序充电功率曲线,分析大规模电动车接入对电网造成的影响,并对比分析了MC和LHS的模拟结果,分析了二者的区别。
2. 基本原理
2.1 蒙特卡罗抽样(Monte Carlo)
2.2.1 主要原理
蒙特卡罗抽样(MC)指使用随机数或伪随机数从概率分布中抽样的传统技术。MC主要应用于一系列包含随机行为的复杂问题,并由此衍生出一系列的算法,不同类型的概率分布中生成随机样本。
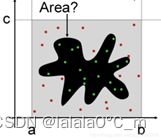
MC抽样完全是随机的——即在输入分布的范围内,样本可以落在任何位置,最经典的应用就是求解不规则图形的面积。在足够的迭代之后,蒙特卡罗抽样通过抽样“重建”输入分布。然而,MC法更有可能从高发生概率的分布区域中抽取样本,所以,当执行的迭代次数少的时候,会产生聚集的问题。
图 2.1 MC法求不规则图形面积
2.1.2 MC优缺点
(1) 优点
- 方法的误差与问题的维数无关。
- 对于具有统计性质问题可以直接进行解决。
- 对于连续性的问题不必进行离散化处理
(2)缺点
- 对于确定性问题需要转化成随机性问题。
- 误差是概率误差。
- 通常需要较多的计算步数N
当分布中包含低概率结果的时候,聚集会变得特别明显,可能会对结果产生大的影响。当这些低概率结果会对研究对象产生重要影响时,必须对这些结果进行抽样,但是如果概率非常低,少量的蒙特卡罗迭代抽样得到的结果,并不能准确代表其概率。
因此,在MC基础上衍生了分层抽样技术,如拉丁超立方体抽样。
2.2 拉丁超立方体抽样(Latin hypercube sampling)
2.2.1 主要原理
LHS抽样是抽样技术的最新进展,和MC相比,它被设计成通过较少迭代次数的抽样,准确地重建输入分布。LHS抽样的关键是对输入概率分布进行分层。分层在累积概率尺度(0 到 1)上把累积曲线分成相等的区间。然后,从输入分布的每个区间或“分层”中随机抽取样本。抽样被强制代表每个区间的值,于是,被强制重建输入概率分布。
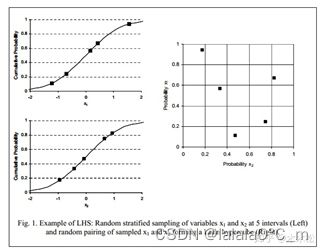
假设我们要在n维向量空间里抽取m个样本,LHS抽样的步骤是:
(1) 将每一维分成互不重迭的m个区间,使得每个区间有相同的概率 (通常考虑一个均匀分布,这样区间的长度相同)。
(2) 在每一维里的每一个区间中随机的抽取一个点;
(3) 再从每一维里随机抽出(2)中选取的点,将它们组成向量。
图 2.2 LHS原理图
作为更加高效的抽样方法,LHS在抽样效率和运行时间(由于少的迭代次数)方面带来巨大的好处。此外,如前所述,LHS对于输入概率分布中包含低概率结果情况的分析也有帮助。通过强制模拟中的抽样包含偏远事件,LHS抽样确保偏远事件在模拟的输出中被准确地代表。
3. 大规模电动车充电模型案例分析
研究使用MATLAB语言编写程序代码,并进行求解。
3.1 模型构建
3.1.1 电动车日行驶里程概率分布
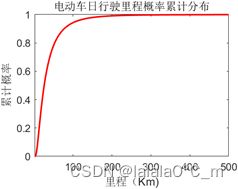
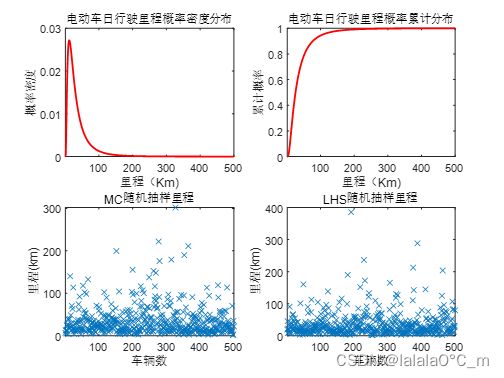
本文假设电动汽车用户日行驶里程服从对数正态分布,取均值为3.2,方差为0.88,对电动车的日行是里程进行概率描述。
其概率密度分布图和累计概率分布图如下:
 |
3.1.2 电动车充电起始时间概率分布
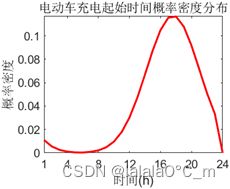
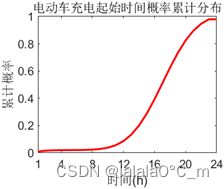
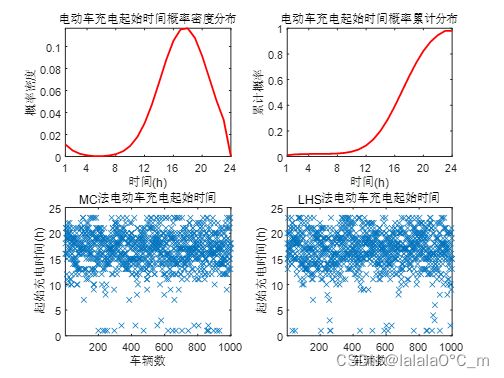
电动汽车返回时刻t服从正态分布,取均值为17.6,方差为3.4。具体概率分布表达式如下:
其概率密度分布图和累计概率分布图如下:
3.2 结果分析
研究过程中假设电动汽车各自的充电行为具有独立性的特征,每台电动汽车的电池容量、日行驶里程、起始充电时刻等都独立,表现为在己知概率分布图中随机分布的形式,因此,可以进行MC和LHS随机抽样来抽取每个步骤中的随机数,从而求取单台电动汽车的充电负荷特征,累加得出大规模电动汽车入网充电时的进行无序充电时的总充电负荷曲线。
分别设置200,500,1000辆车,抽样各场景下的行驶里程和起始充电时间,并计算电动车耗电量和充电时长,得到总负荷充电曲线。
3.2.1 行驶里程采样结果
200辆车
500辆车
1000辆车
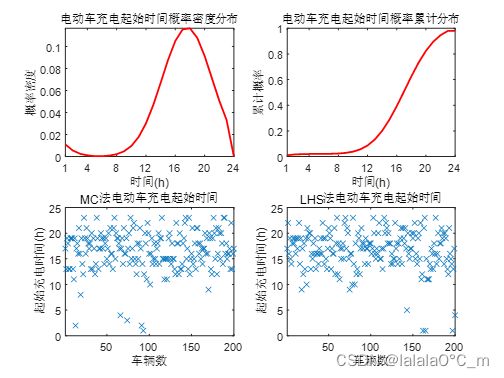
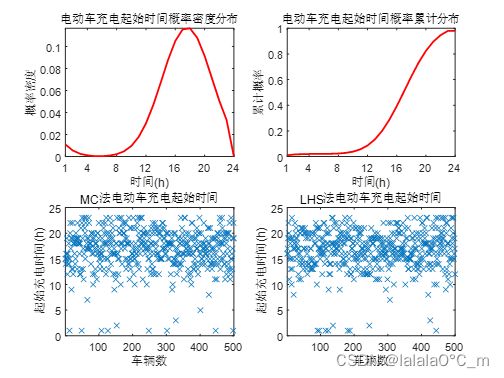
3.2.2 起始充电时间采样结果
200辆车
500辆车
1000辆车
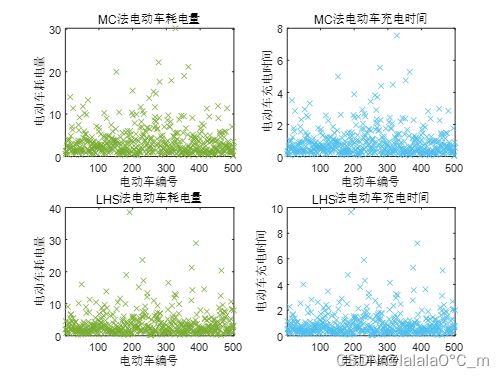
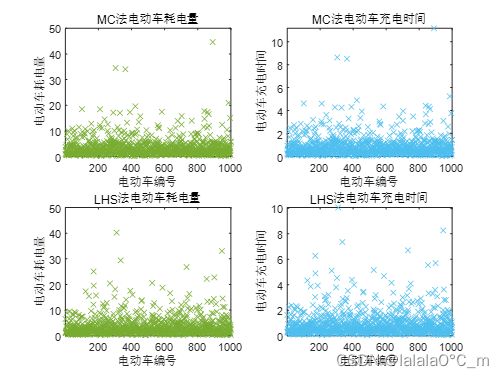
3.2.3 电动车耗电量和充电时间
200辆车
500辆车
1000辆车
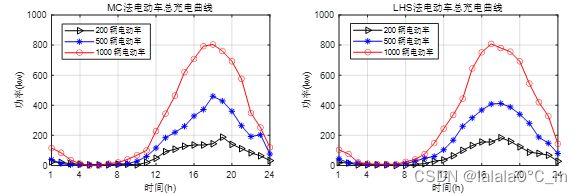
3.2.4 总充电曲线对比
不同数量的电动车的充电负荷曲线的大致走向都相同,且电动汽车充电需求集中在在16点~20点,城市管理者应该注意这段时间的电量管理。
参考文献
[1] 蒙特卡洛(Monte Carlo)方法的介绍和应用_蒙特卡洛累积图的作用_0小龙虾0的博客-CSDN博客. Blog. 蒙特卡洛(Monte Carlo)方法的介绍和应用_monte carlo中nominal值是什么意思-CSDN博客.
[2] 拉丁超立方抽样概述 - 知乎. Zhuanlan. 拉丁超立方抽样概述 - 知乎.
[3] 基于蒙特卡洛模拟的大规模电动车充电模型构建——附代码_神经网络与数学建模的博客-CSDN博客. Blog. 基于蒙特卡洛模拟的大规模电动车充电模型构建——附代码_神经网络与数学建模的博客-CSDN博客.
[4] 拉丁超立方采样(Latin hypercube sampling, LHS)及蒙特卡洛模拟简介 - 知乎. Zhuanlan. 拉丁超立方采样(Latin hypercube sampling, LHS)及蒙特卡洛模拟简介 - 知乎.
附录
本研究的代码如下,包含一个主程序 和三个函数
主程序
clc;
clear;
close all
%% 不同数量的电动车充电曲线对比
% 设置电车数量参数
N=[200 500 1000];
[PPP_MC(1,:),PPP_LHS(1,:)]=Charge_total(N(1));
[PPP_MC(2,:),PPP_LHS(2,:)]=Charge_total(N(2));
[PPP_MC(3,:),PPP_LHS(3,:)]=Charge_total(N(3));
figure('name','不同数量电动车总充电曲线对比')
subplot(1,2,1);
plot(PPP_MC(1,:),'k->');
hold on
plot(PPP_MC(2,:),'b-*');
hold on
plot(PPP_MC(3,:),'r-o');
hold off
grid on
legend('200辆电动车','500辆电动车','1000辆电动车');
title('MC法电动车总充电曲线');
xlim([1,24]);
xticks([1,4,8,12,16,20,24]);
xlabel('时间(h)');
ylabel('功率(kw)');
subplot(1,2,2);
plot(PPP_LHS(1,:),'k->');
hold on
plot(PPP_LHS(2,:),'b-*');
hold on
plot(PPP_LHS(3,:),'r-o');
hold off
grid on
legend('200辆电动车','500辆电动车','1000辆电动车');
title('LHS法电动车总充电曲线');
xlim([1,24]);
xticks([1,4,8,12,16,20,24]);
xlabel('时间(h)');
ylabel('功率(kw)');
函数Charge_total
function [P_charge_total_MC,P_charge_total_LHS]=Charge_total(N)
%% 定义电动车参数
Car.Capcity = 35; % 电动车电池容量
Car.P = 0.1; % 每公里耗电量
Car.char = 4; % 充电功率/h
%% MC+LHS抽样
% 电动车日行驶里程
[Car_km_MC,Car_km_LHS] = Day_Km(N,Car);
% 起始充电时间
[Car_in_MC,Car_in_LHS] = Time_In(N);
%% MC
W_MC = Car_km_MC*Car.P;
T_char_MC = W_MC/Car.char;
P_charge_total_MC = zeros(1,96);
P_MC = zeros(1,96);
for n = 1:N
start = Car_in_MC(n);
t = round(T_char_MC(n));
P_MC(start:start+t) = Car.char;
P_charge_total_MC = P_charge_total_MC+P_MC;
P_MC = zeros(1,96);
end
P_charge_total_MC = P_charge_total_MC(1:24)+P_charge_total_MC(25:48)…
+P_charge_total_MC(49:72)+P_charge_total_MC(73:96);
%% LHS结果
W_LHS = Car_km_LHS*Car.P;
T_char_LHS = W_LHS/Car.char;
P_charge_total_LHS = zeros(1,96);
P_LHS = zeros(1,96);
for n = 1:N
start = Car_in_LHS(n);
t = round(T_char_LHS(n));
P_LHS(start:start+t) = Car.char;
P_charge_total_LHS = P_charge_total_LHS+P_LHS;
P_LHS = zeros(1,96);
end
P_charge_total_LHS = P_charge_total_LHS(1:24)+P_charge_total_LHS(25:48)…
+P_charge_total_LHS(49:72)+P_charge_total_LHS(73:96);
%% 绘图
figure('name','电动车耗电量和充电时间')
subplot(2,2,1);
plot(W_MC,'x','Color','#77AC30');
title('MC法电动车耗电量');
xlim([1,N]);
xlabel('电动车编号');
ylabel('电动车耗电量');
subplot(2,2,2);
plot(T_char_MC,'x','Color','#4DBEEE');
title('MC法电动车充电时间');
xlim([1,N]);
xlabel('电动车编号');
ylabel('电动车充电时间');
subplot(2,2,3);
plot(W_LHS,'x','Color','#77AC30');
title('LHS法电动车耗电量');
xlim([1,N]);
xlabel('电动车编号');
ylabel('电动车耗电量');
subplot(2,2,4);
plot(T_char_LHS,'x','Color','#4DBEEE');
title('LHS法电动车充电时间');
xlim([1,N]);
xlabel('电动车编号');
ylabel('电动车充电时间');
end函数Day_Km
%% 电动车日行驶里程抽样函数
function [y3_MC,y3_LHS]=Day_Km(N,Car)
% 电动车日行驶里程概率分布(服从对数正态分布)
mu=3.2; % 均值
sigma=0.88; % 方差
y1=lognpdf(0:500,mu,sigma); % 对数正态分布密度函数
y2=logncdf(0:500,mu,sigma); % 对数正态累积分布函数
%% MC抽样
p_MC=rand(N,1);
y3_MC=logninv(p_MC,mu,sigma);
%% LHS抽样
for i=1:N
node_max(i)=i/N;
node_min(i)=(i-1)/N;
end
p_LHS=(node_max'-node_min').*rand(N,1)+node_min'; % 变换
p_LHS=p_LHS(randperm(N));
y3_LHS=logninv(p_LHS,mu,sigma); % 对数正态累积分布逆函数
%% 绘图
figure('name','电动车日行驶里程');
subplot(2,2,1)
plot(1:500,y1(1:500),'r-','Linewidth',1.5);
title('电动车日行驶里程概率密度分布');
xlim([1,500]);
xlabel('里程(Km)');
ylabel('概率密度');
subplot(2,2,2)
plot(1:500,y2(1:500),'r-','Linewidth',1.5);
xlim([1,500]);
title('电动车日行驶里程概率累计分布');
xlabel('里程(Km)');
ylabel('累计概率');
subplot(2,2,3)
plot(1:N,y3_MC,'x');
title('MC随机抽样里程');
xlim([1,N]);
xlabel('车辆数');
ylabel('里程(km)');
subplot(2,2,4)
plot(1:N,y3_LHS,'x');
title('LHS随机抽样里程');
xlim([1,N]);
xlabel('车辆数');
ylabel('里程(km)');
end函数Time_In
%% 电动车起始充电时间采样
function [y3_MC,y3_lhs]=Time_In(N)
% 电动车起始充电时间概率分布(服从正态分布)
mu=17.6; % 均值
sigma=3.4; % 方差
%% 计算起始充电时间 概率分布
for t=1:24
if t>mu-12 && t<24
y1(t)=normpdf(t,mu,sigma);
else
y1(t)=normpdf(t+24,mu,sigma);
end
end
%% 计算起始充电时间 累积分布
y2= cumsum(y1) * 1;
%% MC抽样
p_MC=rand(N,1);
t=1:24;
for i=1:N
[~,idt] = min(abs(y2-p_MC(i,1)));
y3_MC(i) = t(idt);
end
%% LHS抽样
for i=1:N
node_max(i)=i/N;
node_min(i)=(i-1)/N;
end
p_lhs=(node_max'-node_min').*rand(N,1)+node_min'; % 变换
p_lhs=p_lhs(randperm(N));
t=1:24;
for i=1:N
[~,idt] = min(abs(y2-p_lhs(i,1)));
y3_lhs(i) = t(idt);
end
%% 绘图
figure('name','电动车充电起始时间');
subplot(2,2,1)
plot(1:24,y1,'r-','Linewidth',1.5);
title('电动车充电起始时间概率密度分布');
xlim([1,24]);
xticks([1,4,8,12,16,20,24]);
xlabel('时间(h)');
ylabel('概率密度');
subplot(2,2,2)
plot(1:24,y2,'r-','Linewidth',1.5);
title('电动车充电起始时间概率累计分布');
xlim([1,24]);
xticks([1,4,8,12,16,20,24]);
xlabel('时间(h)');
ylabel('累计概率');
subplot(2,2,3)
plot(1:N,y3_MC,'x');
title('MC法电动车充电起始时间');
xlim([1,N]);
xlabel('车辆数');
ylabel('起始充电时间(h)');
subplot(2,2,4)
plot(1:N,y3_lhs,'x');
title('LHS法电动车充电起始时间');
xlim([1,N]);
xlabel('车辆数');
ylabel('起始充电时间(h)');
end