并查集(Union-Find)算法全面详解
一、前言
在看一个算法题时,其中一种解法用到了并查集,并查集在《算法第四版——1.5案例研究: union-find 算法》中有讲解,这里按照自己的理解记录一下并查集。
二、用途
并查集用于判断连个点所在的集合是否属于同一个集合,若属于同一个集合但还未合并则将两个集合进行合并。同一个集合的意思是这两个点是连通的,直接相连或者通过其它点连通。
三、什么是并查集
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,用并查集来描述可以很好的解决这类问题。并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。在处理并查集的时候需要用到动态连通性概念,那什么是动态连通性呢?
3.1 动态连通性
首先我们详细地说明一下问题:问题的输入是一列整数对,其中每个整数都表示一个某种类型的对象,一对整数pq可以被理解为"p和a是相连的"。我们假设“相连”是一种等价关系,这也就意味着它具有:
- 自反性:p和p是相连的;
- 对称性:如果p和q是相连的,那么q和p也是相连的;
- 传递性:如果p和q是相连的且q和r是相连的,那么p和r也是相连的。
等价关系能够将对象分为多个等价类。在这里,当且仅当两个对象相连时它们才属于同一个等价类。我们的目标是编写一个程序来过滤掉序列中所有无意义的整数对(两个整数均来自于同一个等价类中)。换句话说,当程序从输入中读取了整数对p q时,如果已知的所有整数对都不能说明p和q是相连的,那么则将这一对整数写入到输出中。如果已知的数据可以说明p和q是相连的,那么程序应该忽略pq这对整数并继续处理输入中的下一对整数。图1.5.1用一个例子说明了这个过程。为了达到所期望的效果,我们需要设计一个数据结构来保存程序已知的所有整数对的足够多的信息,并用它们来判断一对新对象是否是相连的。我们将这个问题通俗地叫做动态连通性问题。这个问题可能有以下应用。
3.1.1 网络
输入中的整数表示的可能是一个大型计算机网络中的计算机,而整数对则表示网络中的连接。这个程序能够判定我们是否需要在p和q之间架设一条新的连接才能进行通信,或是我们可以通过已有的连接在两者之间建立通信线路;或者这些整数表示的可能是电子电路中的触点,而整数对表示的是连接触点之间的电路;或者这些整数表示的可能是社交网络中的人,而整数对表示的是朋友关系。在此类应用中,我们可能需要处理数百万的对象和数十亿的连接。
3.1.2 变量名等价性
某些编程环境允许声明两个等价的变量名(指向同一个对象的多个引用)。在一系列这样的声明之后,系统需要能够判别两个给定的变量名是否等价。这种较早出现的应用(如FORTRAN语言)推动了我们即将讨论的算法的发展。
3.1.3 数学集合
在更高的抽象层次上,可以将输入的所有整数看做属于不同的数学集合。在处理一个整数对pq时,我们是在判断它们是否属于相同的集合。如果不是,我们会将p所属的集合和a所属的集合归并到同一个集合。
为了进一步限定话题,我们会在本节以下内容中使用网络方面的术语,将对象称为触点,将整数对称为连接,将等价类称为连通分量或是简称分量。简单起见,假设我们有用0到N-1的整数所表示的N个触点。
四、API
为了说明问题,我们设计了一份API来封装所需的基本操作:初始化、连接两个触点、判断包含某个触点的分量、判断两个触点是否存在于同一个分量之中以及返回所有分量的数量。详细的API如表1.5.1所示。
如果两个触点在不同的分量中,union()操作会将两个分量归并。find()操作会返回给定触点所在的连通分量的标识符。connected()操作能够判断两个触点是否存在于同一个分量之中。count()方法会返回所有连通分量的数量。一开始我们有N个分量,将两个分量归并的每次union()操作都会使分量总数减一。
我们马上就将看到,为解决动态连通性问题设计算法的任务转化为了实现这份API。所有的实现都应该:
- 定义一种数据结构表示已知的连接;
- 基于此数据结构实现高效的union()、find()、 connected()和count()方法
众所周知,数据结构的性质将直接影响到算法的效率,因此数据结构和算法的设计是紧密相关的。API已经说明触点和分量都会用int值表示,所以我们可以用一个以触点为索引的数组id[]作为基本数据结构来表示所有分量。我们将使用分量中的某个触点的名称作为分量的标识符,因此你可以认为每个分量都是由它的触点之一所表示的。一开始,我们有N个分量,每个触点都构成了一个只含有它自己的分量,因此我们将id[i]的值初始化为i,其中i在0到N-1之间。对于每个触点i,我们将find()方法用来判定它所在的分量所需的信息保存在id[i]之中。connected()方法的实现只用一条语句find(p) == find(g),它返回一个布尔值,我们在所有方法的实现中都会用到connected()方法。
总之,我们维护了两个实例变量,一个是连通分量的个数,一个是数组id[],find()和union()的实现是剩余内容将要讨论的主题。
五 实现
我们将讨论三种不同的实现,它们均根据以触点为索引的id[]数组来确定两个触点是否存在于相同的连通分量中。
5.1 quick-find 算法
保证当且仅当id[p]等于id[q]时p和q是连通的。换句话说,在同一个连通分量中的所有触点在id[]中的值必须全部相同。这意味着connected(p,q)只需要判断id[p] ==id[q],当且仅当p和q在同一连通分量中该语句才会返回true。为了调用union (p,q)确保这一点,我们首先要检查它们是否已经存在于同一个连通分量之中。如果是我们就不需要采取任何行动,否则我们面对的情况就是p所在的连通分量中的所有触点的id[]值均为同一个值,而q所在的连通分量中的所有触点的id[]值均为另一个值。要将两个分量合二为一,我们必须将两个集合中所有触点所对应的id[]元素变为同一个值。如表1.5.2所示。为此,我们需要遍历整个数组,将所有和id [p]相等的元素的值变为id[q]的值。我们也可以将所有和id[q]相等的元素的值变为id[p]的值——两者皆可。根据上述文字得到的find()和union()的代码简单明了,如下面的代码框所示。图1.5.3显示的是我们的开发用例在处理测试数据tinyUF.txt时的完整轨迹。
5.1.1 quick-find 算法分析
find()操作的速度显然是很快的,因为它只需要访问id[]数组一次。但quick-find算法一般无法处理大型问题,因为对于每一对输入union()都需要扫描整个id[]数组。
5.2 quick-union 算法
quick-union 算法的重点是提高union()方法的速度,它和quick-find算法是互补的。它也基于相同的数据结构——以触点作为索引的id[]数组。每个触点所对应的id[]元素都是同一个分量中的另一个触点的名称(也可能是它自己)——我们将这种联系称为链接。在实现find()方法时,我们从给定的触点开始,由它的链接得到另一个触点,再由这个触点的链接到达第三个触点,如此继续跟随着链接直到到达一个根触点,即链接指向自己的触点。当且仅当分别由两个触点开始的这个过程到达了同一个根触点时它们存在于同一个连通分量之中。为了保证这个过程的有效性,我们需要union(p, q)来保证这一点。它的实现很简单:我们由p和q的链接分别找到它们的根触点,然后只需将一个根触点链接到另一个即可将一个分量重命名为另一个分量,因此这个算法叫做quick-union。和刚才一样,无论是重命名含有p的分量还是重命名含有q的分量都可以。图1.5.5显示了quick-union算法在处理tinyUF.txt时的轨迹。图1.5.4能够很好地说明图1.5.5(见1.5.2.4节)中的轨迹,我们接下来要讨论的就是它。
5.2.1 quick-union 算法分析
quick-union算法看起来比quick-find算法更快,因为它不需要为每对输入遍历整个数组。但它能够快多少呢?分析quick-union算法的成本比分析quick-find算法的成本更困难,因为这依赖于输人的特点。在最好的情况下,find()只需要访问数组一次就能够得到一个触点所在的分量的标识符;而在最坏情况下,这需要N-1次数组访问。我们可以将quick-union算法看做是quick-find算法的一种改良,因为它解决了quick-find算法中最主要的问题(union()操作总是线性级别的)。对于一般的输入数据这个变化显然是一次改进,但quick-union算法仍然存在问题,我们不能保证在所有情况下它都能比quick-find算法快得多(对于某些输人,quick-union算法并不比quick-find算法快)。
5.3 加权quick-union 算法
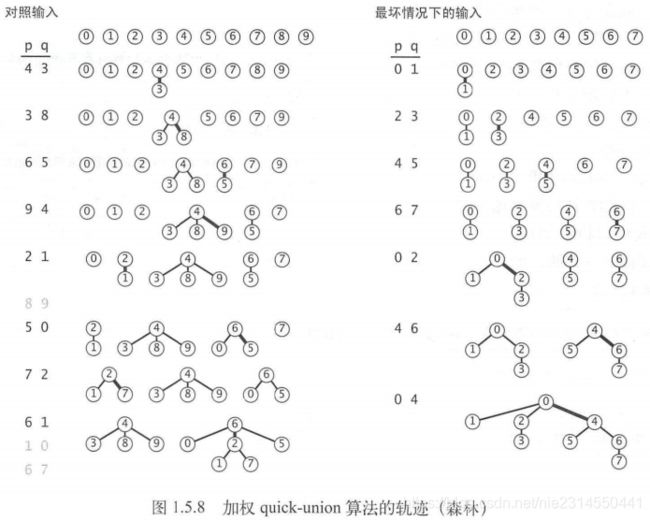
我们现在会记录每一棵树的大小并总是将较小的树连接到较大的树上。这项改动需要添加一个数组和一些代码来记录树中的节点数,它能够大大改进算法的效率。我们将它称为加权quick-union算法(如图1.5.7所示)。该算法在处理tinyUF.txt时构造的森林如图1.5.8中左侧的图所示。即使对于这个较小的例子,该算法构造的树的高度也远远小于未加权的版本所构造的树的高度。
5.3.1 加权quick-unio 算法
图1.5.8显示了加权quick-union算法的最坏情况。其中将要被归并的树的大小总是相等的(且总是2的幂)。这些树的结构看起来很复杂,但它们均含有2^2个节点,因此高度都正好是n。另外,当我们归并两个含有2^2个节点的树时,我们得到的树含有2^(2+1)个节点,由此将树的高度增加到了n+1。由此推广我们可以证明加权quick-union算法能够保证对数级别的性能。加权quick-union算法的实现如算法1.5所示。
六、三种算法特点
七、展望——《算法第四版1.5.3》
- 完整而详细地定义问题,找出解决问题所必需的基本抽象操作并定义一份API
- 简洁地实现一种初级算法,给出一个精心组织的开发用例并使用实际数据作为输入
- 当实现所能解决的问题的最大规模达不到期望时决定改进还是放弃。
- 逐步改进实现,通过经验性分析或(和)数学分析验证改进后的效果。
- 用更高层次的抽象表示数据结构或算法来设计更高级的改进版本。
- 如果可能尽量为最坏情况下的性能提供保证,但在处理普通数据时也要有良好的性能。
- 在适当的时候将更细致的深入研究留给有经验的研究者并继续解决下一个问题。
八、感想
先看了一道算法题解答中用到了并查集,然后再看并查集,导致自己在看并查集的时候脑子里一直盘旋的是那道算法题,在看并查集的时候一直在想怎样用并查集更好的解决那道算法题,以至于忽略了并查集算法本身需要解决的问题。期间还在想p和q之间路径能不能找到。
在看一个已经定于好算法时,需要专注的是这个算法本身,问题扩展应该是在理解当前算法之后。《算法第四版1.5.3》其中有一条说道——完整而详细地定义问题。
九、编码实现
//==========================================================================
/**
* @file : 01_UnionFind.h
* @blogs : https://blog.csdn.net/nie2314550441/article/details/106954784
* @author : niebingyu
* @title : 并查集
* @purpose : 并查集用于判断连个点所在的集合是否属于同一个集合,
* 若属于同一个集合但还未合并则将两个集合进行合并。
*
*/
//==========================================================================
#pragma once
#include
#include
#include
#include
using namespace std;
#define NAMESPACE_UNIONFIND namespace NAME_UNIONFIND {
#define NAMESPACE_UNIONFINDEND }
NAMESPACE_UNIONFIND
// 方法一 quick-find
class UF
{
public:
UF(int N)
{
if (N < 0) return;
m_count = N;
m_arr.resize(N);
for (int i = 0; i < N; ++i)
{
m_arr[i] = i;
}
}
// p(0 到 N-1)所在的分量的标识符
int find(int p)
{
if (p < 0 || p >= m_arr.size())
return -1;
return m_arr[p];
}
// 在 p 和 q 之间添加一条连续
void Union(int p, int q)
{
int pID = find(p);
int qID = find(q);
if (pID == qID)
return;
for (int i = 0; i < m_arr.size(); ++i)
{
if (m_arr[i] == pID)
m_arr[i] = qID;
}
--m_count;
}
// 如果 p 和 q 存在于同一个分量中则返回 true
bool connected(int p, int q)
{
return find(p) == find(q);
}
// 连通分量的数量
int count()
{
return m_count;
}
private:
int m_count; // 风量数量
vector m_arr; // 分量id(以触点作为索引)
};
// 方法二 quick-union
class QF
{
public:
QF(int N)
{
if (N < 0) return;
m_count = N;
m_arr.resize(N);
for (int i = 0; i < N; ++i)
{
m_arr[i] = i;
}
}
// p(0 到 N-1)所在的分量的标识符
int find(int p)
{
if (p < 0 || p >= m_arr.size())
return -1;
while (p != m_arr[p])
{
p = m_arr[p];
}
return p;
}
// 在 p 和 q 之间添加一条连续
void Union(int p, int q)
{
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot)
return;
m_arr[pRoot] = qRoot;
--m_count;
}
// 如果 p 和 q 存在于同一个分量中则返回 true
bool connected(int p, int q)
{
return find(p) == find(q);
}
// 连通分量的数量
int count()
{
return m_count;
}
private:
int m_count; // 风量数量
vector m_arr; // 分量id(以触点作为索引)
};
// 方法三 加权quick-union
class WeightedQuickUnionUF
{
public:
WeightedQuickUnionUF(int N)
{
m_count = N;
m_id.resize(N);
m_sz.resize(N);
for (int i = 0; i < N; ++i)
{
m_id[i] = i;
m_sz[i] = i;
}
}
// p(0 到 N-1)所在的分量的标识符
int find(int p)
{
if (p < 0 || p >= m_id.size())
return -1;
while (p != m_id[p])
{
p = m_id[p];
}
return p;
}
// 在 p 和 q 之间添加一条连续
void Union(int p, int q)
{
int pi = find(p);
int qi = find(q);
if (pi == qi)
return;
if (m_sz[pi] < m_sz[qi])
{
m_id[pi] = qi;
m_sz[qi] += m_sz[pi];
}
else
{
m_id[qi] = pi;
m_sz[pi] += m_sz[qi];
}
--m_count;
}
// 如果 p 和 q 存在于同一个分量中则返回 true
bool connected(int p, int q)
{
return find(p) == find(q);
}
// 连通分量的数量
int count()
{
return m_count;
}
private:
vector m_id; // 父链接数组(由触点索引)
vector m_sz; // (由触点索引的)各个根节点所对应的风量的大小
int m_count; // 连通分量的数量
};
//
// 测试 用例 START
struct PQ
{
int p, q;
PQ(int pi, int qi) :p(pi), q(qi) {}
};
void test(const char* testName, vector nums, int count)
{
//UF S(10);
//QF S(10);
WeightedQuickUnionUF S(10);
for (int i = 0; i < nums.size(); ++i)
{
S.Union(nums[i].p, nums[i].q);
}
// 粗略校验
if (S.count() == count)
cout << testName << ", solution passed." << endl;
else
cout << testName << ", solution failed. S.count():" << S.count() << " ,count:" << count << endl;
}
// 测试用例
void Test1()
{
vector gArr = { PQ(4,3), PQ(3,8), PQ(6,5), PQ(9,4), PQ(2,1), PQ(8,9), PQ(5,0), PQ(7,2), PQ(6,1), PQ(1,0), PQ(6,7) };
int expect = 2;
test("Test1()", gArr, expect);
}
NAMESPACE_UNIONFINDEND
// 测试 用例 END
//
void UnionFind_Test()
{
NAME_UNIONFIND::Test1();
} 执行结果:
![]()