<蓝桥杯软件赛>零基础备赛20周--第12周--DFS基础(必考)
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上答疑:929486294
文章目录
- 1. 搜索概述
- 2. DFS概述
-
- 2.1 DFS的代码框架
- 3. DFS与排列
-
- 3.1 输出全排列
- 3.2 输出部分排列
- 4. DFS与组合
- 5. DFS与连通性
- 6. DFS例题
-
- N皇后
- 与或异或
- 有奖问答
- 飞机降落
- 最大数字
- 买瓜
- 7. 习题
第12周: DFS
如果问蓝桥杯一定会考什么,绝对不会缺席的那种,答案肯定是:DFS!
例如2023年蓝桥杯省赛,有8道题和DFS有关,或者直接用DFS,或者基于DFS的高级算法:有奖问答、分糖果、飞机降落、与或异或、树上选点、异或和、景区导游、像素放置。
1. 搜索概述
有人说,只要学通了搜索,在蓝桥杯省赛上就能稳得二等奖。这个说法有开玩笑的意思,其实他的重点是强调搜索的重要性。
为什么搜索这么重要?因为搜索是“暴力法”的具体实现,暴力法是最直接、最充分利用计算机强大算力的方法。竞赛题目很多可以用暴力法做,即使暴力法的效率不高,在蓝桥杯这样的赛制中,也可能通过部分测试,得到一些分数。
什么是暴力法?一道算法题,给定输入,有对应的输出。自然地会有一种最简单的解题方法:把所有可能的情况都罗列出来,然后逐一检查,根据给定的输入找到对应的输出,从而得到答案。这种方法称为暴力法(Brute force)。
虽然所有问题都能用暴力法来求解,但暴力法也往往是“低效”的代名词。暴力法虽然低效,但优点是简单,相对其他“高效”算法,暴力法的代码一般都更短、更好写。在蓝桥杯大赛中,当拿到一个题目后,如果没有更好的思路,可以考虑用暴力法,通过一部分测试,拿到部分分数,这是蓝桥杯大赛的必备技能。
暴力法的主要手段之一是搜索。很多情况下,如果不会写搜索的代码,那么连暴力法都实现不了。这是为什么搜索如此重要的原因。
搜索包括两种基本技术:宽度优先搜索(BFS,Breadth-First Search)、深度优先搜索(DFS,Depth-First Search)。它们是算法竞赛常见的知识点,DFS尤其常见,是蓝桥杯考核最多的知识点。
下面以老鼠走迷宫为例说明BFS和DFS的原理。
给定一个迷宫,迷宫内道路错综复杂,老鼠从入口进去后,如何找到出口?由于老鼠对迷宫一无所知,它只能暴力地搜索所有可能的道路,直到找到一个出口。
有两种走迷宫方案,它们分别体现了BFS和DFS的原理。
(1)一只老鼠走迷宫。它在每个路口,都选择先走右边(或者都选择先走左边),能走多远就走多远;直到碰壁无法再继续往前走,然后往回退一步,这一次走左边,然后继续往下走。用这个办法,只要没遇到出口,就会走遍所有的路,而且不会重复,这里规定回退不算重复走(即使算重复走,也只多走一次)。这个方法就是DFS,概况DFS的思路:一路到底、逐步回退。
(2)一群老鼠走迷宫。假设老鼠无限多,这群老鼠进去后,在每个路口,都派出部分老鼠探索所有没走过的路。走某条路的老鼠,如果碰壁无法前行,就停下;如果到达的路口已经有别的老鼠探索过了,也停下。很显然,在遇到出口前,所有的道路都会走到,而且不会重复。这个方法就是BFS,概况BFS的思路:全面扩散,逐层递进。
BFS和DFS的计算量是多少?对迷宫问题来说,计算量体现在它们在迷宫内部走了多少路口和边。显然不管是BFS和DFS,每个路口和边,它们都只走一次。设路口有n个,边有m条,计算量是O(n+m)。概括地说,BFS和DFS都能找到出口,且都需要暴力搜到所有的路口和道路,它们的计算量是一样的。
DFS的优势:DFS能搜索并输出从入口到出口的所有路径,BFS不行。从入口到出口的路径数量极多,例如一个十几个路口,几十条边的迷宫,路径可能多达数万。一般不会要求输出路径,或输出路径的数量。
BFS的优势:BFS能快速找到最短路径,DFS很困难。为什么BFS能快速找到最短路径?以某个路口为例,当有老鼠第一次到达这个路口时,这只老鼠走过的路径一定是最短路径。因为如果是兜圈子过来的,这只老鼠就不是第一个到了。BFS搜最短路径,计算量是O(n+m)的。在算法竞赛中,用BFS求最短路径是常见考点。如果用DFS求最短路径,只能先搜出所有路径,再比较得到最短的。由于路径数量极多,所以计算量极大。
编码时,BFS需要用队列这种数据结构来实现,“BFS = 队列”;DFS用递归实现,“DFS = 递归”。DFS的编码比BFS的编码简单一些。
2. DFS概述
DFS是算法竞赛的必考知识点,在任何一场算法竞赛中都不会缺席。
(1)知识点:DFS是必学的基础算法,是暴力技术的体现。
(2)编码:DFS的编码很有技巧性,能很好地考验编码能力。
(3)扩展:DFS是很多高级算法的基础。
(4)应用:DFS的应用很广,题目可难可易。
2023年的蓝桥杯省赛,有三道纯DFS题(有奖问答、与或异或、分糖果,仅仅只用到DFS,没有用到其他知识点)是作为填空题出现的,一题仅有5分。这说明出题人认为DFS是必须掌握的基础知识点,一道纯DFS题只能给5分。这一年还有多道大题用到DFS,但是需要结合其他算法。
2.1 DFS的代码框架
下面给出DFS的代码框架,DFS用递归实现。
ans; //答案,常常用全局变量表示
void dfs(层数,其他参数){
if (到达目的地、或者出局){ //到达最底层,或者满足条件退出
更新答案ans; //答案一般用全局变量表示,ans是最优解
return; //递归返回,即返回到上一层
}
(剪枝) //在进一步DFS之前剪枝
for (用i遍历下一层所有可能的情况) //对每一个情况继续DFS
if (used[i] == 0) { //如果状态i没有处理过,就可以进入下一层dfs
used[i] = 1; //标记状态i为已经使用,在后续dfs时不能再使用
dfs(层数+1,其他参数); //下一层,即搜小规模后继续dfs
used[i] = 0; //恢复状态i,回溯时,不影响上一层对这个状态的使用
}
return; //返回到上一层
}
代码看起来不长,但是对初学者来说还是有学习难度。在DFS框架中,最让初学者费解的是第10行和第12行,它们是对递归的理解。
第10行的used[i] = 1,称为“保存现场”,或“占有现场”。
第12行的used[i] = 0,称为“恢复现场”,或“释放现场”。
请读者在大量编码的基础上,再回头体会这个框架的作用。
DFS常见的应用场景有:排列组合、连通性。
3. DFS与排列
3.1 输出全排列
本节从DFS的一个基础应用开始:生成排列。排列问题在蓝桥杯题目中常常出现。
全排列问题是典型的“暴力”问题,n个数的全排列,共有n!种,在每个排列中,每个数出现一次,而且只出现一次。
例题 全排列问题
如果n比较小,可以写n个for循环输出全排列。但是这种简单方法只能用于较小的n,如果n比较大,这种方法的代码非常冗长、难看。
DFS非常适合实现全排列,代码清晰、简洁、优美。下面的C++代码能从小到大打印排列。
#include 代码用b[1]~b[n]记录一个全排列。下面以n=3为例,图解代码的执行过程。圆圈内的数字是全排列的数字,例如最上面一行生成的排列是{1, 2, 3}。一共生成6个全排列。用下面的图解释DFS生成全排列的过程。
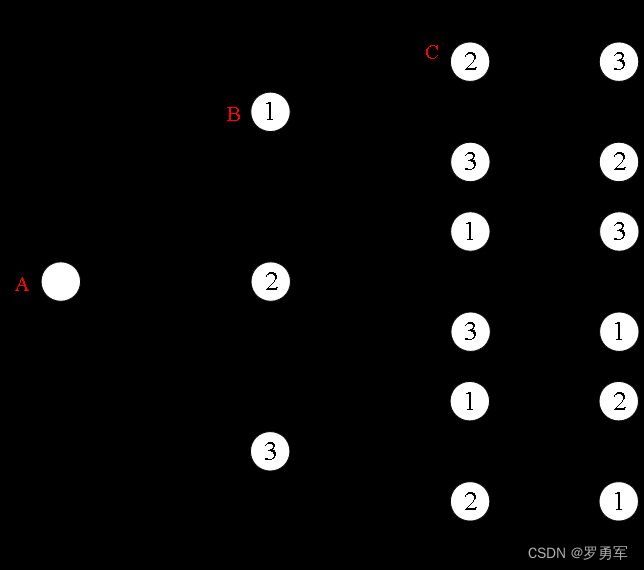
代码第27行从dfs(1)开始,这是第一次进入dfs()。图中相关的是标注A的位置。第14行进入for循环,在第16行赋值:i=1时b[1]=1;i=2时b[1]=2;i=3时b[1]=3。对应图中最左边三条线上标注的i=1、i=2、i=3。
i=1时,在17行vis[1]=1,表示a[1]=1已经放在排列中,后续不能再用。然后进入dfs(2),这是第二次进入dfs()。图中相关的是标注B的位置。
dfs(2)时,第14行进入for循环。当i=1时,第15行判断vis[1]已经被使用,所以不再继续,用图中最上面的虚线表示i=1不再继续。i=2和i=3可以继续往后执行,例如i=2时,先赋值b[2]=2;然后进入dfs(3),并赋值b[3]=3;最后进入dfs(4),在第8行判断已经得到全排列,输出第一个全排列{1, 2, 3}。图中相关的是标注C的位置。
后续过程,读者可以继续模拟。特别注意第17行vis[i]=1和第19行vis[i]=0的作用。
Java代码。
import java.util.Scanner;
public class Main {
static int n;
static boolean[] vis;
static int[] a;
static int[] b;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
vis = new boolean[10];
a = new int[10];
b = new int[10];
for (int i = 1; i <= n; i++) a[i] = i;
dfs(1);
}
static void dfs(int step) {
if (step == n + 1) {
for (int i = 1; i <= n; i++)
System.out.printf("%5d", b[i]);
System.out.println();
return;
}
for (int i = 1; i <= n; i++) {
if (vis[i] == false) {
b[step] = a[i];
vis[i] = true;
dfs(step + 1);
vis[i] = false;
}
}
}
}
Python代码。
n = int(input())
vis = [0] * 10
a = [0] * 10
b = [0] * 10
def dfs(step):
if step == n + 1:
for i in range(1, n+1):
print("%5d" %b[i], end="")
print()
return
for i in range(1, n+1):
if vis[i] == 0:
b[step] = a[i]
vis[i] = 1
dfs(step + 1)
vis[i] = 0
for i in range(1, n+1): a[i] = i
dfs(1)
3.2 输出部分排列
上述代码是打印n个数的全排列,如果需要打印n个数中任意m个数的排列,略作修改即可。例如n=4,m=3,修改C++代码这两处:第8行把step=n+1改为step=m+1,第9行i<=n改为i<=m。
4. DFS与组合
如果要打印n个数中m个数的组合,同样可以用DFS。
DFS时,选或不选第k个数,就实现了各种组合。下面举两个例子。
(1)输出二进制。以打印000 ~ 111为例,下面是Python代码,C++和Java略。
vis = [0]*10
def dfs(k): #深搜到第k个数
if k == 4: #已经得到3个数的组合
for i in range (1,4): print(vis[i],end='')
print(' ',end='')
else:
vis[k] = 0 #第k个选数字0,或者理解为第k个不选(0表示不选)
dfs(k + 1) #继续搜下一个
vis[k] = 1 #第k个选数字1,或者理解为第k个选中(1表示选中)
dfs(k + 1) #继续搜下一个
dfs(1)
输出:000 001 010 011 100 101 110 111
如果要反过来,只需要交换7、9行,输出:111 110 101 100 011 010 001 000
(2)输出组合。以包含3个元素的集合{a, b,c}为例,输出它所有的子集。
下面是Python代码,C++和Java略。代码输出: c b bc a ac ab abc
a = [' ', 'a', 'b', 'c']
vis = [0] * 10
def dfs(k):
if k == 4:
for i in range(1, 4):
if vis[i]: print(a[i], end='')
print(' ', end='')
else:
vis[k] = 0 #不选中第k个元素
dfs(k + 1) #继续搜下一个元素
vis[k] = 1 #选第k个元素
dfs(k + 1) #继续搜下一个元素
dfs(1)
5. DFS与连通性
连通性判断是DFS最常见的应用。连通性判断是图论中的一个简单问题,给定一张图,图由点和边组成,要求找到互相连通的部分。连通性判断有三种实现方法:BFS、DFS、并查集,用DFS最简单方便。
在竞赛题中,图常常用方格图给出,每个方格可以向上下左右四个方向走。
DFS判断连通性,步骤如下:
(1)从任意一个点u开始遍历,标记u已经搜过。一般从第一个点开始。
(2)DFS搜索u的所有符合连通条件的邻居点。已经搜过的点标记为已经搜过,后面不用再搜。扩展u的邻居点时,应该判断这个邻居点是不是在边界内。
(3)DFS结束,找到了与u连通的所有点,这是一个连通块。
(4)不与u连通的、其他没有访问到的点,继续用上述步骤处理,找到所有的连通块。
DFS搜连通的计算复杂度如何?因为每个点只用搜一次且必须至少搜一次,共N个点,DFS的复杂度是O(N)的,不可能更好了。
例题 最大连通
C++代码。
#includejava代码
import java.util.Scanner;
public class Main {
static int[] dx = {-1, 0, 1, 0};
static int[] dy = {0, 1, 0, -1};
static char[][] g;
static int n = 30, m = 60;
static int dfs(int x, int y) {
if (g[x][y] == '0') return 0;
g[x][y] = '0';
int cnt = 1;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue;
cnt += dfs(nx, ny);
}
return cnt;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
g = new char[n][m];
for (int i = 0; i < n; i++) g[i] = scanner.nextLine().toCharArray();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (g[i][j] == '1')
ans = Math.max(ans, dfs(i, j));
System.out.println(ans);
}
}
python代码
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
n,m = 30,60
def dfs(x, y):
if g[x][y] == '0': return 0
g[x][y] = '0'
cnt = 1
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or ny < 0 or nx >= n or ny >= m: continue
cnt += dfs(nx, ny)
return cnt
g = list()
for i in range(30): g.append(list(input().strip()))
ans = 0
for i in range(n):
for j in range(m):
if g[i][j] == '1':
ans = max(ans, dfs(i, j))
print(ans)
例题 全球变暖
这是典型的连通性问题,计算步骤是:遍历一个连通块(找到这个连通块中所有的’#‘,并标记已经搜过,不用再搜);再遍历下一个连通块……;遍历完所有连通块,统计有多少个连通块。
什么岛屿不会被完全淹没?若岛中有个陆地(称为高地),它周围都是陆地,那么这个岛不会被完全淹没。用DFS搜出有多少个岛(连通块),检查这个岛有没有高地,统计那些没有高地的岛(连通块)的数量,就是答案。
C++代码。
#includeJava代码
import java.util.Scanner;
public class Main {
static char[][] mp;
static int[][] vis;
static int[][] d = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
static int flag;
static void dfs(int x, int y) {
vis[x][y] = 1;
if (mp[x][y + 1]=='#' && mp[x][y-1]=='#' && mp[x+1][y]=='#' && mp[x-1][y]=='#')
flag = 1;
for (int i = 0; i < 4; i++) {
int nx = x + d[i][0], ny = y + d[i][1];
if (nx>=0 && ny>=0 && nx<mp.length && ny<mp[0].length && vis[nx][ny]==0 && mp[nx][ny] == '#')
dfs(nx, ny);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
mp = new char[n][n];
vis = new int[n][n];
for (int i = 0; i < n; i++) mp[i] = scanner.next().toCharArray();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (mp[i][j] == '#' && vis[i][j] == 0) {
flag = 0;
dfs(i, j);
if (flag == 0) ans++;
}
System.out.println(ans);
}
}
Python代码。需要在第2行用setrecursionlimit()设置递归深度,否则不能通过100%的测试。
import sys
sys.setrecursionlimit(60000) #设置递归深度
def dfs(x,y):
d = [(0,1),(0,-1),(1,0),(-1,0)]
global flag
global vis
global mp
vis[x][y] = 1
if mp[x][y+1]=='#' and mp[x][y-1]=='#' and mp[x+1][y]=='#' and mp[x-1][y]=='#':
flag = 1
for i in range(4):
nx = x+d[i][0]
ny = y+d[i][1]
if vis[nx][ny]==0 and mp[nx][ny]=='#': dfs(nx,ny)
n = int(input())
mp =[]
for i in range(n): mp.append(list(input()))
vis = []
for i in range(n): vis.append([0]*n)
ans = 0
for i in range(n):
for j in range(n):
if vis[i][j]==0 and mp[i][j]=='#':
flag = 0
dfs(i,j)
if flag == 0: ans+=1
print(ans)
6. DFS例题
N皇后
链接 N皇后
n皇后问题是DFS的经典应用。把n个皇后放在棋盘上,要求不同列、不同行、不在同一条对角线。只能用暴力法尝试所有可能的方案,去掉非法方案,得到合法方案。这实际是排列问题,用DFS搜索所有排列最方便。
题目还要求输出3种方案,而且是字典序的前3种方案。这不难实现,只要按行从1到n、列从1到n的顺序尝试放皇后的方案即可。得到的合法方案,就是字典序的。
本题的主要技巧是如何判断同行、同列、同对角线上是否已经有其他皇后。
设当前处理到第x行,前1 ~ x-1行已经放好了皇后。由于一行只放一个皇后,所以两个皇后同行的冲突情况不用再判断,只需要判断同列、同对角线的情况,对角线又分为主对角线、副对角线。下图中三根虚线,vis是同列,vis1是主对角线,vis2是副对角线。

同列vis上的点有什么特征?它们的y坐标相同。用数组vis[]表示列,vis[y]=1表示第y列已经放了皇后。
主对角线vis1上的点有什么特征?观察上图,沿着主对角线vis1走一步,x坐标加1,y坐标减一,那么x+y不变。也就是说,一条vis1线上的所有点的x+y都相等。例如一条主对角线上的点[1, 5]、[2, 4]、[3, 3]、[4, 2]、[5,1],都有x+y=6。用数组vis1[]表示主对角线,vis1[x+y]=1表示坐标[x, y]所在的主对角线上已经有皇后。
副对角线vis2上的点有什么特征?沿着副对角线vis2走一步,x和y坐标都加1,那么x-y不变。例如一条副对角线上的点[1, 3]、[2, 4]、[3, 5]、[4, 6],都有x-y=-2。用数组vis2[]表示副对角线,vis2[x-y+n]=1表示坐标[x, y]所在的副对角线上已经有皇后。这里不能直接用x-y,因为它可能为负数,加上n后就变成了正数。n也可以改为一个大于n的数k,只要保证x-y+k>0就行,不过要记得把vis2[]开大一些,防止溢出。
除了以上技巧,代码的其他部分就是常见的DFS求排列。
C++代码。
#includejava
import java.util.Scanner;
public class Main {
static int n, tot; //n: 行数; tot:方案数
static int[] ans; //ans[x]: 第x行皇后放在第几列
static int[] vis; //vis[y]=1: 第y列放了皇后
static int[] vis1; //vis1[x+y]=1: 主对角线放了皇后
static int[] vis2; //vis2[x-y+n]=1: 副对角线放了皇后
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
ans = new int[n + 1];
vis = new int[n + 1];
vis1 = new int[2 * n + 1];
vis2 = new int[2 * n + 1];
dfs(1);
System.out.println(tot);
}
static void dfs(int x) { //第x行,枚举所有列
if (x == n + 1) { //已经放完n行
tot++;
if (tot <= 3) {
for (int i = 1; i <= n; i++) System.out.print(ans[i] + " ");
System.out.println();
}
return;
}
for (int y = 1; y <= n; y++) { //枚举坐标(x, y)
if (vis[y] == 1) continue; //第y列已经有皇后
if (vis1[x+y] == 1) continue; //主对角线已经有皇后
if (vis2[x-y+n] == 1) continue; //副对角线已经有皇后
ans[x] = y;
vis[y] = 1; vis1[x+y] = 1; vis2[x-y+n] = 1; //保存现场
dfs(x + 1); //继续下一行
vis[y] = 0; vis1[x+y] = 0; vis2[x-y+n] = 0; //恢复现场
}
}
}
python
#pypy
n = int(input())
tot = 0 # tot:方案数
ans = [0] * 20 # ans[x]: 第x行皇后放在第几列
vis = [0] * 30 # vis[y]=1: 第y列放了皇后
vis1 = [0] * 30 # vis1[x+y]=1: 主对角线放了皇后
vis2 = [0] * 30 # vis2[x-y+n]=1: 副对角线放了皇后
def dfs(x):
global tot
if x == n+1: # 已经放完n行
tot += 1
if tot <= 3:
for i in range(1, n+1): print(ans[i], end=' ')
print()
return
for y in range(1, n+1): # 枚举第x行的坐标(x, y)
if vis[y] or vis1[x+y] or vis2[x-y+n]: continue
ans[x] = y
vis[y], vis1[x+y], vis2[x-y+n] = 1,1,1 # 保存现场
dfs(x + 1) # 继续下一行
vis[y], vis1[x+y], vis2[x-y+n] = 0,0,0 # 恢复现场
dfs(1)
print(tot)
与或异或
链接 与或异或
题目的思路很简单。10个逻辑门,每个逻辑门有与、或、异或三种选项,在这10个逻辑门的所有排列中(共 3 10 = 59049 3^{10}=59049 310=59049种),问有多少种排列的最后计算结果是1。
这一题是DFS求组合的简单应用。读者可以与前面DFS求组合的基本应用比较。
下面是C++代码。代码的计算量有多少?dfs()在第27行中继续做3次dfs(),一共有10个逻辑门,所以一共做了 3 10 = 59049 3^{10}=59049 310=59049次dfs。每次dfs在check()中做两重for循环约十几次。所以总计算量很小。
C++代码
#include 读者可能注意到,在dfs()中并没有做DFS常见的“保存现场、恢复现场”操作。因为10个逻辑门是相互独立的,每个逻辑门独立选“与、或、异或”,与其他逻辑门无关。而前面介绍的数字的全排列,一个数字被使用后,就不能放到其他位置,所以需要用“保存现场”占住它。
java代码
public class Main {
static int[][] a = new int[5][5]; //记录图中圆圈中的值
static int[] gate = new int[11]; //记录10个逻辑门的一种排列
static int ans; //答案
static int logic(int x, int y, int op) { //逻辑操作:c=1:与; c=2:或; c=3:异或
if(op == 1) return x & y; //与
if(op == 2) return x | y; //或
return x ^ y; //异或
}
static int check() { //检查10个逻辑门的排列,最后out是否为1
int op = 0;
a[0][0] = 1; a[0][1] = 0; a[0][2] = 1; a[0][3] = 0; a[0][4] = 1;
for(int i = 1; i <= 4; i++) //从上到下有4行逻辑门
for(int j = 0; j <= 4 - i; j++) //每一行从左到右
a[i][j] = logic(a[i-1][j], a[i-1][j+1], gate[op++]);
if(a[4][0] == 1) return 1; //out=1,结果正确
return 0;
}
static void dfs(int k) { //第k个逻辑门
if(k == 10) { //10个逻辑门都分配好了。下面模拟这一种组合方式
if(check() == 1) ans++; //out=1,结果正确
return;
}
for(int i = 1; i <= 3; i++) { //第k个逻辑门有三种选择:与、或、异或
gate[k] = i; //记录第k个逻辑门:与、或、异或
dfs(k + 1); //继续深搜第k+1个逻辑门
}
}
public static void main(String[] args) {
dfs(0);
System.out.println(ans);
}
}
python代码
a = [[0 for _ in range(5)] for _ in range(5)] #记录图中圆圈中的值
gate = [0] * 11 #记录10个逻辑门的一种排列
ans = 0 #答案
def logic(x, y, op): #逻辑操作:c=1:与; c=2:或; c=3:异或
if op == 1: return x & y #与
if op == 2: return x | y #或
return x ^ y #异或
def check(): #检查10个逻辑门,最后out是否为1
op = 0
a[0] = [1, 0, 1, 0, 1]
for i in range(1, 5): #从上到下有4行逻辑门
for j in range(0, 5 - i): #每一行从左到右
a[i][j] = logic(a[i-1][j], a[i-1][j+1], gate[op])
op += 1
if a[4][0] == 1: return 1 #out=1,结果正确
return 0
def dfs(k): #第k个逻辑门
global ans
if k == 10: #一共有10个逻辑门,现在都分配好了。下面模拟这一种组合方式
if check() == 1: ans += 1 #out=1,结果正确
return
for i in range(1, 4): #第k个逻辑门有三种选择:与、或、异或
gate[k] = i #记录第k个逻辑门:与、或、异或
dfs(k + 1) #继续深搜第k+1个逻辑门
dfs(0)
print(ans)
有奖问答
链接 有奖问答
这一题是C++组的填空题,填空题对运行时间要求不高,可以用比较耗时的算法做。
本题的正解是动态规划DP,计算量小,运行时间快。不过因为是填空题,可以用暴力方法做,即用DFS编码直接搜索所有情况。虽然DFS的计算量比DP大很多,但是思路简单,编码时间短。
下面是C++代码。dfs()模拟做题过程,思路直接。
C++
#include 代码的计算量有多大?第13、14行继续做2次dfs,计算复杂度是 O ( 2 n ) O(2^n) O(2n)。当n=30时,约十亿次,运行时间小于1分钟。
这一题出题人考核的就是DFS。故意让n=30,用DFS刚好能1分钟运行结束得到答案。如果n更大一些,运行时间就太长了,DFS就不合适了。
这一题不适合用python,因为python的循环很慢,运行时间极长。
飞机降落
链接 飞机降落
题目看起来似乎可以用贪心求解,请读者思考是否可行。
本题的N很小,计算量不大,可以求N架飞机的全排列,然后逐一验证验证每个全排列,如果有合法的一个全排列就打印YES,如果所有全排列都不合法就打印NO。
求全排列可以用库函数next_permutation()。本题给的时间限制是2秒,最多有10!个全排列,用next_permutation()的代码运行时间正好2秒,勉强通过测试。
next_permutation()的缺点是不能剪枝:必须先求得一个完整全排列,然后再判断这个全排列是否合法。而大部分全排列的前几项就已经不合法了,不用求完整的全排列。
本题更保险的方法是自己写DFS求全排列,可以在验证一个全排列时在中间剪枝,运行时间比next_permutation()短很多,仅有0.1秒。
C++代码。第12行剪枝,如果这架飞机安排不了就跳过它,相当于终止计算这个全排列。
#include java代码
import java.util.Scanner;
public class Main {
private static int[] T;
private static int[] D;
private static int[] L;
private static int n;
private static int[] vis;
private static int ans;
private static void dfs(int plane, int time) {
if(plane == n) {
ans = 1;
return;
}
for(int i = 0; i < n; i++) {
if(vis[i] == 0 && time <= T[i] + D[i]) {
int t = time;
if(t < T[i]) t = T[i];
vis[i] = 1;
dfs(plane + 1, t + L[i]);
vis[i] = 0;
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int m = scanner.nextInt();
while(m-- > 0) {
n = scanner.nextInt();
T = new int[n]; D = new int[n]; L = new int[n];
vis = new int[n];
for(int i = 0; i < n; i++) {
T[i] = scanner.nextInt();
D[i] = scanner.nextInt();
L[i] = scanner.nextInt();
}
ans = 0;
dfs(0, 0);
if(ans == 1) System.out.println("YES");
else System.out.println("NO");
}
}
}
python代码
def dfs(plane, time):
global ans
if plane == n:
ans = 1
return
for i in range(n):
if vis[i] == 0 and time <= T[i] + D[i]:
t = time
if t < T[i]: t = T[i]
vis[i] = 1
dfs(plane + 1, t + L[i])
vis[i] = 0
m = int(input())
for _ in range(m):
n = int(input())
T,D,L = [],[],[]
vis = []
for i in range(n):
t, d, l = map(int, input().split())
T.append(t)
D.append(d)
L.append(l)
vis.append(0)
ans = 0
dfs(0, 0)
if ans == 1: print("YES")
else: print("NO")
最大数字
链接 最大数字
要把N变成最大数字,可以用贪心思路依次处理N每一位:先把最高位尽量变成最大的数字,再把次高位尽量变成最大数字,…,等等。
首先明确一点,1号操作和2号操作不要混用,因为它们互相抵消,混用浪费。
如何把最高位尽量变大?设最高位的数字是d。
先试试1号操作,得到最大数字x,x最大能到9。取操作次数t = min(A, 9-d),其中9-d表示能得到9的次数;如果A次到不了9,就做A次。
再试试2号操作,因为是减1,所以只有能变成9才有意义。如果有B>d,那么可以减d+1次变成9。
其他位也这样处理,直到用完操作次数A和B。
以上过程可以直接模拟,见下面的Java代码。也可以用DFS来实现,见下面的C++和Python代码。
C++代码。dfs(i, v)的参数i表示当前处理到第i位,例如N=123,第一次dfs(0, 0),i=0表示第0位是1。dfs(i, v)的参数v是已经得到的值,例如第0位的数字1处理完后,1变成9,那么v=9。
#includeJava代码。直接模拟题意,不用DFS。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s=in.next(); //数字N按字符串读入
int A = in.nextInt();
int B = in.nextInt();
int[] a=new int[s.length()]; //把N的每个数字存到a[]中
for(int i=s.length()-1;i>=0;i--)
a[i]=(s.charAt(i)-'0');
for(int i=0;i<s.length();i++) { //从最高位处理到最低位
if(a[i]-B < 0)
if((a[i]+1<(9-a[i])|| A<9-a[i]) || A<B){
B -= a[i]+1;
a[i] = 9;
}
while(a[i]<9 && A!=0) {
a[i]++;
A--;
}
System.out.print(a[i]); //打印这一位的最大结果
}
}
}
Python代码。用DFS实现,和C++代码一样。
N,A,B=map(int,input().split())
s=list(map(int,str(N)))
def dfs(i,v):
global A,B,ans
if i==len(s):
ans=max(ans,v)
return
d=s[i]
t=min(A,9-d)
A -= t
dfs(i+1,10*v+d+t)
A+=t
if B > d:
B -= d+1
dfs(i+1,10*v+9)
B += d+1
ans=0
dfs(0,0)
print(ans)
买瓜
链接 买瓜
首先注意到评测用例中的n都不大,估计可以用暴力的搜索解决。
第i个瓜有三个选项:完整的瓜重Ai、半个瓜重Ai/2、不要这个瓜。本题简单的做法是对所有的瓜进行组合,每个瓜尝试三个选项。共有 3 n 3^n 3n种组合,可以通过约50%的测试。用DFS编码求组合。
C++代码。用到一个小技巧,为了避免除2出现小数,改为把m乘2,那么每个瓜的3个选项是:2Ai、Ai、0。
c++代码
#include 本题100%得分的代码需要用到分治法和二分,请自行搜索题解。
java代码
import java.util.Scanner;
public class Main {
static int n, m;
static int[] a;
static int ans = 40;
public static void dfs(int step, int s, int k) {
if (s > m || k >= ans) return;
if (s == m) {
ans = Math.min(ans, k);
return;
}
if (step == n + 1) return;
dfs(step + 1, s, k);
dfs(step + 1, s + a[step], k + 1);
dfs(step + 1, s + a[step] * 2, k);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt() << 1;
a = new int[n + 1];
for (int i = 1; i <= n; i++) a[i] = scanner.nextInt();
dfs(1, 0, 0);
System.out.println(ans == 40 ? -1 : ans);
}
}
python代码
def dfs(step, s, k):
global ans
if s > m or k >= ans: return
if s == m:
ans = min(ans, k)
return
if step == n + 1: return
dfs(step + 1, s, k)
dfs(step + 1, s + a[step], k + 1)
dfs(step + 1, s + a[step] * 2, k)
ans = 40
n, m = map(int, input().split())
m <<= 1
a = [0] * (n + 1)
a[1:] = map(int, input().split())
dfs(1, 0, 0)
print(-1 if ans == 40 else ans)
7. 习题
蓝桥杯题库的DFS题目:
https://www.lanqiao.cn/problems/?first_category_id=1&tags=DFS&sort=difficulty&asc=1