【机器学习】聚类算法(三)
六、基于图的算法
6.1 谱聚类
6.2 算法原理
RatioCut算法
NCut算法
6.3 如何选择合适的K值
6.4 谱聚类的应用场景
示例代码1:对鸢尾花数据集进行聚类,并绘制结果
# 导入所需的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics.pairwise import rbf_kernel
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
# 定义谱聚类的函数
def spectral_clustering(X, k, gamma):
# 计算相似度矩阵
S = rbf_kernel(X, gamma=gamma)
# 计算度矩阵
D = np.diag(np.sum(S, axis=1))
# 计算拉普拉斯矩阵
L = D - S
# 计算特征值和特征向量
eig_val, eig_vec = np.linalg.eig(L)
# 选择最小的k个特征值对应的特征向量
idx = np.argsort(eig_val)[:k]
U = eig_vec[:, idx]
# 对每一行进行归一化
T = np.linalg.norm(U, axis=1, keepdims=True)
U = U / T
# 应用k-means算法
kmeans = KMeans(n_clusters=k, random_state=0)
kmeans.fit(U)
# 返回簇标签
return kmeans.labels_
# 调用谱聚类的函数,设置k=3,gamma=0.1
y_pred = spectral_clustering(X, k=3, gamma=0.1)
# 绘制原始数据和聚类结果的散点图
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='rainbow')
plt.title('Original Data')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.subplot(122)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='rainbow')
plt.title('Spectral Clustering')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.show()示例代码2:
这是一个用于评估聚类结果的函数,它可以计算互信息、准确度和纯度等指标。这些指标都是用来评估聚类结果的有效性的。
互信息 (Mutual Information) 是衡量两个随机变量之间的依赖程度的一个度量,它反映了两个变量共享的信息量。在聚类中,互信息可以用来衡量聚类结果与真实标签之间的一致性,互信息越大,表示聚类结果越符合真实标签。
准确度 (Accuracy) 是衡量聚类结果与真实标签之间的匹配程度的一个度量,它反映了聚类结果中正确分类的样本比例。在聚类中,准确度可以用来衡量聚类结果的正确性,准确度越高,表示聚类结果越正确。
纯度 (Purity) 是衡量聚类结果中每个簇的纯净程度的一个度量,它反映了每个簇中占比最大的真实标签的比例。在聚类中,纯度可以用来衡量聚类结果的纯净性,纯度越高,表示聚类结果越纯净。
# 导入 math 模块,用于进行数学运算
import math
# 导入 numpy 模块,用于进行数组操作
import numpy as np
# 定义一个函数,名为 eva,接受两个参数,分别是 A 和 B,表示两种聚类结果的标签
def eva(A, B):
# 计算样本点数,即 A 和 B 的长度,赋值给 total
total = len(A)
# 将 A 中的不同标签转换为一个集合,赋值给 A_ids
A_ids = set(A)
# 将 B 中的不同标签转换为一个集合,赋值给 B_ids
B_ids = set(B)
# 初始化互信息为 0,赋值给 MI
MI = 0
# 定义一个很小的正数,赋值给 eps,用于避免对 0 取对数的错误
eps = 1.4e-45
# 初始化准确度为 0,赋值给 acc
acc = 0
# 初始化纯度为 0,赋值给 purity
purity = 0
# 对于 A 中的每个标签,赋值给 idA
for idA in A_ids:
# 初始化最大纯度为 0.0,赋值给 max_purity
max_purity = 0.0
# 对于 B 中的每个标签,赋值给 idB
for idB in B_ids:
# 找出 A 中标签为 idA 的样本的索引,赋值给 idAOccur
idAOccur = np.where(A == idA) # 返回下标
# 找出 B 中标签为 idB 的样本的索引,赋值给 idBOccur
idBOccur = np.where(B == idB)
# 找出 A 和 B 中同时标签为 idA 和 idB 的样本的索引,赋值给 idABOccur
idABOccur = np.intersect1d(idAOccur, idBOccur)
# 计算 A 中标签为 idA 的样本的比例,赋值给 px
px = 1.0*len(idAOccur[0])/total
# 计算 B 中标签为 idB 的样本的比例,赋值给 py
py = 1.0*len(idBOccur[0])/total
# 计算 A 和 B 中同时标签为 idA 和 idB 的样本的比例,赋值给 pxy
pxy = 1.0*len(idABOccur)/total
# 根据公式计算互信息,累加到 MI 上
MI = MI + pxy*math.log(pxy/(px*py)+eps, 2) # 互信息计算
# 如果 idA 和 idB 相等,说明 A 和 B 中的标签一致
if idA == idB:
# 将 pxy 累加到 acc 上,表示准确度
acc = acc + pxy # 准确度计算
# 如果 idABOccur 的长度大于 max_purity,说明这是一个较纯的簇
if len(idABOccur) > max_purity: # 纯度计算
# 更新 max_purity 的值
max_purity = len(idABOccur)
# 将 idABOccur 的比例累加到 purity 上,表示纯度
purity = purity + 1.0*len(idABOccur)/total
# 计算标准化互信息,即互信息除以 A 和 B 的熵的平均值
# 初始化 A 的熵为 0,赋值给 Hx
Hx = 0
# 对于 A 中的每个标签,赋值给 idA
for idA in A_ids:
# 计算 A 中标签为 idA 的样本的个数,赋值给 idAOccurCount
idAOccurCount = 1.0*len(np.where(A == idA)[0])
# 根据公式计算 A 的熵,累加到 Hx 上
Hx = Hx - (idAOccurCount/total)*math.log(idAOccurCount/total+eps, 2)
# 初始化 B 的熵为 0,赋值给 Hy
Hy = 0
# 对于 B 中的每个标签,赋值给 idB
for idB in B_ids:
# 计算 B 中标签为 idB 的样本的个数,赋值给 idBOccurCount
idBOccurCount = 1.0*len(np.where(B == idB)[0])
# 根据公式计算 B 的熵,累加到 Hy 上
Hy = Hy - (idBOccurCount/total)*math.log(idBOccurCount/total+eps, 2)
# 计算标准化互信息,赋值给 NMI
NMI = 2.0*MI/(Hx+Hy)
# 返回 NMI,acc 和 purity 三个指标
return NMI, acc, purity这是一个用于实现谱聚类算法的源代码,它可以对不同形状的数据进行聚类分析
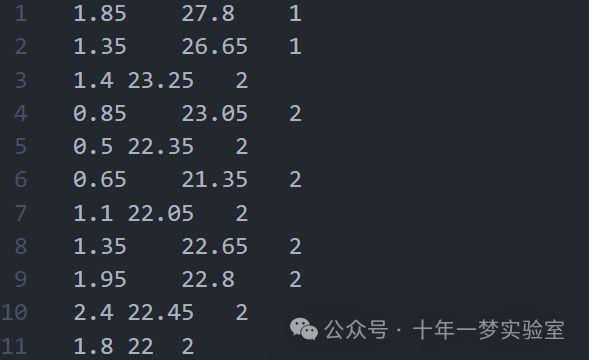
flame.txt 数据集
# 从 sklearn.cluster 模块导入 KMeans 函数,用于进行 K-Means 聚类
from sklearn.cluster import KMeans
# 导入 numpy 模块,用于进行数组操作
import numpy as np
# 导入 math 模块,用于进行数学运算
import math as m
# 导入 matplotlib.pyplot 模块,用于绘制图形
import matplotlib.pyplot as plt
# 导入 evaluate 模块,用于评估聚类结果
import evaluate as eval
# 定义几个数据集的文件名,用于读取数据
# flame.txt
# Jain_cluster=2.txt
# Aggregation_cluster=7.txt
# Spiral_cluster=3.txt
# Pathbased_cluster=3.txt
# 定义数据集的路径,这里使用 flame.txt 数据集
data_path = "Cluster-master\\data\\flame.txt"
def load_data():
"""
导入数据
:return:
"""
# 使用 numpy 的 loadtxt 函数读取数据文件,以制表符为分隔符,返回一个二维数组,赋值给 points
points = np.loadtxt(data_path, delimiter='\t')
# 返回 points
return points
def get_dis_matrix(data):
"""
获得邻接矩阵
:param data: 样本集合
:return: 邻接矩阵
"""
# 计算样本点的个数,赋值给 nPoint
nPoint = len(data)
# 创建一个 nPoint x nPoint 的零矩阵,赋值给 dis_matrix
dis_matrix = np.zeros((nPoint, nPoint))
# 对于每个样本点,赋值给 i
for i in range(nPoint):
# 对于 i 之后的每个样本点,赋值给 j
for j in range(i + 1, nPoint):
# 计算 i 和 j 两点之间的欧氏距离,赋值给 dis_matrix 的 i 行 j 列和 j 行 i 列
dis_matrix[i][j] = dis_matrix[j][i] = m.sqrt(np.power(data[i] - data[j], 2).sum())
# 返回 dis_matrix
return dis_matrix
def getW(data, k):
"""
利用KNN获得相似矩阵
:param data: 样本集合
:param k: KNN参数
:return:
"""
# 调用 get_dis_matrix 函数,获得邻接矩阵,赋值给 dis_matrix
dis_matrix = get_dis_matrix(data)
# 创建一个 nPoint x nPoint 的零矩阵,赋值给 W
W = np.zeros((len(data), len(data)))
# 对于每一行的距离,赋值给 each,同时记录其索引,赋值给 idx
for idx, each in enumerate(dis_matrix):
# 对每一行的距离进行排序,返回排序后的索引,赋值给 index_array
index_array = np.argsort(each)
# 将 W 的 idx 行的 index_array 中的第 1 到第 k+1 个元素设为 1,表示与 idx 最近的 k 个点
W[idx][index_array[1:k+1]] = 1
# 将 W 转置,赋值给 tmp_W
tmp_W = np.transpose(W)
# 将 W 和 tmp_W 相加,除以 2,得到对称的相似矩阵,赋值给 W
W = (tmp_W+W)/2
# 返回 W
return W
def getD(W):
"""
获得度矩阵
:param W: 相似度矩阵
:return: 度矩阵
"""
# 对 W 的每一行求和,得到一个一维数组,然后将其作为对角线元素,创建一个对角矩阵,赋值给 D
D = np.diag(sum(W))
# 返回 D
return D
def getL(D, W):
"""
获得拉普拉斯举着
:param W: 相似度矩阵
:param D: 度矩阵
:return: 拉普拉斯矩阵
"""
# 用 D 减去 W,得到拉普拉斯矩阵,赋值给 L
return D - W
def getEigen(L):
"""
从拉普拉斯矩阵获得特征矩阵
:param L: 拉普拉斯矩阵
:return:
"""
# 使用 numpy 的 linalg.eig 函数求解 L 的特征值和特征向量,分别赋值给 eigval 和 eigvec
eigval, eigvec = np.linalg.eig(L)
# 对特征值进行排序,返回最小的 cluster_num 个特征值的索引,赋值给 ix
ix = np.argsort(eigval)[0:cluster_num]
# 返回特征向量矩阵的 ix 列,即最小的 cluster_num 个特征向量,赋值给 eigvec
return eigvec[:, ix]
def plotRes(data, clusterResult, clusterNum):
"""
结果可视化
:param data: 样本集
:param clusterResult: 聚类结果
:param clusterNum: 聚类个数
:return:
"""
# 计算样本点的个数,赋值给 nPoints
nPoints = len(data)
# 定义一个颜色列表,用于绘制不同簇的样本点
scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange']
# 对于每个簇,赋值给 i
for i in range(clusterNum):
# 从颜色列表中选择一个颜色,赋值给 color
color = scatterColors[i % len(scatterColors)]
# 初始化两个空列表,用于存储该簇的样本点的横纵坐标,分别赋值给 x1 和 y1
x1 = []; y1 = []
# 对于每个样本点,赋值给 j
for j in range(nPoints):
# 如果样本点 j 的聚类结果等于 i,说明它属于该簇
if clusterResult[j] == i:
# 将样本点 j 的第一个特征值添加到 x1 中
x1.append(data[j, 0])
# 将样本点 j 的第二个特征值添加到 y1 中
y1.append(data[j, 1])
# 使用 matplotlib.pyplot 的 scatter 函数绘制该簇的散点图,横轴为 x1,纵轴为 y1,颜色为 color,透明度为 1,标记为 +
plt.scatter(x1, y1, c=color, alpha=1, marker='+')
# 显示图形
plt.show()
# 如果当前文件是主程序,执行以下代码
if __name__ == '__main__':
# 定义聚类的个数,赋值给 cluster_num
cluster_num = 2
# 定义 KNN 的参数,赋值给 KNN_k
KNN_k = 5
# 调用 load_data 函数,导入数据,赋值给 data
data = load_data()
# 将 data 转换为 numpy 数组,赋值给 data
data = np.asarray(data)
# 调用 getW 函数,获得相似矩阵,赋值给 W
W = getW(data, KNN_k)
# 调用 getD 函数,获得度矩阵,赋值给 D
D = getD(W)
# 调用 getL 函数,获得拉普拉斯矩阵,赋值给 L
L = getL(D, W)
# 调用 getEigen 函数,获得特征矩阵,赋值给 eigvec
eigvec = getEigen(L)
# 创建一个 K-Means 聚类器对象,设置簇的个数为 cluster_num,赋值给 clf
clf = KMeans(n_clusters=cluster_num)
# 对特征矩阵进行拟合,得到 K-Means 聚类的结果,赋值给 s
s = clf.fit(eigvec)
# 获取聚类的标签,赋值给 C
C = s.labels_
# 调用 eval.eva 函数,评估聚类结果的互信息、准确度和纯度,赋值给 nmi, acc, purity
nmi, acc, purity = eval.eva(C+1, data[:, 2])
# 打印 nmi, acc, purity 的值
print(nmi, acc, purity)
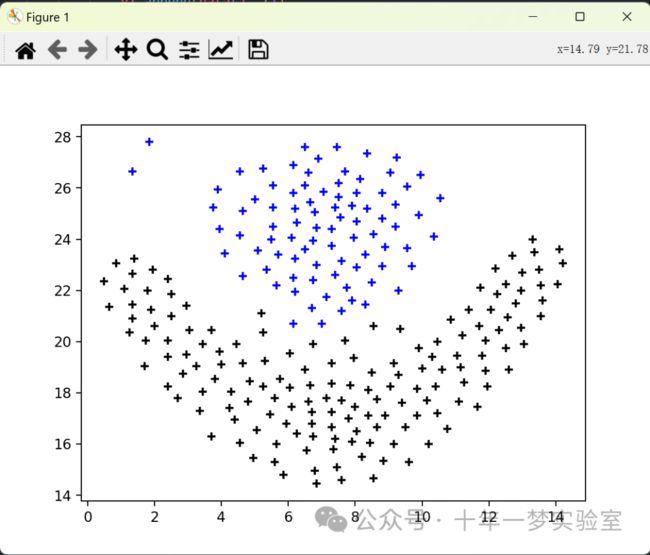
# 调用 plotRes 函数,绘制聚类结果的图形,传入样本数据、聚类标签和簇的个数
plotRes(data, np.asarray(C), 7)运行输出1:0.9354643343418292 0.008333333333333333 1.0
运行输出2:0.9354643343418292 0.9916666666666667 1.0
示例3-图像分割的光谱聚类
在这个示例中,我们生成了一个包含连接圆的图像,并使用谱聚类来分离这些圆。
在这些设置中,:ref:spectral_clustering 方法解决了被称为“归一化图割”的问题:图像被视为连接体素的图,而谱聚类算法相当于选择定义区域的图割,同时最小化沿切割的梯度与区域体积之比。
由于算法试图平衡体积(即平衡区域大小),如果我们取不同大小的圆,分割将失败。
此外,由于图像的强度或梯度中没有有用的信息,我们选择在仅由梯度微弱地指导的图上执行谱聚类。这类似于对图进行Voronoi分割。
此外,我们使用对象的掩模将图限制为对象的轮廓。在这个示例中,我们对将对象彼此分离感兴趣,而不是与背景分离。
# 导入 numpy 模块,用于进行数组操作
import numpy as np
# 定义一个常数,赋值给 l,表示图像的大小
l = 100
# 使用 numpy 的 indices 函数,生成一个 l x l 的网格,返回两个二维数组,分别表示网格的横纵坐标,赋值给 x 和 y
x, y = np.indices((l, l))
# 定义四个圆的圆心坐标,赋值给 center1, center2, center3, center4
center1 = (28, 24)
center2 = (40, 50)
center3 = (67, 58)
center4 = (24, 70)
# 定义四个圆的半径,赋值给 radius1, radius2, radius3, radius4
radius1, radius2, radius3, radius4 = 16, 14, 15, 14
# 计算网格中的每个点到圆心的距离,判断是否小于半径,得到一个布尔值的二维数组,表示每个点是否在圆内,赋值给 circle1, circle2, circle3, circle4
circle1 = (x - center1[0]) ** 2 + (y - center1[1]) ** 2 < radius1**2
circle2 = (x - center2[0]) ** 2 + (y - center2[1]) ** 2 < radius2**2
circle3 = (x - center3[0]) ** 2 + (y - center3[1]) ** 2 < radius3**2
circle4 = (x - center4[0]) ** 2 + (y - center4[1]) ** 2 < radius4**2
# %%
# 绘制四个圆
# ---------------------
# 将四个圆的布尔值数组相加,得到一个整数的二维数组,表示每个点属于几个圆,赋值给 img
img = circle1 + circle2 + circle3 + circle4
# 我们使用一个掩码,限制在前景区域:我们感兴趣的问题不是将对象与背景分离,而是将它们彼此分离。
# 将 img 转换为布尔值类型,赋值给 mask,表示前景区域
mask = img.astype(bool)
# 将 img 转换为浮点数类型,赋值给 img
img = img.astype(float)
# 在 img 上加上一些随机噪声,增加数据的复杂度
img += 1 + 0.2 * np.random.randn(*img.shape)
# %%
# 将图像转换为一个图,边的权重为梯度的值
# 从 sklearn.feature_extraction 模块导入 image 函数,用于将图像转换为图
from sklearn.feature_extraction import image
# 调用 image.img_to_graph 函数,传入 img 和 mask,得到一个稀疏矩阵,表示图的邻接矩阵,赋值给 graph
# graph = image.img_to_graph(img, mask=mask) 这行代码的作用是将图像 img 转换为图形表示,其中 mask 是一个布尔数组,用于指定哪些像素应该包含在图形中。
# image.img_to_graph 是 sklearn.feature_extraction 模块中的一个函数,它可以将一个二维或三维的图像数组转换为一个稀疏矩阵,表示图像中每个像素点与其相邻像素点的连接关系,也就是图中的节点和边。1
# img 是一个二维或三维的图像数组,表示原始的图像数据。在这个例子中,img 是一个二维的灰度图像,每个元素表示一个像素点的灰度值。
# mask 是一个与 img 形状相同的布尔数组,表示图像中的前景区域。在这个例子中,mask 是由四个圆形区域组成的,每个元素表示一个像素点是否属于前景区域。
# graph 是一个稀疏矩阵,表示图像中每个像素点与其相邻像素点的连接关系,也就是图中的节点和边。graph 的 shape 属性是 (n_pixels, n_pixels),其中 n_pixels 是图像中的像素点的总数。graph 的 data 属性是一个一维数组,表示图中边的权重,也就是图像中每个像素点的梯度值,即像素点的灰度值的变化程度。
graph = image.img_to_graph(img, mask=mask) # 将图像转换为边缘具有梯度值的图形
# %%
# 取梯度的一个递减函数,得到一个接近 Voronoi 划分的分割
# 将 graph 的 data 属性,即邻接矩阵的非零元素,用指数函数进行变换,使其变小,赋值给 graph.data
# graph.data = np.exp(-graph.data / graph.data.std()) 这行代码的作用是对图的邻接矩阵的非零元素进行变换,使其变小,从而降低边的权重,增加聚类的效果。
# np.exp 是 numpy 模块中的一个函数,它可以对一个数组或一个数进行指数运算,即 e 的 x 次方,其中 x 是数组或数的值。
# graph.data 是 graph 对象的一个属性,它是一个一维数组,表示图的邻接矩阵的非零元素,也就是图中边的权重。在这个例子中,边的权重是图像中每个像素点的梯度值,也就是像素点的灰度值的变化程度。
# graph.data / graph.data.std() 是对 graph.data 进行除法运算,除以 graph.data 的标准差,也就是 graph.data 的值的离散程度。这样可以使 graph.data 的值变得更加平滑,减少噪声的影响。
# np.exp(-graph.data / graph.data.std()) 是对 graph.data / graph.data.std() 的结果进行指数运算,然后取负号,这样可以使 graph.data 的值变得更加小,接近于 0。这样可以使边的权重变得更加小,从而增加聚类的效果,使得聚类结果更接近于 Voronoi 划分,也就是每个区域的中心点到其他区域的边界的距离最大。
graph.data = np.exp(-graph.data / graph.data.std())
# %%
# 在这里我们使用 arpack 求解器进行谱聚类,因为 amg 在这个例子上数值不稳定。然后我们绘制结果。
# 导入 matplotlib.pyplot 模块,用于绘制图形
import matplotlib.pyplot as plt
# 从 sklearn.cluster 模块导入 spectral_clustering 函数,用于进行谱聚类
from sklearn.cluster import spectral_clustering
# 调用 spectral_clustering 函数,传入 graph, n_clusters=4, eigen_solver="arpack",得到一个一维数组,表示每个点的聚类标签,赋值给 labels
labels = spectral_clustering(graph, n_clusters=4, eigen_solver="arpack")
# 创建一个与 mask 形状相同的全 -1.0 的数组,赋值给 label_im
label_im = np.full(mask.shape, -1.0)
# 将 label_im 中 mask 为 True 的位置,用 labels 的值替换,表示前景区域的聚类结果
label_im[mask] = labels
# 创建一个 1 行 2 列的子图,大小为 10 x 5,赋值给 fig 和 axs
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
# 在 axs 的第一个子图上,使用 matshow 函数绘制原始图像
axs[0].matshow(img) # 输入是二维的,表示灰度图像,那么 imshow 函数会根据 cmap 参数来选择颜色映射,将像素值转换为不同的颜色
# 在 axs 的第二个子图上,使用 matshow 函数绘制聚类结果
axs[1].matshow(label_im)
# 显示图形
plt.show()
# %%
# 绘制两个圆
# --------------------
# 在这里我们重复上面的过程,但只考虑我们生成的前两个圆。注意这样会得到一个更清晰的分割,因为区域的大小更容易平衡。
# 将 circle1 和 circle2 的布尔值数组相加,得到一个整数的二维数组,表示每个点属于几个圆,赋值给 img
img = circle1 + circle2
# 将 img 转换为布尔值类型,赋值给 mask,表示前景区域
mask = img.astype(bool)
# 将 img 转换为浮点数类型,赋值给 img
img = img.astype(float)
# 在 img 上加上一些随机噪声,增加数据的复杂度
img += 1 + 0.2 * np.random.randn(*img.shape)
# 调用 image.img_to_graph 函数,传入 img 和 mask,得到一个稀疏矩阵,表示图的邻接矩阵,赋值给 graph
graph = image.img_to_graph(img, mask=mask)
# 将 graph 的 data 属性,即邻接矩阵的非零元素,用指数函数进行变换,使其变小,赋值给 graph.data
graph.data = np.exp(-graph.data / graph.data.std())
# 调用 spectral_clustering 函数,传入 graph, n_clusters=2, eigen_solver="arpack",得到一个一维数组,表示每个点的聚类标签,赋值给 labels
labels = spectral_clustering(graph, n_clusters=2, eigen_solver="arpack")
# 创建一个与 mask 形状相同的全 -1.0 的数组,赋值给 label_im
label_im = np.full(mask.shape, -1.0)
# 将 label_im 中 mask 为 True 的位置,用 labels 的值替换,表示前景区域的聚类结果
label_im[mask] = labels
# 创建一个 1 行 2 列的子图,大小为 10 x 5,赋值给 fig 和 axs
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
# 在 axs 的第一个子图上,使用 matshow 函数绘制原始图像
axs[0].matshow(img)
# 在 axs 的第二个子图上,使用 matshow 函数绘制聚类结果
axs[1].matshow(label_im)
# 显示图形
plt.show()输出结果:
示例代码4:将希腊硬币图片分割成区域
此示例使用从图像的体素到体素差异创建的图上的 :ref:spectral_clustering,将该图像分解为多个部分同质的区域。
这个过程(在图像上的谱聚类)是寻找归一化图割的高效近似解决方案。
有三个选项可以分配标签:
'kmeans' 谱聚类在嵌入空间中使用 kmeans 算法对样本进行聚类
'discrete' 迭代搜索最接近谱聚类嵌入空间的分区空间
'cluster_qr' 使用带有枢轴的 QR 分解直接确定嵌入空间中的分区来分配标签。
# 导入 time 模块,用于计算运行时间
import time
# 导入 matplotlib.pyplot 模块,用于绘制图形
import matplotlib.pyplot as plt
# 导入 numpy 模块,用于进行数组操作
import numpy as np
# 从 scipy.ndimage 模块导入 gaussian_filter 函数,用于对图像进行高斯滤波
from scipy.ndimage import gaussian_filter
# 从 skimage.data 模块导入 coins 函数,用于加载硬币图像
from skimage.data import coins
# 从 skimage.transform 模块导入 rescale 函数,用于对图像进行缩放
from skimage.transform import rescale
# 从 sklearn.cluster 模块导入 spectral_clustering 函数,用于进行谱聚类
from sklearn.cluster import spectral_clustering
# 从 sklearn.feature_extraction 模块导入 image 函数,用于将图像转换为图
from sklearn.feature_extraction import image
# 调用 coins 函数,加载硬币图像,得到一个二维数组,赋值给 orig_coins
orig_coins = coins()
# 将图像缩放到原来的 20% 大小,以加快处理速度
# 在缩放之前,对图像进行高斯滤波,可以减少锯齿效应
# 调用 gaussian_filter 函数,对 orig_coins 进行高斯滤波,sigma 参数为 2,赋值给 smoothened_coins
smoothened_coins = gaussian_filter(orig_coins, sigma=2)
# 调用 rescale 函数,对 smoothened_coins 进行缩放,scale 参数为 0.2,mode 参数为 "reflect",anti_aliasing 参数为 False,赋值给 rescaled_coins
rescaled_coins = rescale(smoothened_coins, 0.2, mode="reflect", anti_aliasing=False)
# 调用 image.img_to_graph 函数,将 rescaled_coins 转换为一个图,边的权重为梯度的值,赋值给 graph
graph = image.img_to_graph(rescaled_coins)
# 取梯度的一个递减函数:一个指数函数
# beta 越小,聚类结果越独立于原始图像。当 beta=1 时,聚类结果接近于 Voronoi 划分
# 定义一个常数,赋值给 beta,表示指数函数的参数
beta = 10
# 定义一个常数,赋值给 eps,表示一个很小的数,用于避免除零错误
eps = 1e-6
# 将 graph 的 data 属性,即邻接矩阵的非零元素,用指数函数进行变换,使其变小,赋值给 graph.data
graph.data = np.exp(-beta * graph.data / graph.data.std()) + eps
# 需要手动选择要显示的分割区域的个数
# 当前版本的 'spectral_clustering' 不支持自动确定好的聚类个数
# 定义一个常数,赋值给 n_regions,表示要显示的分割区域的个数
n_regions = 26
# %%
# 计算并可视化分割结果
# 计算一些额外的特征向量,可能会加速特征分解
# 聚类质量也可能会从请求额外的分割区域中受益
# 定义一个常数,赋值给 n_regions_plus,表示额外的分割区域的个数
n_regions_plus = 3
# 使用默认的特征分解求解器 'arpack' 进行谱聚类
# 可以使用任何已实现的求解器:eigen_solver='arpack', 'lobpcg', 或 'amg'
# 选择 eigen_solver='amg' 需要一个额外的包 'pyamg'
# 聚类质量和计算速度主要由求解器的选择和容差 'eigen_tol' 的值决定
# TODO: 改变 eigen_tol 对于 'lobpcg' 和 'amg' 似乎没有效果 #21243
# 对于 assign_labels 参数的两个可能的值,分别进行循环
for assign_labels in ("kmeans", "discretize"):
# 记录当前的时间,赋值给 t0
t0 = time.time()
# 调用 spectral_clustering 函数,传入 graph, n_clusters=(n_regions + n_regions_plus), eigen_tol=1e-7, assign_labels=assign_labels, random_state=42,得到一个一维数组,表示每个点的聚类标签,赋值给 labels
labels = spectral_clustering(
graph,
n_clusters=(n_regions + n_regions_plus),
eigen_tol=1e-7,
assign_labels=assign_labels,
random_state=42,
)
# 记录当前的时间,赋值给 t1
t1 = time.time()
# 将 labels 重新整形为与 rescaled_coins 相同的形状,赋值给 labels
labels = labels.reshape(rescaled_coins.shape)
# 创建一个大小为 5 x 5 的图形,赋值给 plt.figure
plt.figure(figsize=(5, 5))
# 使用 plt.imshow 函数,显示 rescaled_coins,颜色映射为 plt.cm.gray
plt.imshow(rescaled_coins, cmap=plt.cm.gray)
# 设置 x 轴和 y 轴的刻度为空
plt.xticks(())
plt.yticks(())
# 定义一个字符串,赋值给 title,表示聚类的方法和运行时间
title = "Spectral clustering: %s, %.2fs" % (assign_labels, (t1 - t0))
# 打印 title
print(title)
# 使用 plt.title 函数,设置图形的标题为 title
plt.title(title)
# 对于从 0 到 n_regions 的每个整数,赋值给 l,分别进行循环
for l in range(n_regions):
# 定义一个列表,赋值给 colors,表示不同区域的颜色,使用 plt.cm.nipy_spectral 函数生成颜色映射
colors = [plt.cm.nipy_spectral((l + 4) / float(n_regions + 4))]
# 使用 plt.contour 函数,绘制 labels 等于 l 的区域的轮廓,颜色为 colors
plt.contour(labels == l, colors=colors)
# 如果想要查看每个区域的显示效果,可以取消注释 plt.pause(0.5)
# 使用 plt.show 函数,显示图形
plt.show()输出结果:
七、算法评价指标
聚类算法是一种无监督学习方法,它可以将数据点划分为不同的簇,根据它们之间的相似度或距离。聚类算法的评价指标可以分为两类。
聚类性能评估
Rand 指数
# Rand 指数
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.rand_score(labels_true, labels_pred) # 0.66...
# ARI 兰德指数不能确保对随机标记获得接近 0.0 的值。调整后的兰德指数校正了机会,并将给出这样的基线。
metrics.adjusted_rand_score(labels_true, labels_pred)#0.24...
# 与所有聚类指标一样,人们可以在预测标签中排列 0 和 1,将 2 重命名为 3,并获得相同的分数
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.rand_score(labels_true, labels_pred)
0.66...
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...
# rand_score 和 adjusted_rand_score 都是对称的:交换参数不会改变分数。因此,它们可以用作共识度量:
>>> metrics.rand_score(labels_pred, labels_true)
0.66...
>>> metrics.adjusted_rand_score(labels_pred, labels_true)
0.24...
# 完美的标签得分 1.0:
>>> labels_pred = labels_true[:]
>>> metrics.rand_score(labels_true, labels_pred)
1.0
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
1.0
# 差的同意标签(例如独立标签)得分较低,对于调整后的兰德指数,得分将为负或接近于零。然而,对于未调整的兰德指数,得分虽然较低,但并不一定接近于零。:
>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1]
>>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6]
>>> metrics.rand_score(labels_true, labels_pred)
0.39...
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
-0.07...基于互信息的评分
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504...
# 可以在预测标签中置换 0 和 1,将 2 重命名为 3 并获得相同的分数:
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504...
# 所有, mutual_info_score 、 adjusted_mutual_info_score 和 normalized_mutual_info_score 都是对称的:交换参数不会改变分数。因此,它们可用作共识度量:
>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true)
0.22504...
# 完美的标签得分 1.0:
>>> labels_pred = labels_true[:]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
1.0
>>> metrics.normalized_mutual_info_score(labels_true, labels_pred)
1.0
# 对于 mutual_info_score 来说并非如此,因此更难判断
>>> metrics.mutual_info_score(labels_true, labels_pred)
0.69...
# 差(例如独立标签)具有非正分数
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
-0.10526...同质性、完整性和 V 度量
鉴于对样本的地面实况类别分配的了解,可以使用条件熵分析来定义一些直观的度量。
特别是,Rosenberg 和 Hirschberg (2007) 为任何集群分配定义了以下两个理想目标:
同质性:每个簇仅包含一个类的成员。
完整性:给定类别的所有成员都被分配到同一个簇。
我们可以将这些概念转化为得分 homogeneity_score 和 completeness_score 。两者都以 0.0 为下限,以 1.0 为上限(越高越好):
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.homogeneity_score(labels_true, labels_pred)
0.66...
>>> metrics.completeness_score(labels_true, labels_pred)
0.42...
# 它们的调和平均数称为 V 度量,由 v_measure_score 计算:
>>> metrics.v_measure_score(labels_true, labels_pred)
0.51...>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.54...
# 更多权重将归因于同质性,并使用大于 1 的值
>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48...V-measure 实际上等同于上面讨论的互信息 (NMI),聚合函数为算术平均值 [B2011]。
同质性、完整性和 V 度量可以使用 homogeneity_completeness_v_measure 一次计算,如下所示:
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(0.66..., 0.42..., 0.51...)以下聚类分配略好,因为它具有同质性,但并不完整:
>>> labels_pred = [0, 0, 0, 1, 2, 2]
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(1.0, 0.68..., 0.81...)Fowlkes-Mallows 得分
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140...
# 可以在预测标签中置换 0 和 1,将 2 重命名为 3 并获得相同的分数
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140...
# 差(例如独立标签)得分为零:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.0轮廓系数
# 一组样本的轮廓系数是每个样本的轮廓系数的平均值。
>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)
# 在正常使用中,轮廓系数应用于聚类分析的结果。
>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
0.55...Calinski-Harabasz 指数
如果不知道真实标签,则可以使用 Calinski-Harabasz 指数( sklearn.metrics.calinski_harabasz_score )——也称为方差比率准则——来评估模型,其中较高的 Calinski-Harabasz 分数与具有更好定义的簇的模型相关。
指数是所有簇的簇间离散度之和与簇内离散度之和的比率(其中离散度定义为距离平方和):
>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)在正常使用中,Calinski-Harabasz 指数应用于聚类分析的结果:
>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabasz_score(X, labels)
561.62...戴维斯-鲍尔丁指数
如果不知道真实标签,可以使用戴维斯-鲍丁指数 ( sklearn.metrics.davies_bouldin_score ) 来评估模型,其中较低的戴维斯-鲍丁指数与具有更好簇间分离的模型相关。
该指数表示簇之间的平均“相似性”,其中相似性是一种度量,用于比较簇之间的距离与簇本身的大小。
零是最低可能的分数。接近零的值表示更好的分区。
在正常使用中,Davies-Bouldin 指数应用于聚类分析的结果,如下所示
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
from sklearn.cluster import KMeans
from sklearn.metrics import davies_bouldin_score
kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans.labels_
davies_bouldin_score(X, labels)应急矩阵
偶然矩阵 ( sklearn.metrics.cluster.contingency_matrix ) 报告了每个真/预测簇对的交集基数。偶然矩阵为所有聚类指标提供了充分的统计数据,其中样本是独立且分布相同的,并且不需要考虑某些实例未被聚类的情况。
这是一个例子:
>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])输出数组的第一行表明有三个样本的真实簇为“a”。其中,两个在预测簇 0 中,一个在 1 中,没有一个在 2 中。第二行表明有三个样本的真实簇为“b”。其中,没有一个在预测簇 0 中,一个在 1 中,两个在 2 中。
分类的混淆矩阵是一个方块列联表,其中行和列的顺序对应于一个类列表
配对混淆矩阵
>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
[0, 4]])
>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
[0, 4]])将所有类成员分配给相同簇的标记是完整的,但可能并不总是纯净的,因此受到惩罚,并且有一些非对角线非零条目
>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
[0, 2]])矩阵不是对称的:
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
[2, 2]])如果类成员完全分散在不同的集群中,则分配完全不完整,因此矩阵的所有对角线条目均为零:
>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0, 0],
[12, 0]])参考网址:
https://scikit-learn.org/stable/auto_examples/cluster/plot_coin_segmentation.html#sphx-glr-auto-examples-cluster-plot-coin-segmentation-py