2023年12月23日~2024年1月5日周报（调试CNN-RWI代码、继续研读论文）

一、前言

        上周对CNN-RWI论文进行了初步研读，但是只是了解了大概，很多问题也只是停留在表面，没有进行深入思考。

        本周带着一系列问题继续研读CNN-RWI论文，并对代码进行初步学习。

        问题描述：

•  ①为什么阈值大小设置为网格点总数的1%；
•  ②根据特征分类，究竟是依据什么特征分类，分类后表明不同速度类型，还是其他方面；
•  ③地震观测记录、初始速度模型、RTM图像之间的关系；

二、学习情况

2.1 Git学习记录

        Git全称是分布式版本控制系统，git通常在编程中会用到，并且git支持分布式部署。分布式相比于集中式的最大区别在于开发者可以提交到本地，每个开发者通过克隆 (git clone)，在本地机器上拷贝一个完整的Git仓库。工作原理及流程如下：

        其中： 

• Workspace：工作区
• Index / Stage：暂存区
• Repository：仓库区（或本地仓库）
• Remote：远程仓库

2.1.1 Git的安装

        在Git官网下载对应系统的软件，下载地址为： git-scm.com或者gitforwindows.org，或者阿里镜像。

• git-scm 是 Git 的官方，里面有不同系统不同平台的安装包和源代码；
• gitforwindows.org 里只有 windows 系统的安装包。
• 阿里镜像Ctrl+F 搜索最新版本前缀即可，如2.40.0。

2.1.2 Git在Pycharm中的使用方法

        （1）确保计算机已经成功安装Git；

        （2）安装完成后，打开Pycharm，进入菜单栏中的“Setting”；

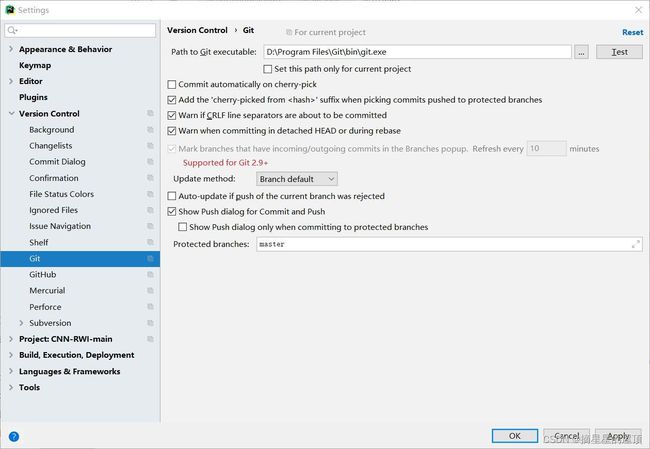
        （3）在“Setting”窗口中，找到“Version Control”选项，并点击进入；

        （4）在“Version Control”选项中，找到“Git”点击进入；

        （5）在“Git”选项中，找到“Path to Git executable”的字段，找到安装的Git的可执行文件的路径；

        （6）选择正确的路径后，点击“OK”或者“apply”来保存设置；

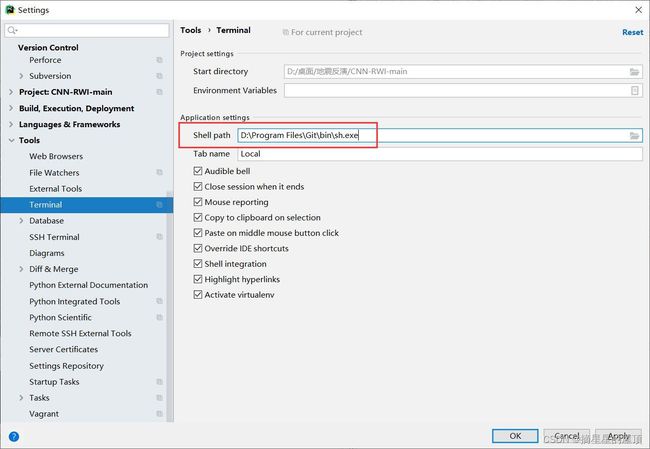
        （7）在Pycharm中设置Terminal： File—>Settings—>Tools—>Terminal—>Shell path

        （8）将cmd.exe改成刚刚下载的git的路径，注意选择的是sh.exe，不是git.exe

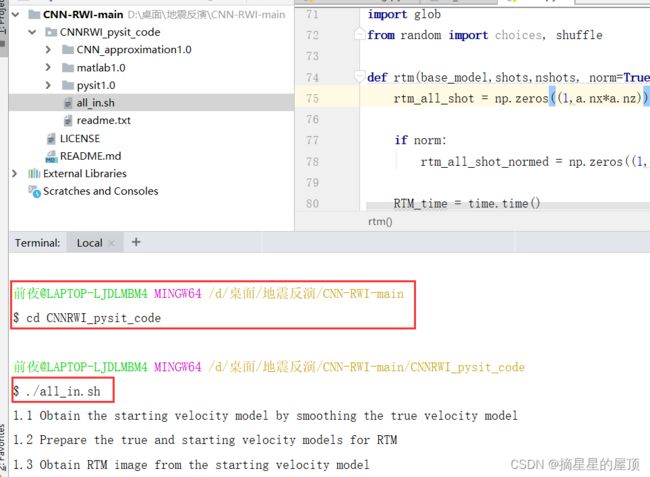
2.1.3 运行.sh文件

        在Terminal中运行：首先进入sh文件所在的目录，进入后即可开始运行

 

2.2 PySIT：Seismic Inversion Toolbox in Python 

         学习链接：PySIT Documentation — PySIT v1.0

         PySIT是Python的地震反演算法和波求解器的集合。这个软件包被设计为开发地震数据反演高级技术的测试台环境。

安装PySIT的依赖项：

• Python 3.7
• NumPy 1.7（或更高版本）
• SciPy 0.12（或更高版本）
• matplotlib 1.3（或更高版本）
• PyAMG 2.05（或更高版本）：是一个用于代数多重网格（AMG）方法的Python库。它提供了一个方便的Python界面，用于解决线性系统的快速和高效求解。

        PyAMG的安装可以通过pip、conda或源代码安装。

# pip安装
pip install pyamg
# conda安装
conda config --add channels conda-forge
conda install pyamg

        安装完成后，可以在Python代码中导入PyAMG并使用它来解决线性系统。下面代码演示了如何使用PyAMG来求解一个简单的线性系统（如何区分线性系统与非线性系统 - 知乎 (zhihu.com)）：

import numpy as np
import pyamg

# 创建一个稀疏矩阵
A = pyamg.gallery.poisson((100, 100))

# 创建一个随机向量
b = np.random.rand(A.shape[0])

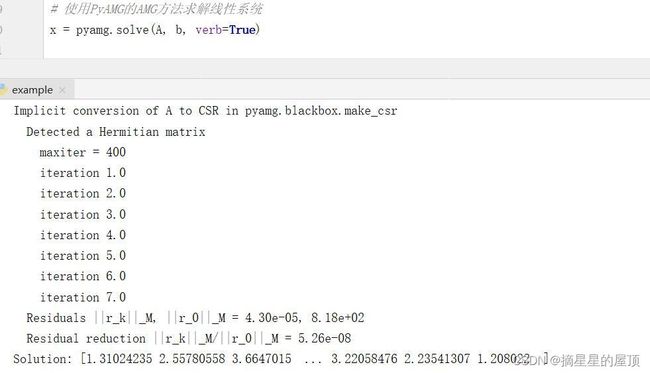
# 使用PyAMG的AMG方法求解线性系统
x = pyamg.solve(A, b, verb=True)

print("Solution:", x)

         上述代码中，首先创建了一个100x100的稀疏矩阵A和一个随机向量b。然后，我们使用PyAMG的solve函数来求解线性系统Ax=b，并将结果存储在变量x中。最后，打印出求解结果。

 

• ObsPy 0.85（或更高版本）：是一款针对地震领域开发的Python库，它提供了一组用于读取、处理、分析和可视化地震学数据的模块和函数。ObsPy支持多种地震学数据格式，包括SEED、SAC、MiniSEED等，并提供了丰富的功能，如申请数据时需要用 UTCDateTime 对象来控制发震时刻、申请波形数据的起始时间和结束时间等，可以读写地震数据、地震目录和元数据，进行波形绘制，从数据中心申请地震数据。ObsPy还提供了一些方便的工具，用于处理地震学数据的常见任务，滤波、插值、旋转等。通过使用ObsPy，地震学家可以更轻松地处理和分析地震学数据，并进行相关的科学研究。（安装方法：obspy安装 - CSDN文库）（学习参考：ObsPy Documentation (1.4.0) — ObsPy 1.4.0 documentation）

对于可选的并行支持，PySIT可以依赖于：

• MPI4Py 1.3.1（或更高版本）

        安装方式：

         （1）pip安装：

pip install pysit --pre
# 升级操作
pip install pysit --upgrade

        （2）git安装：

# 1.从github上托管的主存储库克隆PySIT
git clone https://github.com/pysit/pysit.git
# 2.进入PySIT克隆目录的根目录下，运行：
python setup.py install

        在PySIT的文档介绍中，有对Marmousi2数据的可视化展示教程，但是对计算机环境要求较高。 

 

2.3 shell脚本学习

        shell脚本是shell命令组成的可执行文件，将一些命令整合到一个文件中，进行处理业务逻辑，脚本不用编译即可运行。它通过解释器解释运行，速度相对来说比较慢。

        学习参考：一篇教会你写90%的shell脚本 - 知乎 (zhihu.com)

2.3.1 注释

        “ # ”开头的表示注释，被编译器忽略

• 单行注释： #
• 多行注释： :<

2.3.2 变量及操作

        运行shell时，存在三种变量：

1. 局部变量：在脚本或命令中定义，仅在当前shell实例中有效，其他shell启动的程序不能访问局部变量。
2. 环境变量：所有的程序（包括shell启动的程序）都能访问环境变量，有些程序需要环境变量来保证其正常运行。必要的时候shell脚本也可以定义环境变量。
3. shell变量：shell变量是由shell程序设置的特殊变量。shell变量中有一部分是环境变量，有一部分是局部变量，这些变量保证了shell的正常运行。

        变量操作：

• 创建普通变量：name="test" （=两边不可有空格）
• 创建只可函数体中使用的局部变量： local name="test" （使用local修饰的变量在函数体外无法访问，并且local只能在函数体内使用）
• 变量重新赋值： name="new_test" （将原值覆盖）
• 只读变量： name="only_read" -> readonly name （使用readonly标识后的变量，不可被修改）
• 删除变量： unset name; （删除之后不可访问，删除不掉只读变量）

        引用变量：

• 使用 $ 符号直接进行引用，包括循环变量

matlab_dir='matlab1.0/'
vel_dir='Marmousi/'
cd $matlab_dir$vel_dir

• 利用 双引号" " 将括起来的字符串支持变量插值

sh_num_smooth_iteration=400
"sh_num_smooth_iteration=$sh_num_smooth_iteration"
# sh_num_smooth_iteration=400

• 使用  ${ }  作为单词边界—推荐

iteration=0
matlab_filename=${iteration}"th_mig_"
# matlab_filename=0th_mig_

• 使用  ${#}  获取变量字符串长度

2.4 CNN-RWI代码学习

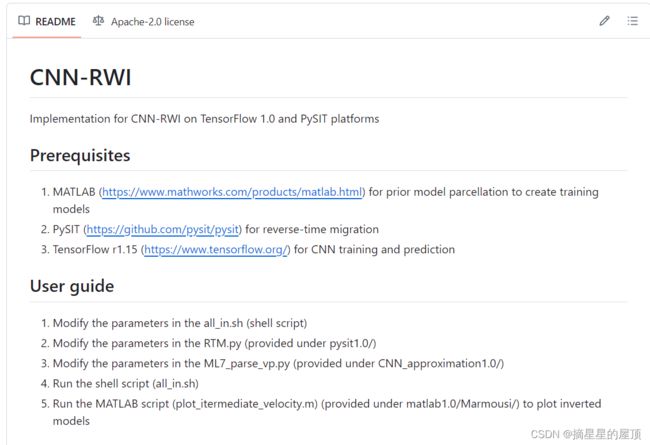
        下图是CNN-RWI代码的学习指南。  

        在代码中涉及很多之前没有接触到的知识，比如波形求解器、RTM偏移图像、shell脚本、TensorFlow等

        代码中采用argparse模块完成命令行选项与参数的设置 。

        TensorFlow是一个开源的机器学习框架，主要用于构建和训练深度学习模型，其主要作用包括：

1. 构建和训练深度学习模型：TensorFlow提供了一套高级的API和工具，让用户能够轻松地定义、训练和部署深度学习模型。它支持各种深度学习架构，如卷积神经网络（CNN）、循环神经网络（RNN）和生成对抗网络（GAN）等。
2. 分布式计算：TensorFlow支持分布式训练，能够在多台机器上运行计算，提高训练速度和模型的准确性。它还提供了各种优化算法，如梯度下降、Adam等，帮助用户更好地训练模型。
3. 跨平台应用：TensorFlow可以在各种硬件上运行，包括CPU、GPU和TPU等。它还提供了各种语言的接口，如Python、C++、Java等，让用户能够轻松地在不同的平台上部署模型。
4. 机器学习工作流：TensorFlow提供了一套完整的工作流，从数据预处理、模型定义、训练到部署，都能够在一套统一的框架下完成。这使得用户能够更加高效地开发和部署深度学习模型。
5. 社区支持：TensorFlow拥有庞大的社区，有大量的教程、案例和模型可供参考和使用。这使得用户在学习和使用TensorFlow时有丰富的资源可供参考。

2.4.1 tf.placeholder()函数

  tf.placeholder() 是 TensorFlow 1.x 版本中的一个函数，用于在计算图中创建一个占位符节点。占位符是在图执行期间预期会传递某种输入张量的特殊节点。这个函数常常早TensorFlow 代码的开始部分被用来设定占位符，然后这些占位符会被具体的值替换。

import tensorflow as tf  
  
# 创建一个占位符，用于接收输入数据  
input_data = tf.placeholder(tf.float32, shape=[None, input_size])

         在上面这个例子中，tf.placeholder() 创建了一个名为 input_data 的占位符节点，该节点预期在计算图执行期间接收一个形状为 [batch_size, input_size] 的二维张量。tf.float32 指定了该张量中的数据类型应为浮点数。

        需要注意的是，TensorFlow 2.x 已经弃用了静态计算图和 tf.placeholder()，取而代之的是更加灵活的 Eager Execution 模式和动态计算图。在 TensorFlow 2.x 中，推荐使用 tf.Tensor 和 tf.function 来定义和训练模型。

2.4.2 tf.train.Saver()函数

  tf.train.Saver() 是 TensorFlow 中用于保存和恢复模型的工具，这个类用于在训练过程中定期保存和加载训练过程中的模型权重和配置，以便在训练中断或其他情况下能够恢复训练，如硬件故障或长时间运行的任务被中断。以下是 tf.train.Saver() 的一些关键参数和功能：

1. var_list：一个变量列表，指定要保存的变量。如果未指定，则会保存所有可训练的变量。
2. max_to_keep：保存的模型检查点文件的最大数量。当保存的检查点数量超过这个值时，最早的模型会被自动删除。
3. keep_checkpoint_every_n_hours：每隔多少小时保存一个检查点，即使没有达到 max_to_keep 的限制。
4. defer_build：默认为 False。如果设置为 True，则在调用 build() 方法之前不会进行任何操作。这对于在使用 tf.train.MonitoredTrainingSession 时的早期检查点操作很有用。
5. restore_sequentially：默认为 False。如果设置为 True，则变量的恢复将按顺序进行，这有助于减少 GPU 内存的使用。
6. filename：检查点文件的名称模式。通常使用 "model" 或 "model-checkpoint_{epoch}" 等格式。

import tensorflow as tf  
  
# 定义模型和优化器  
model = ...  
optimizer = ...  
  
# 创建 Saver 对象  
saver = tf.train.Saver()  
  
# 在训练循环中定期保存模型  
with tf.Session() as sess:  
    for epoch in range(num_epochs):  
        # 训练模型...  
        sess.run(optimizer, feed_dict={...})  
          
        # 每隔一定数量的 epochs 保存模型  
        if epoch % save_interval == 0:  
            saver.save(sess, "model-checkpoint", global_step=epoch)

        在上面的示例中，首先定义了模型和优化器，然后创建了一个 tf.train.Saver() 对象。在训练循环中，定期调用 saver.save() 方法来保存模型的权重。这样，即使在训练过程中发生中断，也可以使用 tf.train.Saver().restore() 方法来恢复训练。 

2.5 论文题目选取

         在本周对毕业设计论文题目进行了思考，根据近段时间的学习情况，考虑以下选题：

• 《基于UNet的二维断层数据反演方法设计与实现》
• 《基于CNN的二维断层数据反演方法设计与实现》

        之前对CNN与Unet的的区别不太了解。比如CNN-RWI这篇文章，为什么取名为《自适应反馈机制下基于卷积神经网络的高清晰反射波反演算法（CNN-RWI）》，但是网络架构使用Unet呢？

• CNN（卷积神经网络）是一种图像级的分类器，主要用于识别图像中的类别，而Unet则是一种像素级的分类器，能够为图像中的每个像素点赋予相应的类别标签。
• CNN通过卷积层和池化层提取图像特征，然后经反向传播确定最终参数，并得到最终的特征；Unet的特征提取步骤较为复杂，包括Encoder和Decoder（编码器和解码器）两个部分。在Encoder部分，图像经过重复的下采样、卷积、下采样过程，提取图像的深度特征。在Decoder部分，通过上采样、深层特征与浅层特征的融合、卷积等步骤，逐渐恢复图像的细节信息，同时预测每个像素的类别。
• CNN更适合用于图像级别的分类任务，而Unet则更适合像素级别的分类任务，如语义分割等。

        对于闵老师博客中提到的第五部分的数据训练方式，比如迁移学习、多任务学习等，不太了解，所以没有进行选择。

三、遇到的部分问题及解决

3.1 上周遗留的问题

1.  为什么阈值大小设置为网格点总数的1%？

        文章中提及对于阈值的设置主要考虑了两个因素：

• 模型基础的质量：在每次迭代的时候准备具有24个样本的训练模型集合，应用空间约束、分割、分层k均值分组方法，以分别从第一次迭代的初始速度模型或从后续迭代的CNN预测速度模型构建模型基础。阈值设置为655，即模型网格点总数（256 × 256 = 65536）的1%。阈值设置为最大化模型基础中的组件数量（分层树中的叶节点的数量），并限制不创建无意义的小散射区域。
• 计算成本：阈值越小，分层树的深度就越大，会以指数方式增加将子模型进一步打包为更小特征作为模型基础的组件的计算时间。

     2. 根据特征分类，究竟是依据什么特征分类，分类后表明不同速度类型，还是其他方面？

        在基于K-means方法中，基于速度分布对模型进行划分。

     3. 地震观测记录、初始速度模型、RTM图像之间的关系？

        地震观测记录是对一次地震的从起始至终结全过程中的观测记载，包括震幅、频率、波形、时间等。这些数据通常以图表的形式进行汇总收集，并用于分析地震的基本参数，如发震时刻、震中经纬度、震源深度及震级等。通过地震观测记录，可以了解地震发生的过程和规律，为地震研究和预防提供基础资料。

        初始速度模型是指在地震勘探中，为了反演得到更准确的地质构造和地球物理参数，首先建立一个简单的地震波传播速度模型。这个模型是基于对区域地质的了解和一些假设，用于指导后续的反演计算。在建立初始速度模型时，需要考虑多种因素，如地层分布、岩石类型、构造特征等。这个模型可以是一个简单的层状模型，也可以是一个更复杂的模型，具体取决于研究区域的特点和需求。在反演过程中，初始速度模型会不断被修正和优化，以逐渐逼近真实的地质情况。这个过程通常需要多次迭代和调整，因此初始速度模型也被称为迭代初值模型。初始速度模型是地震勘探中不可或缺的一部分，它为后续的反演计算提供了初始条件和指导，是提高反演精度和准确性的重要保障。

        叠前逆时偏移（RTM）方法是目前地震勘探领域最为精确的一种地震数据成像方法，主要运用声波方程进行波场延拓，可以实现对复杂构造介质的准确成像，为地球物理学家提供了创建地下3D图像的能力。

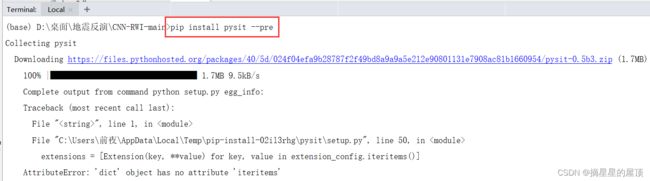
3.2 安装Pysit

        问题描述：'dict' object has no attribute 'iteritems'

        可能的原因：python版本问题

        解决方法：更换安装方式，先安装git得以解决。

3.3 公式 || || 的理解

        在数学中，双竖线“||”通常表示范数（norm）的概念。范数是衡量向量大小的一个量度，它可以用来度量向量在某个空间中的“长度”或者“大小”。具体的范数定义取决于所使用的空间和定义方式。

        例如，在欧几里得空间中，对于一个向量x = (x1, x2, ..., xn)，其L2范数定义为：

        ||x|| = √(x1^2 + x2^2 + ... + xn^2)

        这实际上就是向量x的长度。

        在其他类型的空间中，如L1范数、无穷范数等，范数的定义会有所不同。所以，双竖线“||”的具体意义需要结合上下文和所使用的数学空间来理解。

四、总结

4.1 存在的疑惑

1. 毕业设计题目知网中文论文较少，应该去哪里寻找呢？
2. 对于InversionNet网络结构的创新，应该从哪些方面考虑呢？比如：网络结构、网络的层度和深度这些吗

4.2 下周安排

        对InversionNet网络结构的进行创新。