《算法从入门到入土系列》第一集 搜索专题（DFS与BFS）题目解析 + 练习题单（更新ing）

菜鸡笔记，莫怪

蓝桥杯将近，DFS和BFS作为省赛常考的类型，这里整理一下常见的搜索的题型。(学习交流，比较菜，有什么不对的地方，请批评指正 ！！！)
稍后逐渐每一份代码会补上 Java代码（我报了Java组的蓝桥杯 希望这次别翻车）
（部分未完成，稍后补上）

搜索

BFS使用队列实现：先将初始状态加入到空的队列中，然后每次取出队首元素，找出队首所能转移到的状态，再将其压入队列中；如此反复，知道队列为空，这样就能保证一个状态再被访问的时候一定是采用的最短路径：

BFS的一般形式：

queue<type> q;
q.push(初始状态);//将初始状态入队
while (!q.empty()) {
    auto t = q.front();
    q.pop();
    for (枚举所有可扩展状态) //找到t的所有可达状态v
    	if (合法) //v需要满足某些条件，例如，未越界，未被访问过等等
    		//入队（同时可能需要维护某些信息，例如，维护当前状态是由哪个状态转移过来的，记录路径）
    		q.push(v);
}

BFS

AcWing 844. 走迷宫

链接：Click here~~

题解：搜索每一个点，以当前点向四周搜索，判断可搜索条件，记录当前点到起点的距离，第一次搜到终点的路径就是最短路径。

#include
#define x first
#define y second
using namespace std;
const int N = 110;
const int M = N * N;
typedef pair<int, int> PII;
int n, m;
int g[N][N];
int dist[N][N];//记录每个点到起点的距离
PII q[M];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int bfs() {
    int hh = 0, tt = 0;
    q[0] = {0, 0};//起点
    memset(dist, -1, sizeof dist);
    dist[0][0] = 0; 
    
    while (hh <= tt) {
        auto t = q[hh++];//取出队首元素
        //利用方向数组，枚举当前位置的4个方向
        for (int i = 0; i < 4; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            //判断条件要细心
            if (a < 0 || a >= n || b < 0 || b >= m) continue;
            if (g[a][b] == 1) continue;
            if (dist[a][b] != -1) continue;
            dist[a][b] = dist[t.x][t.y] + 1;//距离+1
            q[++tt] = {a, b};//将该位置放入队列
        }
    }
    return dist[n - 1][m - 1];//返回最后一个点
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    
    cout << bfs() << endl;
    return 0;
}

POJ 1426 “Find The Multiple”（待更新）

POJ 3126 “Prime Path”（待更新）

POJ 3414 Pots

HDU1240 Asteroids! （daige）

Flood Fill 算法

AcWing 1097. 池塘计数

链接：Click here~~

题意：有一篇N*M的矩形土地，其中 ‘W’ 表示水，’.’ 表示空地，一个水洼，一片连通的水，这个题是八连通，要求统计有多少片水洼。

（连通分两种，一种是四连通，一种是八连通）

解法：一个点一个点的扫描，当扫描到一片水也就是’W’时且这个’W’还没有被标记过，就以当前点为起点进行一次BFS(flood fill)，将与当前点连通的地图打标记，最后进行了几次BFS(flood fill)就是有几个连通块。也就是水洼的个数

BFS解法（数组模拟队列）：

//Flood Fill
//这里可以开标记数组 bool st[N][N];也可以把走过的 W 改成 . 即可
#include
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;//pair是因为每个点是一个坐标
const int N = 1010;
const int M = N * N;//M是存队列的，因为是一个点一个点的扫描所以总共有N * N个点
char g[N][N];
PII q[M];
int n, m;
bool st[N][N];//判重数组，一般情况下bfs都需要判重 state的一个缩写
void bfs(int xx, int yy) {
    int hh = 0, tt = 0;//初始化
    q[0] = {sx, sy};//起点
    //g[xx][yy] = '.';
    st[xx][yy] = true;//已经走过
    
    while (hh <= tt) {
        PII t = q[hh++];//拿出队头元素
        //遍历该点周围的8个点，八连通，写双重循环
        for (int i = t.x - 1; i <= t.x + 1; i++) {
            for (int j = t.y - 1; j <= t.y + 1; j++) {
                //九宫格中间挖空
                if (i == t.x && j == t.y) continue;
                //考虑边界
                if (i < 0 || i >= n || j < 0 || j >= m) continue;
                //如果当前点不是水，或者这个点已经走过了
    		   //g[i][j] == '.';
                if (g[i][j] == '.' || st[i][j]) continue;
                q[++tt] = {i, j};//满足题意，存入队列中
                //g[i][j] = '.';
                st[i][j] = true;//标记
            }
        }
    }
}
int main()
{

    scanf("%d%d", &n,&m);
    for (int i = 0; i < n ; i++) scanf("%s", &g[i]);
    
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            //是水，没被遍历过
            //第二种方法：
            //if (g[i][j] == 'W') {
            if (g[i][j] == 'W' && !st[i][j]) {
                bfs(i, j);
                cnt++;
            }
        }
    }
    
    printf("%d\n", cnt);
    return 0;
}

BFS解法（STL队列）：

#include
#define x first
#define y second
using namespace std;
const int N = 1010;
int n, m;
char g[N][N];//存图

// 方向数组
// int dx[9] = {0, -1, -1, 0, 1, 1, 1, 0, -1};
// int dy[9] = {0, 0, 1, 1, 1, 0, -1, -1, -1};

queue<pair<int, int>> q;

void bfs(int xx, int yy) {
    //将当前遍历到的点放进队列
    q.push({xx, yy});
    //已经遍历过了，改为.  ,也可以开一个st[N][N]，记录当前点已经搜过了
    g[xx][yy] = '.';
    
    while (q.size()) {
        auto t = q.front();
        
        // 方式1：方向数组
        // for (int i = 1; i <= 8; i++) {
        //     int a = t.x + dx[i], b = t.y + dy[i];
        //     if (a < 0 || a >= n || b < 0 || b >= m) continue;
        //     if (g[a][b] == '.') continue;
        //     q.push({a, b});
        //     g[a][b] = '.';
        // }
        
        // 方式2：八连通，枚举九宫格除了中间当前这个点
        for (int i = t.x - 1; i <= t.x + 1; i++) {
            for (int j = t.y - 1; j <= t.y + 1; j++) {
                if (i == t.x && j == t.y) continue;
                if (i < 0 || i >= n || j < 0 || j >= m) continue;
                if (g[i][j] == '.') continue;
                q.push({i, j});
                g[i][j] = '.';
            }
        }
        q.pop();
    }
    
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    cin >> n >> m;
    for (int i = 0; i < n; i++) cin >> g[i];
    
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            //遇到W就开始搜索周围
            if (g[i][j] == 'W') {
                bfs(i, j);
                cnt++;
            }
        }
    }
    
    cout << cnt << endl;
    return 0;
}

Java代码

import java.io.*;
import java.util.*;
class pair{
    int x, y;
    public pair(int x, int y){
        this.x = x;
        this.y = y;
    }
}
public class Main {
    static int N = 1010, n, m;
    static char[][] g;

    public static void bfs(int xx, int yy) {
        Queue<pair> q = new LinkedList<>();
        q.offer(new pair(xx, yy));
        while (!q.isEmpty()) {
            pair t = q.poll();
            for (int i = t.x - 1; i <= t.x + 1; i++) {
                for (int j = t.y - 1; j <= t.y + 1; j++) {
                    if (i == t.x && j == t.y) continue;
                    if (i < 0 || i >= n || j < 0 || j >= m) continue;
                    if (g[i][j] == '.') continue;
                    q.offer(new pair(i, j));
                    g[i][j] = '.';
                }
            }
        }
    }
    public static void main(String[] args) throws Exception {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        String[] cur = in.readLine().split(" ");
        n = Integer.parseInt(cur[0]);
        m = Integer.parseInt(cur[1]);
        g = new char[n][m];
        for (int i = 0; i < n; i++) {
            char[] arr = in.readLine().toCharArray();
            g[i] = arr;
        }

        int ans = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (g[i][j] == '.') continue;
                bfs(i, j);
                ans++;
            }
        }
        System.out.println(ans);
    }
}

DFS 解法：

#include

#define x first
#define y second

using namespace std;
const int N = 1010;
char g[N][N];
int n, m;
//定义8个方向
int dx[8] = {1, 0, -1, 0, 1, -1, 1, -1};
int dy[8] = {0, 1, 0, -1, 1, -1, -1, 1};
void dfs(int xx, int yy) {
    g[xx][yy] = '.';
    //遍历8个方向
    for (int i = 0; i < 8; i++) {
        int a = xx + dx[i], b = yy + dy[i];
        if (g[a][b] == 'W') dfs(a, b);
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (g[i][j] == 'W') {
                dfs(i, j);
                cnt++;
            }
        }
    }
    cout << cnt << endl;
    return 0;
}

AcWing 1098. 城堡问题

链接：Click here~~

题意：编写一个程序，计算城堡共有多少个房间 和 最大房间的面积（方块）

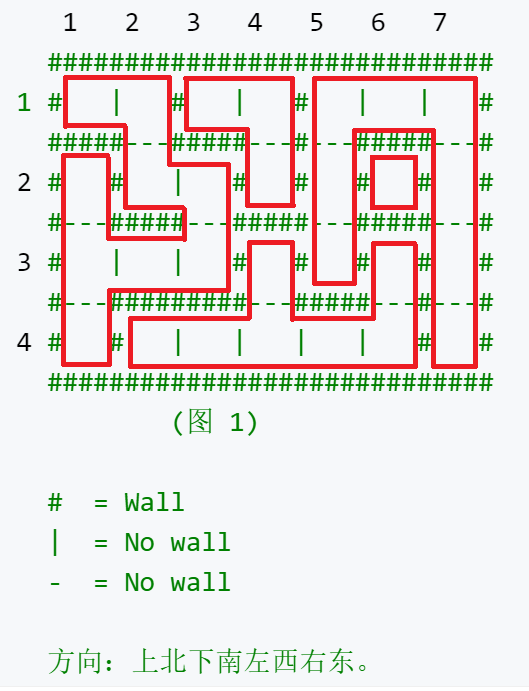
房间的个数如红色框框所示

题解：遍历每个点，用flood fill，

方向：左上右下，对应 1 2 4 8
int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};

g[t.x][t.y] >> i && 1的结果，刚好对应四个方向1 2 4 8

BFS解法（数组模拟队列）

#include
#define x first
#define y second
using namespace std;
const int N = 50;
const int M = N * N;
int g[N][N];
typedef pair<int, int> PII;
PII q[M];
bool st[N][N];
int n, m;
//左上右下
int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};
int bfs(int xx, int yy) {
    //初始化
    int hh = 0, tt = 0;
    int area = 0;
    q[0] = {xx, yy};
    
    //已经搜过的点改为true
    st[xx][yy] = true;
    
    while (hh <= tt) {
        auto t = q[hh++];
        area++;
        for (int i = 0; i < 4; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= m) continue;
            if (st[a][b]) continue;
            if (g[t.x][t.y] >> i & 1) continue;
            q[++tt] = {a, b};
            st[a][b] = true;
        }
    }
    return area;
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    int cnt = 0, area = 0;
    for (int i = 0 ;i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (!st[i][j]) {
                area = max(area, bfs(i, j));
                cnt++;
            }
        }
    }
    cout << cnt << endl;
    cout << area << endl;
    return 0;
}

BFS解法 STL队列

#include
#define x first
#define y second
using namespace std;
const int N = 50;
const int M = N * N;
int g[N][N];
queue<pair<int, int>> q;
bool st[N][N];
int n, m;
//左上右下
int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0};
int bfs(int xx, int yy) {
    //初始化
    int area = 0;
    q.push({xx, yy});
    st[xx][yy] = true;
    
    while (q.size()) {
        auto t = q.front();
        area++;
        for (int i = 0; i < 4; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= m) continue;
            if (st[a][b]) continue;
            if (g[t.x][t.y] >> i & 1) continue;
            q.push({a, b});
            st[a][b] = true;
        }
        q.pop();
    }
    return area;
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    int cnt = 0, area = 0;
    for (int i = 0 ;i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (!st[i][j]) {
                area = max(area, bfs(i, j));
                cnt++;
            }
        }
    }
    cout << cnt << endl;
    cout << area << endl;
    return 0;
}

AcWing 1106. 山峰和山谷

链接：Click here~~

八连通

山峰：只要周围没有比它高的

山谷：只要周围没有比它低的

如果周围有比它高也有比它低的就 既不是山峰也不是山谷

如果全部高度一样，那么就 既是山峰也是山谷

解法：在做Flood Fill的时候，判断当前格子和它周围格子的关系，在往外扩展的时候，判断一下扩展的格子，如果不属于当前连通块的话，就标记一下这个格子是比当前格子高还是矮。根据这个条件判断出来，每个连通区域是山峰还是山谷

#include
#define x first
#define y second
using namespace std;
const int N = 1010;
const int M = N * N;
int h[N][N];
bool st[N][N];
typedef pair<int, int> PII;
PII q[M];
int n;
void bfs (int xx, int yy, bool& high, bool& low) {
    int hh = 0, tt = 0;
    q[0] = {xx, yy};
    st[xx][yy] = true;
    
    while (hh <= tt) {
        auto t = q[hh++];
        
        for (int i = t.x - 1; i <= t.x + 1; i++) {
            for (int j = t.y - 1; j <= t.y + 1; j++) {
                if (i < 0 || i >= n || j < 0 || j >= n) continue;
                if (h[i][j] != h[t.x][t.y]) {
                    if (h[i][j] > h[t.x][t.y]) high = true;
                    else low = true;
                } else {
                    if (!st[i][j]) {
                        q[++tt] = {i, j};
                        st[i][j] = true;
                    }
                }
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> h[i][j];
        }
    }
    
    int peak = 0, valley = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (!st[i][j]) {
                bool high = false, low = false;
                bfs(i, j, high, low);
                if (!high) peak++;
                if (!low) valley++;
            }
        }
    }
    cout << peak << ' ' << valley << endl;
    return 0;
}

最短路模型

当所有边的权重相等的时候，用bfs从起点开始搜，当第一次搜索到的时候，这个路径就是最短路，称作（单源最短路）

AcWing 1076. 迷宫问题（单源最短路）(二维)

链接：Click here~~

题解：找到一条最短路径，从(0,0)到(n-1,n-1)，简单的一个bfs

#include
using namespace std;
#define x first
#define y second
const int N = 1010;
const int M = N * N;
typedef pair<int, int> PII;
int n;
int g[N][N];
PII q[M];
PII pre[N][N];//存路径
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void bfs(int xx, int yy) {
    int hh = 0, tt = 0;
    q[0] = {xx, yy};
    memset(pre, -1, sizeof pre);
    //起点无所谓，随便弄个数都可以，只要不是-1，就是证明这个点已经走过了。
    pre[xx][yy] = {0, 0};
    while (hh <= tt) {
        PII t = q[hh++];
        for (int i = 0; i < 4; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= n) continue;
            if (g[a][b]) continue;//如果是墙
            if (pre[a][b].x != -1) continue;
            q[++tt] = {a, b};
            pre[a][b] = t;//记录上一步的状态
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> g[i][j];
        }
    }
    
    bfs(n - 1, n - 1);//因为路径存储是反向存储的，现在需要正向输出，所以从终点开始搜索的话就可以不用多用一个数组记录答案路径
    PII end(0, 0);
    
    while (true) {
        cout << end.x << ' ' << end.y << endl;
        //如果搜索到起点了，就中止循环
        if (end.x == n - 1 && end.y == n - 1) break;
        end = pre[end.x][end.y];
    }
    return 0;
}

POJ 2251 Dungeon Master （三维迷宫问题）

#include
#include
#include
#include
#include
using namespace std;
const int N = 30;
char g[N][N][N];//迷宫地图
bool st[N][N][N];//判断是否走过
struct node {
    int x, y, z;
    int steps;
};
struct node s, e;
int l, r, c;
 //三维bfs
int bfs() {
	int dx[6] = {-1, 0, 0, 1, 0, 0};
	int dy[6] = {0, -1, 0, 0, 1, 0};
	int dz[6] = {0, 0, -1, 0, 0, 1};
    queue<node> q;
    q.push(s);
    st[s.x][s.y][s.z] = true;
    //如果队列不空入队
    while (!q.empty()) {
        struct node t = q.front();
        if (g[t.x][t.y][t.z] == 'E') return t.steps;
        
        //枚举6个方向
        for (int i = 0; i < 6; i++) {
        	struct node tt;
            tt.x = t.x + dx[i], tt.y = t.y + dy[i], tt.z = t.z + dz[i];
            //以这个方向行走后所得到的新的坐标 
			tt.steps = t.steps + 1;
			
			if (tt.x < 0 || tt.x >= r || tt.y < 0 || tt.y >= c || tt.z < 0 || tt.z >= l) continue;
			if (g[tt.x][tt.y][tt.z] == '#') continue;
			if (st[tt.x][tt.y][tt.z]) continue;
			
			st[tt.x][tt.y][tt.z] = true;
			q.push(tt);
        }
        q.pop();
    }
    return -1;
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
    while (cin >> l >> r >> c) {
        memset(st, 0, sizeof st);
        if (l == 0 && r == 0 && c == 0) break;
        for (int i = 0; i < l; i++) {
            for (int j = 0; j < r; j++) {
                for (int k = 0; k < c; k++) {
                    cin >> g[j][k][i];
                    if (g[j][k][i] == 'S') {
                        s.x = j; s.y = k; s.z = i;
                    }
                }
            }
        }
        int res = bfs();//进行三维BFS 
        if (res != -1) cout << "Escaped in " << res << " minute(s)." << endl; //按照题目中给出的格式输出res
        else cout << "Trapped!" << endl;;//如果无法到达输出"Trapped!"
    }
    return 0;
}

AcWing 188. 武士风度的牛

链接：Click here~~

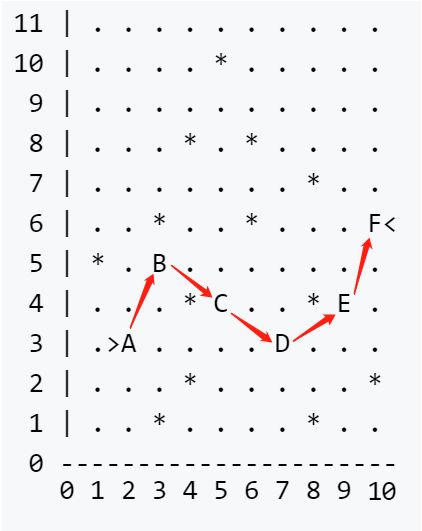
题意：这个牛可以跟中国象棋里面的马相同走法，K为起点，H为终点，问从K跳到H，至少需要跳多少次。

（连通分两种，一种是四连通，一种是八连通）

路径是：A->B->C->D->E->F，总共五步

#include
#define x first
#define y second
using namespace std;
const int N = 155;
const int M = N * N;
char g[N][N];
typedef pair<int, int> PII;
PII q[M];
//记录步数
int dist[N][N];
//定义8个方向
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
int m, n;
int bfs(int xx, int yy) {
    int hh = 0, tt = 0;
    q[0] = {xx, yy};
    memset(dist, -1, sizeof dist);
    dist[xx][yy] = 0;
    while (hh <= tt) {
        PII t = q[hh++];
        for (int i = 0; i < 8; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= m) continue;//判越界
            if (g[a][b] == '*') continue;//此路不通
            if (dist[a][b] != -1) continue;//如果这个地方已经走过了
            if (g[a][b] == 'H') return dist[t.x][t.y] + 1;//如果是H，就是重点，加上这个点的步数就可以了
            q[++tt] = {a, b};
            dist[a][b] = dist[t.x][t.y] + 1;
        }
    }
    return -1;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> m >> n;
    for (int i = 0; i < n; i++) cin >> g[i];
    
    int xx, yy;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            //K 是起点
            if (g[i][j] == 'K') {
                xx = i, yy = j;
            }
        }
    }
    cout << bfs(xx, yy) << endl;
    
    return 0;
}

LUOGU P1443 马的遍历

链接：Click here~~

题意：有一个 $n\times m$ 的棋盘 $1<n,m\le 400$ ，在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。

题解：

最短路模型的模板题，BFS第一次走到的就是最短路径

#include
#define x first
#define y second
using namespace std;

const int N = 410;

//方向：上右下左
int dx[10] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
int dy[10] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
int n, m, xx, yy;
int dist[N][N];//存距离
typedef pair<int, int> PII;
queue<PII> q;

void bfs(int xx, int yy) {
	memset(dist, -1, sizeof dist);
	dist[xx][yy] = 0;//初始化起点
	q.push({xx, yy});//起点入队
	while (q.size()) {
		PII t = q.front();
		for (int i = 1; i <= 8; i++) {
			int a = t.x + dx[i], b = t.y + dy[i];
            //如果当前点没有越界且没有遍历过，则需要更新
			if (a >= 1 && a <= n && b >= 1 && b <= m && dist[a][b] == -1) {
				dist[a][b] = dist[t.x][t.y] + 1;
				q.push({a, b});
			}
		}
		q.pop();
	}
}
int main () {
	scanf("%lld%lld%lld%lld", &n, &m, &xx, &yy);
	bfs(xx, yy);
	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			printf("%-5d", dist[i][j]);
		}
		printf("\n");
	}
	return 0;
} 

POJ 3278 “Catch That Cow”

多源BFS

适用于有多个起点的搜索题。

AcWing 173. 矩阵距离

链接：Click here~~

题意：给一个n行m列的01矩阵，求出每个点到1的最近曼哈顿距离（行+列）。

将所有源点加入到队列，求出所有多源起点到所有点的最短距离，多源BFS跟普通的BFS相比，区别只是，刚开始需要将所有的起点先放到队列里面去，然后后面就跟普通的BFS相同即可。

如果给出的01矩阵是

0 0 0 1
0 0 1 1
0 1 1 0

最终的结果是：

3 2 1 0
2 1 0 0
1 0 0 1

#include
#define x first
#define y second
using namespace std;
const int N = 1010;
const int M = N * N;
int n, m;
char g[N][N];
typedef pair<int, int> PII;
PII q[M];
int dist[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void bfs(){
    memset(dist, -1, sizeof dist);
    int hh = 0, tt = -1;
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (g[i][j] == '1') {
                dist[i][j] = 0;
                q[++tt] = {i, j};
            }
        }
    }
    while (hh <= tt) {
        auto t = q[hh++];
        for (int i = 0; i < 4; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            
            //出界
            if (a < 0 || a >= n || b < 0 || b >= m) continue;
            if (dist[a][b] != -1) continue;
            
            dist[a][b] = dist[t.x][t.y] + 1;
            q[++tt] = {a, b};
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 0; i < n; i++) cin >> g[i];
    bfs();
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m ;j++) {
            cout << dist[i][j] << ' ';
        }
        cout << endl;
    }
    return 0;
}

最小步数模型

假设对棋盘进行操作，把每一个棋盘，看成一个状态，对棋盘进行操作，操作完后变成一个新的棋盘，求当前棋盘变成目标棋盘所需要的最小步数。

最小步数模型 VS 最短路模型

最短路模型：在棋盘内部去搜索路线。

最小步数模型：把棋盘看成一个点，求至少要进行多少步操作，让这个点变成另一种点。

AcWing 1107. 魔板

链接：Click here~~

从一种状态到另一种状态的最小转化步数就是最小步数模型

pre 来记录当前状态的前置状态

看看题目，主要是这3个操作看起来比较复杂，其实题目挺简单的，注意一下字典序指的是: ABC 这个顺序

#include 
#include 
#include 
#include 
#include 

using namespace std;

char g[2][4];

unordered_map<string, int> dist;//每个状态需要的步数
//每个状态是由什么状态 且执行A、B、C中的哪个操作转移过来的，例如 pair 
unordered_map<string, pair<char, string>> pre;
queue<string> q;

string start = "12345678";

//将字符串放进 2 ×4的矩阵中 
void set(string k) {
    //将前 4个数字放进 2 × 4 的矩阵 
    for (int i = 0; i < 4; i ++ ) g[0][i] = k[i];

    //将后 4个数字放进 2 × 4 的矩阵
    for (int i = 3, j = 4; i >= 0; i--, j++ ) g[1][i] = k[j];
}

//将2 × 4矩阵转成字符串
string get() {
    string res;
    for (int i = 0; i < 4; i++) res += g[0][i];
    for (int i = 3; i >= 0; i--) res += g[1][i];
    return res;
}

//执行A操作
string turnA(string k) {
    set(k);
    for (int i = 0; i < 4; i ++ ) swap(g[0][i], g[1][i]);
    return get();
}

//执行B操作
string turnB(string k) {
    set(k);
    char v0 = g[0][3], v1 = g[1][3];
    g[0][3] = g[0][2];
    g[0][2] = g[0][1];
    g[0][1] = g[0][0];
    g[0][0] = v0;

    g[1][3] = g[1][2];
    g[1][2] = g[1][1];
    g[1][1] = g[1][0];
    g[1][0] = v1;

    return get();
}

//执行C操作
string turnC(string k) {
    set(k);
    char v = g[0][1];
    g[0][1] = g[1][1];
    g[1][1] = g[1][2];
    g[1][2] = g[0][2];
    g[0][2] = v;
    return get();
}

void bfs(string end) {
    if (start == end) return;
    q.push(start);
    dist[start] = 0;

    while (q.size()) {
        auto t = q.front();
        q.pop();

        string m[3];
        m[0] = turnA(t);
        m[1] = turnB(t);
        m[2] = turnC(t);

        for (int i = 0; i < 3; i ++) {
            if (!dist.count(m[i])) {
                string str = m[i];
                dist[str] = dist[t] + 1;
                pre[str] = {'A' + i, t};
                q.push(str);
                if (str == end) return;
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int x;
    string end;
    for (int i = 0; i < 8; i ++) {
        cin >> x;
        end += char(x + '0');
    }

    bfs(end);

    cout << dist[end] << endl;

    string res;
    while (end != start) {
        res += pre[end].first;
        end = pre[end].second;
    }

    reverse(res.begin(), res.end());

    if (res.size()) cout << res << endl;

    return 0;
}

双端队列广搜

要求最小值，不能只在队尾插入，还需要在队首插入

AcWing 175. 电路维修

链接：Click here~~

双向广搜

BFS可以想象成在一个平静的池塘丢一颗石头，波浪一层一层的向外扩散，直到搜到目标，第一次搜到目标的路径就是最优路径。那么如果同时在起点和终点同时丢一颗石头，两颗石头产生的波浪都向对方扩散，在某个位置中相遇，此时得到了最优路径。

从图解上看：

从数据上看：

假设单向BFS的数据是：$6^{10}=60466176$

则双向BFS的数据则是：$2\times 6^5=15552$

一般双向BFS解决的问题是在最小步数模型里面。

在最短路模型和Flood Fill里面一般用不到，因为在这两种模型中，搜到的点一般不大，因此直接搜也是可以的

在最小步数模型，整个状态空间数量一般是指数级别的，用双向广搜可极大提升效率

####HDU 1401. Solitaire （待更新）

题意：有一个8 × 8的棋盘，上面有4颗棋子，棋子可以上下左右移动。给定一个初始状态

HDOJ 3085 Nightmare Ⅱ（待更新）

AcWing 190. 字符变换（代码待更新）

题意：给出两个字串A、B和字符变换规则（至多6个）其中（$A_1\to B_1$ 表示在A中子串 $A_1$ 可以变成 $B_1$）

例子：

A1 = "abcd"   B1 = "xyz"
规则：
Ⅰ. abc → xu
Ⅱ. ud → y
Ⅲ. y → yz
则abcd → xud → xy → xyz 

要求：在10步内，求A变成B，输出最少变换次数

最坏的情况下：如果用一般的BFS 20(起点) × 6(变换规则) → 变换10次 $ (20 × 6)^{10}$

所以如果用一般的BFS会容易TLE

A*算法（待更新）

$A\ast$算法也是一种在图中求解最短路径问题的算法，由Dijkstra算法发展而来，Dijkstra算法会从离起点近的顶点开始，按顺序求出起点到各个顶点的最短路径。也就是说，一些离终点较远的顶点的最短路径也会被计算出来，但这部分其实是无用的。与之不同，$A\ast$ 就会先估算一个值（从起点到终点的距离）并利用这个值省去一些无用的计算。

AcWing 178. 第K短路

AcWing 179. 八数码

DFS

DFS —— 不撞南墙不回溯 —— 死脑筋

DFS	BFS
stack（栈）	queue（队列）
$O(h)$	$O(2^h)$
不具有最短路性质	具有最短路性质

DFS例题

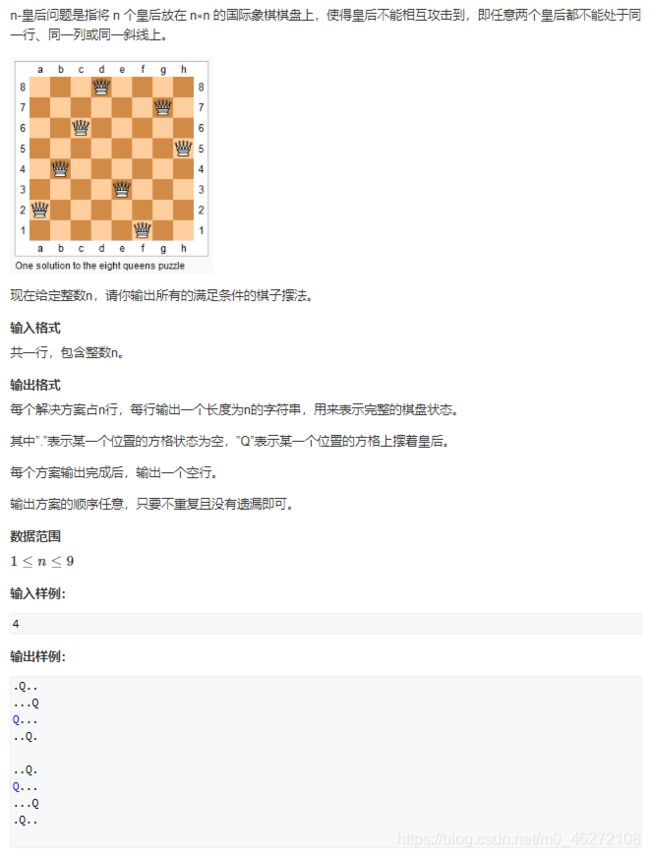
给定一个整数n，将数字1~n排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围

$1\le n\le 7$

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

DFS的路线图：

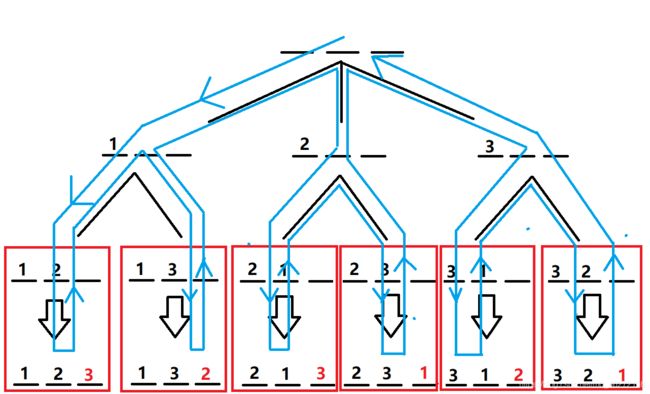
我们不需要存这个树，每次深搜走到底就是一条路线。

回溯的过程中需要注意：恢复原样。

代码（爆搜）：

C++代码实现

#include
using namespace std;

const int N = 10;
int n;
int path[N];//保存路径
bool flag[N];
void dfs(int u)//u代表层数，u==n的时候就是叶节点。
{
	if (u == n)
	{
		for (int i = 0; i < n; i++)
			printf("%d ", path[i]);
		puts("");//输出空行
		return;
	}

	for (int i = 1; i <= n; i++)
	{
		if (!flag[i])//如果当前这个数没有被用过
		{
			path[u] = i;//填写i
			flag[i] = true;
			dfs(u + 1);//进入下一层递归，递归函数之后记得要恢复原状
			flag[i] = false;//回溯之后需要恢复原样
		}
	}
}
int main()
{
	cin >> n;
	dfs(0);
	return 0;
}

Java代码实现

import java.util.Scanner;
public class Main {
    static int n;
    static int[] path;//保存路径
    static boolean[] flag;//打标记
    //u代表层数，u == n的时候就是叶节点
    public static void dfs(int u) {
        if (u == n) {
            for (int i = 0; i < n; i++) {
                System.out.print(path[i] + " ");
            }
            System.out.println();
            return;
        }
        for (int i = 1; i <= n; i++) {
            //如果这个数没有被用过
            if (!flag[i]) {
                path[u] = i;//填写i
                flag[i] = true;
                dfs(u + 1);//进入到下一层递归，递归函数之后记得要恢复原状
                flag[i] = false;//回溯之后需要恢复原样
            }
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        path = new int[n];
        flag = new boolean[n + 1];
//        long startTime = System.currentTimeMillis();
        dfs(0);
//        long endTime = System.currentTimeMillis();
//        System.out.println("运行时间:" + (endTime - startTime) + "ms");
    }
}

牛客小白月赛15 E.小雨的矩阵

题解：爆搜求从起点到终点有多少种路径和。
开一个st数组存储当前路径的点权和是否已经存在。

#include
#define ll long long
#define int ll
#define INF 0x3f3f3f3f
#define PI acos(-1)
using namespace std;
const int N = 10;
int n;
int g[N][N];
bool st[1000];
void dfs(int x, int y, int sum) {
	sum += g[x][y];
	if (x == n && y == n) {
		st[sum] = true;
		return;
	}
	if (x + 1 <= n) dfs(x + 1, y, sum);
	if (y + 1 <= n) dfs(x, y + 1, sum);
}
signed main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= n; ++j) {
			cin >> g[i][j];
		}
	}
	
	dfs(1, 1, 0);
	int ans = 0;
	for(int i = 0; i < 1000; ++i) if (st[i]) ans++;
	cout << ans << endl;
	return 0;
}

在这里插入代码片

八皇后问题（DFS经典问题）

剪枝：提前终止搜索，直接回溯，不用继续往下搜索了。

第一种搜索方式 （全排列思想）：

#include
using namespace std;

const int N = 20;

int n;
char path[N][N];//path代表路径
bool col[N], dg[N], udg[N];//col代表列，dg代表正对角线，udg代表反对角线

void dfs(int row)
{
	//当u==n时，表示已经搜了n行，所以输出这条路径
	if (row == n)
	{
		for (int i = 0; i < n; i++)
			cout << path[i] << endl;
		cout << endl;
		return;
	}

	//当前枚举第u行，看皇后放在哪一列
	for (int i = 0; i < n; i++)
		// 剪枝
		if (!col[i] && !dg[row + i] && !udg[n - row + i])//如果皇后在一列且正反对角线都没有。
		{
			path[row][i] = 'Q';//填写皇后
			col[i] = dg[row + i] = udg[n - row + i] = true;
			dfs(row + 1);
			//回溯之后需要恢复原样
			col[i] = dg[row + i] = udg[n - row + i] = false;
			path[row][i] = '.';

		}
}
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			path[i][j] = '.';//地图上先打满点
	dfs(0);
	return 0;
}

解释一下第24行代码，dg和udg数组下标问题。

第二种搜索方式 ：

#include
using namespace std;

const int N = 20;

int n;
char path[N][N];//path代表路径
bool row[N], col[N], dg[N], udg[N];//row代表行，col代表列，dg代表正对角线，udg代表反对角线

void dfs(int x, int y, int s)
{
	
	if (s > n)
		return;
	if (y == n)
	{
		y = 0;
		x++;
	}
	if(x==n)
	{
		if (s == n)
		{
			for (int i = 0; i < n; i++)
				cout << path[i] << endl;
			cout << endl;
			return;
		}
	}

	path[x][y] = '.';
	dfs(x, y + 1, s);

	if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
	{
		row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
		path[x][y] = 'Q';
		dfs(x, y + 1, s + 1);
		path[x][y] = '.';
		row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
	}
}
int main()
{
	cin >> n;

	dfs(0, 0, 0);

	return 0;
}

DFS之连通性模型

AcWing 1112. 迷宫

链接：Click here~~

做一个简单的DFS

#include
using namespace std;
const int N = 110;
char g[N][N];
bool st[N][N];
int xa, ya, xb, yb;
int n;
bool dfs(int x, int y) {
    if (g[x][y] == '#') return false;
    if (x == xb && y == yb) return true;
    st[x][y] = true;
    
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    
    for (int i = 0; i < 4; i++) {
        int a = x + dx[i], b = y + dy[i];
        if (a < 0 || a >= n || b < 0 || b >= n) continue;
        if (st[a][b]) continue;
        if (g[a][b] == '#') continue;
        st[a][b] = true;
        if (dfs(a, b)) return true;
    }
    return false;
}
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int t;
    cin >> t;
    while (t--) {
        cin >> n;
        for (int i = 0; i < n; i++) cin >> g[i];
        
        memset(st, false, sizeof st);
        
        cin >> xa >> ya >> xb >> yb;
        if (dfs(xa, ya)) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
    return 0;
}

Luogu P1605 迷宫

链接：Click here~~

题解：四连通，建图，先将所有的点初始化为1，如果是障碍的话，就把当前障碍的点改为0，然后做一个简单的DFS。

#include
using namespace std;
const int N = 10;

int g[N][N];
bool st[N][N];
 
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};

int cnt;
int sx, sy, ex, ey;
int n, m, t;

int l, r;
void dfs(int xx, int yy) {
	if (xx == ex && yy == ey) {
		cnt++;
		return;
	} else {
		for (int i = 0; i < 4; i++) {
			int a = xx + dx[i], b = yy + dy[i];
			if (g[a][b] == 1 && !st[a][b]) {
				st[xx][yy] = true;
				dfs(a, b);
				st[xx][yy] = false;
			}
		}
	}
} 

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> n >> m >> t;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			g[i][j] = 1;
		}
	}
	cin >> sx >> sy >> ex >> ey;
	
	while (t--) {
		cin >> l >> r;
		g[l][r] = 0;
	}
	
	dfs(sx, sy);
	cout << cnt;
	return 0;
}

AcWing 1113. 红与黑

链接：Click here~~

#include
using namespace std;
const int N = 25;
char g[N][N];
bool st[N][N];
int n, m;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//上右下左四个方向
int dfs(int x, int y) {
    int cnt = 1;
    g[x][y] = '#';
    for (int i = 0; i < 4; i++) {
        int a = x + dx[i], b = y + dy[i];
        if (a < 0 || a >= n || b < 0 || b >= m) continue;
        if (g[a][b] != '.') continue;
        st[a][b] = true;
        cnt += dfs(a, b);
    }
    return cnt;
}
int main()
{
    while (cin >> m >> n && n && m) {
        for (int i = 0; i < n; i++) cin >> g[i];
        
        int x, y;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                //起点
                if (g[i][j] == '@') {
                    x = i, y = j;
                }
            }
        }
        cout << dfs(x, y) << endl;
    }
    return 0;
}

Luogu P1101 单词方阵

链接：Click here~~

连通性的一个问题，在第11届蓝桥杯（省赛）也有一个搜索2020的个数，这个是搜索 “yizhong” 这个字符串的个数，并输出相应位置。

#include
using namespace std;
const int N = 110;
const int dx[] = {-1, -1, 0, 1, 1, 1, -1, 0};
const int dy[] = {0, 1, 1, 1, 0, -1, -1, -1};
int n;
char g[N][N];
char A[N][N];
const string cmp = "yizhong";
void dfs(int x, int y) {
	//搜8个方向 
	for (int i = 0; i < 8; i++) {
		int f = 1;
		//搜一个方向的时候要搜完整个单词 
		for (int j = 1; j <= 6; j++) {
			int a = x + j * dx[i], b = y + j * dy[i];
			//判断越界 
			if (a < 1 || a > n || y < 1 || y > n) {
				f = 0;
				break;
			}
			if (cmp[j] != g[a][b]) {
				f = 0;
				break;
			}
		}
		if (f == 0) continue;
		for (int j = 0; j <= 6; j++) {
			int a = x + j * dx[i], b = y + j * dy[i];
			A[a][b] = g[a][b];
		}
	}
	return;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> g[i][j];
		}
	}
	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (g[i][j] == 'y') dfs(i, j);
		}
	}
	
	for (int i =1 ; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (A[i][j] == 0) A[i][j] = '*';
			cout << A[i][j];
		} 
		cout << endl;
	}
	return 0;
}

DFS之搜索顺序

搜索变量的两个经典顺序：

1. 每次枚举当前剩余选择最少的变量（每次）
2. 每次枚举对后面影响最大的变量（出现在最多的未被满足的约束里)
3. 具体问题具体分析。

AcWing 1116. 马走日

链接：Click here~~

注意方向数组要满足马走日的坐标即可，也是一个简单的DFS而已

#include
using namespace std;
const int N = 10;
bool st[N][N];
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
int ans, cnt;
int n, m, x, y;
void dfs(int x, int y) {
    if (cnt == n * m) {
        ans++;
        return;
    }
    st[x][y] = true;
    for (int i = 0; i < 8; i++) {
        int a = x + dx[i], b = y + dy[i];
        if (a < 0 || a >= n || b < 0 || b >= m) continue;
        if (st[a][b]) continue;
        cnt++;
        dfs(a, b);
        cnt--;
    }
    st[x][y] = false;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--) {
        cin >> n >> m >> x >> y;
        ans = 0;
        cnt = 1;
        dfs(x, y);
        cout << ans << endl;
    }

    return 0;
}

AcWing 1117. 单词接龙

链接：Click here~~

#include
using namespace std;
const int N = 21;

int n;
string word[N];
int g[N][N];//记录wordA的后缀与wordB的前缀长度重叠部分最小的长度是多少
int used[N];//每个单词当前用了多少次
int ans;

// last：上一个单词的编号
void dfs(string dragon, int last) {
    ans = max((int)dragon.size(), ans);
    used[last] ++;//上一个单词用了一次
    for (int i = 0; i < n; i++) {
        if (g[last][i] && used[i] < 2) 
            dfs(dragon + word[i].substr(g[last][i]), i);
    }
    
    used[last]--;
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> word[i];
    char start;//开头的字母
    cin >> start;
    //初始化：判断某个单词是否能接到另外一个单词后面去
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            string a = word[i], b = word[j];
            //求重叠部分，0≤重叠部分≤单词A和单词B的最小长度，重叠部分越小越好，所以是从小到大枚举
            for (int k = 1; k < min(a.size(), b.size()); k++) {
                //判断A的后k个字母，B的前k个字母是不是一样
                if (a.substr(a.size() - k, k) == b.substr(0, k)) {
                    g[i][j] = k;
                    break;
                }
            }
        }
    }
    
    for (int i = 0; i < n; i++) {
        //以start这个字母开头的才可以
        if (word[i][0] == start) {
            dfs(word[i], i);
        }
    }
    
    cout << ans << endl;
    return 0;
}

AcWing 1118. 分成互质组(待更新)

DFS之剪枝与优化

剪枝：在搜索的过程中，可以通过某种条件判断，当前节点所在的子树均不满足要求，便可以不再往下搜索。
剪枝通常比较难估算时间复杂度，因为每一种情况的剪枝都有可能不同。

1. 优化搜索顺序：大部分情况下，优先搜索分支较少的节点
2. 排除等效冗余
3. 可行性剪枝
4. 最优性剪枝

AcWing 165. 小猫爬山

链接：Click here~~

1. 优化搜索顺序：分支较少的节点，限定了缆车的承重，先放重的猫，分支少。
2. 排除等效冗余：无冗余
3. 可行性剪枝：选择这个分支，当前这个格子枚举的数字，不能与所在的行，所在的列，所在的九宫格，有重复。
4. 最优性剪枝：无，因为本体是找可行性方案，不是找最优方案。

#include
using namespace std;
const int N = 20;
int n, m;
int w[N];
int sum[N];
int ans = 18;

void dfs(int cur, int cnt) {
    if (cnt >= ans) return;
    if (cur == n) {
        ans = cnt;
        return;
    }
    
    for (int i = 0; i < cnt; i++) {
        //可行性剪枝
        if (sum[i] + w[cur] <= m) {
            sum[i] += w[cur];
            dfs(cur + 1, cnt);
            sum[i] -= w[cur];
        }
    }
    sum[cnt] = w[cur];
    dfs(cur + 1, cnt + 1);
    sum[cnt] = 0;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    
    for (int i = 0; i < n; i++) cin >> w[i];
    
    dfs(0, 0);
    
    cout << ans << endl;
    return 0;
}

AcWing 166. 数独 (代码有点复杂，等写一下注释再上传)

链接：Click here~~

首先考虑爆搜解题过程：随意选择空格子，填数，选取合适的方案

剪枝优化：

1. 优化搜索顺序：分支较少的节点，选择分支最少的格子，例：如果当前格子能填 1~9任何一个数字，另一个格子能填1、2两个数字，那么自然是先选后者，这样子形成的分支会少。
2. 排除等效冗余：一个个放的话，不会产生等效冗余
3. 可行性剪枝：在当前各自枚举数字，判断不能与所在行，所在列，所在九宫格内已有的数字相同
4. 最优性剪枝：本题因为是求可行性方案，不是求最优性方案，所以没有最优性剪枝。

本题有个特殊的位运算优化：

   行:1 2 3 4 5 6 7 8 9
      0 1 0 0 1 1 1 0 0
   列:1 2 3 4 5 6 7 8 9
      0 1 0 0 1 1 1 0 0
九宫格:1 2 3 4 5 6 7 8 9
	  0 1 0 0 1 1 1 0 0
用二进制来表示当前数字是否已经存在，0表示这个数已经存在，1表示不存在。所以用0~511的二进制数，存储行，列，九宫格已经存在数字的情况。
只有在 行[i]&列[i]&九宫格[i]==1 这个位置就能放这个数字。

在枚举可选数字的时候，如果正常枚举1~9，需要循环9次，可以用 lowbit() 在取二进制数中的最后一个数字，这样当前状态下，有多少个1，就需要循环多少次。 0 1 0 0 1 1 1 0 0 只需要循环4次。

AcWing 167. 木棒

链接：Click here~~

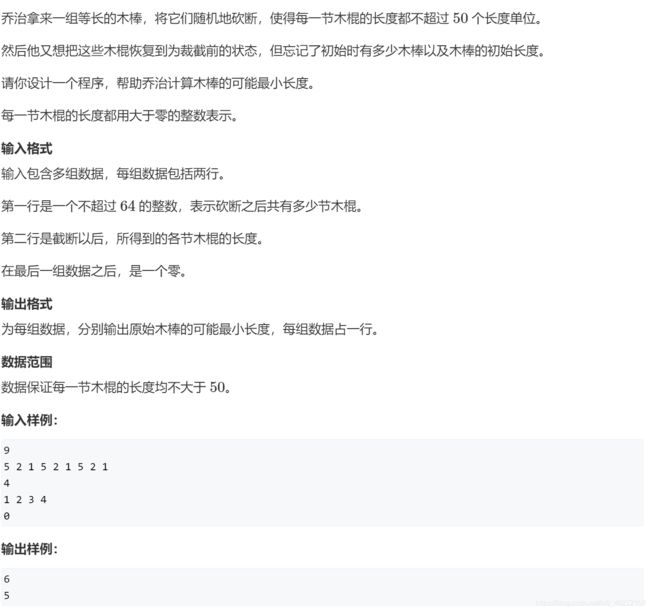
样例：5 2 1 5 2 1 5 2 1
分成4组
5 1
5 1
5 1
2 2 2
长度是6
定义：
木棒：一组等长的木棒
木棍：砍断之后的（题目中输入的数据）

搜索顺序：从前往后依次拼接，一次枚举每根木棒是怎么拼出来的（每根木棒是由哪些木棍拼出来的）将木棒内部木棍排个序，以组合数的形式来枚举木棍（木棍内部顺序是无所谓的，保证总和相等即可）

对于固定长度，如果恰好把所有木棍拼成当前枚举的这个长度，则将此称为合法方案

剪枝：
枚举长度：len
满足：len|sum ，sum一定是len的倍数，只枚举sum的约数即可。

搜索顺序的优化：
先找分支较少的，先枚举较长的木棍

枚举方式： 按组合（不考虑内部顺序）方式枚举，而不是排列（考虑内部顺序）
传一个参数： 表示下一个数的下标从哪个数开始枚举，保证从小到大枚举。

排除等效冗余： （证明如下）

1. 如果当前枚举的木棍失败，那么与当前木棍长度相同的木棍直接忽略。
2. 如果是木棒的第一根木棒拼接失败，则一定失败，直接回溯
3. 如果是木棒的最后一根木棒拼接失败，则一定失败，直接回溯

#include
#include
#include
#include
using namespace std;
const int N = 70;

int n;
int w[N];
int sum;//所有木棍的总和
int len;//枚举木棒的长度
bool st[N];//小木棍有没有被用过

//当前枚举到的木棒，当前木棒的长度，开始的位置
bool dfs(int u, int s, int start) {
    //
    if (u * len == sum) return true;
    //如果当前的木棒长度 == len 则需要开一根新的木棒，木棒数量+1
    if (s == len) return dfs(u + 1, 0, 0);
    
    //枚举每一根木棍
    for (int i = start; i < n; i++) {
        if (st[i]) continue;//如果这个木棍已经枚举过，就pass
        
        //可行性剪枝
        if (s + w[i] > len) continue;//如果当前木棒长度 + 小棍长度 > 枚举木棒的长度，则pass
        
        st[i] = true;   
        //当前这根木棒，木棒长度加上w[i]，开始下标为i+1
        if (dfs(u, s + w[i], i + 1)) return true;
        
        //回溯
        st[i] = false;//恢复现场
        
        if (!s) return false;
        if (s + w[i] == len) return false;
        //剪枝3-2
        int j = i;
        while (j < n && w[j] == w[i]) j++;
        i = j - 1;
        
    }
    return false;
}
int main()
{
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    while (cin >> n && n) {
        memset(st, false, sizeof st);
        sum = 0;
        for (int i = 0; i < n; i++) {
            cin >> w[i];
            sum += w[i];
        }
        
        //优化搜索顺序，从大到小
        sort(w, w + n);
        reverse(w, w + n);
        
        //从小到大枚举木棒的长度
        len = 1;
        while (true) {
            //剪枝1
            //dfs(枚举每一根木棒，当前木棍长度是0，当前下标是0)
            if (sum % len == 0 && dfs(0, 0, 0)) {
                cout << len << endl;
                break;
            }
            len++;
        }
    }
    return 0;
}

AcWing 168. 生日蛋糕（待更新）

迭代加深

概念：迭代加深搜索，实质上就是限定下界的深度优先搜索。即首先允许深度优先搜索K层搜索树，如果没有发现有解4，再将K+1层加入搜索范围，重复执行以上步骤，直至搜到解为止。

解决的问题一般是：搜索树可能很深，但是答案在很浅的位置。

迭代加深是一层层搜的，有点类似BFS

但是迭代加深算法其实是结合了DFS和BFS算法特点的搜索算法。在搜索之前会预设搜索的层数，然后在该层数以内进行DFS，这样子就规避了DFS可能出现的效率低下的问题。

迭代加深也可以说是有条件的DFS，DFS本来是循着一条路一直走下去，直到找到答案或者到叶节点了才会回头，但是这样即使找到答案有可能不是最优，也不是最快的， 甚至有可能会T，尤其是SPJ的题，就很容易T。因此在搜索之前会预设搜索的层数，然后在该层数以内进行DFS，所以适用于当答案处于深度不深的层次时使用。

那么迭代加深相比于BFS好在哪呢？

BFS的空间复杂度是：指数级别的（比较浪费空间）

而迭代加深本质上还是DFS，只会记录某一条路径上的信息，所以是 $O(h)$ 的

那么会不会时间比较长呢？

无容置疑是会的。

迭代加深，假设答案在第3层：

第一次会搜第一层， 第二次会搜第一层和第二层，第三次会搜第一层，第二层，第三层， 前面的节点会被重复搜索。

从实际应用上，迭代加深搜索的效果比较好，并不比BFS慢很多，但是空间复杂度却与BFS相比小很多，在一些层次遍历的题目中，迭代加深也是一种解决的好办法。

AcWing 170. 加成序列

题意：

加成序列：满足这四个条件的序列a被称为“加成序列”：

1. a[1] = 1
2. a[m] = n
3. a[1] < a[2] < a[3] < … < a[m-1] < a[m]
4. 对于每个 $k(2\le k\le m)$ 都存在两个整数 $i$ 和 $j$ $(1\le i,j\le k-1)$ ，使得 a[k] = a[i] + a[j];

题目要求：给定一个整数n，找出符合上述条件的长度m最小的 “加成序列”，答案不唯一，任意输出一个即可。

剪枝1：搜索顺序 —— 优先枚举较大的数

剪枝2：排除等效冗余

在枚举前两个数的和的时候，假设前面有5个数，那么有 $C_5^2+5$ 种选择(5表示，$i$ 和 $j$ 可以相等，可以同时为一个相同的数)。所以在搜索当前层的数时，搜索过的数不会再搜，用布尔数组st存储在该层该数是否被搜过

但是迭代加深的代码还是比较短的：

#include
using namespace std;
const int N = 105;
int p[N];
bool st[N];//用st数组来记录当前的和，是否被计算过，例如 1,4  2,3 如果计算过，1,4 那么就不用计算2,3了
int n;
bool dfs(int cur, int maxdepth) {
    
    if (cur > maxdepth) return false;
    if (p[cur - 1] == n) return true;//最后一个元素为n，代表找到了合法解，返回true
    memset(st, false, sizeof st);
    
    //枚举i和j的和，规定枚举的顺序，按组合数的方式来枚举
    for (int i = cur - 1; i >= 0; i--) {
        for (int j = i; j >= 0; j--) {
            int sum = p[i] + p[j];
            //越界和排除等效冗余
            if (sum > n || sum <= p[cur - 1] || st[sum]) continue;
            st[sum] = true;//这个并不用加一个st[sum]=false;恢复现场st数组只是用来记录sum是否已经被用过，并不是现场的一部分
            p[cur] = sum;
            if (dfs(cur + 1, maxdepth)) return true;
            
        }
    }
    return false;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    p[0] = 1;
    while (cin >> n && n) {
        int depth = 1;
        //当在当前层找不到解的时候，就扩大范围
        while (!dfs(1, depth)) depth++;
        for (int i = 0; i < depth; i++) cout << p[i] << ' ';
        cout << endl;
    }
    
    return 0;
}

双向DFS

比只用单向DFS好的原理：和BFS一样

优化原理：用空间换时间

AcWing 171. 送礼物

链接：Click here~~

1. 将所有物品按重量从大到小排序
2. 先将前K件物品能凑出的所有重量达标。然后排序并判重
3. 搜许哦剩下的N-K件物品的选择方式，然在表中二分出不超过W的最大值。

用空间换时间

分成两段来做dfs

#include
using namespace std;
const int N = 46;
typedef long long ll;
int n, m;
int w[N];//每件物品的重量
int weights[1 << 25];//能凑出物品的重量 2^25
int cnt = 1;//因为0也是可以凑出来的一个重量，所以cnt要从1开始 
int ans = 0;
int k;
//u:当前枚举到哪个数，s:当前的和
void dfs1(int u, int s) {
    if (u == k) {
       weights[cnt++] = s;
       return;
    }
    dfs1(u + 1, s);
    if ((ll)s + w[u] <= m) dfs1(u + 1, s + w[u]);
}

void dfs2(int u, int s) {
    if (u >= n) {
        int l = 0, r = cnt - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if ((ll)s + weights[mid] <= m) l = mid;
			else r = mid - 1; 
        }
        ans = max(ans, weights[l] + s);
        return;
    }
    //分两种情况:
	//1.不选择当前这个物品 
    dfs2(u + 1, s);
    //2.选择当前这个物品 
    if ((ll)s + w[u] <= m) dfs2(u + 1, s + w[u]);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    cin >> m >> n;
    for (int i = 0; i < n; i++) cin >> w[i];
    
    //从大到小，优化搜索顺序
    sort(w, w + n);
    reverse(w, w + n);
    
    k = n / 2 + 2;
    dfs1(0, 0);
    
    sort(weights, weights + cnt);
    cnt = unique(weights, weights + cnt) - weights;
    
    dfs2(k, 0);
    
    cout << ans << endl;
    return 0;
}

IDA*（待更新）

IDA* 指的是:通过估算下界提前剪枝优化后的算法。
IDA* 是以迭代加深DFS的搜索框架为基础，则立即从当前分支回溯
IDA* 还有另外一个名字（迭代加深的A*算法）

把原来简单的深度限制加强为：
若当前深度+未来估计步数>深度限制，则立即从当前分支回溯

AcWing 180. 排书

AcWing 181. 回转游戏

HDU 1560 “DNA sequence”

HDU 1667 “The Rotation Game”

现文约3万字，更新ing