最简单的棋——区字棋和棋证明&&地毯图&&后手不败策略
目录
1.游戏介绍
2.和棋证明
2.1.前期准备
2.2.思路一
2.3.思路二
2.4.思路三
3.地毯图(状态图)
3.1.可行性
3.2.简化地毯图
3.2.1.等效图示意
3.2.2.绘制思路
3.2.3.加强版
3.3.地毯图探索
3.3.1.突破口
3.3.2.成图!!!
4.后手不败策略
1.游戏介绍
这个棋棋盘像区形,所以叫区字棋。这个棋又叫憋死牛棋,跳茅屎坑棋,因为会在区字口画一个圈,如果一方走不了棋,只能把自己的一个棋走到圈里面,即跳进了坑里。这个棋比的是眼疾手快,所以双方棋手约定会越下越快,让对方失误,规则请见下面的视频。
聊聊憋死牛棋_哔哩哔哩_bilibili
注:中间全是我的思考的过程,废话可能有点多,可以直接看最下边的地毯图成图和后手不败策略!!!
2.和棋证明
2.1.前期准备
根据平时的下棋和互联网经验,这个棋如果双方不失误一定是和棋,所以我们要证明是否为和棋。由于一个棋子围不住别人的棋,所以1V1情况不存在;两个棋子很容易围住一个棋子,所以1V2,1的一方一定输棋;只要分析2V2的情况即可,若一方死一个子则该方输棋。
2.2.思路一
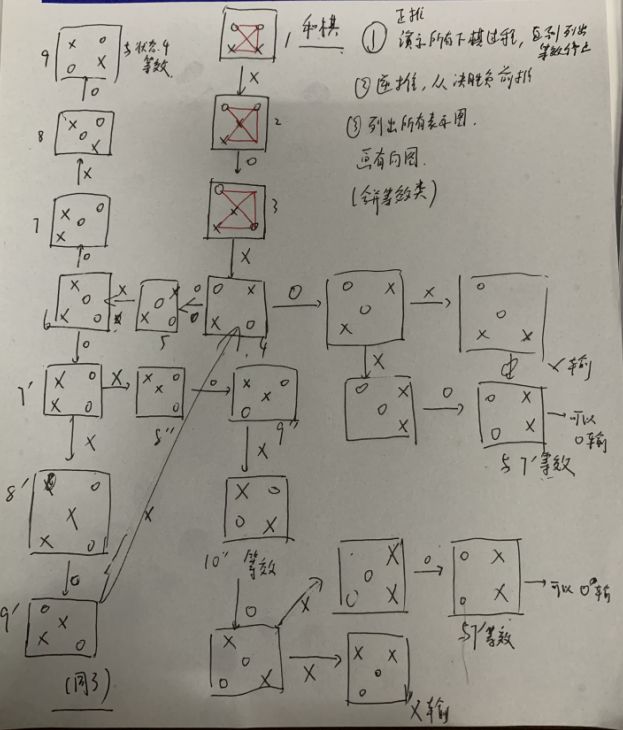
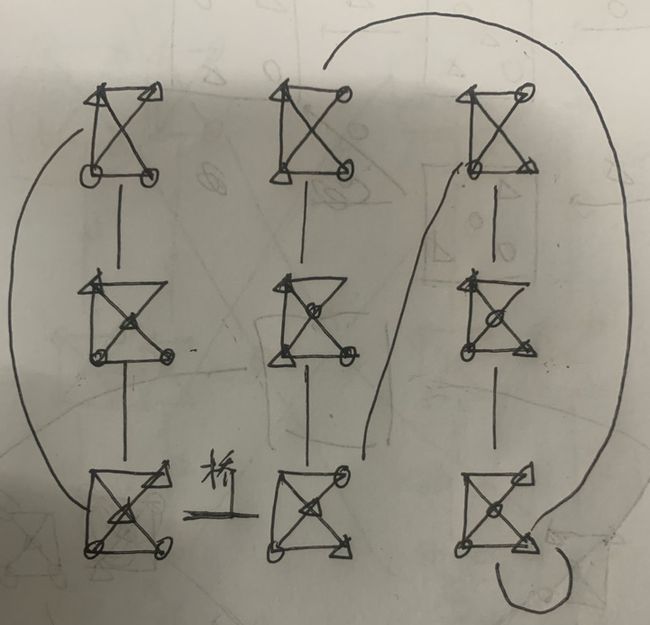
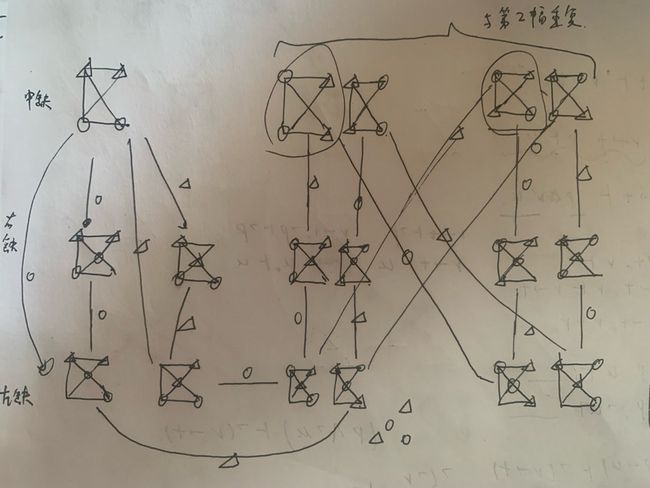
正向列举,演示所有下棋过程,直到列出等效停止。
状态对应图中的点,走棋对应图中的边,XO对应边上的权值,可以看作为01
探索方法类似贪心算法,一个分支探索到头后回到分叉点再探索下一个分支。下面是对这个图的介绍,可以跳过。
我先列举了状态1到状态9,发现状态9与状态4等效(将状态4中的X换成O,O换成X,下一步要走O换为要走X),如果从状态4可以推出X输,则由状态9以类似的方法推出O输。于是我停止了状态9这个分支的探索,因为再探索和状态4之后的路径完全相反,研究完状态4就可以研究完状态9。
接着又列举了状态次7 8 9,发现状态次9下一步又回到了状态4,停止状态次9这个分支的探索。
接着又探索了状态次次8 9 10,发现状态次次10与状态次9图一样,但是下一步不一样,不能算等效。最后的(与次7等效)不对,虽然这两个图与次7相反,但是下一步都要走X,不算等效,当时我觉得次7可以推出X输,与次7相反的图自然能推出O输。
以上图最下方X输的状态及其上一个状态为例,上一个状态还有其他走法避免输的危险,再继续列举,仿佛陷入循环之中。经过深入列举,猜测该棋状态图存在一个大的循环,只要双方都在这个循环之中,则永远不输不赢,而且谁要跳出这个循环谁就输棋。
似乎这已经证明了该棋是和棋,但还有几点疑问。一、有没有方法避免这个循环?二、状态图中存在循环就一定和棋吗?上面只是不完全列举的猜测,需要换其他方法。
2.3.思路二
从决胜负的状态开始前推。但在起点与终点之间存在着一个过不去的循环,可能决策树深度会无限大。还不如把所有状态列出来,画一个完整的状态图。
2.4.思路三
画地毯图(所有情况都列出来的图)。
3.地毯图(状态图)
3.1.可行性
首先憋死牛棋的状态只有 ![]() 种。五个空,放两个X,剩下三个空,放两个O,高中典型排列组合问题。状态很少,足以画全图。
种。五个空,放两个X,剩下三个空,放两个O,高中典型排列组合问题。状态很少,足以画全图。
3.2.简化地毯图
3.2.1.等效图示意
等效原则:通过翻转棋盘或者交换棋子得到的图形一致。
3.2.2.绘制思路
状态寻找
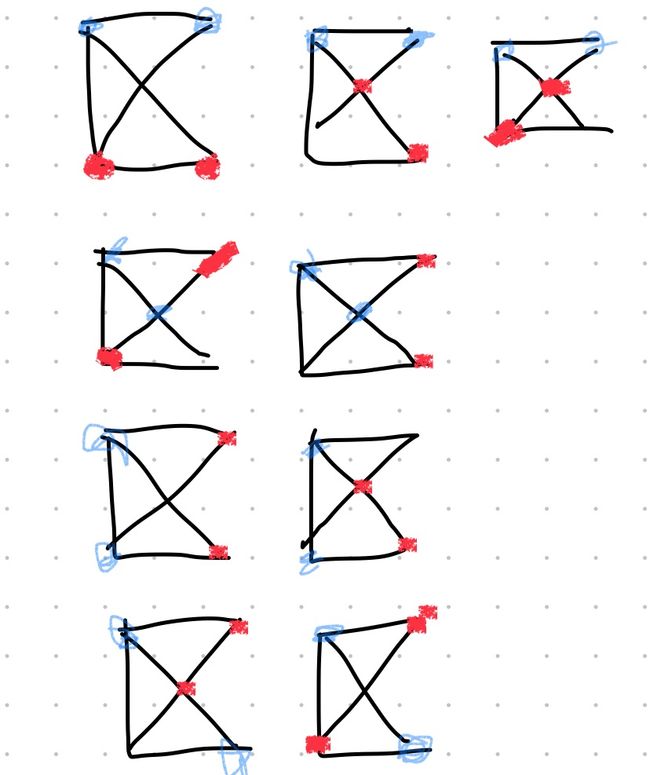
先排好一方的位置(下图是蓝方),再排另一方(红方)的位置,排红方位置时注意交换棋子时的等效情况。
蓝方有四种情况,上图排成了四行。
不过这个方法有个坏处,即蓝方好排,到排红方时每次都要看与前面的图是不是等效,容易出错。我排到最后虽然前面的图没有出错,但是漏了最后一种情况。
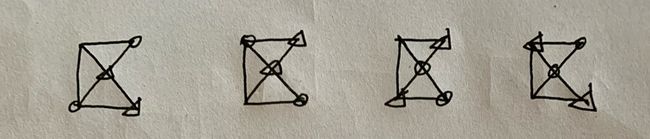
接着我想,既然已经从30种状态化简到9种状态,能不能更进一步?可以,就是不看红蓝色,双方棋子都长得一样,3种情况,分别为左缺、中缺、右缺,就是空位在全图当中的位置在左边、中间还是右边。但只有三种状态,无意义。但这也引出了状态寻找的第二种方法:先把双方棋子看成一样的/或先确定空位的位置,然后再填区分双方的棋子。下图为示例。
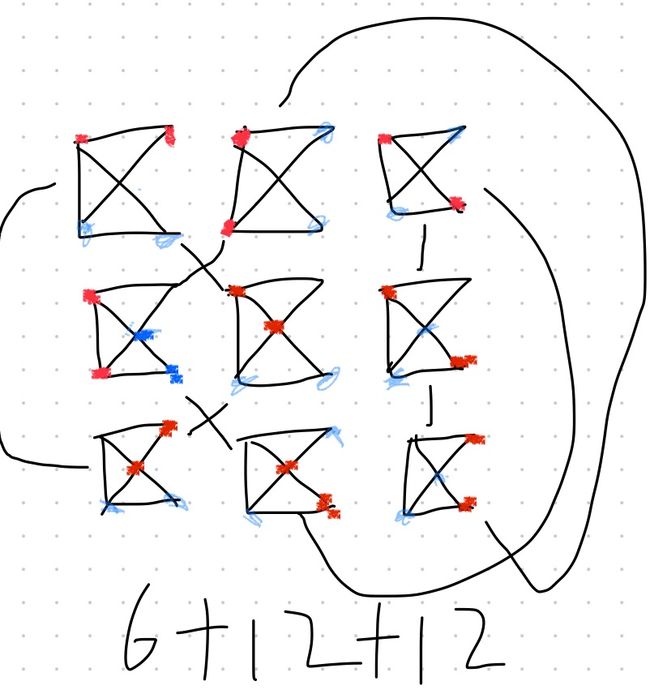
从上到下分别为中缺右缺和左缺。也很容易证出它们对应几种状态。2*3+4*3+4*3=30种状态,合乎前面的推论。我画线时没有考虑两种棋子的差异性和这一条线应该对应哪种棋子走棋。(画状态时考虑了,画线时没考虑)
可以观察,在上图中,左上,左下和中间形成了闭环。剩下的六个状态形成了回环。
在调整之后,简化地毯图如下:(红色用![]() 代替,蓝色用O代替;左中和中间的状态互换)
代替,蓝色用O代替;左中和中间的状态互换)
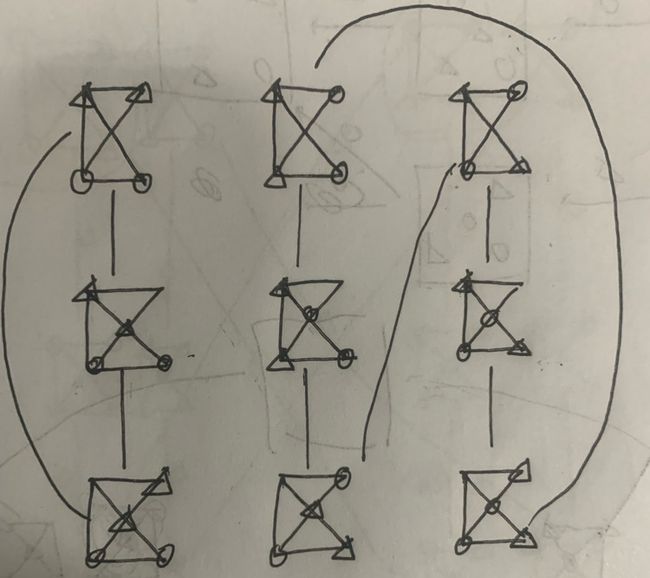
这个图是有缺陷的,最关键的一点不是连通图,但状态图一定是连通图,说明我漏了边。上面和中间两行每个只有两种次态,但下面一行的状态每个有三种次态。(次态怎么找的呢?以左下状态为例,左下的小O和两个![]() 都可以走向左上的空格中,对应三种状态)但我上面的图,最下面三个状态每个都只与两条边相连。修改如下:
都可以走向左上的空格中,对应三种状态)但我上面的图,最下面三个状态每个都只与两条边相连。修改如下:
在左下和中下之间多了条桥,右下本身多了条环。 现在可以通过这个简化的地毯图解释这个棋的一些性质了。
1、循环是没办法避免的。
棋局只能从左上(开始状态)到左下(这里不能到左中,因为第一步先手方不能把对方堵死);然后又只能从左下到中下,(不能回到左上,因为现实棋局不存在此情况,对应到该简化图不存在在两个状态间反复横跳的情况;不能到左中,也是根据下棋的经验,开始时左下回不到左中,但要结束时左下可以回到左中)。中下即进入循环和跳出循环的唯一等效状态(与之有共同功能的一共四个状态)。
2、若要跳出循环,中下所对应的四种状态是必经之地,经过列举,发现有的情况可能决定胜负,有的情况一定不决定。
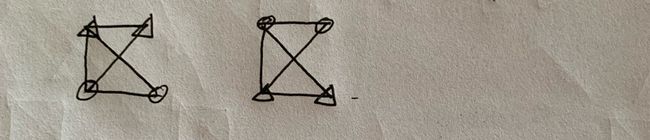
(1)中下对应的四种状态(四种中下状态)
(2)左上对应的两种状态(两种左上状态)
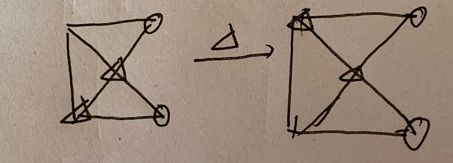
(3)有的情况可能决定胜负(下图圆圈方),有的情况一定不决定(下图三角方)。
如果此时圆圈方走棋,则有两种情况,最左边一种将跳出循环,结束棋局;中间的还是在循环中,结局未知 。若此时三角方走棋,只有一种情况,结局未知。
3.2.3.加强版
接下来就要考虑画全状态图(完整版地毯图)了。一开始我认为完整版地毯图就是4层简化版地毯图,而最上面的状态每一个分状态将独享两层,所以我决定,先画出一层的地毯图,再画其余3层的地毯图,最后画剩下跨层的边。
其中,蓝变红红变蓝是指我右上角的状态红蓝标反了。右上角剩下的字可以不用管。状态周围用蓝笔标上的数字代表该状态是2个图还是4个图的等效。
下图实质是不完全的有向图,还有一条循环线路没有画,即中下->右上->右中->右下->中上->中中->中下;也没有标箭头是谁走的。至于我为什么标“蓝变红红变蓝”,是因为我是按循环箭头顺序构造的右边6个状态,在中上->右下时走错了层次的棋,应该走中上状态中左下角蓝棋,我走了左上角,导致图中右上->中下不对应。//这里也说明了一个问题,但我当时没意识到,即中上是其中一个改变层次的关键。
现在回看,这个思路是正确的,也能画出地毯图,但画出的地毯图是立体的,平面的不直观,而且构造时很容易出错,所以我放弃了从用简化地毯图拼出地毯图的想法。
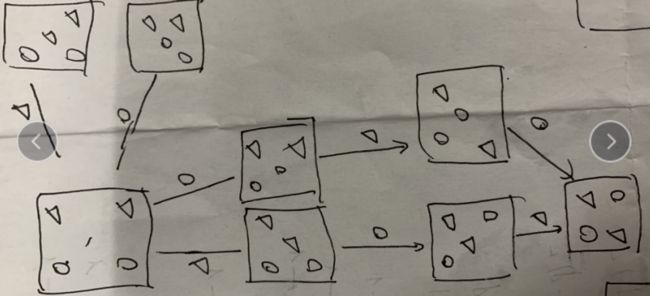
我想过分成四部分再连起来,但这四层地毯图有重合的部分,哪些边需要跨区,哪些边不用,需要验证;也想过合成平面图,下面是两层地毯图合并的情况(第二层画错了),我发现很容易出错,就停止了。
两层地毯图合并平面示意图//这里花的时间很多但没出结果
我构思的立体地毯图长什么样呢?类似两张相同大小以相同方式对折好的纸上下叠起来。两条纸脊即最上层中缺,四个面放入左缺和右缺。跨越层级的边好像毛线,把两叠纸缝起来。
3.3.地毯图探索
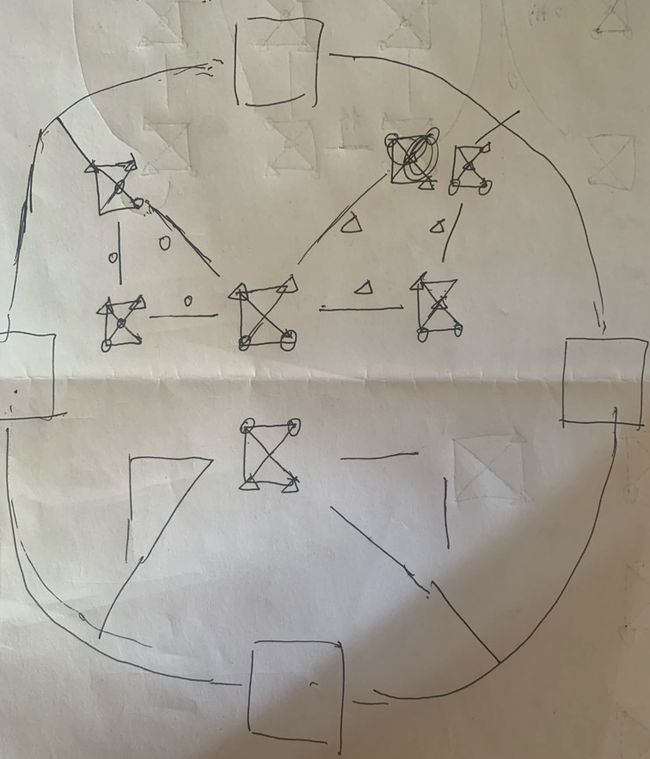
由于之前发现循环部分与剩下的部分只有桥相连,联系并不密切。所以我决定先画出除循环的其他部分。然后把与循环对接的状态看作接口,下图中间部分与外层循环应该有四个桥,四个接口。
我当时猜测四个方框内即四种中上+右上状态。
但因为无法确定循环的形状,特别是无法确定中上和右上在循环中起到的作用,所以又放弃了。
3.3.1.突破口
我开始研究右上状态和中上状态的关系,画出了下图,发现了希望。这个图没标区字口,我也忘了哪个地方是区字口了,不过这不重要,重要的是我发现了四种中上和右上状态的清晰关系,任意一个右上状态与任意一个中上状态之间有两条相同长度且不重合的最短路径,最短路径长度为3。于是我画出了类似圆环的形状,这是成图的框架。
3.3.2.成图!!!
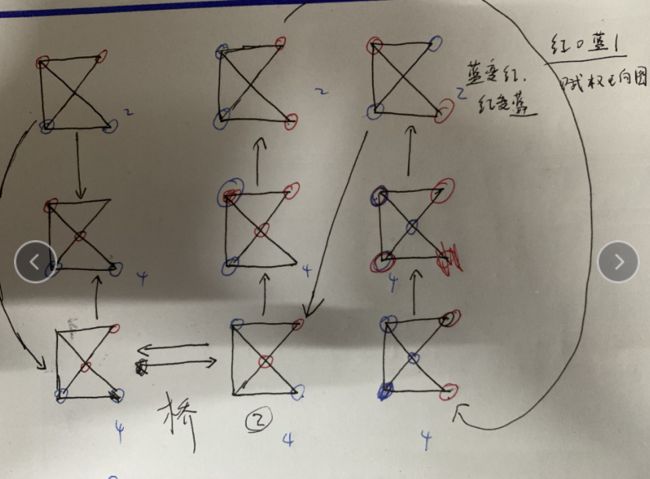
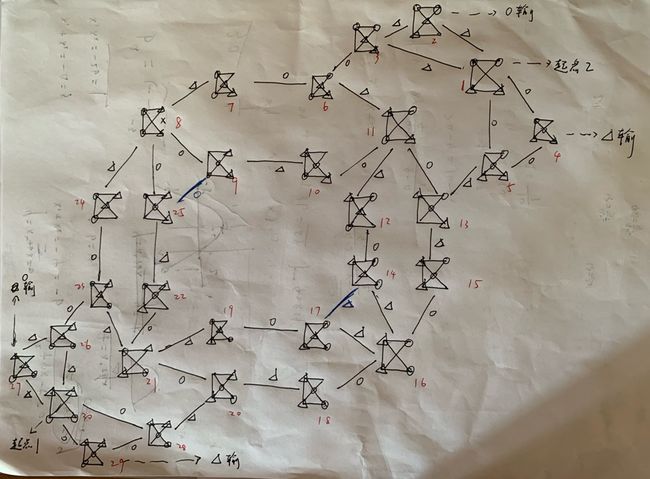
该图有30种状态,42条边,是赋权无向图,权值为圆圈或三角,可以看成0或1。图中的边对应走棋,权值对应是哪一方在走棋。
每种状态我用红笔在旁边写下编号,蓝笔表明了特别重要的两条边(9-25)(14-17),这两条边是简化地毯图中右下状态的环,与后面的后手不败策略有密切的联系。
3.3.2.1.用法
从起点开始走到最终状态,路径必须是O ![]() O
O ![]() 或者
或者![]() O
O ![]() O交替出现,因为规则是双方交替走棋。
O交替出现,因为规则是双方交替走棋。
3.3.2.2.绘制思路
1、画出圆环框架。由3.3.1突破口一节可以类似画出状态8到21,8到11,11到16,21到16四个部分。
2、画出两个起点部分,并用对应的桥(26-23)(28-20)(3-6)(5-13)连接圆环部分。
3、最后连接(9-25)(14-17)两个特殊边。
检查:理论证明该地毯图一共有42条边,可以数一下到底有没有42条就好了。
地毯图有42条边的证明:6种中缺状态,每个状态有四个度;12种右缺状态,每个状态有两个度;12种左缺状态,每个状态有两个度,理论边数:(6*4+12*2+12*3)/ 2 == 42 。
全图花了没有半个小时就搞完了,看来还是正确的思路最重要啊!
4.后手不败策略
前面已经得出一个结论,憋死牛棋进入循环状态后,谁走了跳出循环状态的棋,谁就要输。由地毯图可以清晰看出,跳出循环状态只有四种状态,分别是6,13,20,23,所以双方都要提防这四种状态。但是后手方可以通过一定的策略不用考虑这四种状态。示例如下:
设起点为状态1,先手方为![]() 。路径则为1->3->6,此时6不能到7,因为是
。路径则为1->3->6,此时6不能到7,因为是![]() 走棋,只能6->11。11是O走棋,有两种选择,一种是10,一种是13,先选13吧。11->13,此时
走棋,只能6->11。11是O走棋,有两种选择,一种是10,一种是13,先选13吧。11->13,此时![]() 走棋,要是走向5就输棋了,只能往15走,13->15->16。到16又是
走棋,要是走向5就输棋了,只能往15走,13->15->16。到16又是![]() 走棋,又有两种情况,第一种16->14->12->11,回到11,又是O走棋,陷入循环;第二种16->17->19->21,到21先暂时停一下,因为11->10的路径还没有分析。11->10->9,此时O走棋,O不要往25走,这样会导致攻守之势异形,只能9->8。到8又有两种情况,第一种8->7->6->11又回到了11,第二种8->24->23->21,先停住。问题来了,为什么不能8->7->6->3?为什么不能8->24->23->6?因为路径必须是O
走棋,又有两种情况,第一种16->14->12->11,回到11,又是O走棋,陷入循环;第二种16->17->19->21,到21先暂时停一下,因为11->10的路径还没有分析。11->10->9,此时O走棋,O不要往25走,这样会导致攻守之势异形,只能9->8。到8又有两种情况,第一种8->7->6->11又回到了11,第二种8->24->23->21,先停住。问题来了,为什么不能8->7->6->3?为什么不能8->24->23->6?因为路径必须是O ![]() O
O ![]() 或者
或者![]() O
O ![]() O交替出现!所以O走6->3,23->16都不成立!
O交替出现!所以O走6->3,23->16都不成立!
在上面的例子中,经过归纳,只要O不走9->25或25->9,遇到6、13、20、23这四个危险位置,要么O走不过去,要么![]() 要陷入判断之中!优势一直是O的。只要O走了9->25或25->9,优势翻转。还是以上例为例,路径为1->3->6->11->10->9->25->22->21,这些不变,21->23,O要判断要走24还是26,之后只要
要陷入判断之中!优势一直是O的。只要O走了9->25或25->9,优势翻转。还是以上例为例,路径为1->3->6->11->10->9->25->22->21,这些不变,21->23,O要判断要走24还是26,之后只要![]() 不走(17-14)这条边,优势一直是
不走(17-14)这条边,优势一直是![]() 的。
的。
所以为什么会出现上面的情况呢?因为如果没有(9-25)(17-14)危险位置之间的路径一定是偶数,但这个棋都是你走一步我走一步的,如果这次是我在抉择,那下次一定也还是我在抉择。有一句话形容这个场面非常贴切,这次吃苦,下次还吃苦,永远有吃不完的苦。是的,如果你是劣势方,这个棋是只要对方不犯错,你就有无数次的抉择,直到游戏结束。而(9-25)(17-14)就是起到缩短路径的作用,如果没有(9-25),9到25之间的最短路径为2,但现在是1,进而变换了路径的奇偶性。
总结一下为什么开局后手方优势。
1、思考的局面少,只要不走下图局面,其他情况都不用考虑。//这就是后手不败策略
而先手方要考虑四种危险情况(实际只有两种,状态13和20或6和23,不过它们四个长的太像,下棋考虑不了那么多)。
这个棋有个明显的特点就是越下越快,让别人失误,所以考虑情况越少,越占优势。
2、后手方的危险状态为0种,先手方的危险状态有两种。即便是后手方下错了棋,也不会输,最多是丢了优势;但先手方一旦走错了棋,立马输棋。