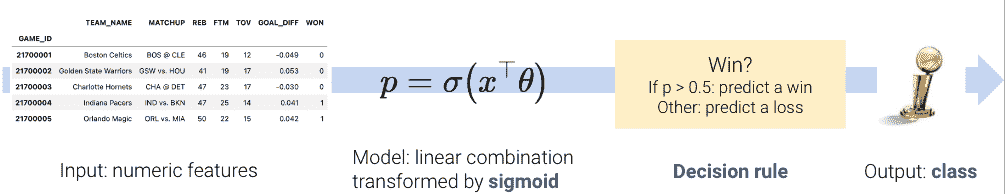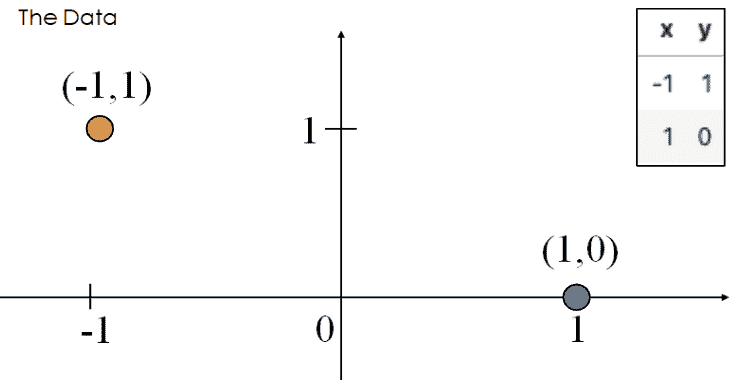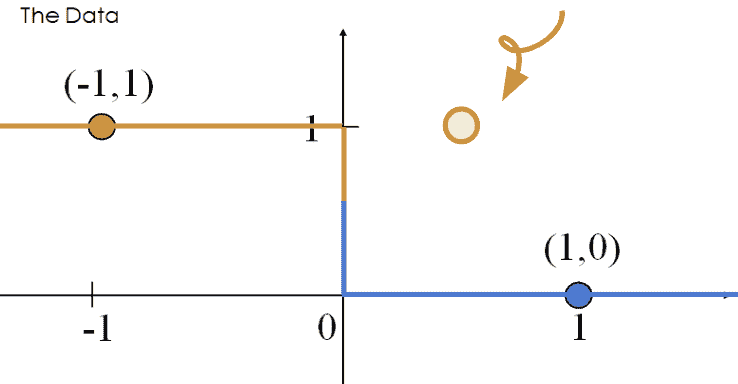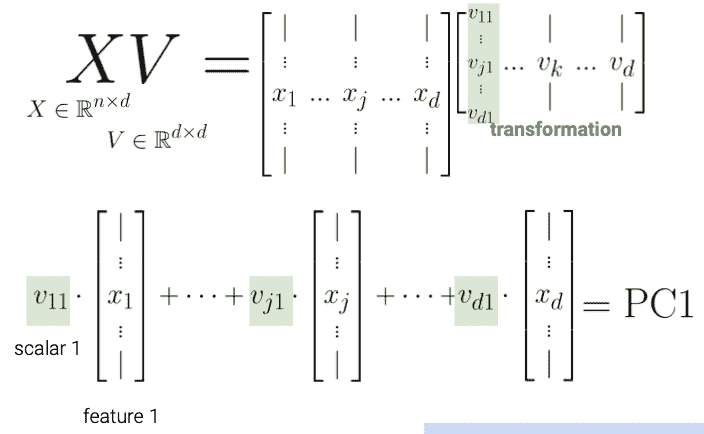UCB Data100:数据科学的原理和技巧:第二十一章到第二十六章
二十一、SQL II
原文:SQL II
译者:飞龙
协议:CC BY-NC-SA 4.0
学习成果
-
介绍过滤组的能力
-
在 SQL 中执行数据清理和文本操作
-
跨表连接数据
在本讲座中,我们将继续上次的工作,介绍一些高级的 SQL 语法。
首先,让我们加载上一堂课的数据库。
# Load the SQL Alchemy Python library
import sqlalchemy
import pandas as pd
%load_ext sql
%%sql
sqlite:///data/basic_examples.db
21.1 过滤组
HAVING通过在每个组的所有行上应用一些条件来过滤组。我们将其解释为只保留具有某些条件的组的一种方式。请注意WHERE和HAVING之间的区别:我们使用WHERE来过滤行,而我们使用HAVING来过滤组。在 SQL 执行查询时,WHERE在HAVING之前。
让我们看看Dish表,看看我们如何使用HAVING。
%%sql
SELECT *
FROM Dish;
* sqlite:///data/basic_examples.db
Done.
| Name | type | cost |
|---|---|---|
| ravioli | entree | 10 |
| ramen | entree | 13 |
| taco | entree | 7 |
| edamame | appetizer | 4 |
| fries | appetizer | 4 |
| potsticker | appetizer | 4 |
| ice cream | dessert | 5 |
下面的代码按类型对不同的菜品进行分组,并仅保留那些最大费用仍然小于 8 的组。
%%sql
SELECT type, COUNT(*)
FROM Dish
GROUP BY type
HAVING MAX(cost) < 8;
* sqlite:///data/basic_examples.db
Done.
| type | COUNT(*) |
|---|---|
| appetizer | 3 |
| dessert | 1 |
相比之下,下面的代码首先过滤成本小于 8 的行,然后进行分组。请注意输出的差异 - 在这种情况下,“taco”也被包括在内,而同一组中其他成本大于或等于 8 的条目则不被包括在内。
%%sql
SELECT type, COUNT(*)
FROM Dish
WHERE cost < 8
GROUP BY type;
* sqlite:///data/basic_examples.db
Done.
| type | COUNT(*) |
|---|---|
| appetizer | 3 |
| dessert | 1 |
| entree | 1 |
21.2 SQL 中的探索性数据分析
在上一堂课中,我们大多是在假设我们的数据已经被清理过的情况下工作。然而,正如我们在数据科学生命周期的第一遍中看到的那样,我们很少会得到没有格式问题的数据。考虑到这一点,我们将学习如何在 SQL 中清理和转换数据。
我们在处理“大数据”时的典型工作流程是:
-
使用 SQL 查询数据库中的数据
-
使用
python(带有pandas)详细分析这些数据
然而,我们仍然可以直接使用 SQL 执行简单的数据清理和重组。为此,我们将使用imdbmini数据库中的Title表。
21.2.1 使用LIKE匹配文本
我们在首次进行探索性数据分析时遇到的一个常见任务是需要匹配字符串数据。例如,我们可能希望在数据清理过程中删除以相同前缀开头的条目。
在 SQL 中,我们使用LIKE运算符来(你猜对了)查找与给定字符串模式相似的字符串。
%%sql
sqlite:///data/imdbmini.db
%%sql
SELECT titleType, primaryTitle
FROM Title
WHERE primaryTitle LIKE "Star Wars: Episode I - The Phantom Menace"
sqlite:///data/basic_examples.db
* sqlite:///data/imdbmini.db
Done.
| titleType | primaryTitle |
|---|---|
| movie | Star Wars: Episode I - The Phantom Menace |
如果我们想要找到所有星球大战电影呢?%是通配符运算符,它表示“查找任意字符,任意次数”。这使得它有助于识别与我们期望提取的模式相似的字符串,即使我们不知道我们的目标模式的完整文本是什么。相比之下,_表示“查找正好 1 个字符”,正如你在随后的哈利波特示例中所看到的。
%%sql
SELECT titleType, primaryTitle
FROM Title
WHERE primaryTitle LIKE "%Star Wars%"
LIMIT 10;
sqlite:///data/basic_examples.db
* sqlite:///data/imdbmini.db
Done.
| titleType | primaryTitle |
|---|---|
| movie | Star Wars: Episode IV - A New Hope |
| movie | Star Wars: Episode V - The Empire Strikes Back |
| movie | Star Wars: Episode VI - Return of the Jedi |
| movie | Star Wars: Episode I - The Phantom Menace |
| movie | Star Wars: Episode II - Attack of the Clones |
| movie | Star Wars: Episode III - Revenge of the Sith |
| tvSeries | Star Wars: Clone Wars |
| tvSeries | Star Wars: The Clone Wars |
| movie | Star Wars: The Clone Wars |
| movie | Star Wars: Episode VII - The Force Awakens |
%%sql
SELECT titleType, primaryTitle
FROM Title
WHERE primaryTitle LIKE "Harry Potter and the Deathly Hallows: Part _"
sqlite:///data/basic_examples.db
* sqlite:///data/imdbmini.db
Done.
| titleType | primaryTitle |
|---|---|
| movie | Harry Potter and the Deathly Hallows: Part 1 |
| movie | Harry Potter and the Deathly Hallows: Part 2 |
21.2.2 数据类型转换
一个常见的数据清理任务是将数据转换为正确的变量类型。CAST关键字用于生成新的输出列。此输出列中的每个条目都是将现有列中的数据转换为新数据类型的结果。例如,我们可能希望将存储为字符串的数字数据转换为整数。
%%sql
SELECT primaryTitle, CAST(runtimeMinutes AS INT), CAST(startYear AS INT)
FROM Title
LIMIT 5
sqlite:///data/basic_examples.db
* sqlite:///data/imdbmini.db
Done.
| primaryTitle | CAST(runtimeMinutes AS INT) | CAST(startYear AS INT) |
|---|---|---|
| A Trip to the Moon | 13 | 1902 |
| The Birth of a Nation | 195 | 1915 |
| The Cabinet of Dr. Caligari | 76 | 1920 |
| The Kid | 68 | 1921 |
| Nosferatu | 94 | 1922 |
我们在为输出表SELECT列时使用CAST。在上面的例子中,我们希望SELECT由CAST创建的整数年份和运行时间数据的列。
SQL 将根据用于SELECT它的命令自动命名一个新列,这可能导致笨拙的列名。我们可以使用AS关键字重命名CAST列。
%%sql
SELECT primaryTitle AS title, CAST(runtimeMinutes AS INT) AS minutes, CAST(startYear AS INT) AS year
FROM Title
LIMIT 5;
sqlite:///data/basic_examples.db
* sqlite:///data/imdbmini.db
Done.
| Title | Minute | Year |
|---|---|---|
| A Trip to the Moon | 13 | 1902 |
| The Birth of a Nation | 195 | 1915 |
| The Cabinet of Dr. Caligari | 76 | 1920 |
| The Kid | 68 | 1921 |
| Nosferatu | 94 | 1922 |
21.2.3 使用CASE的条件语句
在使用pandas时,我们经常遇到希望使用某种形式的条件语句生成新列的情况。例如,假设我们想根据其发行年份将电影标题描述为“老”、“中年”或“新”。
在 SQL 中,使用CASE子句执行条件操作。在概念上,CASE的行为很像CAST操作:它创建一个新列,然后我们可以SELECT它以出现在输出中。CASE子句的语法如下:
CASE WHEN <condition> THEN <value>
WHEN <other condition> THEN <other value>
...
ELSE <yet another value>
END
通过扫描上面的骨架代码,您可以看到逻辑与python中的if语句类似。条件语句首先通过调用CASE打开。每个新条件由WHEN指定,THEN指示满足条件时应填充的值。ELSE指定如果没有满足其他条件应填充的值。最后,END指示条件语句的结束;一旦调用了END,SQL 将继续像往常一样评估查询。
让我们看看这个例子。在下面的例子中,我们给CASE语句创建的新列命名为movie_age。
%%sql
/* If a movie was filmed before 1950, it is "old"
Otherwise, if a movie was filmed before 2000, it is "mid-aged"
Else, a movie is "new" */
SELECT titleType, startYear,
CASE WHEN startYear < 1950 THEN "old"
WHEN startYear < 2000 THEN "mid-aged"
ELSE "new"
END AS movie_age
FROM Title
LIMIT 10;
sqlite:///data/basic_examples.db
* sqlite:///data/imdbmini.db
Done.
| titleType | startYear | movie_age |
|---|---|---|
| short | 1902 | old |
| movie | 1915 | old |
| movie | 1920 | old |
| movie | 1921 | old |
| movie | 1922 | old |
| movie | 1924 | old |
| movie | 1925 | old |
| movie | 1925 | old |
| movie | 1927 | old |
| movie | 1926 | old |
21.3 JOIN表
到目前为止,我们已经熟练地使用 SQL 作为清理、操作和转换表中数据的工具。请注意,这句话特指一个表。如果我们需要的数据分布在多个表中会发生什么?这是在使用 SQL 时需要考虑的重要问题——回想一下,我们最初将 SQL 介绍为一种从数据库查询的语言。数据库通常以多维结构存储数据。换句话说,信息存储在多个表中,每个表包含数据库存储的所有数据的一个小子集。
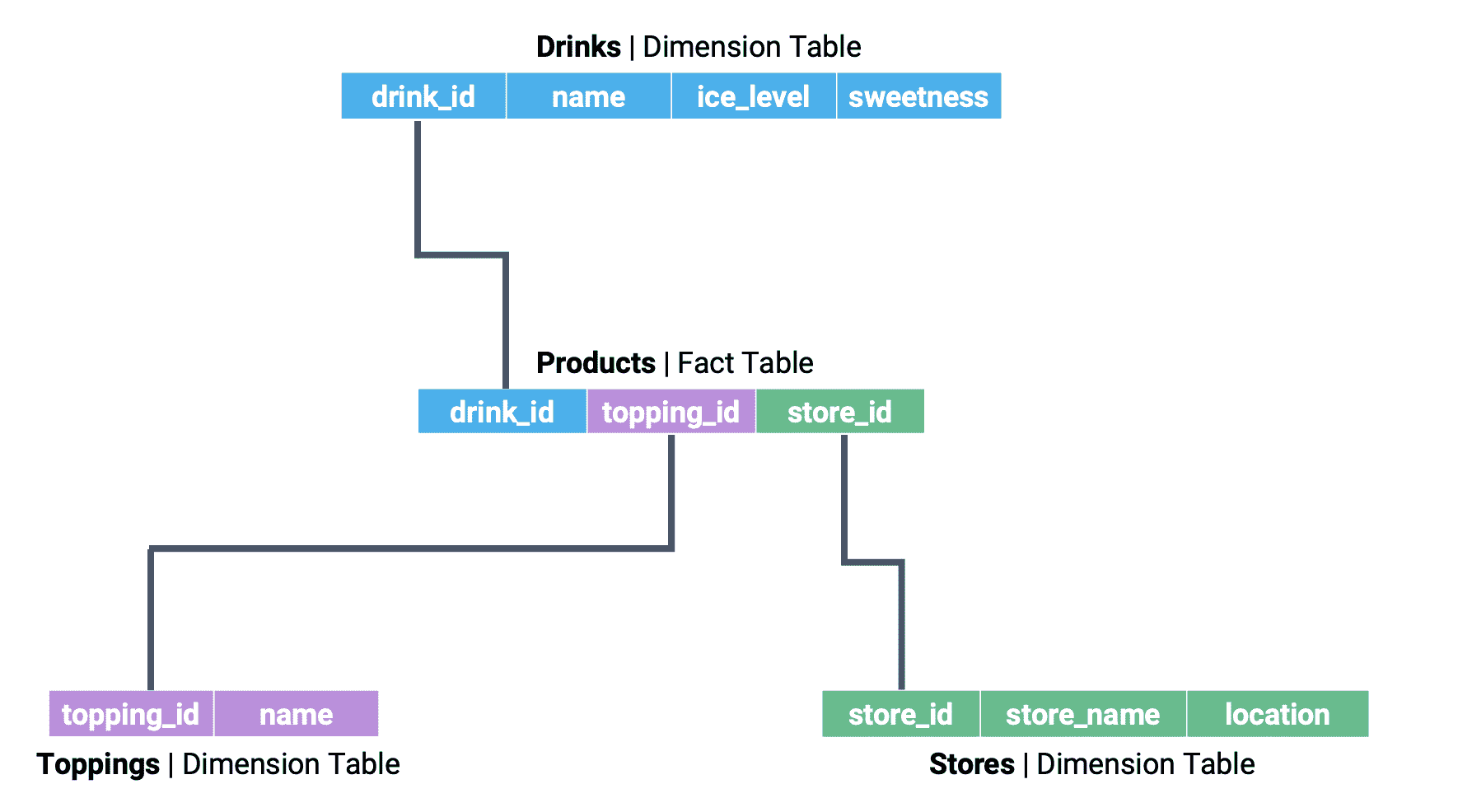
组织数据库的一种常见方式是使用星型模式。星型模式由两种类型的表组成。事实表是数据库的中心表,它包含了跨多个维度表的条目链接所需的信息,维度表包含有关数据的更详细的信息。
假设我们正在处理一个关于伯克利波霸供应的数据库。数据库的维度表可能包含有关茶品种和波霸配料的信息。事实表将用于在各种维度表之间链接这些信息。
如果我们明确标记表之间的关系,我们开始看到星型模式的结构。
要跨多个表连接数据,我们将使用(创造性地命名的)JOIN关键字。我们首先考虑更简单的cats数据集,其中包含表s和t。
要执行连接,我们修改FROM子句。您可以将其视为说:“SELECT我的数据FROM已连接在一起的表。”
记住:SQL 在解释查询时不考虑换行或空格。下面示例中给出的缩进是为了帮助提高可读性。如果愿意,可以编写不遵循此格式的代码。
SELECT <column list>
FROM table_1
JOIN table_2
ON key_1 = key_2;
我们还需要指定应从每个表中使用哪个列来确定匹配的条目。通过定义这些键,我们为 SQL 提供了它需要的信息,以便将数据行配对在一起。
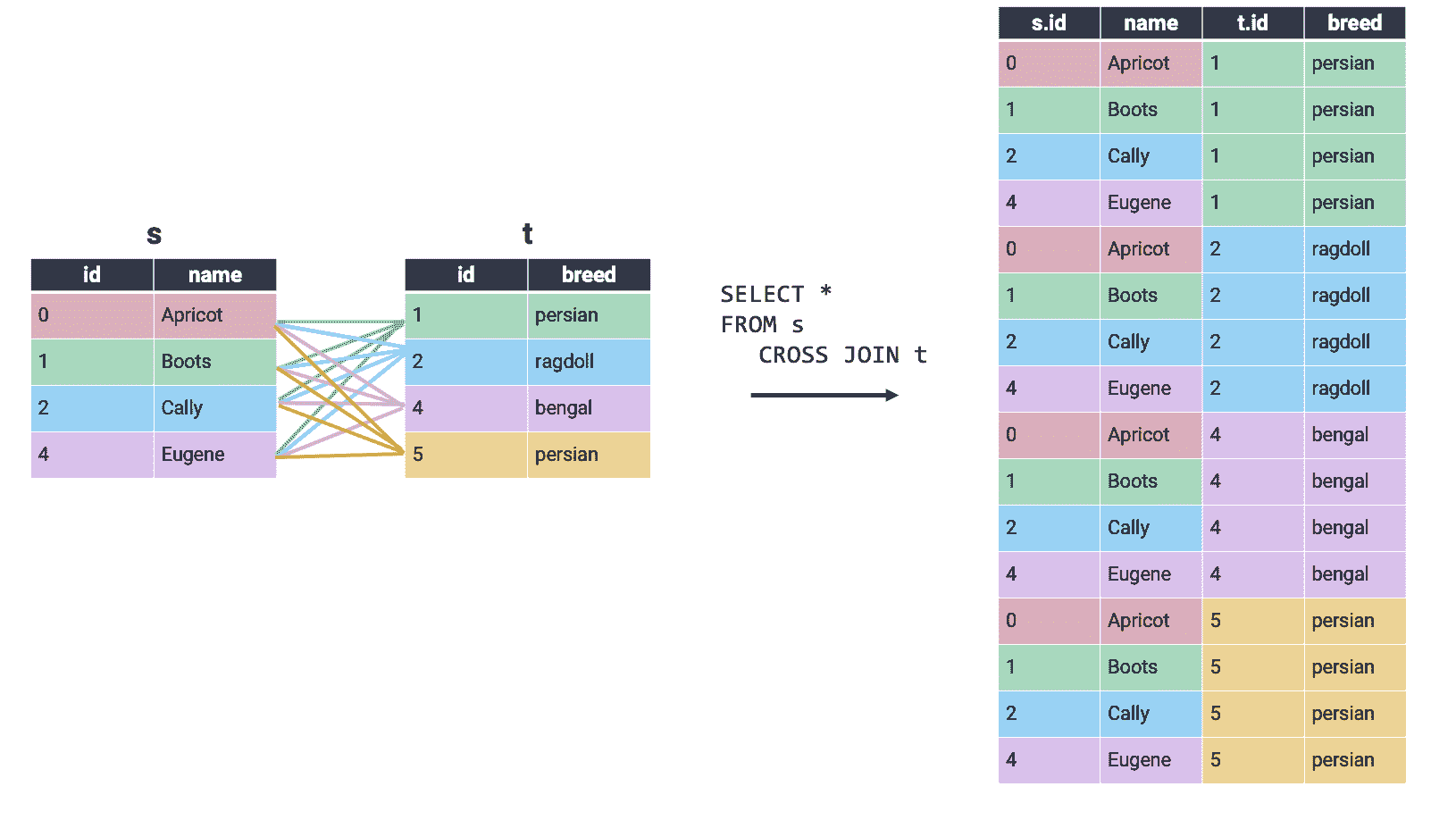
在交叉连接中,输出表中出现所有可能的行组合,无论行是否共享匹配键。因为所有行都被连接,即使没有匹配键,也不需要在ON语句中指定要考虑的键。交叉连接也称为笛卡尔积。
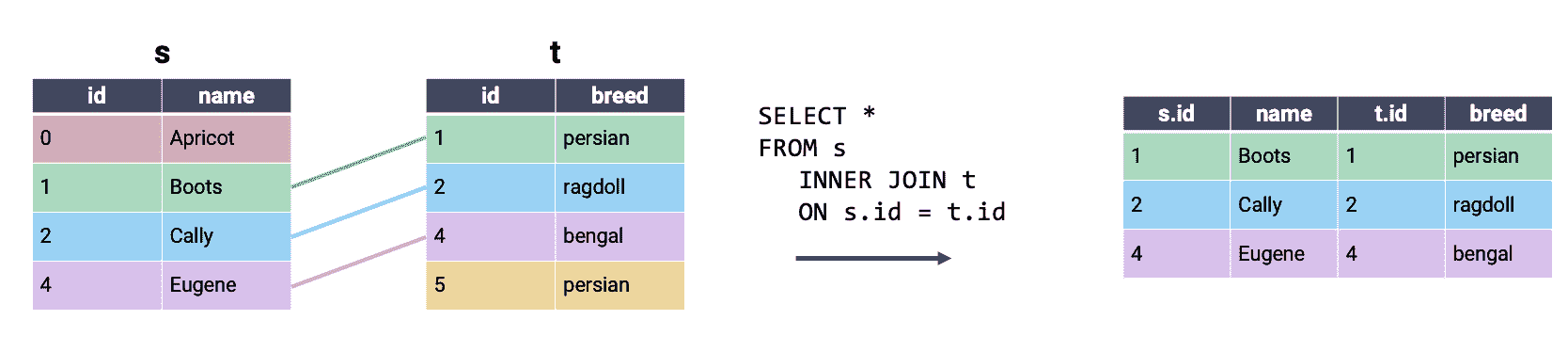
最常用的 SQL JOIN类型是内连接。原来你已经熟悉内连接的作用和工作原理 - 这就是我们一直在pandas中使用的连接类型!在内连接中,我们将第一个表中的每一行与第二个表中的匹配条目组合在一起。如果任一表中的行在另一表中没有匹配项,则将其从输出中省略。
解释内连接的另一种方法:执行交叉连接,然后删除所有不共享匹配键的行。请注意,上面内连接的输出包含交叉连接示例的所有行,该示例在整个行中包含单个颜色。
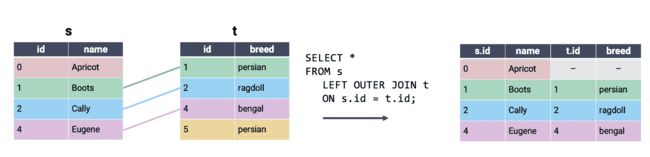
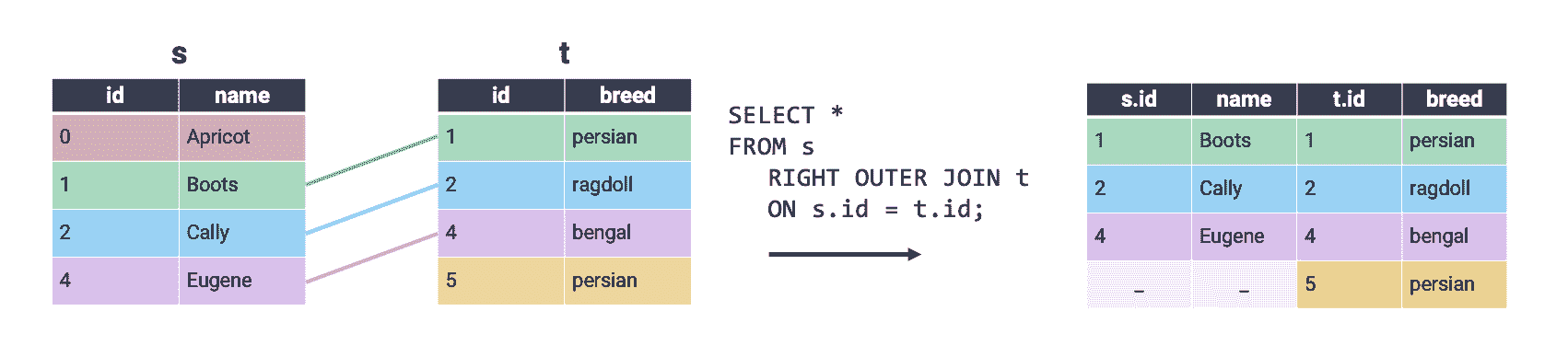
在全外连接中,将两个表之间有匹配的所有行连接在一起。如果一行在第二个表中没有匹配项,则该第二个表的列的值将填充为 null。换句话说,全外连接执行内连接同时保留在另一表中没有匹配的行。这最好通过可视化理解:
我们已经使用内连接实现了相同的输出,同时为在第二个表中没有匹配的S和t条目添加了部分空行。请注意,SQLite 不支持FULL OUTER JOIN,这是实验和作业中将使用的 SQL“风格”。
左外连接类似于全外连接。在左外连接中,输出表中保留了左表中的所有行。如果右表中的行与左表共享匹配,则将保留此行;否则,右表中的行将从输出中省略。
右外连接保留右表中的所有行。只有左表中的行在右表中有匹配时才会保留。SQLite 不支持右外连接。
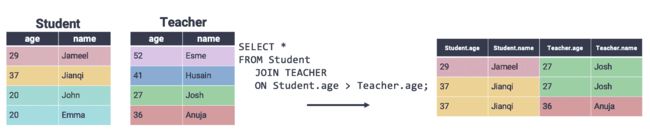
在上面的示例中,我们通过检查两个表之间的相等性(即通过设置s.id = t.id)执行了连接。SQL 还支持在不等式上连接行,这是我们在pandas中无法做到的。考虑一个包含有关学生和教师信息的新数据集。
通常,我们希望比较不同表中行的相对值,而不是检查它们是否完全相等。例如,我们可能希望连接学生比相应的老师年龄大的行。我们可以通过在ON语句中指定不等式来实现这一点。
二十二、逻辑回归 I
原文:Logistic Regression I
译者:飞龙
协议:CC BY-NC-SA 4.0
学习成果
-
了解回归和分类之间的区别
-
推导用于分类数据的逻辑回归模型
-
用交叉熵损失量化我们的逻辑回归模型的错误
到目前为止,在课堂上,我们专注于回归任务 - 也就是说,从给定数据集中预测一个数值数量。我们讨论了优化、特征工程和正则化,都是在执行回归以预测某个数量的情况下。
现在我们对建模任务的可能性有了深入的了解,让我们扩展我们对可能建模任务的了解。
22.1 分类
在接下来的两次讲座中,我们将解决分类的任务。分类问题旨在将数据分类为类别。与回归不同,在回归中我们预测了一个数值输出,分类涉及预测一些分类变量或响应 y y y。分类任务的例子包括:
-
从失误百分比预测哪支球队赢得比赛
-
从总餐厅账单预测一餐的星期几
-
从其马力预测汽车的型号
有几种不同类型的分类:
-
二元分类:将数据分类为两类,响应 y y y要么是 0,要么是 1
-
多类分类:将数据分类为多个类别(例如,图像标记,句子中的下一个单词等)
-
结构化预测任务:进行多个相关的分类预测(例如,翻译,语音识别等)
在 Data 100 中,我们将主要处理二元分类,我们试图将数据分类为两类之一。
为了构建一个分类模型,我们需要稍微修改我们的建模工作流程。回想一下,在回归中我们:
-
创建了一个数值特征的设计矩阵
-
将我们的模型定义为这些数值特征的线性组合
-
使用模型输出数值预测
然而,在分类中,我们不再希望输出数值预测;相反,我们希望预测数据点属于哪个类。这意味着我们需要更新我们的工作流程。为了构建一个分类模型,我们将:
-
创建一个数值特征的设计矩阵。
-
将我们的模型定义为这些数值特征的线性组合,通过非线性sigmoid 函数进行转换。这会输出一个数值数量。
-
应用决策规则来解释输出的数量并决定分类。
-
输出一个预测的类。
有两个关键的区别:正如我们很快会看到的,我们需要加入一个非线性转换来捕捉我们数据中隐藏的非线性关系。我们通过将 sigmoid 函数应用于特征的线性组合来实现这一点。其次,我们必须应用一个决策规则,将我们模型计算出的数值数量转换为实际的类别预测。这可以简单地说,任何具有大于某个数字 x x x的特征的数据点都属于类 1。
这只是一个非常高层次的概述。让我们详细地走一遍流程,澄清我们的意思。
22.2 推导逻辑回归模型
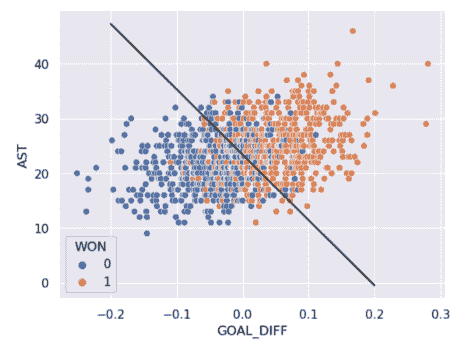
在本讲座中,我们将使用games数据集,其中包含 NBA 篮球联赛中比赛的信息。我们的目标是使用篮球队的GOAL_DIFF来预测给定球队是否赢得比赛(“WON”)。如果一支球队赢得比赛,我们将说他们属于类 1。如果他们输了,他们属于类 0。
对于那些好奇的人,GOAL_DIFF代表两支竞争球队之间成功投篮百分比的差异。
代码
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
np.seterr(divide='ignore')
games = pd.read_csv("data/games").dropna()
games.head()
| GAME_ID | TEAM_NAME | MATCHUP | WON | GOAL_DIFF | AST | |
|---|---|---|---|---|---|---|
| 0 | 21701216 | Dallas Mavericks | DAL vs. PHX | 0 | -0.251 | 20 |
| 1 | 21700846 | Phoenix Suns | PHX @ GSW | 0 | -0.237 | 13 |
| 2 | 21700071 | San Antonio Spurs | SAS @ ORL | 0 | -0.234 | 19 |
| 3 | 21700221 | New York Knicks | NYK @ TOR | 0 | -0.234 | 17 |
| 4 | 21700306 | Miami Heat | MIA @ NYK | 0 | -0.222 | 21 |
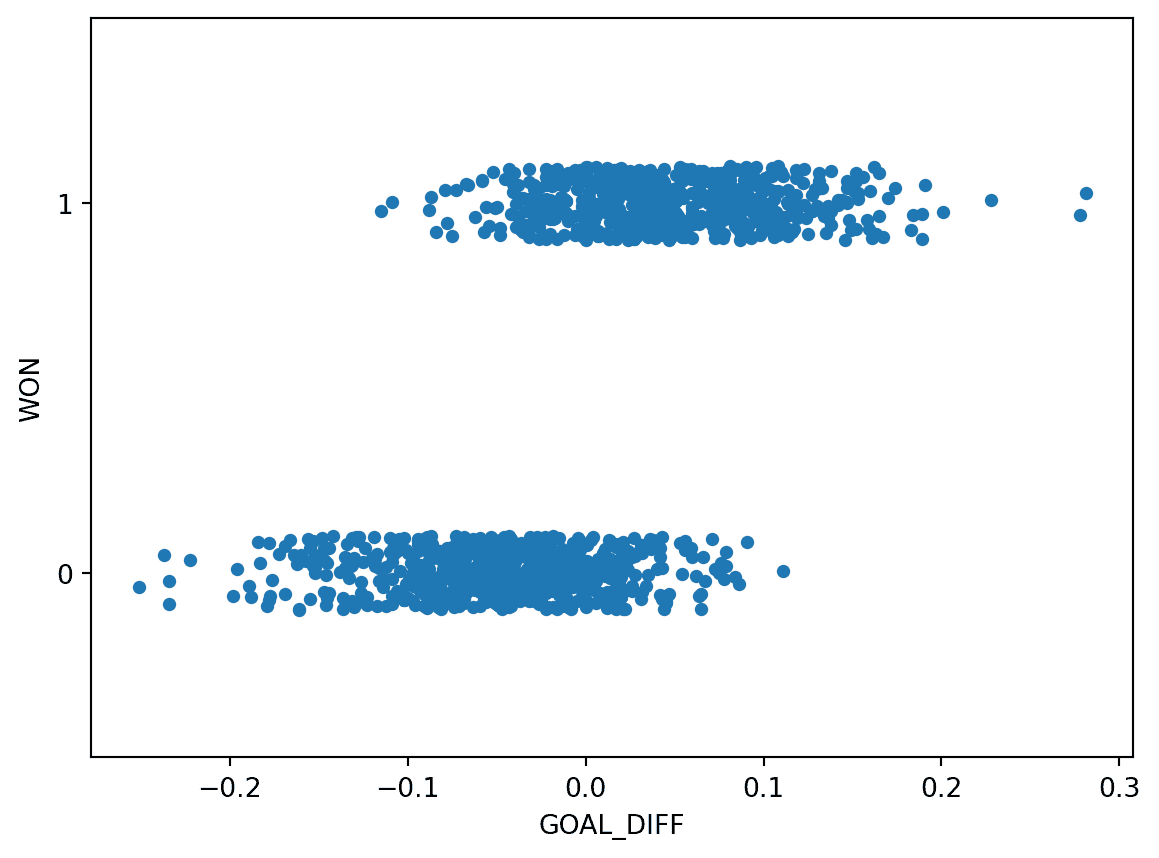
让我们使用 Seaborn 函数sns.stripplot来可视化"GOAL_DIFF"和"WON"之间的关系。条带图会自动引入一小部分随机噪声来使数据发生抖动。回想一下,"WON"列中的所有值都是 1(赢)或 0(输)- 如果我们直接绘制它们而不进行抖动,我们将看到严重的重叠。
Code
import seaborn as sns
import matplotlib.pyplot as plt
sns.stripplot(data=games, x="GOAL_DIFF", y="WON", orient="h")
# By default, sns.stripplot plots 0, then 1\. We invert the y axis to reverse this behavior
plt.gca().invert_yaxis();
这个数据集不像我们以前见过的任何东西-我们的目标变量只包含两个唯一的值!记住,每个 y 值要么是 0,要么是 1;上面的图稍微抖动了 y 数据以便阅读。
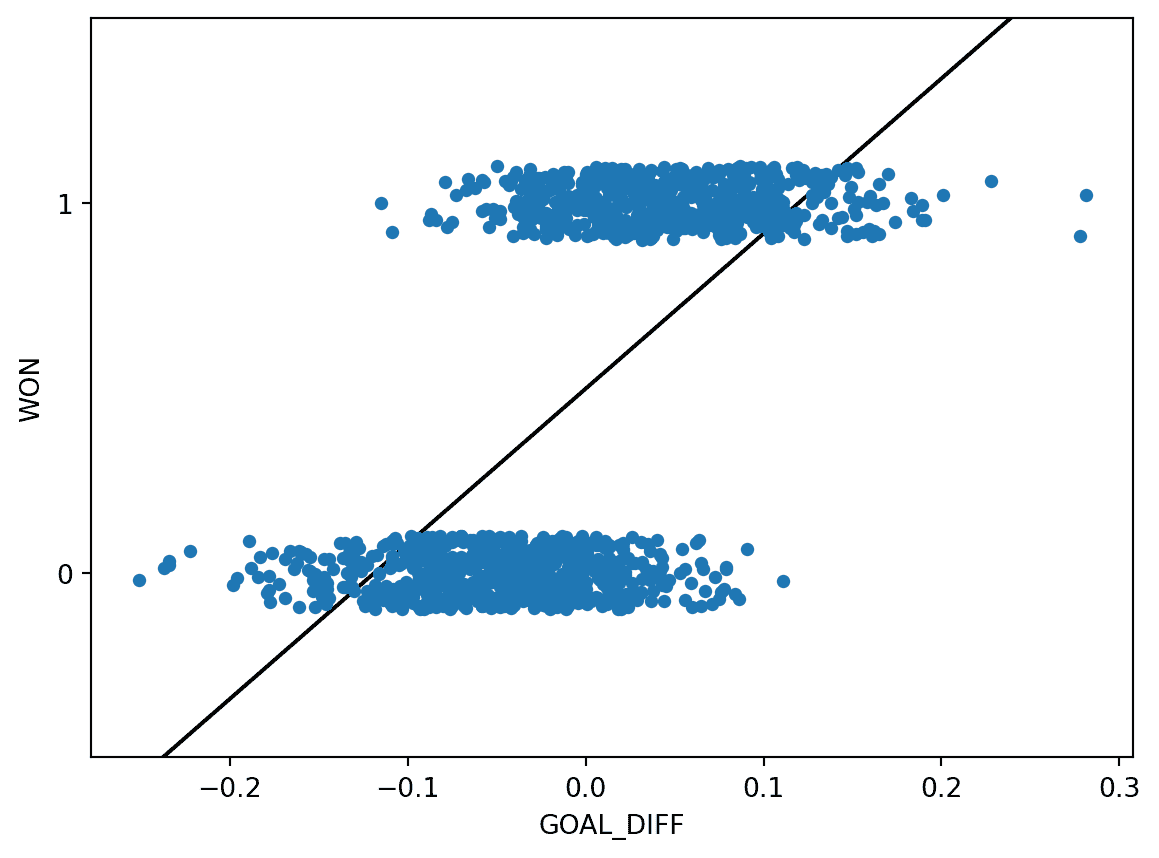
我们所使用的回归模型总是假设我们试图预测一个连续的目标。如果我们将线性回归模型应用于这个数据集,会发生一些奇怪的事情。
Code
import sklearn.linear_model as lm
X, Y = games[["GOAL_DIFF"]], games["WON"]
regression_model = lm.LinearRegression()
regression_model.fit(X, Y)
plt.plot(X.squeeze(), regression_model.predict(X), "k")
sns.stripplot(data=games, x="GOAL_DIFF", y="WON", orient="h")
plt.gca().invert_yaxis();
线性回归拟合尽可能地与数据保持一致。然而,这种方法存在一些关键缺陷:
-
预测输出 y ^ \hat{y} y^可能超出可能类别的范围(有预测值大于 1 和小于 0)
-
这意味着输出并不总是可以解释(预测-2.3 的类别意味着什么?)
我们通常的线性回归框架在这里行不通。相反,我们需要更有创意。
回到Data 8,你通过使用平均值图逐渐建立了线性回归的概念。在你了解回归线的数学基础之前,你采取了更直观的方法:将 x x x数据分成常见值的箱子,然后计算相同箱子中所有数据点的平均 y y y。结果为你提供了推导回归拟合所需的洞察力。
让我们采用与我们应对新的分类任务相同的方法。在下面的单元格中,我们 1)将"GOAL_DIFF"数据分成相似值的箱子,2)计算箱子中所有数据点的平均"WON"值。
bins = pd.cut(games["GOAL_DIFF"], 20)
games["bin"] = [(b.left + b.right) / 2 for b in bins]
win_rates_by_bin = games.groupby("bin")["WON"].mean()
# alpha makes the points transparent so we can see the line more clearly
sns.stripplot(data=games, x="GOAL_DIFF", y="WON", orient="h", alpha=0.3)
plt.plot(win_rates_by_bin.index, win_rates_by_bin, c="tab:red")
plt.gca().invert_yaxis();
有趣的是:我们的结果肯定不像通过找到线性关系的平均值图产生的直线。我们可以做两个观察:
-
我们线上的所有预测都在 0 和 1 之间
-
预测是非线性的,遵循一个粗略的“S”形状
让我们更深入地思考一下我们刚刚做的事情。
为了找到每个箱子的平均 y y y值,我们计算:
1 (# Y = 1 in bin) + 0 (# Y = 0 in bin) # datapoints in bin = # Y = 1 in bin # datapoints in bin = P ( Y = 1 ∣ bin ) \frac{1 \text{(\# Y = 1 in bin)} + 0 \text{(\# Y = 0 in bin)}}{\text{\# datapoints in bin}} = \frac{\text{\# Y = 1 in bin}}{\text{\# datapoints in bin}} = P(\text{Y = 1} | \text{bin}) # datapoints in bin1(# Y = 1 in bin)+0(# Y = 0 in bin)=# datapoints in bin# Y = 1 in bin=P(Y = 1∣bin)
这只是该箱中数据点属于类别 1 的概率!这与我们之前的观察一致:我们所有的预测都在 0 和 1 之间,正如我们对概率的预期一样。
我们的平均值图实际上在建模概率 p p p,即数据点属于类别 1 的概率,或者本质上是对于特定值的 x \text{x} x, Y = 1 \text{Y = 1} Y = 1的概率。
p = P ( Y = 1 ∣ x ) p = P(Y = 1 | \text{ x} ) p=P(Y=1∣ x)
在逻辑回归中,我们有一个新的建模目标。我们想要建模特定数据点属于类别 1 的概率。为此,我们需要创建一个可以近似我们上面绘制的 S 形曲线的模型。
对我们来说幸运的是,我们已经熟悉了一种模拟非线性关系的技术——对线性关系进行非线性转换。回想一下我们之前应用过的步骤:
-
对变量进行转换,直到线性化它们的关系
-
对转换后的变量拟合线性模型
-
“撤销”我们的转换,以确定原始变量之间的基本关系
在过去的例子中,我们使用了凸起图来帮助我们决定哪些转换可能有用。然而,我们上面看到的 S 形曲线与我们过去看到的任何关系都不相似。我们需要仔细考虑哪些转换会线性化这条曲线。
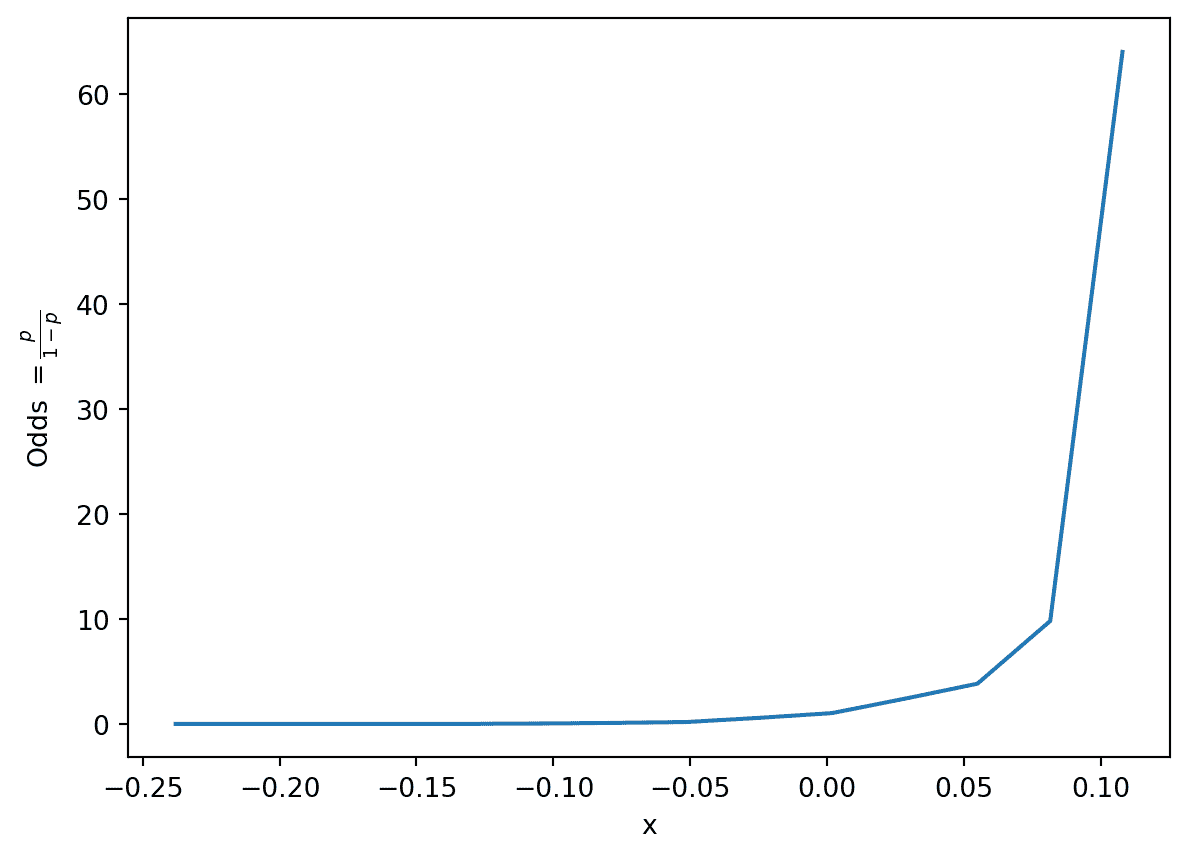
让我们考虑我们最终的目标:确定我们是否应该预测每个数据点的类别是 0 还是 1。换句话说,我们想要确定数据点更“可能”属于类别 0 还是类别 1。决定这一点的一种方法是看哪个类别对于给定的数据点有更高的预测概率。赔率被定义为数据点属于类别 1 的概率除以它属于类别 0 的概率。
odds = P ( Y = 1 ∣ x ) P ( Y = 0 ∣ x ) = p 1 − p \text{odds} = \frac{P(Y=1|x)}{P(Y=0|x)} = \frac{p}{1-p} odds=P(Y=0∣x)P(Y=1∣x)=1−pp
如果我们为每个输入GOAL_DIFF( x x x)绘制赔率,我们会看到一些看起来更有希望的东西。
p = win_rates_by_bin
odds = p/(1-p)
plt.plot(odds.index, odds)
plt.xlabel("x")
plt.ylabel(r"Odds $= \frac{p}{1-p}$");
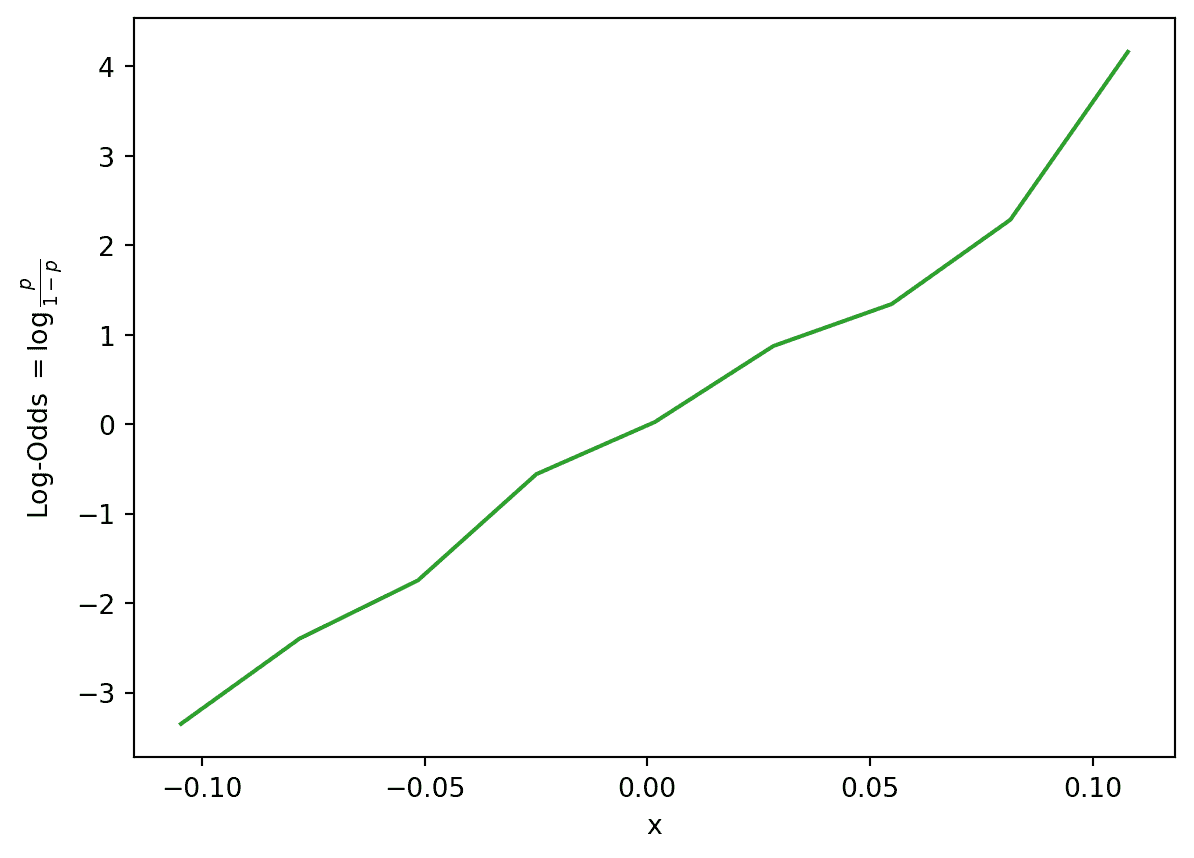
事实证明,我们的输入GOAL_DIFF和赔率之间的关系大致是指数的!让我们通过取对数来线性化指数。作为提醒,你应该假设 Data 100 中的任何对数都是以 e e e为底的自然对数,除非另有说明。
import numpy as np
log_odds = np.log(odds)
plt.plot(odds.index, log_odds, c="tab:green")
plt.xlabel("x")
plt.ylabel(r"Log-Odds $= \log{\frac{p}{1-p}}$");
我们看到了一些有希望的东西——对数几率和我们的输入特征之间的关系大致是线性的。这意味着我们可以使用线性模型来描述对数几率和 x x x之间的关系。换句话说:
log ( p 1 − p ) = θ 0 + θ 1 x i = x ⊤ θ \begin{align} \log{(\frac{p}{1-p})} &= \theta_0 + \theta_1 x_i\\ &= x^{\top} \theta \end{align} log(1−pp)=θ0+θ1xi=x⊤θ
在这里,我们使用 x ⊤ x^{\top} x⊤来表示数据集中的一个观察值,存储为行向量。你可以想象它是我们设计矩阵中的一行。 x ⊤ θ x^{\top} \theta x⊤θ表示这个观察的特征的线性组合(就像我们在多元线性回归中使用的那样)。
我们做得很好!我们现在得出了以下关系:
log ( p 1 − p ) = x ⊤ θ \log{(\frac{p}{1-p})} = x^{\top} \theta log(1−pp)=x⊤θ
记住我们的目标是预测数据点属于类别 1 的概率 p p p。让我们重新排列这个关系,以揭示 p p p和我们的输入数据 x ⊤ x^{\top} x⊤之间的原始关系。
log ( p 1 − p ) = x T θ p 1 − p = e x T θ p = ( 1 − p ) e x T θ p = e x T θ − p e x T θ p ( 1 + e x T θ ) = e x T θ p = e x T θ 1 + e x T θ p = 1 1 + e − x T θ \begin{align} \log{(\frac{p}{1-p})} &= x^T \theta\\ \frac{p}{1-p} &= e^{x^T \theta}\\ p &= (1-p)e^{x^T \theta}\\ p &= e^{x^T \theta}- p e^{x^T \theta}\\ p(1 + e^{x^T \theta}) &= e^{x^T \theta} \\ p &= \frac{e^{x^T \theta}}{1+e^{x^T \theta}}\\ p &= \frac{1}{1+e^{-x^T \theta}}\\ \end{align} log(1−pp)1−ppppp(1+exTθ)pp=xTθ=exTθ=(1−p)exTθ=exTθ−pexTθ=exTθ=1+exTθexTθ=1+e−xTθ1
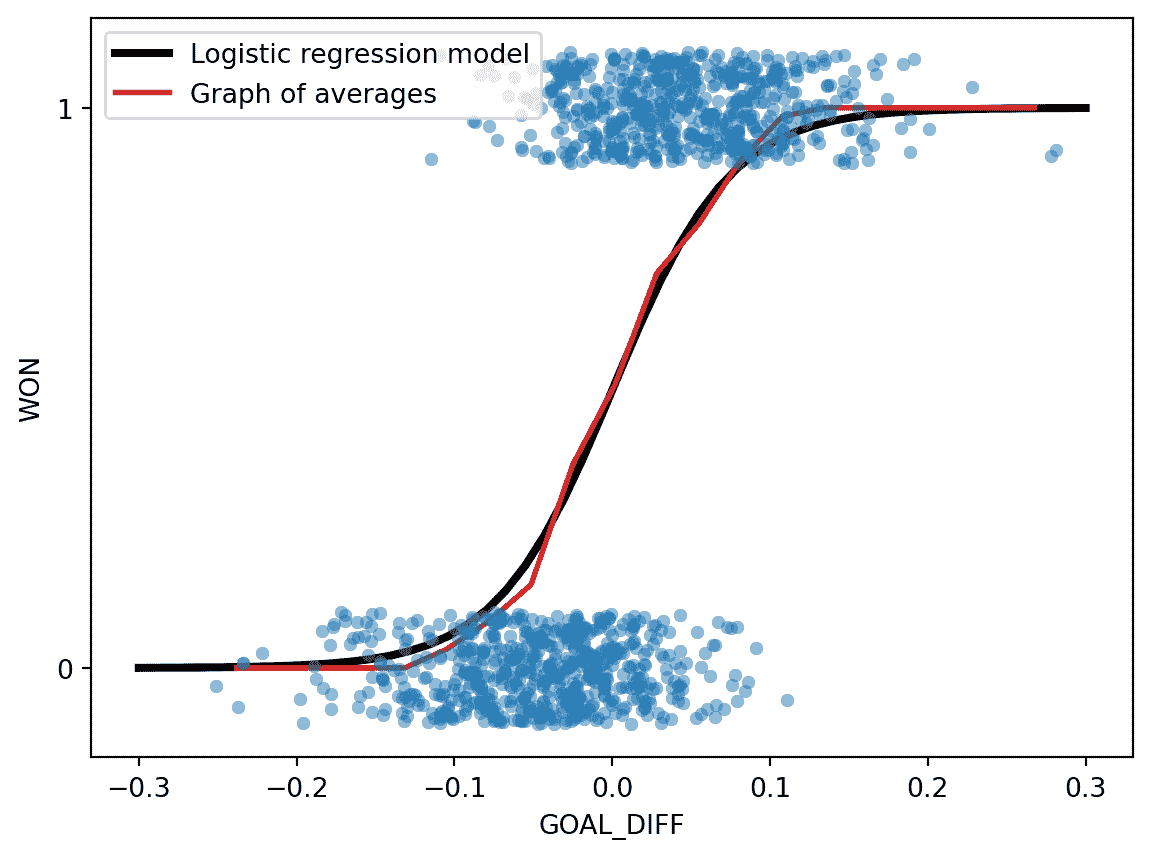
哎呀,这是很多代数。我们发现的是用于预测数据点 x ⊤ x^{\top} x⊤属于类别 1 的逻辑回归模型。如果我们为我们的数据绘制这种关系,我们会看到之前的 S 形曲线!
代码
# We'll discuss the `LogisticRegression` class next time
xs = np.linspace(-0.3, 0.3)
logistic_model = lm.LogisticRegression(C=20)
logistic_model.fit(X, Y)
predicted_prob = logistic_model.predict_proba(xs[:, np.newaxis])[:, 1]
sns.stripplot(data=games, x="GOAL_DIFF", y="WON", orient="h", alpha=0.5)
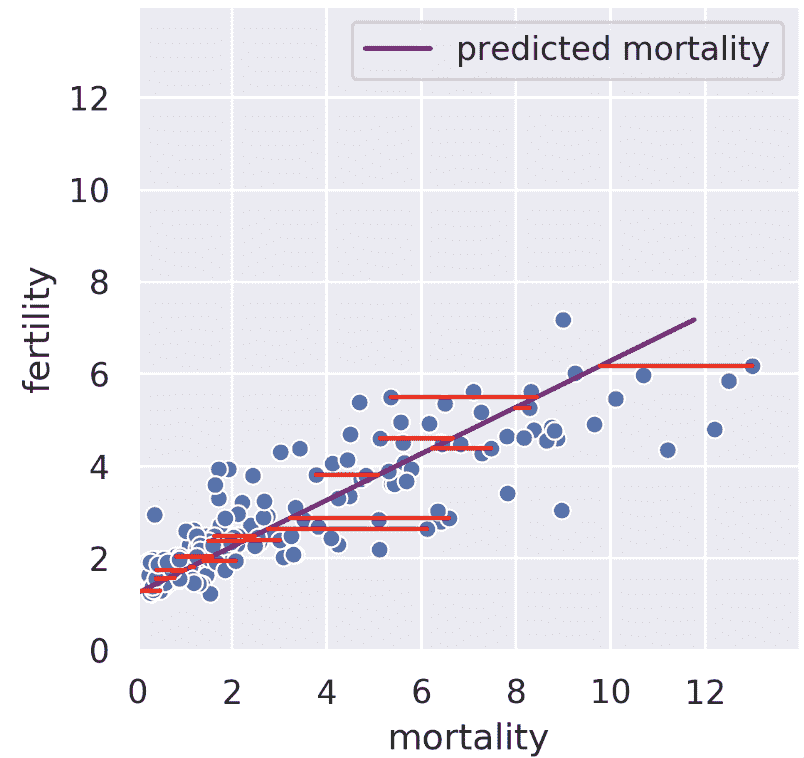
plt.plot(xs, predicted_prob, c="k", lw=3, label="Logistic regression model")
plt.plot(win_rates_by_bin.index, win_rates_by_bin, lw=2, c="tab:red", label="Graph of averages")
plt.legend(loc="upper left")
plt.gca().invert_yaxis();
使用逻辑回归模型来预测概率时,我们:
-
计算特征的线性组合 x ⊤ θ x^{\top}\theta x⊤θ
-
应用 Sigmoid 激活函数, σ ( x ⊤ θ ) \sigma(x^{\top} \theta) σ(x⊤θ)。
我们的预测概率的形式为 P ( Y = 1 ∣ x ) = p = 1 1 + e − ( θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ p x p ) P(Y=1|x) = p = \frac{1}{1+e^{-(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_p x_p)}} P(Y=1∣x)=p=1+e−(θ0+θ1x1+θ2x2+…+θpxp)1
重要说明:尽管名字是这样,逻辑回归用于分类任务,而不是回归任务。在 Data 100 中,我们总是应用逻辑回归来分类数据。
S 形曲线在正式上被称为Sigmoid 函数,通常用 σ \sigma σ表示。
σ ( t ) = 1 1 + e − t \sigma(t) = \frac{1}{1+e^{-t}} σ(t)=1+e−t1
Sigmoid 的属性
-
反射/对称: 1 − σ ( t ) = e − t 1 + e − t = σ ( − t ) 1-\sigma(t) = \frac{e^{-t}}{1+e^{-t}}=\sigma(-t) 1−σ(t)=1+e−te−t=σ(−t)
-
反函数: t = σ − 1 ( p ) = log ( p 1 − p ) t=\sigma^{-1}(p)=\log{(\frac{p}{1-p})} t=σ−1(p)=log(1−pp)
-
导数: d d z σ ( t ) = σ ( t ) ( 1 − σ ( t ) ) = σ ( t ) σ ( − t ) \frac{d}{dz} \sigma(t) = \sigma(t) (1-\sigma(t))=\sigma(t)\sigma(-t) dzdσ(t)=σ(t)(1−σ(t))=σ(t)σ(−t)
-
域: − ∞ < t < ∞ -\infty < t < \infty −∞<t<∞
-
范围: 0 < σ ( t ) < 1 0 < \sigma(t) < 1 0<σ(t)<1
在我们建模过程的背景下,Sigmoid 被认为是一个激活函数。它接收特征的线性组合并应用非线性变换。
让我们总结一下我们的逻辑回归建模工作流程。
我们从本节中得出的主要结论是:
-
尽量最好地拟合“S”曲线
-
曲线模拟了概率: P = ( Y = 1 ∣ x ) P = (Y=1 | x) P=(Y=1∣x)
-
假设对数几率是 x x x和 θ \theta θ的线性组合
综上所述,我们知道给定特征 x x x的响应的估计概率等于在值 x ⊤ θ x^{\top}\theta x⊤θ处的逻辑函数 σ ( ) \sigma() σ():
P ^ θ ( Y = 1 ∣ x ) = 1 1 + e − x ⊤ θ \begin{align} \hat{P}_{\theta}(Y = 1 | x) = \frac{1}{1 + e^{-x^{\top}\theta}} \end{align} P^θ(Y=1∣x)=1+e−x⊤θ1
更常见的是,逻辑回归模型被写成:
P ^ θ ( Y = 1 ∣ x ) = σ ( x ⊤ θ ) \begin{align} \hat{P}_{\theta}(Y = 1 | x) = \sigma(x^{\top}\theta) \end{align} P^θ(Y=1∣x)=σ(x⊤θ)
逻辑模型的属性
考虑一个具有一个特征和一个截距项的逻辑回归模型:
p = P ( Y = 1 ∣ x ) = 1 1 + e − ( θ 0 + θ 1 x ) \begin{align} p = P(Y = 1 | x) = \frac{1}{1+e^{-(\theta_0 + \theta_1 x)}} \end{align} p=P(Y=1∣x)=1+e−(θ0+θ1x)1
属性:
-
θ 0 \theta_0 θ0 控制曲线沿水平轴的位置
-
θ 1 \theta_1 θ1的大小控制了 Sigmoid 的“陡峭度”
-
θ 1 \theta_1 θ1的符号控制曲线的方向
*示例计算
假设我们想要预测一个球队赢得比赛的概率,给定GOAL_DIFF(第一个特征)和罚球次数(第二个特征)。假设我们使用训练数据拟合了一个逻辑回归模型(没有截距),并估计了最优参数。现在我们想要预测一个新球队赢得比赛的概率。
θ ^ ⊤ = [ 0.1 − 0.5 ] x ⊤ = [ 15 1 ] \begin{align} \hat{\theta}^{\top} = \begin{matrix}[0.1 & -0.5]\end{matrix} \\x^{\top} = \begin{matrix}[15 & 1]\end{matrix} \end{align} θ^⊤=[0.1−0.5]x⊤=[151]
P ^ θ ^ ( Y = 1 ∣ x ) = σ ( x ⊤ θ ^ ) = σ ( 0.1 ⋅ 15 + ( − 0.5 ) ⋅ 1 ) = σ ( 1 ) = 1 1 + e − 1 ≈ 0.7311 \begin{align} \hat{P}_{\hat{\theta}}(Y = 1 | x) = \sigma(x^{\top}\hat{\theta}) = \sigma(0.1 \cdot 15 + (-0.5) \cdot 1) = \sigma(1) = \frac{1}{1+e^{-1}} \approx 0.7311 \end{align} P^θ^(Y=1∣x)=σ(x⊤θ^)=σ(0.1⋅15+(−0.5)⋅1)=σ(1)=1+e−11≈0.7311
我们看到响应更可能是 1 而不是 0,这表明一个合理的预测是 y ^ = 1 \hat{y} = 1 y^=1。我们将在下一讲中更深入地讨论这个问题。
22.3 交叉熵损失
为了量化我们的逻辑回归模型的误差,我们需要定义一个损失函数。
22.3.1 为什么不用 MSE?
你可能会想:为什么不使用我们熟悉的均方误差?事实证明,均方误差不适用于逻辑回归。为了理解原因,让我们考虑一个简单的、人工生成的“玩具”数据集(这比更复杂的“游戏”数据更容易处理)。
代码
toy_df = pd.DataFrame({
"x": [-4, -2, -0.5, 1, 3, 5],
"y": [0, 0, 1, 0, 1, 1]})
toy_df.head()
| x | y | |
|---|---|---|
| 0 | -4.0 | 0 |
| 1 | -2.0 | 0 |
| 2 | -0.5 | 1 |
| 3 | 1.0 | 0 |
| 4 | 3.0 | 1 |
我们将构建一个只有一个特征和没有截距项的基本逻辑回归模型。我们的预测概率的形式为:
p = P ( Y = 1 ∣ x ) = 1 1 + e − θ 1 x p=P(Y=1|x)=\frac{1}{1+e^{-\theta_1 x}} p=P(Y=1∣x)=1+e−θ1x1
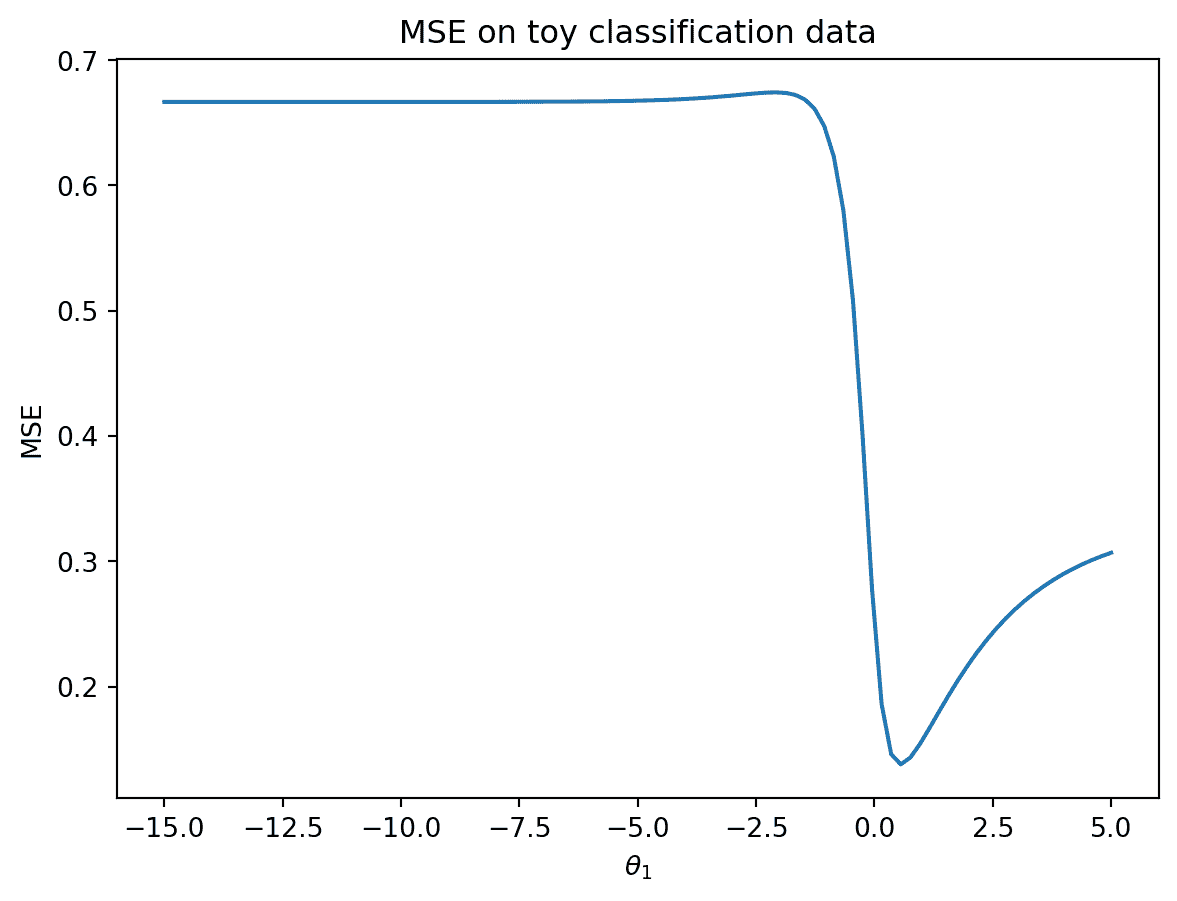
在下面的单元格中,我们绘制了模型在数据上的 MSE。
代码
def sigmoid(z):
return 1/(1+np.e**(-z))
def mse_on_toy_data(theta):
p_hat = sigmoid(toy_df['x'] * theta)
return np.mean((toy_df['y'] - p_hat)**2)
thetas = np.linspace(-15, 5, 100)
plt.plot(thetas, [mse_on_toy_data(theta) for theta in thetas])
plt.title("MSE on toy classification data")
plt.xlabel(r'$\theta_1/details>)
plt.ylabel('MSE');
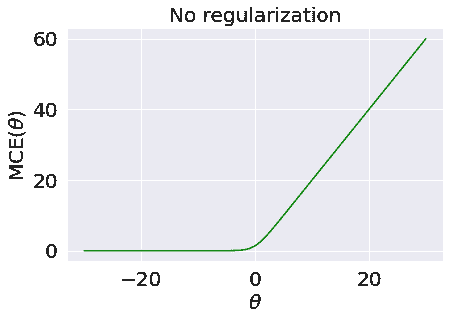
当我们绘制线性回归模型的 MSE 时,这看起来一点也不像我们找到的抛物线!特别是,我们可以确定使用 MSE 进行逻辑回归有两个缺陷:
-
MSE 损失曲面是非凸的。在上面的损失曲面中既有全局最小值,也有一个(几乎不可察觉的)局部最小值。这意味着梯度下降有可能收敛到损失曲面的局部最小值,错过真正的最优参数 θ 1 \theta_1 θ1。
-
对于分类任务,平方损失是有界的。回想一下,每个真实的 y y y 的值要么是 0,要么是 1。这意味着即使我们的模型做出了最糟糕的预测(例如对于 y = 1 y=1 y=1 预测 p = 0 p=0 p=0),一个观察的平方损失也不会大于 1: ( y − p ) 2 = ( 1 − 0 ) 2 = 1 (y-p)^2=(1-0)^2=1 (y−p)2=(1−0)2=1 均方误差并不会严厉地惩罚糟糕的预测。
22.3.2 激励交叉熵损失
可以说,我们不想在逻辑回归中使用均方误差。相反,我们将考虑在损失函数中看到的希望看到的行为。
让 y y y 为二进制标签 0 , 1 {0, 1} 0,1, p p p 是模型预测标签为 1 的概率。
-
当真实的 y y y 为 1 时,当模型预测大的 p p p 时,我们应该承担低的损失
-
当真实的 y y y 为 0 时,当模型预测大的 p p p 时,我们应该承担高的损失
换句话说,我们的损失函数应该根据真实类别 y y y 的值而有所不同。
交叉熵损失包含了这种变化行为。我们将在逻辑回归的工作中使用它。下面,我们写出了单个数据点的交叉熵损失(暂时还没有平均值)。
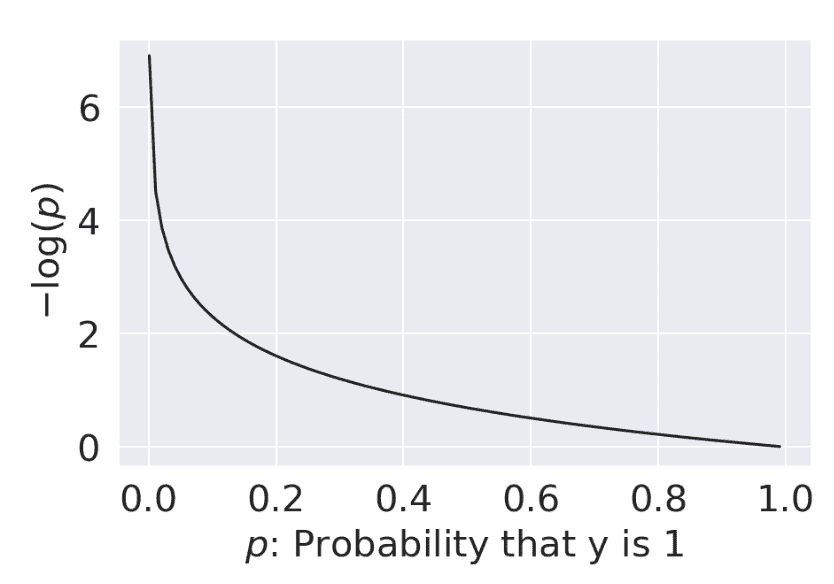
交叉熵损失 = { − log ( p ) if y = 1 − log ( 1 − p ) if y = 0 \text{交叉熵损失} = \begin{cases} -\log{(p)} & \text{if } y=1 \\ -\log{(1-p)} & \text{if } y=0 \end{cases} 交叉熵损失={−log(p)−log(1−p)if y=1if y=0
为什么这种(看似复杂的)损失函数“有效”?让我们来分解一下。
-
当 p → 0 p \rightarrow 0 p→0 时,损失趋近于 ∞ \infty ∞
-
当 p → 1 p \rightarrow 1 p→1 时,损失趋近于 0
-
当 p → 0 p \rightarrow 0 p→0 时,损失趋近于 0
-
当 p → 1 p \rightarrow 1 p→1 时,损失趋近于 ∞ \infty ∞
一切顺利 - 我们看到了我们希望在逻辑回归模型中看到的行为。
我们上面概述的分段函数很难优化:我们不想在选择最佳模型参数的每一步不断“检查”应该使用损失函数的哪种形式。我们可以以更方便的方式重新表达交叉熵损失:
交叉熵损失 = − ( y log ( p ) − ( 1 − y ) log ( 1 − p ) ) \text{交叉熵损失} = -\left(y\log{(p)}-(1-y)\log{(1-p)}\right) 交叉熵损失=−(ylog(p)−(1−y)log(1−p))
通过将 y y y 设置为 0 或 1,我们看到这种新形式的交叉熵损失给了我们与原始公式相同的行为。
当 y = 1 y=1 y=1:
CE = − ( ( 1 ) log ( p ) − ( 1 − 1 ) log ( 1 − p ) ) = − log ( p ) \begin{align} \text{CE} &= -\left((1)\log{(p)}-(1-1)\log{(1-p)}\right)\\ &= -\log{(p)} \end{align} CE=−((1)log(p)−(1−1)log(1−p))=−log(p)
当 y = 0 y=0 y=0:
CE = − ( ( 0 ) log ( p ) − ( 1 − 0 ) log ( 1 − p ) ) = − log ( 1 − p ) \begin{align} \text{CE} &= -\left((0)\log{(p)}-(1-0)\log{(1-p)}\right)\\ &= -\log{(1-p)} \end{align} CE=−((0)log(p)−(1−0)log(1−p))=−log(1−p)
逻辑回归模型的经验风险是数据集中所有数据点的平均交叉熵损失。在拟合模型时,我们希望确定导致最低平均交叉熵损失的模型参数 θ \theta θ。
R ( θ ) = − 1 n ∑ i = 1 n ( y i log ( p i ) − ( 1 − y i ) log ( 1 − p i ) ) R(\theta) = - \frac{1}{n} \sum_{i=1}^n \left(y_i\log{(p_i)}-(1-y_i)\log{(1-p_i)}\right) R(θ)=−n1i=1∑n(yilog(pi)−(1−yi)log(1−pi))
R ( θ ) = − 1 n ∑ i = 1 n ( y i log ( σ ( X i ⊤ θ ) − ( 1 − y i ) log ( 1 − σ ( X i ⊤ θ ) ) R(\theta) = - \frac{1}{n} \sum_{i=1}^n \left(y_i\log{(\sigma(X_i^{\top}\theta)}-(1-y_i)\log{(1-\sigma(X_i^{\top}\theta)}\right) R(θ)=−n1i=1∑n(yilog(σ(Xi⊤θ)−(1−yi)log(1−σ(Xi⊤θ))
因此,优化问题是找到最小化 R ( θ ) R(\theta) R(θ) 的估计 θ ^ \hat{\theta} θ^:
θ ^ = arg min θ = − 1 n ∑ i = 1 n ( y i log ( σ ( X i ⊤ θ ) − ( 1 − y i ) log ( 1 − σ ( X i ⊤ θ ) ) \begin{align} \hat{\theta} = \underset{\theta}{\arg\min} = - \frac{1}{n} \sum_{i=1}^n \left(y_i\log{(\sigma(X_i^{\top}\theta)}-(1-y_i)\log{(1-\sigma(X_i^{\top}\theta)}\right) \end{align} θ^=θargmin=−n1i=1∑n(yilog(σ(Xi⊤θ)−(1−yi)log(1−σ(Xi⊤θ))
绘制我们的toy数据集的交叉熵损失曲面给了我们一个更令人鼓舞的结果 - 我们的损失函数现在是凸的。这意味着我们可以使用梯度下降来优化它。计算逻辑模型的梯度是相当具有挑战性的,所以我们会让sklearn来为我们处理这个问题。在 Data 100 中,您不需要计算逻辑模型的梯度。
代码
def cross_entropy(y, p_hat):
return - y * np.log(p_hat) - (1 - y) * np.log(1 - p_hat)
def mean_cross_entropy_on_toy_data(theta):
p_hat = sigmoid(toy_df['x'] * theta)
return np.mean(cross_entropy(toy_df['y'], p_hat))
plt.plot(thetas, [mean_cross_entropy_on_toy_data(theta) for theta in thetas], color = 'green')
plt.ylabel(r'Mean Cross-Entropy Loss($\theta$)')
plt.xlabel(r'$\theta/details>);
22.4 (奖励) 最大似然估计
看起来我们是凭空提出了交叉熵损失。我们怎么知道取负对数的概率会这么有效呢?事实证明,交叉熵损失是由概率论证明的。
以下部分超出了范围,但肯定是一个有趣的阅读!
22.4.1 建立直觉:抛硬币
为了对逻辑回归建立一些直觉,让我们看一个分类的入门例子:抛硬币。假设我们观察到一些抛硬币的结果(1 = 正面,0 = 反面)。
flips = [0, 0, 1, 1, 1, 1, 0, 0, 0, 0]
flips
[0, 0, 1, 1, 1, 1, 0, 0, 0, 0]
一个合理的模型是假设所有的翻转都是独立同分布的(独立且同分布)。换句话说,每次翻转都有相同的概率返回 1(或正面)。让我们定义一个参数 θ \theta θ,即下一次翻转是正面的概率。我们将使用这个参数来决定我们对下一次翻转的 y ^ \hat y y^(预测为 0 或 1)。如果 θ ≥ 0.5 , y ^ = 1 , else y ^ = 0 \theta \ge 0.5, \hat y = 1, \text{else } \hat y = 0 θ≥0.5,y^=1,else y^=0。
你可能会倾向于说 θ = 0.5 \theta = 0.5 θ=0.5是最好的选择。然而,请注意我们对硬币本身没有做任何假设。硬币可能是有偏的,所以我们应该只基于数据做出决定。我们知道确切地有 4 10 \frac{4}{10} 104的翻转是正面,所以我们可能猜测 θ ^ = 0.4 \hat \theta = 0.4 θ^=0.4。在下一节中,我们将在数学上证明为什么这是最佳估计。
22.4.2 数据的可能性
让我们把硬币翻转的结果称为随机变量 Y Y Y。这是一个有两个结果的伯努利随机变量。 Y Y Y有以下分布:
P ( Y = y ) = { p , if y = 1 1 − p , if y = 0 P(Y = y) = \begin{cases} p, \text{if } y=1\\ 1 - p, \text{if } y=0 \end{cases} P(Y=y)={p,if y=11−p,if y=0
p p p对我们来说是未知的。但我们可以找到使我们观察到的数据最可能的 p p p。
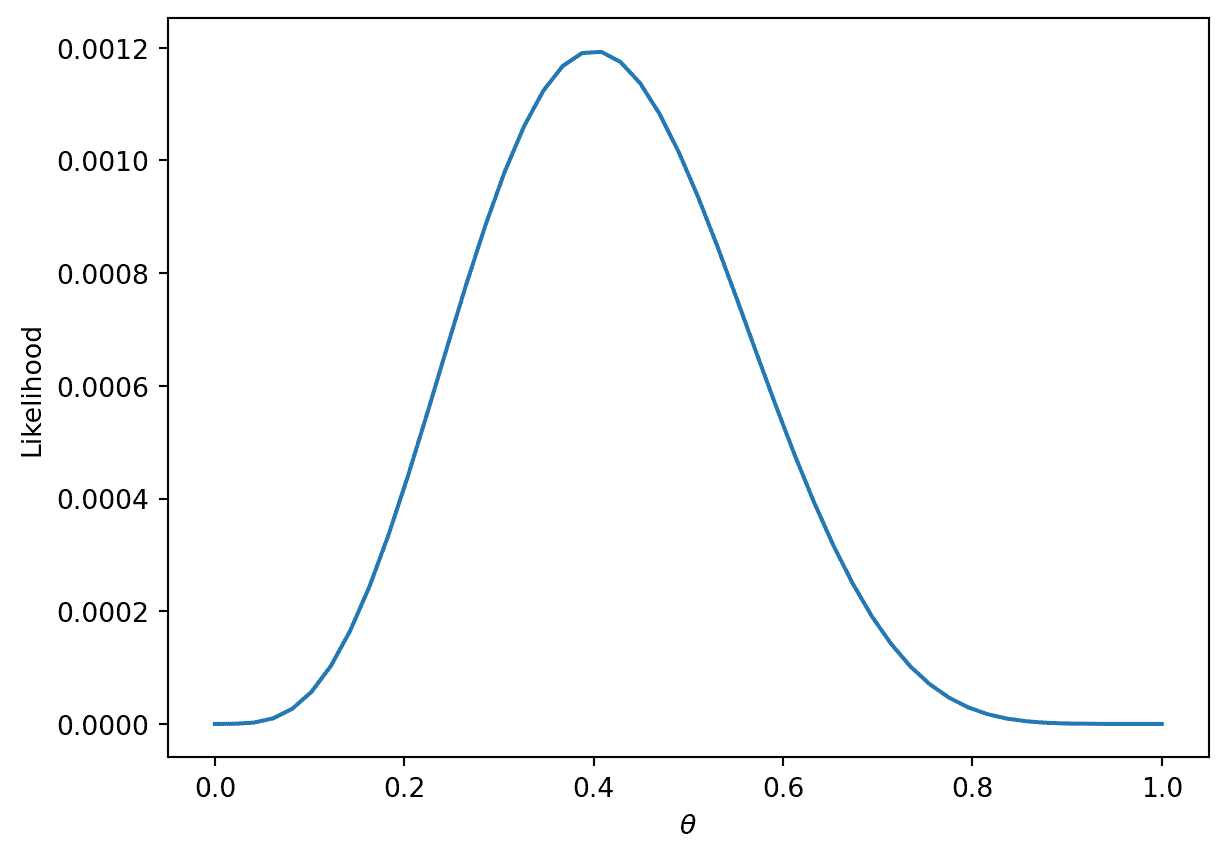
观察到 4 个正面和 6 个反面的概率遵循二项分布。
( 10 4 ) ( p ) 4 ( 1 − p ) 6 \binom{10}{4} (p)^4 (1-p)^6 (410)(p)4(1−p)6
我们定义获得我们观察到的数据的可能性,作为与上述概率成比例的数量。要找到它,只需将获得每个硬币翻转的概率相乘。
( p ) 4 ( 1 − p ) 6 (p)^{4} (1-p)^6 (p)4(1−p)6
称为最大似然估计的技术找到了最大化上述可能性的 p p p。你可以通过对可能性求导来找到这个最大值,但我们将提供一个更直观的图形解决方案。
thetas = np.linspace(0, 1)
plt.plot(thetas, (thetas**4)*(1-thetas)**6)
plt.xlabel(r"$\theta$")
plt.ylabel("Likelihood");
更一般地,对于某个伯努利( p p p)随机变量 Y Y Y的可能性是:
P ( Y = y ) = { 1 , with probability p 0 , with probability 1 − p P(Y = y) = \begin{cases} 1, \text{with probability } p\\ 0, \text{with probability } 1 - p \end{cases} P(Y=y)={1,with probability p0,with probability 1−p
等价地,这可以用一种简洁的方式来写:
P ( Y = y ) = p y ( 1 − p ) 1 − y P(Y=y) = p^y(1-p)^{1-y} P(Y=y)=py(1−p)1−y
-
当 y = 1 y = 1 y=1时,这读作 P ( Y = y ) = p P(Y=y) = p P(Y=y)=p
-
当 y = 0 y = 0 y=0时,这读作 P ( Y = y ) = ( 1 − p ) P(Y=y) = (1-p) P(Y=y)=(1−p)
在我们的例子中,伯努利随机变量类似于一个单个数据点(例如,篮球队赢得或输掉一场比赛的一个实例)。所有在一起,我们的games数据由许多 IID 伯努利( p p p)随机变量组成。要找到连续独立事件的可能性,只需将它们的可能性相乘。
∏ i = 1 n p y i ( 1 − p ) 1 − y i \prod_{i=1}^{n} p^{y_i} (1-p)^{1-y_i} i=1∏npyi(1−p)1−yi
与硬币的例子一样,我们想找到最大化这种可能性的参数 p p p。之前,我们给出了一个直观的图形解决方案,但让我们对可能性的导数进行求解以找到这个最大值。
乍一看,这个导数会很复杂!我们将不得不使用乘法规则,然后是链式法则。相反,我们可以做一个简化问题的观察。
找到最大化 ∏ i = 1 n p y i ( 1 − p ) 1 − y i \prod_{i=1}^{n} p^{y_i} (1-p)^{1-y_i} i=1∏npyi(1−p)1−yi的 p p p等同于最大化 log ( ∏ i = 1 n p y i ( 1 − p ) 1 − y i ) \text{log}(\prod_{i=1}^{n} p^{y_i} (1-p)^{1-y_i}) log(i=1∏npyi(1−p)1−yi)
这是因为 log \text{log} log是一个严格增加的函数。它不会改变它所应用的函数的最大值或最小值。根据 log \text{log} log的性质, log ( a ∗ b ) \text{log}(a*b) log(a∗b) = log ( a ) + log ( b ) \text{log}(a) + \text{log}(b) log(a)+log(b)。我们可以将这应用到我们上面的方程中得到:
= argmax p ∑ i = 1 n log ( p y i ( 1 − p ) 1 − y i ) =\underset{p}{\text{argmax}} \sum_{i=1}^{n} \text{log}(p^{y_i} (1-p)^{1-y_i}) =pargmaxi=1∑nlog(pyi(1−p)1−yi)
= argmax p ∑ i = 1 n ( log ( p y i ) + log ( ( 1 − p ) 1 − y i ) ) = \underset{p}{\text{argmax}} \sum_{i=1}^{n} (\text{log}(p^{y_i}) + \text{log}((1-p)^{1-y_i})) =pargmaxi=1∑n(log(pyi)+log((1−p)1−yi))
= argmax p ∑ i = 1 n ( y i log ( p ) + ( 1 − y i ) log ( 1 − p ) ) = \underset{p}{\text{argmax}} \sum_{i=1}^{n} (y_i\text{log}(p) + (1-y_i)\text{log}(1-p)) =pargmaxi=1∑n(yilog(p)+(1−yi)log(1−p))
我们可以在前面添加一个常数因子 1 n \frac{1}{n} n1。这不会影响最大化我们的似然性的 p p p。
= argmax p 1 n ∑ i = 1 n y i log ( p ) + ( 1 − y i ) log ( 1 − p ) =\underset{p}{\text{argmax}} \frac{1}{n} \sum_{i=1}^{n} y_i\text{log}(p) + (1-y_i)\text{log}(1-p) =pargmaxn1i=1∑nyilog(p)+(1−yi)log(1−p)
我们可以做的最后一个“技巧”是通过取反来将其转换为最小化问题。这是因为我们正在处理一个凹函数,可以将其变为凸函数。
= argmin p − 1 n ∑ i = 1 n y i log ( p ) + ( 1 − y i ) log ( 1 − p ) = \underset{p}{\text{argmin}} -\frac{1}{n} \sum_{i=1}^{n} y_i\text{log}(p) + (1-y_i)\text{log}(1-p) =pargmin−n1i=1∑nyilog(p)+(1−yi)log(1−p)
现在假设我们有独立的具有不同概率 p i p_i pi的数据。那么,我们希望找到最大化 ∏ i = 1 n p i y i ( 1 − p i ) 1 − y i \prod_{i=1}^{n} p_i^{y_i} (1-p_i)^{1-y_i} i=1∏npiyi(1−pi)1−yi的 p 1 , p 2 , … , p n p_1, p_2, \dots, p_n p1,p2,…,pn。
像我们上面那样设置和简化优化问题,我们最终想要找到:
= argmin p − 1 n ∑ i = 1 n y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) = \underset{p}{\text{argmin}} -\frac{1}{n} \sum_{i=1}^{n} y_i\text{log}(p_i) + (1-y_i)\text{log}(1-p_i) =pargmin−n1i=1∑nyilog(pi)+(1−yi)log(1−pi)
对于逻辑回归, p i = σ ( x ⊤ θ ) p_i = \sigma(x^{\top}\theta) pi=σ(x⊤θ)。将其代入,我们得到:
= argmin p − 1 n ∑ i = 1 n y i log ( σ ( x ⊤ θ ) ) + ( 1 − y i ) log ( 1 − σ ( x ⊤ θ ) ) = \underset{p}{\text{argmin}} -\frac{1}{n} \sum_{i=1}^{n} y_i\text{log}(\sigma(x^{\top}\theta)) + (1-y_i)\text{log}(1-\sigma(x^{\top}\theta)) =pargmin−n1i=1∑nyilog(σ(x⊤θ))+(1−yi)log(1−σ(x⊤θ))
这正是我们之前讨论过的平均交叉熵损失最小化问题!
为什么我们要做这么复杂的数学?我们已经证明最小化交叉熵损失等价于最大化训练数据的似然性。
- 通过最小化交叉熵损失,我们选择了对我们观察到的数据“最有可能”的模型参数。
请注意,这是在所有数据都是独立地从相同的逻辑回归模型中抽取的假设下。事实上,我们所见过的许多模型+损失组合都可以通过最大似然估计来解释(例如 OLS,岭回归等)。在概率和机器学习课程中,你将有机会进一步探讨最大似然估计。
二十三、逻辑回归 II
原文:Logistic Regression II
译者:飞龙
协议:CC BY-NC-SA 4.0
学习成果
-
应用决策规则进行分类
-
了解逻辑回归何时运行良好,何时不运行良好
-
引入模型性能的新指标
今天,我们将继续学习逻辑回归模型。我们将讨论决策边界,以帮助确定特定预测的分类。然后,我们将从上次讲座关于交叉熵损失的讨论中继续学习一些问题,并学习潜在的解决方法。我们还将提供sklearn逻辑回归模型的实现。最后,我们将回到决策规则,并讨论允许我们在不同情况下确定模型性能的指标。
这将使我们了解阈值处理的过程 - 一种用于从模型预测的概率或 P ( Y = 1 ∣ x ) P(Y=1|x) P(Y=1∣x)对数据进行分类的技术。在这样做时,我们将重点关注这些阈值决策如何影响我们模型的行为。我们将学习对二元分类有用的各种评估指标,并将它们应用于我们对逻辑回归的研究中。
23.1 决策边界
在逻辑回归中,我们建模数据点属于类别 1 的概率。上周,我们开发了逻辑回归模型来预测该概率,但我们实际上并没有对我们的预测 y y y属于类别 0 还是类别 1 进行任何分类。
p = P ( Y = 1 ∣ x ) = 1 1 + e − x T θ p = P(Y=1 | x) = \frac{1}{1 + e^{-x^T\theta}} p=P(Y=1∣x)=1+e−xTθ1
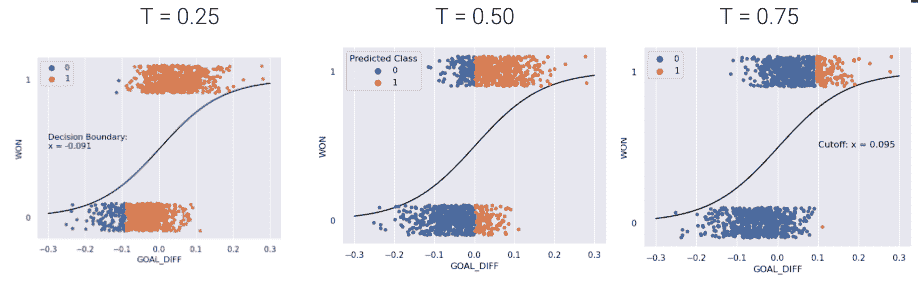
决策规则告诉我们如何解释模型的输出,以便对数据点进行分类。我们通常通过指定阈值 T T T来制定决策规则。如果预测概率大于或等于 T T T,则预测为类别 1。否则,预测为类别 0。
y ^ = classify ( x ) = { 1 , P ( Y = 1 ∣ x ) ≥ T 0 , otherwise \hat y = \text{classify}(x) = \begin{cases} 1, & P(Y=1|x) \ge T\\ 0, & \text{otherwise } \end{cases} y^=classify(x)={1,0,P(Y=1∣x)≥Totherwise
阈值通常设置为 T = 0.5 T = 0.5 T=0.5,但并非总是如此。我们将讨论为什么我们可能希望在本讲座后期使用其他阈值 T ≠ 0.5 T \neq 0.5 T=0.5。
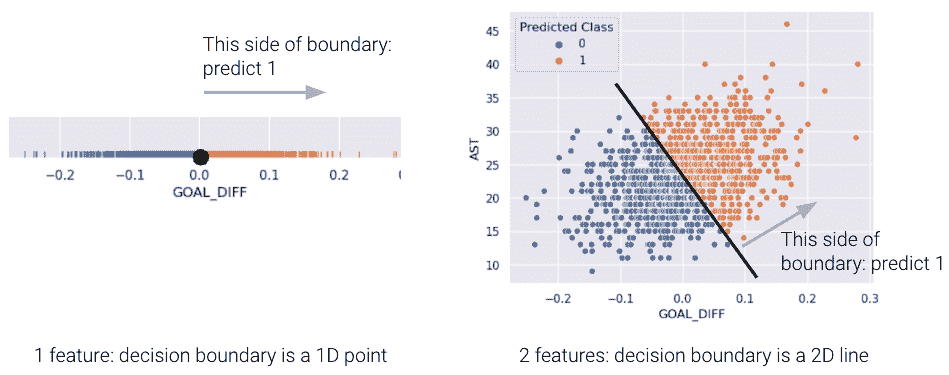
使用我们的决策规则,我们可以将决策边界定义为根据其特征将数据分成类的“线”。对于逻辑回归,决策边界是一个超平面 - 特征在 p 维中的线性组合 - 我们可以从最终的逻辑回归模型中恢复它。例如,如果我们有一个具有 2 个特征(2D)的模型,我们有 θ = [ θ 0 , θ 1 , θ 2 ] \theta = [\theta_0, \theta_1, \theta_2] θ=[θ0,θ1,θ2] 包括截距项,并且我们可以这样解决决策边界:
T = 1 1 + e − ( θ 0 + θ 1 ∗ feature1 + θ 2 ∗ feature2 ) 1 + e − ( θ 0 + θ 1 ⋅ feature1 + θ 2 ⋅ feature2 ) = 1 T e − ( θ 0 + θ 1 ⋅ feature1 + θ 2 ⋅ feature2 ) = 1 T − 1 θ 0 + θ 1 ⋅ feature1 + θ 2 ⋅ feature2 = − log ( 1 T − 1 ) \begin{align} T &= \frac{1}{1 + e^{-(\theta_0 + \theta_1 * \text{feature1} + \theta_2 * \text{feature2})}} \\ 1 + e^{-(\theta_0 + \theta_1 \cdot \text{feature1} + \theta_2 \cdot \text{feature2})} &= \frac{1}{T} \\ e^{-(\theta_0 + \theta_1 \cdot \text{feature1} + \theta_2 \cdot \text{feature2})} &= \frac{1}{T} - 1 \\ \theta_0 + \theta_1 \cdot \text{feature1} + \theta_2 \cdot \text{feature2} &= -\log(\frac{1}{T} - 1) \end{align} T1+e−(θ0+θ1⋅feature1+θ2⋅feature2)e−(θ0+θ1⋅feature1+θ2⋅feature2)θ0+θ1⋅feature1+θ2⋅feature2=1+e−(θ0+θ1∗feature1+θ2∗feature2)1=T1=T1−1=−log(T1−1)
对于具有 2 个特征的模型,决策边界是根据其特征的一条线。为了更容易可视化,我们在下面包括了一个一维和一个二维决策边界的示例。请注意,我们的逻辑回归模型预测的决策边界完美地将点分成了两类。
然而,在现实生活中,情况通常并非如此,我们经常看到不同类别的点在决策边界上有一些重叠。2D 数据的真实类如下所示:
正如你所看到的,我们的逻辑回归预测的决策边界并不能完全将两个类别分开。在决策边界附近有一个“混乱”的区域,我们的分类器会预测错误的类别。数据看起来会是什么样子,使得分类器能够做出完美的预测呢?
23.2 线性可分性和正则化
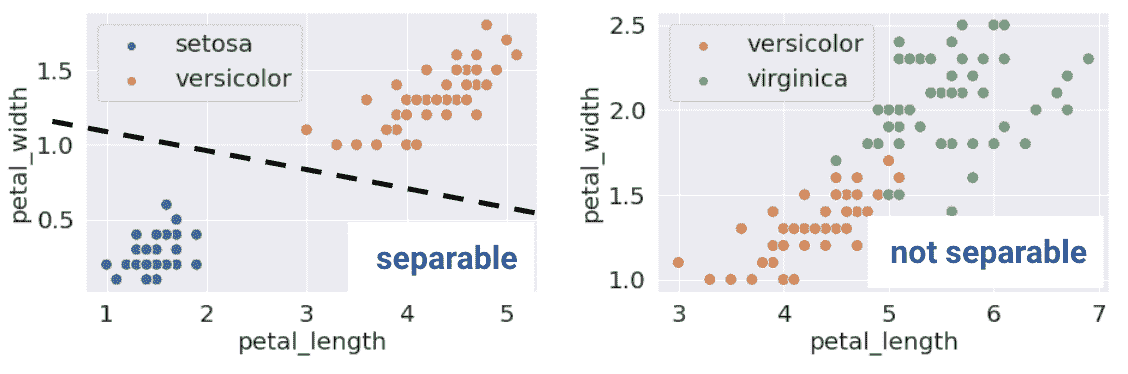
如果存在一个超平面可以将输入特征 x x x分开两个类别 y y y,那么分类数据集就被称为线性可分。
在 1D 中的线性可分性可以通过单个特征的 rugplot 来找到。例如,注意左下角的图是沿着垂直线 x = 0 x=0 x=0线性可分的。然而,在右下角,没有这样的线可以完美地将两个类别分开。
这个定义在更高的维度中也是成立的。如果有两个特征,分离的超平面必须存在于两个维度中(任何形式为 y = m x + b y=mx+b y=mx+b的直线)。我们可以使用散点图来可视化这一点。
听起来很棒!当数据集是线性可分的时候,逻辑回归分类器可以完美地将数据点分配到类别中。然而,(意想不到的)复杂性可能会出现。考虑具有 2 个点和仅一个特征 x x x的“玩具”数据集:
最小化损失的最佳 θ \theta θ值将数据点的预测概率推向其真实类别。
-
P ( Y = 1 ∣ x = − 1 ) = 1 1 + e θ → 1 P(Y = 1|x = -1) = \frac{1}{1 + e^\theta} \rightarrow 1 P(Y=1∣x=−1)=1+eθ1→1
-
P ( Y = 1 ∣ x = 1 ) = 1 1 + e − θ → 0 P(Y = 1|x = 1) = \frac{1}{1 + e^{-\theta}} \rightarrow 0 P(Y=1∣x=1)=1+e−θ1→0
当 θ = − ∞ \theta = -\infty θ=−∞时会发生这种情况。当 θ = − ∞ \theta = -\infty θ=−∞时,我们观察到对于任何输入 x x x的以下行为。
P ( Y = 1 ∣ x ) = σ ( θ x ) → { 1 , if x < 0 0 , if x ≥ 0 P(Y=1|x) = \sigma(\theta x) \rightarrow \begin{cases} 1, \text{if } x < 0\\ 0, \text{if } x \ge 0 \end{cases} P(Y=1∣x)=σ(θx)→{1,if x<00,if x≥0
权重的发散会导致模型过度自信。例如,考虑新的点 ( x , y ) = ( 0.5 , 1 ) (x, y) = (0.5, 1) (x,y)=(0.5,1)。根据上面的行为,我们的模型会错误地预测 p = 0 p=0 p=0,因此 y ^ = 0 \hat y = 0 y^=0。
这个错误分类点所产生的损失是无穷大的。
− ( y log ( p ) + ( 1 − y ) log ( 1 − p ) ) = 1 log ( 0 ) -(y\text{ log}(p) + (1-y)\text{ log}(1-p))=1\text{log}(0) −(y log(p)+(1−y) log(1−p))=1log(0)
因此,权重发散( ∣ θ ∣ → ∞ |\theta| \rightarrow \infty ∣θ∣→∞)会出现在线性可分数据中。“过度自信”是过度拟合的一个特别危险的版本。
考虑损失函数关于参数 θ \theta θ的情况。
虽然很难看到,但是对于 θ \theta θ的负值,损失函数的平台略微向下倾斜,这意味着当 θ \theta θ减小并趋近于 − ∞ -\infty −∞时,损失趋近于 0 0 0。
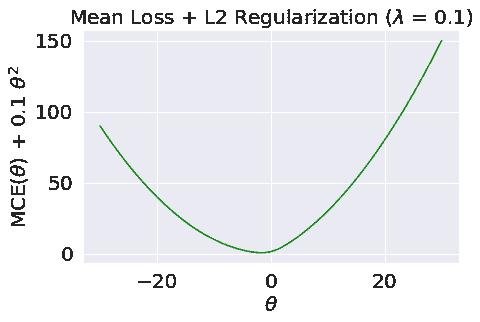
23.2.1 正则化逻辑回归
为了避免大的权重和无穷大的损失(特别是在线性可分的数据上),我们使用正则化。与线性回归一样,同样的原则适用-首先确保标准化你的特征。
例如, L 2 L2 L2(Ridge)逻辑回归的形式如下:
min θ − 1 n ∑ i = 1 n ( y i log ( σ ( x i T θ ) ) + ( 1 − y i ) log ( 1 − σ ( x i T θ ) ) ) + λ ∑ i = 1 d θ j 2 \min_{\theta} -\frac{1}{n} \sum_{i=1}^{n} (y_i \text{log}(\sigma(x_i^T\theta)) + (1-y_i)\text{log}(1-\sigma(x_i^T\theta))) + \lambda \sum_{i=1}^{d} \theta_j^2 θmin−n1i=1∑n(yilog(σ(xiTθ))+(1−yi)log(1−σ(xiTθ)))+λi=1∑dθj2
现在,让我们比较未正则化和正则化逻辑回归的损失函数。
正如我们所看到的, L 2 L2 L2正则化有助于防止权重发散,并且防止“过度自信”。
sklearn的逻辑回归默认使用 L2 正则化和C=1.0;C是 λ \lambda λ的倒数: C = 1 λ C = \frac{1}{\lambda} C=λ1。将C设置为一个大的值,例如C=300.0,会导致最小的正则化。
# sklearn defaults
model = LogisticRegression(penalty='l2', C=1.0, …)
model.fit()
请注意,在 Data 100 中,我们只使用sklearn来拟合逻辑回归模型。对于最优的 theta 向量,没有封闭形式的解,梯度有点混乱(有关详细信息,请参见下面的奖励部分)。
从这里,.predict 函数返回点的预测类别 y ^ \hat y y^。在简单的二进制情况下,
y ^ = { 1 , P ( Y = 1 ∣ x ) ≥ 0.5 0 , 否则 \hat y = \begin{cases} 1, & P(Y=1|x) \ge 0.5\\ 0, & \text{否则 } \end{cases} y^={1,0,P(Y=1∣x)≥0.5否则
23.3 性能指标
你可能会想,如果我们已经引入了交叉熵损失,为什么我们还需要额外的方法来评估我们的模型表现如何呢?在线性回归中,我们进行了数值预测,并使用损失函数来确定这些预测的“好坏”。在逻辑回归中,我们的最终目标是对数据进行分类 - 我们更关心每个数据点是否使用决策规则分配了正确的类。因此,我们对分类的质量感兴趣,而不是预测的概率。
最基本的评估指标是准确率,即被正确分类的点的比例。
准确率 = # 分类正确的点 # 总点数 \text{准确率} = \frac{\# \text{分类正确的点}}{\# \text{总点数}} 准确率=#总点数#分类正确的点
翻译成代码:
def accuracy(X, Y):
return np.mean(model.predict(X) == Y)
model.score(X, y) # built-in accuracy function
然而,准确率并不总是分类的一个很好的指标。要理解为什么,让我们考虑一个分类问题,有 100 封电子邮件,其中只有 5 封是真正的垃圾邮件,其余 95 封是真正的非垃圾邮件。我们将研究两个准确率不佳的模型。
-
模型 1:我们的第一个模型将每封电子邮件都分类为非垃圾邮件。模型的准确率很高( 95 100 = 0.95 \frac{95}{100} = 0.95 10095=0.95),但它没有检测到任何垃圾邮件。尽管准确率很高,但这是一个糟糕的模型。
-
模型 2:第二个模型将每封电子邮件都分类为垃圾邮件。准确率低( 5 100 = 0.05 \frac{5}{100} = 0.05 1005=0.05),但模型正确标记了每封垃圾邮件。不幸的是,它也错误分类了每封非垃圾邮件。
正如这个例子所说明的,准确率并不总是分类的一个很好的指标,特别是当你的数据可能表现出类别不平衡时(例如,1 的数量很少相对于 0)。
23.3.1 分类类型
我们的模型可能做出 4 种不同的分类:
-
真正例:将正点正确分类为正( y = 1 y=1 y=1 和 y ^ = 1 \hat{y}=1 y^=1)
-
真负例:将负点正确分类为负( y = 0 y=0 y=0 和 y ^ = 0 \hat{y}=0 y^=0)
-
假正例:将负点错误分类为正( y = 0 y=0 y=0 和 y ^ = 1 \hat{y}=1 y^=1)
-
假负例:将正点错误分类为负( y = 1 y=1 y=1 和 y ^ = 0 \hat{y}=0 y^=0)
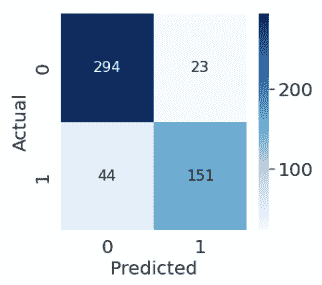
这些分类可以简洁地总结在一个混淆矩阵中。
记住这个术语的一个简单方法如下:
-
看短语中的第二个词。正 意味着预测为 1。负 意味着预测为 0。
-
看短语中的第一个词。真 意味着我们的预测是正确的。假 意味着它是错误的。
现在我们可以将准确率计算写成 准确率 = T P + T N n \text{准确率} = \frac{TP + TN}{n} 准确率=nTP+TN
在sklearn中,我们使用以下语法
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(Y_true, Y_pred)
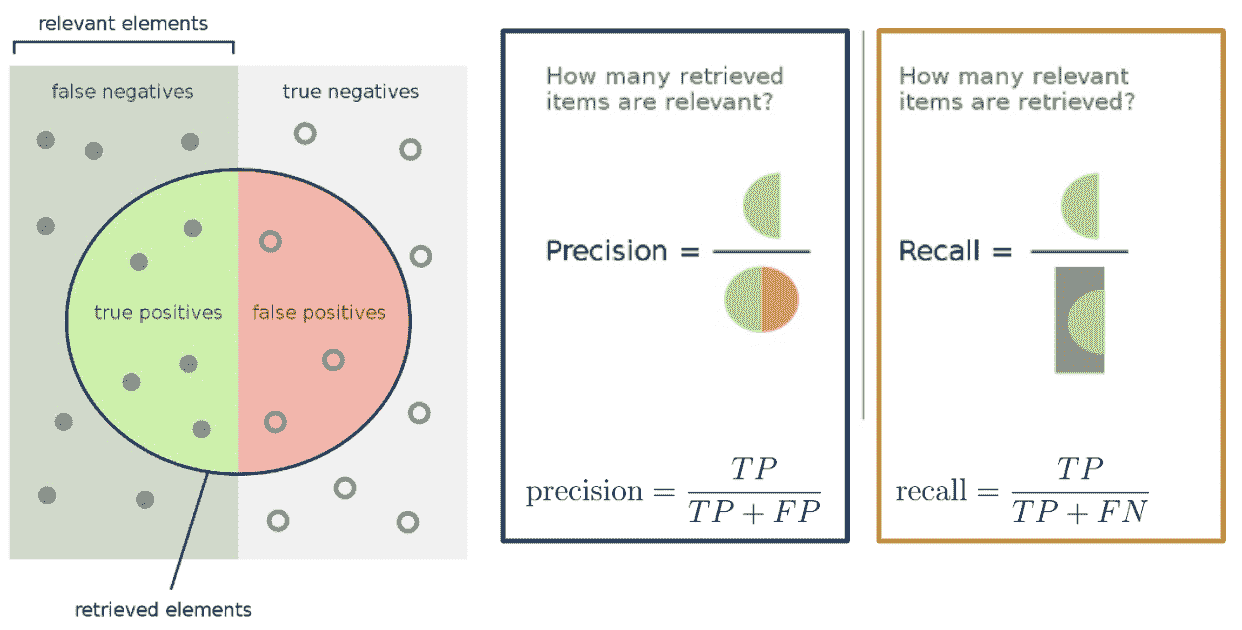
23.3.2 准确率、精度和召回率
我们讨论混淆矩阵的目的是激发对于具有类别不平衡的分类问题的更好的性能指标 - 即精度和召回率。
精度 定义为
精度 = TP TP + FP \text{精度} = \frac{\text{TP}}{\text{TP + FP}} 精度=TP + FPTP
精度回答了这个问题:“在所有被预测为 1 1 1 的观察中,有多少比例实际上是 1 1 1?”它衡量了分类器在其预测为正时的准确性。
召回率(或敏感度)定义为
召回率 = TP TP + FN \text{召回率} = \frac{\text{TP}}{\text{TP + FN}} 召回率=TP + FNTP
召回旨在回答:“实际上是 1 1 1的所有观察中,有多少被预测为 1 1 1?”它衡量了有多少积极的预测被忽略了。
以下是一个有用的图表,总结了我们上面的讨论。
23.3.3 示例计算
在本节中,我们将计算我们之前的垃圾邮件分类示例的准确性、精度和召回率性能指标。作为提醒,我们有 100 封电子邮件,其中有 5 封是垃圾邮件。我们设计了两个模型:
-
模型 1:预测每封电子邮件都是非垃圾邮件
-
模型 2:预测每封电子邮件都是垃圾邮件
23.3.3.1 模型 1
首先,让我们从创建混淆矩阵开始。
| 0 | 1 | |
|---|---|---|
| 0 | 真阴性:95 | 假阳性:0 |
| 1 | 假阴性:5 | 真阳性:0 |
说服自己为什么我们的混淆矩阵看起来像这样。
准确性 = 95 100 = 0.95 \text{准确性} = \frac{95}{100} = 0.95 准确性=10095=0.95
精度 = 0 0 + 0 = 未定义 \text{精度} = \frac{0}{0 + 0} = \text{未定义} 精度=0+00=未定义
召回率 = 0 0 + 5 = 0 \text{召回率} = \frac{0}{0 + 5} = 0 召回率=0+50=0
注意我们的精度是未定义的,因为我们从未预测过类 1 1 1。由于相同的原因,我们的召回率为 0-分子为 0(我们没有积极的预测)。
23.3.3.2 模型 2
我们的模型 2 的混淆矩阵如下。
| 0 | 1 | |
|---|---|---|
| 0 | 真阴性:0 | 假阳性:95 |
| 1 | 假阴性:0 | 真阳性:5 |
准确性 = 5 100 = 0.05 \text{准确性} = \frac{5}{100} = 0.05 准确性=1005=0.05
精度 = 5 5 + 95 = 0.05 \text{精度} = \frac{5}{5 + 95} = 0.05 精度=5+955=0.05
召回率 = 5 5 + 0 = 1 \text{召回率} = \frac{5}{5 + 0} = 1 召回率=5+05=1
我们的精度很低,因为我们有很多假阳性,而我们的召回率是完美的-我们正确分类了所有的垃圾邮件(我们从未预测过类 0 0 0)。
23.3.4 精度与召回率
精度( TP TP + FP \frac{\text{TP}}{\text{TP} + \textbf{ FP}} TP+ FPTP)惩罚假阳性,而召回率( TP TP + FN \frac{\text{TP}}{\text{TP} + \textbf{ FN}} TP+ FNTP)惩罚假阴性。
事实上,精度和召回率是相互关联的。这在我们的第二个模型中是明显的-我们观察到召回率高,精度低。通常,这两者之间存在权衡(大多数模型可以最小化 FP 或 FN 的数量;在少数情况下,两者都可以)。
要优先考虑的具体性能指标取决于上下文。在许多医疗环境中,错过阳性病例可能会带来更高的成本。例如,在我们的乳腺癌示例中,误将恶性肿瘤分类为良性肿瘤(假阳性)的成本更高,而不是将良性肿瘤错误地分类为恶性肿瘤(假阴性)。在后一种情况下,病理学家可以进行进一步的研究以验证恶性肿瘤。因此,我们应该最小化假阴性的数量。这等同于最大化召回率。
23.3.5 另外两个指标
**真阳性率(TPR)**定义为
真阳性率 = TP TP + FN \text{真阳性率} = \frac{\text{TP}}{\text{TP + FN}} 真阳性率=TP + FNTP
您会注意到这等同于召回率。在我们的垃圾邮件分类器的背景下,它回答了一个问题:“我标记了多少垃圾邮件是正确的?”。我们希望这个数字接近 1 1 1
**假阳性率(FPR)**定义为
假阳性率 = FP FP + TN \text{假阳性率} = \frac{\text{FP}}{\text{FP + TN}} 假阳性率=FP + TNFP
FPR 的另一个词是特异性。这回答了一个问题:“我将多少常规邮件标记为垃圾邮件?”。我们希望这个数字接近 0 0 0
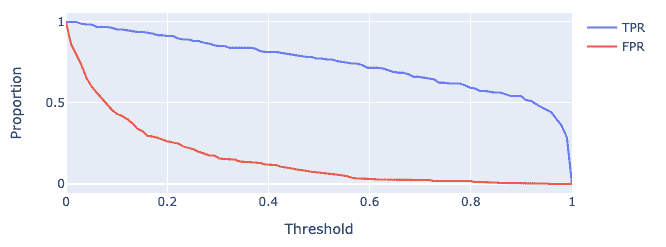
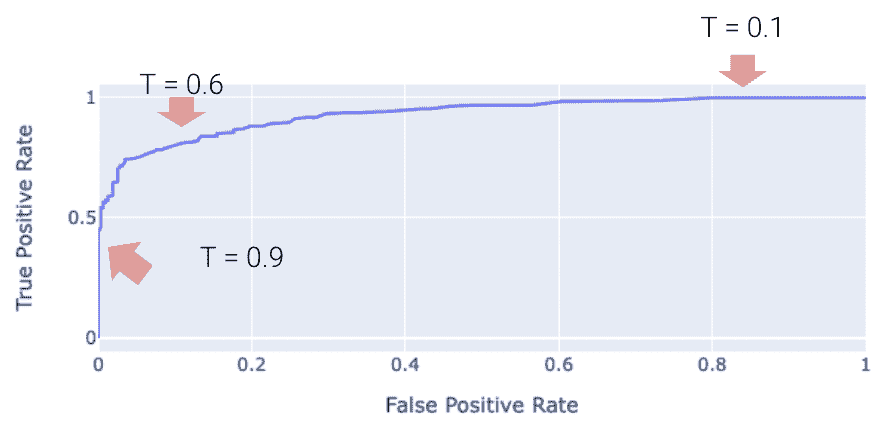
随着阈值 T T T的增加,TPR 和 FPR 都会减少。我们在下面为某个toy数据集上的某个模型绘制了这种关系。
23.4 调整分类阈值
最小化 FP 与 FN 的数量(等效地,最大化精度与召回率)的一种方法是调整分类阈值 T T T。
y ^ = { 1 , P ( Y = 1 ∣ x ) ≥ T 0 , otherwise \hat y = \begin{cases} 1, & P(Y=1|x) \ge T\\ 0, & \text{otherwise } \end{cases} y^={1,0,P(Y=1∣x)≥Totherwise
sklearn中的默认阈值为 T = 0.5 T = 0.5 T=0.5。当我们增加阈值 T T T时,我们“提高了标准”,即我们的分类器需要预测 1(即“积极”)的信心有多大。
正如您可能注意到的,阈值 T T T的选择会影响我们的分类器的性能。
-
高 T T T:大多数预测为 0 0 0。
-
更多的假阴性
-
更少的假阳性
-
-
低 T T T:大多数预测为 1 1 1。
-
更多的假阳性
-
更少的假阴性
-
事实上,我们可以根据我们期望的假阳性和假阴性的数量或比例选择一个阈值 T T T。我们可以使用一些不同的工具来做到这一点。我们将在 Data 100 中介绍其中两个最重要的工具。
-
精确-召回曲线(PR 曲线)
-
“受试者工作特征”曲线(ROC 曲线)
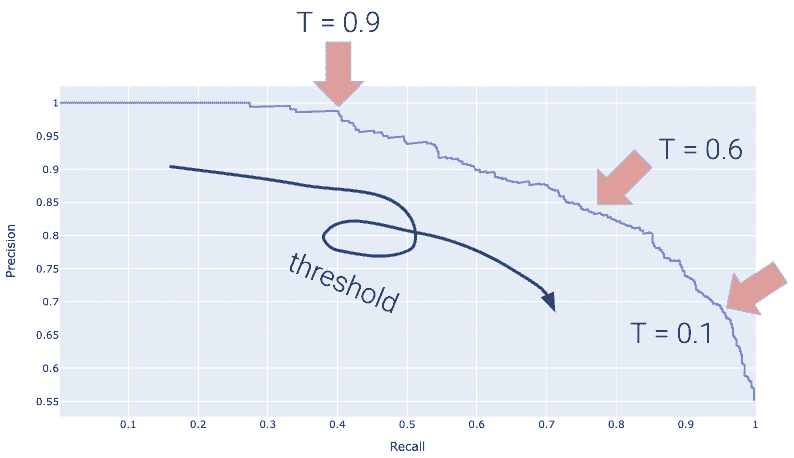
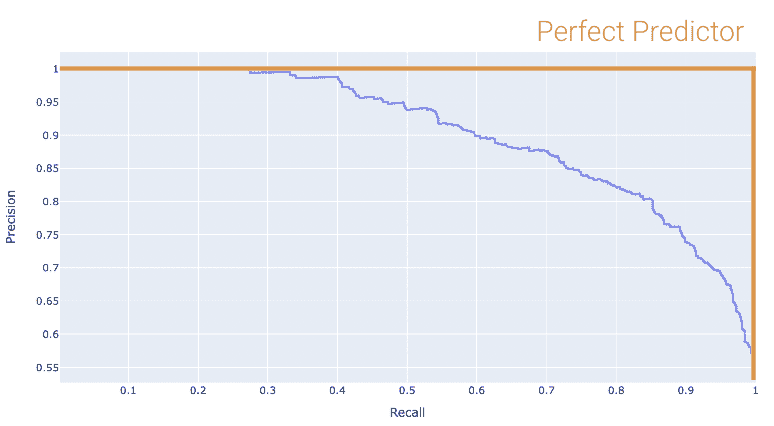
23.4.1 精确-召回曲线
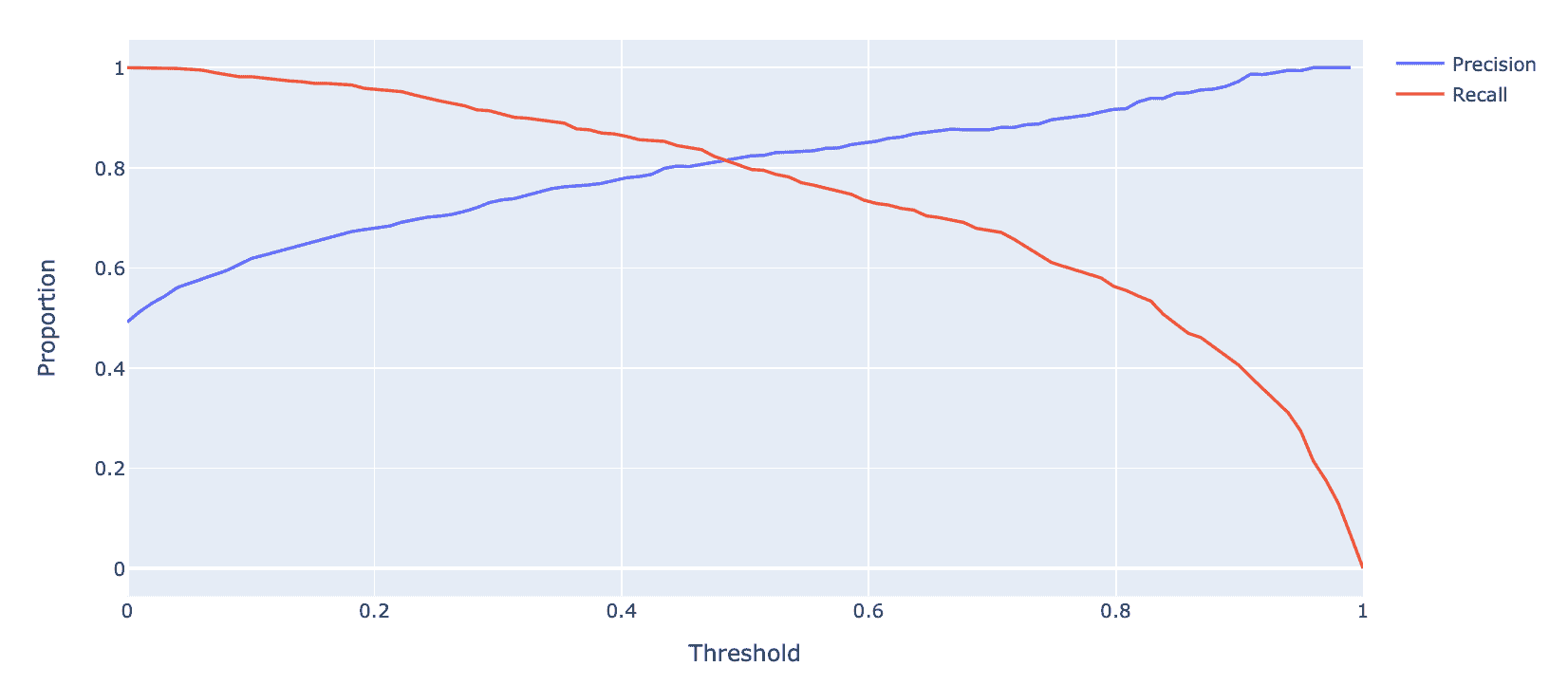
**精确-召回曲线(PR 曲线)**是 ROC 曲线的替代品,显示了不同阈值的精确度和召回率之间的关系。它的构造方式与 ROC 曲线类似。
让我们首先考虑精确度和召回率如何随阈值 T T T的变化而变化。我们从前面很清楚 - 精确度通常会增加,召回率会减少。
下面显示的是相同toy数据集的 PR 曲线。注意随着我们向左移动,阈值值会增加。
再次,完美的分类器将类似于橙色曲线,这次朝着相反的方向。
我们希望我们的 PR 曲线尽可能接近这张图的“右上角”。同样,我们使用 AUC 来确定“接近度”,完美的分类器表现为 AUC = 1(最差的为 AUC = 0.5)。
23.4.2 ROC 曲线
“受试者工作特征”曲线(ROC 曲线)绘制了 FPR 和 TPR 之间的权衡。注意曲线的最左侧对应于较高的阈值 T T T值。
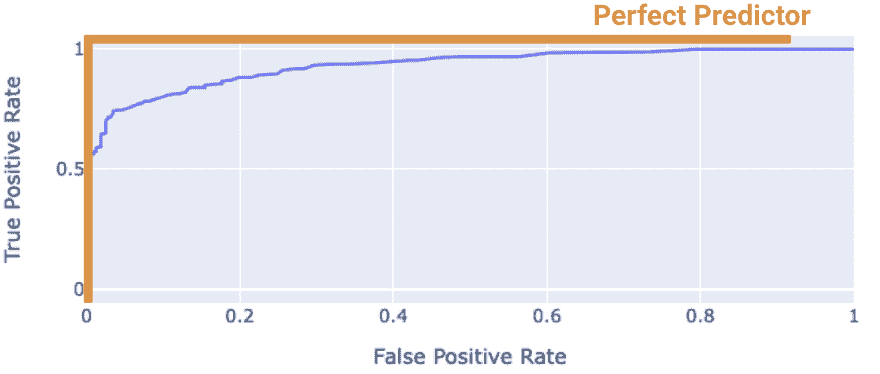
“完美”的分类器是具有 TPR = 1 和 FPR = 0 的分类器。这是在下面图中的左上角实现的。更一般地,它的 ROC 曲线类似于橙色曲线。
我们希望我们的模型尽可能接近这条橙色曲线。我们如何量化“接近度”?
我们可以计算 ROC 曲线下的曲线下面积(AUC)。注意完美分类器的 AUC = 1。我们的模型的 AUC 越接近 1,它就越好。
23.4.2.1(奖励)什么是“最差”的 AUC,为什么是 0.5?
另一方面,糟糕的模型的 AUC 将更接近 0.5。随机预测器随机预测 P ( Y = 1 ∣ x ) P(Y = 1 | x) P(Y=1∣x)在 0 和 1 之间均匀分布。这表明分类器无法区分正类和负类,因此随机预测其中之一。
23.5(奖励)逻辑回归的梯度下降
让我们定义以下: t i = ϕ ( x i ) T θ p i = σ ( t i ) t i = log ( p i 1 − p i ) 1 − σ ( t i ) = σ ( − t i ) d d t σ ( t ) = σ ( t ) σ ( − t ) t_i = \phi(x_i)^T \theta \\ p_i = \sigma(t_i) \\ t_i = \log(\frac{p_i}{1 - p_i}) \\ 1 - \sigma(t_i) = \sigma(-t_i) \\ \frac{d}{dt} \sigma(t) = \sigma(t) \sigma(-t) ti=ϕ(xi)Tθpi=σ(ti)ti=log(1−pipi)1−σ(ti)=σ(−ti)dtdσ(t)=σ(t)σ(−t)
现在,我们可以简化交叉熵损失 y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) = y i log ( p i 1 − p i ) + log ( 1 − p i ) = y i ϕ ( x i ) T + log ( σ ( − ϕ ( x i ) T θ ) ) \begin{align} y_i \log(p_i) + (1 - y_i) \log(1 - p_i) &= y_i \log(\frac{p_i}{1 - p_i}) + \log(1 - p_i) \\ &= y_i \phi(x_i)^T + \log(\sigma(-\phi(x_i)^T \theta)) \end{align} yilog(pi)+(1−yi)log(1−pi)=yilog(1−pipi)+log(1−pi)=yiϕ(xi)T+log(σ(−ϕ(xi)Tθ))
因此,最佳的 θ ^ \hat{\theta} θ^是 argmin θ − 1 n ∑ i = 1 n ( y i ϕ ( x i ) T + log ( σ ( − ϕ ( x i ) T θ ) ) ) \text{argmin}_{\theta} - \frac{1}{n} \sum_{i=1}^n (y_i \phi(x_i)^T + \log(\sigma(-\phi(x_i)^T \theta))) argminθ−n1i=1∑n(yiϕ(xi)T+log(σ(−ϕ(xi)Tθ)))
我们希望最小化 L ( θ ) = − 1 n ∑ i = 1 n ( y i ϕ ( x i ) T + log ( σ ( − ϕ ( x i ) T θ ) ) ) L(\theta) = - \frac{1}{n} \sum_{i=1}^n (y_i \phi(x_i)^T + \log(\sigma(-\phi(x_i)^T \theta))) L(θ)=−n1i=1∑n(yiϕ(xi)T+log(σ(−ϕ(xi)Tθ)))
因此,我们对导数进行如下处理 ▽ θ L ( θ ) = − 1 n ∑ i = 1 n ▽ θ y i ϕ ( x i ) T + ▽ θ log ( σ ( − ϕ ( x i ) T θ ) ) = − 1 n ∑ i = 1 n y i ϕ ( x i ) + ▽ θ log ( σ ( − ϕ ( x i ) T θ ) ) = − 1 n ∑ i = 1 n y i ϕ ( x i ) + 1 σ ( − ϕ ( x i ) T θ ) ▽ θ σ ( − ϕ ( x i ) T θ ) = − 1 n ∑ i = 1 n y i ϕ ( x i ) + σ ( − ϕ ( x i ) T θ ) σ ( − ϕ ( x i ) T θ ) σ ( ϕ ( x i ) T θ ) ▽ θ σ ( − ϕ ( x i ) T θ ) = − 1 n ∑ i = 1 n ( y i − σ ( ϕ ( x i ) T θ ) ϕ ( x i ) ) \begin{align} \triangledown_{\theta} L(\theta) &= - \frac{1}{n} \sum_{i=1}^n \triangledown_{\theta} y_i \phi(x_i)^T + \triangledown_{\theta} \log(\sigma(-\phi(x_i)^T \theta)) \\ &= - \frac{1}{n} \sum_{i=1}^n y_i \phi(x_i) + \triangledown_{\theta} \log(\sigma(-\phi(x_i)^T \theta)) \\ &= - \frac{1}{n} \sum_{i=1}^n y_i \phi(x_i) + \frac{1}{\sigma(-\phi(x_i)^T \theta)} \triangledown_{\theta} \sigma(-\phi(x_i)^T \theta) \\ &= - \frac{1}{n} \sum_{i=1}^n y_i \phi(x_i) + \frac{\sigma(-\phi(x_i)^T \theta)}{\sigma(-\phi(x_i)^T \theta)} \sigma(\phi(x_i)^T \theta)\triangledown_{\theta} \sigma(-\phi(x_i)^T \theta) \\ &= - \frac{1}{n} \sum_{i=1}^n (y_i - \sigma(\phi(x_i)^T \theta)\phi(x_i)) \end{align} ▽θL(θ)=−n1i=1∑n▽θyiϕ(xi)T+▽θlog(σ(−ϕ(xi)Tθ))=−n1i=1∑nyiϕ(xi)+▽θlog(σ(−ϕ(xi)Tθ))=−n1i=1∑nyiϕ(xi)+σ(−ϕ(xi)Tθ)1▽θσ(−ϕ(xi)Tθ)=−n1i=1∑nyiϕ(xi)+σ(−ϕ(xi)Tθ)σ(−ϕ(xi)Tθ)σ(ϕ(xi)Tθ)▽θσ(−ϕ(xi)Tθ)=−n1i=1∑n(yi−σ(ϕ(xi)Tθ)ϕ(xi))
将导数设置为 0 并解出 θ ^ \hat{\theta} θ^,我们发现没有一般的解析解。因此,我们必须使用数值方法来解决。
23.5.1 梯度下降更新规则
θ ( 0 ) ← 初始向量(随机,零,...) \theta^{(0)} \leftarrow \text{初始向量(随机,零,...)} θ(0)←初始向量(随机,零,...)
对于从 0 到收敛的 τ \tau τ: θ ( τ + 1 ) ← θ ( τ ) + ρ ( τ ) ( 1 n ∑ i = 1 n ▽ θ L i ( θ ) ∣ θ = θ ( τ ) ) \theta^{(\tau + 1)} \leftarrow \theta^{(\tau)} + \rho(\tau)\left( \frac{1}{n} \sum_{i=1}^n \triangledown_{\theta} L_i(\theta) \mid_{\theta = \theta^{(\tau)}}\right) θ(τ+1)←θ(τ)+ρ(τ)(n1i=1∑n▽θLi(θ)∣θ=θ(τ))
23.5.2 随机梯度下降更新规则
θ ( 0 ) ← 初始向量(随机,零,...) \theta^{(0)} \leftarrow \text{初始向量(随机,零,...)} θ(0)←初始向量(随机,零,...)
对于从 0 到收敛的 τ \tau τ,令 B B B ~ 索引的随机子集 \text{索引的随机子集} 索引的随机子集。 θ ( τ + 1 ) ← θ ( τ ) + ρ ( τ ) ( 1 ∣ B ∣ ∑ i ∈ B ▽ θ L i ( θ ) ∣ θ = θ ( τ ) ) \theta^{(\tau + 1)} \leftarrow \theta^{(\tau)} + \rho(\tau)\left( \frac{1}{|B|} \sum_{i \in B} \triangledown_{\theta} L_i(\theta) \mid_{\theta = \theta^{(\tau)}}\right) θ(τ+1)←θ(τ)+ρ(τ)(∣B∣1i∈B∑▽θLi(θ)∣θ=θ(τ))
二十四、PCA I
原文:PCA I
译者:飞龙
协议:CC BY-NC-SA 4.0
学习成果
-
讨论数据集的维度和降维的策略
-
定义和执行 PCA 的过程
-
理解 PCA 和 SVD 之间的联系
24.1 维度
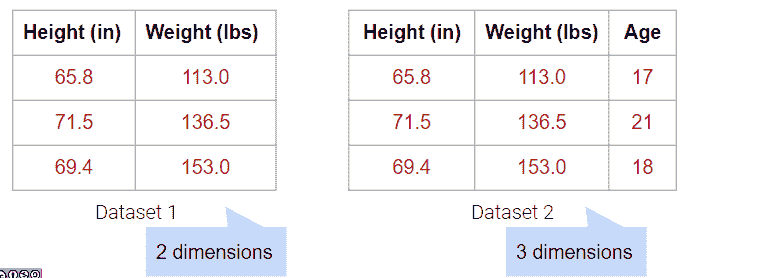
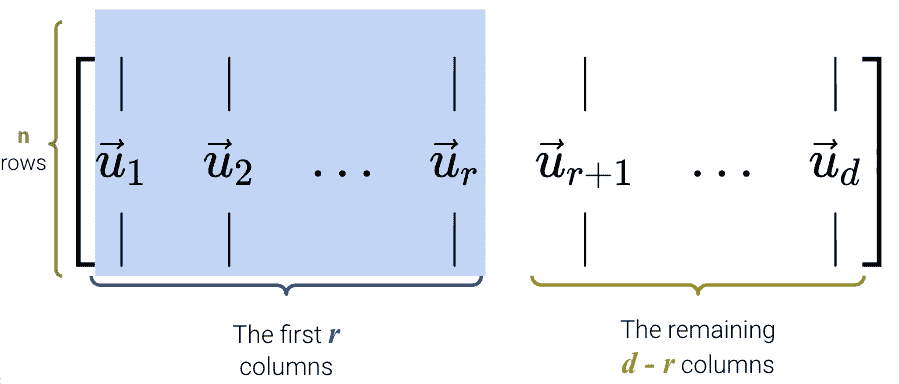
以前,我们一直在处理具有行和列的数据表。这些行和列对应于关于观察的属性。现在,我们必须更清楚地表达我们的措辞,以遵循线性代数的语言。
假设我们有一个数据集:
-
N 个观察(数据点/行)
-
d 个属性(特征/列)
在线性代数中,我们认为数据是向量的集合。向量有一个维度,意味着它们有一些唯一的元素。现在,行和列表示向量写的方向(水平,像一行,或垂直,像一列):
线性代数将我们的数据视为一个矩阵:
-
d 维度中的 N 行向量,或
-
d 列向量在 N 维度
数据的维度是一个复杂的话题。有时,从行/列的数量就可以看出来,但有时却不行。
到目前为止,我们已经使用了像 rugplots 或 scatterplots 这样的可视化来帮助我们识别数据集中的聚类。由于我们人类是 3D 存在,我们无法可视化超过三个维度,但许多数据集具有超过三个特征。为了可视化多维数据,我们可以通过降维来将数据集减少到较低的维度。
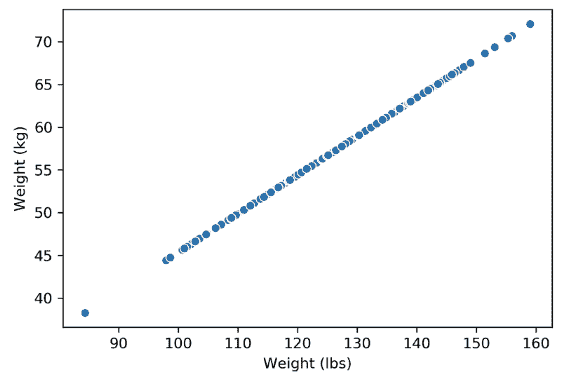
例如,下面的数据集有 4 列,但重量(磅)列实际上只是重量(千克)列的线性变换。因此,没有捕获到新信息,我们的数据集的矩阵具有 3 的(列)秩!尽管有 4 列,我们仍然说这个数据是 3 维的。
将重量列绘制在一起揭示了关键的视觉直觉。虽然两列在视觉上构成了一条线的 2D 空间,但数据并没有偏离那条单一的线。这意味着其中一个重量列是多余的!即使有了覆盖整个 2D 空间的选项,下面的数据也没有。它可能也没有这个维度,这就是为什么我们仍然认为下面的数据不跨越 1 个维度。
当出现异常值时会发生什么?下面,我们在上面的数据集中添加了一个异常值点,这就足以将矩阵的秩从 1 维改变为 2 维。然而,数据仍然是非常明显的 1 维。
因此,降维通常是通过将数据投影到所需维度来实现对原始数据的近似。然而,有许多方法可以将数据集投影到较低的维度。我们如何选择最佳的方法?
一般来说,我们希望找到最好的近似原始数据的投影(右侧的图)。换句话说,我们希望捕获原始数据的最大方差。在下一节中,我们将看到如何计算这一点。
24.2 矩阵作为变换
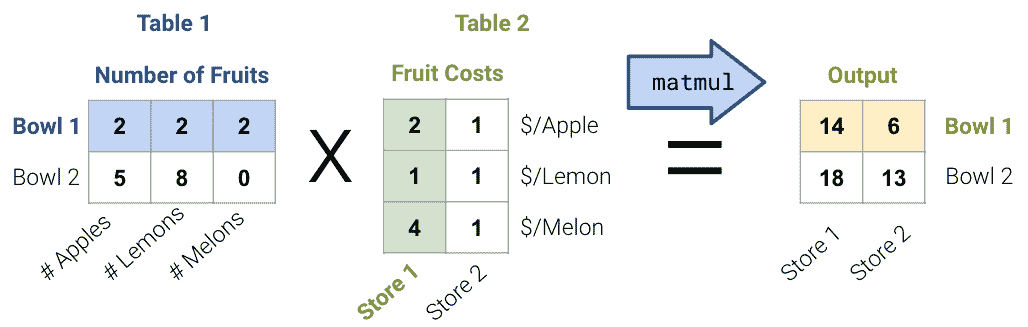
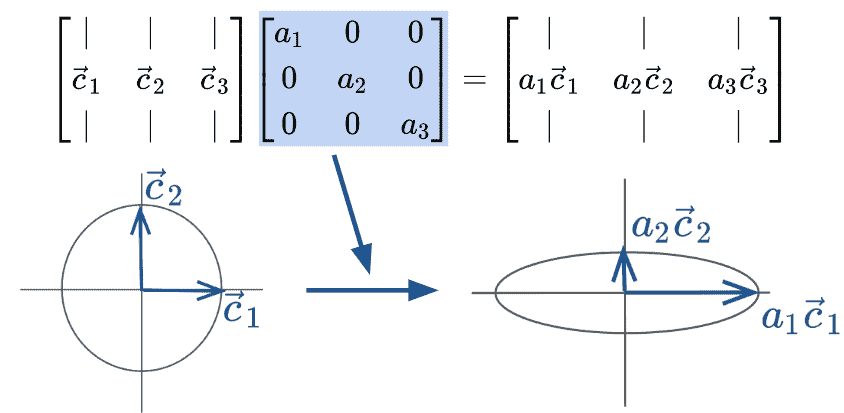
考虑下面的矩阵乘法示例:
-
对于表 1,水果矩阵的每一行代表一碗水果;例如,第一碗/行有 2 个苹果,2 个柠檬和 2 个甜瓜。
-
对于表 2,美元矩阵的每一列代表商店水果的成本;例如,第一个商店/列收取 2 美元一个苹果,1 美元一个柠檬,和 4 美元一个甜瓜。
-
输出是每个商店每碗水果的成本。
一般来说,有两种解释矩阵乘法的方式:
-
行点乘列以获得每个数据点。从这个角度来看,我们对数据执行多个线性操作!
-
列的线性变换!
24.3 主成分分析(PCA)
在 PCA 中,我们的目标是通过线性变换将观察从高维数据转换为低维(通常是 2 维,因为大多数可视化是 2D),换句话说,我们希望找到一个线性变换,创建一个低维表示,尽可能多地捕获原始数据的总方差。
我们经常在数据科学生命周期的探索性数据分析(EDA)阶段进行 PCA,当我们不知道要使用什么模型时。它帮助我们:
-
在高维度中直观地识别相似观察的聚类。
-
如果我们怀疑数据集本质上是低秩的,可以去除不相关的维度。例如,如果列是共线的,有许多属性,但只有少数属性通过线性关联大部分决定其他属性。
-
找到表示复杂事物变化的小基础,例如图像、基因。
-
减少维度以使一些计算更便宜。
24.3.1 PCA 过程(概述)
对矩阵执行 PCA:
-
通过减去每个属性列的平均值来使数据矩阵居中。
-
要找到第 i i i个主成分 v i v_i vi:
-
v v v是一个单位向量,线性组合属性。
-
v v v给出了数据的一维投影。
-
选择 v v v以最小化每个点与其在 v v v上的投影之间的平方距离。
-
选择 v v v,使其与所有先前的主成分正交。
-
第 k k k个主成分捕获了数据矩阵的任何 k k k维降维的最大方差。
然而,在实践中,我们不执行步骤 2 中的程序,因为计算时间太长。相反,我们使用奇异值分解(SVD)来高效地找到所有主成分。
24.4 奇异值分解(SVD)
奇异值分解(SVD)是线性代数中的一个重要概念。由于这门课程要求先修/同步学习线性代数课程(MATH 54, 56 或 EECS 16A),我们假设您已经学过或正在学习线性代数课程,因此我们不会完整地解释 SVD。特别是,我们将讨论:
-
为什么 SVD 是矩形矩阵的有效分解
-
为什么 PCA 是 SVD 的一个应用。
我们不会深入研究 SVD 的理论和细节。相反,我们只会涵盖数据科学解释所需的内容。如果您想了解更多信息,请查看EECS 16B Note 14或EECS 16B Note 15。
[线性代数] 正交性
正交是两个词的组合:正交和正规。
当我们说一个矩阵的列是正交的时,我们说 1. 列之间都是正交的(所有列对的点积为零)2. 所有列都是单位向量(每个列向量的长度为 1)!
正交矩阵有一些重要的性质
-
正交逆:如果一个 m × n m \times n m×n矩阵 Q Q Q具有正交列, Q Q T = I m QQ^T= Iₘ QQT=Im和 Q T Q = I n Q^TQ=Iₙ QTQ=In。
-
坐标旋转:由正交矩阵表示的线性变换通常是旋转(较少是反射)。我们可以想象矩阵的列是原始空间的单位向量将会落在哪里。**[线性代数] 对角矩阵
*对角矩阵**是具有对角轴上非零值的方阵,其他地方都是零。
右乘对角矩阵通过一个常数因子使每列缩放。从几何上看,这种变换可以被视为缩放坐标系。
奇异值分解(SVD)描述了矩阵 X X X的分解成三个矩阵: X = U Σ V T X = U \Sigma V^T X=UΣVT
让我们逐个分解这些术语。
24.4.1 U U U
-
U U U是一个 n × d n \times d n×d的矩阵: U ∈ R n × d U \in \mathbb{R}^{n \times d} U∈Rn×d。
-
它的列是正交的
-
对于所有的 i , j i, j i,j对, u i ˉ T u j ˉ = 0 \bar{u_i}^T\bar{u_j} = 0 uiˉTujˉ=0
-
所有向量 u i ˉ \bar{u_i} uiˉ都是长度为 1 的单位向量。
-
-
U 的列被称为左奇异向量。
-
U U T = I n UU^T = I_n UUT=In和 U T U = I d U^TU = I_d UTU=Id。
-
我们可以把 U U U看作是一个旋转。
24.4.2 Σ \Sigma Σ
-
Σ \Sigma Σ是一个 d × d d \times d d×d的矩阵: Σ ∈ R d × d \Sigma \in \mathbb{R}^{d \times d} Σ∈Rd×d。
-
矩阵的大部分是零
-
它有 r r r个非零奇异值, r r r是 X X X的秩
-
对角值(奇异值 σ 1 , σ 2 , . . . σ r \sigma_1, \sigma_2, ... \sigma_r σ1,σ2,...σr)按从大到小的顺序排列 σ 1 > σ 2 > . . . > σ r \sigma_1 > \sigma_2 > ... > \sigma_r σ1>σ2>...>σr
-
我们可以把 Σ \Sigma Σ看作是缩放。
24.4.3 V T V^T VT
-
V T V^T VT是一个 d × d d \times d d×d的矩阵: V ∈ R d × d V \in \mathbb{R}^{d \times d} V∈Rd×d。
-
V V V的列是正交的,所以 V T V^T VT的行也是正交的
-
V V V的列被称为右奇异向量。
-
V V T = V T V = I d VV^T = V^TV = I_d VVT=VTV=Id
-
我们可以把 V V V看作是一个旋转。
24.4.4 SVD:几何视角
我们已经看到 U U U和 V V V代表旋转, Σ \Sigma Σ代表缩放。因此,SVD 表示任何矩阵都可以分解为一个旋转,然后一个缩放,再一个旋转。
24.4.5 NumPy中的 SVD
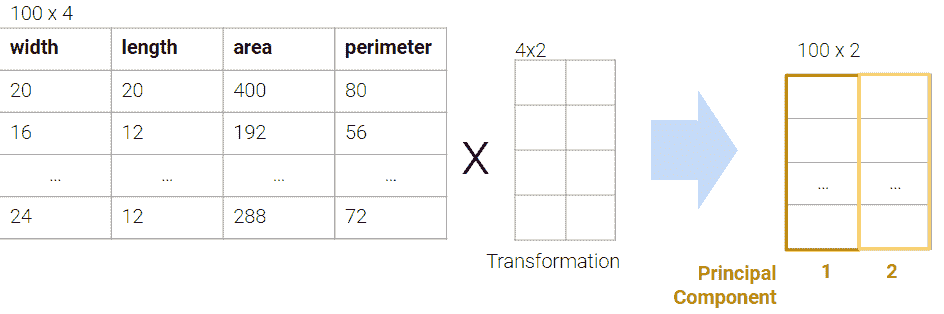
对于这个演示,我们将继续使用之前的矩形数据集,其中 n = 100 n=100 n=100行, d = 4 d=4 d=4列。
代码
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(23) #kallisti
plt.rcParams['figure.figsize'] = (4, 4)
plt.rcParams['figure.dpi'] = 150
sns.set()
rectangle = pd.read_csv("data/rectangle_data.csv")
rectangle.head(5)
| Width | Height | Area | Perimeter | |
|---|---|---|---|---|
| 0 | 8 | 6 | 48 | 28 |
| 1 | 2 | 4 | 8 | 12 |
| 2 | 1 | 3 | 3 | 8 |
| 3 | 9 | 3 | 27 | 24 |
| 4 | 9 | 8 | 72 | 34 |
在NumPy中,SVD 算法已经编写好,可以用np.linalg.svd来调用(文档)。有多个版本的 SVD;要获得我们将遵循的版本,需要将full_matrices参数设置为False。
U, S, Vt = np.linalg.svd(rectangle, full_matrices = False)
首先,让我们检查U。正如我们所看到的,它的维度是 n × d n \times d n×d。
U.shape
(100, 4)
下面显示了U的前 5 行。
pd.DataFrame(U).head(5)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | -0.155151 | 0.064830 | -0.029935 | 0.638430 |
| 1 | -0.038370 | -0.089155 | 0.062019 | -0.351010 |
| 2 | -0.020357 | -0.081138 | 0.058997 | 0.018831 |
| 3 | -0.101519 | -0.076203 | -0.148160 | -0.199067 |
| 4 | -0.218973 | 0.206423 | 0.007274 | -0.079833 |
在NumPy中, Σ \Sigma Σ有点不同。因为对角矩阵 Σ \Sigma Σ中唯一有用的值是对角轴上的奇异值,所以只返回这些值,并将它们存储在一个数组中。
我们的rectangle_data的秩是 3 3 3,所以我们应该有 3 个非零奇异值,按从大到小的顺序排列。
S
array([3.62932568e+02, 6.29904732e+01, 2.56544651e+01, 2.56949990e-15])
看起来我们有 4 个非零值而不是 3 个,但请注意最后一个值非常小( 1 0 − 15 10^{-15} 10−15),实际上几乎等于 0 0 0。因此,我们可以四舍五入这些值,得到 3 个奇异值。
np.round(S)
array([363., 63., 26., 0.])
要以矩阵格式获得S,我们使用np.diag。
Sm = np.diag(S)
Sm
array([[3.62932568e+02, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[0.00000000e+00, 6.29904732e+01, 0.00000000e+00, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 2.56544651e+01, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 2.56949990e-15]])
最后,我们可以看到Vt确实是一个 d × d d \times d d×d的矩阵。
Vt.shape
(4, 4)
pd.DataFrame(Vt)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | -0.146436 | -0.129942 | -8.100201e-01 | -0.552756 |
| 1 | -0.192736 | -0.189128 | 5.863482e-01 | -0.763727 |
| 2 | -0.704957 | 0.709155 | 7.951614e-03 | 0.008396 |
| 3 | -0.666667 | -0.666667 | -5.257886e-17 | 0.333333 |
要检查这个 SVD 是否是一个有效的分解,我们可以反向进行,并看它是否与我们原来的表匹配(它确实匹配,耶!)。
pd.DataFrame(U @ Sm @ Vt).head(5)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 8.0 | 6.0 | 48.0 | 28.0 |
| 1 | 2.0 | 4.0 | 8.0 | 12.0 |
| 2 | 1.0 | 3.0 | 3.0 | 8.0 |
| 3 | 9.0 | 3.0 | 27.0 | 24.0 |
| 4 | 9.0 | 8.0 | 72.0 | 34.0 |
24.5 PCA with SVD
主成分分析(PCA)和奇异值分解(SVD)很容易混淆,尤其是当你不得不记住这么多首字母缩略词时。这里是一个快速总结:
-
SVD: 一个线性代数算法,将矩阵分成 3 个组成部分。
-
PCA: 一种用于降维的数据科学程序,使用 SVD 作为其中一步。
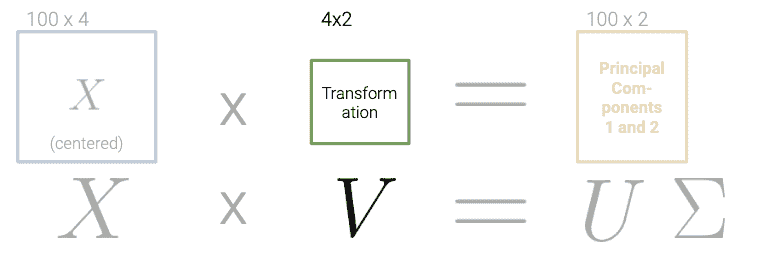
为了从一个 n × d n \times d n×d矩阵 X X X中获得前 k k k个主成分,我们需要:
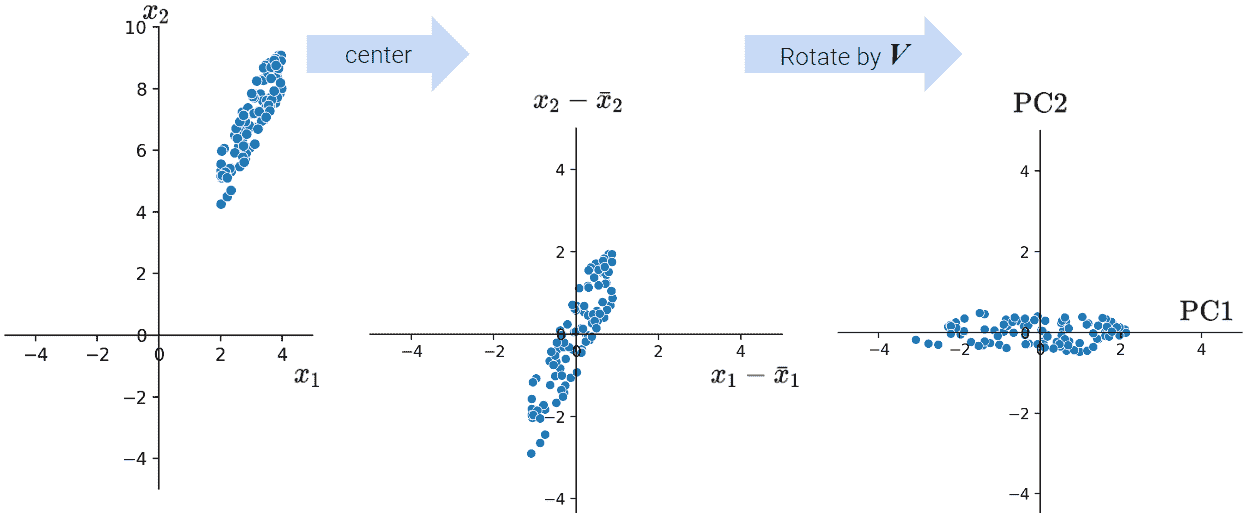
- 通过从每一列中减去均值来对 X X X进行中心化。请注意,我们指定
axis=0,以便按列计算均值。
centered_df = rectangle - np.mean(rectangle, axis = 0)
centered_df.head(5)
| Width | Height | Area | Perimeter | |
|---|---|---|---|---|
| 0 | 2.97 | 1.35 | 24.78 | 8.64 |
| 1 | -3.03 | -0.65 | -15.22 | -7.36 |
| 2 | -4.03 | -1.65 | -20.22 | -11.36 |
| 3 | 3.97 | -1.65 | 3.78 | 4.64 |
| 4 | 3.97 | 3.35 | 48.78 | 14.64 |
- 获得中心化 X X X的奇异值分解: U U U, Σ Σ Σ 和 V T V^T VT
U, S, Vt = np.linalg.svd(centered_df, full_matrices = False)
Sm = pd.DataFrame(np.diag(np.round(S, 1)))
- 将 U Σ UΣ UΣ或 X V XV XV相乘。从数学上讲,这些给出了相同的结果,但在计算上,浮点近似导致非常小的值的略有不同的数字(查看下面单元格中最右边的列)。
# UΣ
pd.DataFrame(U @ np.diag(S)).head(5)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | -26.432217 | 0.162686 | 0.807998 | -1.447811e-15 |
| 1 | 17.045285 | -2.181451 | 0.347732 | 3.893239e-15 |
| 2 | 23.245695 | -3.538040 | 1.995334 | -4.901321e-16 |
| 3 | -5.383546 | 5.025395 | 0.253448 | -3.544636e-16 |
| 4 | -51.085217 | -2.586948 | 2.099919 | -4.133102e-16 |
# XV
pd.DataFrame(centered_df @ Vt.T).head(5)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | -26.432217 | 0.162686 | 0.807998 | -1.539509e-15 |
| 1 | 17.045285 | -2.181451 | 0.347732 | -2.072416e-16 |
| 2 | 23.245695 | -3.538040 | 1.995334 | 4.588922e-16 |
| 3 | -5.383546 | 5.025395 | 0.253448 | -4.292862e-16 |
| 4 | -51.085217 | -2.586948 | 2.099919 | -1.650532e-15 |
- 取 U Σ UΣ UΣ(或 X V XV XV)的前 k k k列。这些是 X X X的前 k k k个主成分。
two_PCs = (U @ np.diag(S))[:, :2] # using UΣ
two_PCs = (centered_df @ Vt.T).iloc[:, :2] # using XV
pd.DataFrame(two_PCs).head()
| 0 | 1 | |
|---|---|---|
| 0 | -26.432217 | 0.162686 |
| 1 | 17.045285 | -2.181451 |
| 2 | 23.245695 | -3.538040 |
| 3 | -5.383546 | 5.025395 |
| 4 | -51.085217 | -2.586948 |
24.6 (奖金) PCA vs. 回归
24.6.1 回归:最小化水平/垂直误差
假设我们知道某个国家的儿童死亡率。线性回归试图从死亡率预测生育率;例如,如果死亡率为 6,我们可能猜测生育率接近 4。回归线告诉我们,通过最小化均方根误差[见垂直红线,仅显示部分],给出了所有可能死亡率值的生育率的“最佳”预测。
我们也可以在相反的方向进行回归,也就是说,给定生育率,我们试图预测死亡率。在这种情况下,我们得到了一条不同的回归线,它最小化了水平线的均方根长度。
24.6.2 SVD:最小化垂直误差
秩 1 近似接近但不同于死亡率回归线。我们的秩 1 近似不是最小化水平或垂直误差,而是最小化垂直到我们投影的子空间上的误差。也就是说,SVD 找到了这样一条线,如果我们将我们的数据投影到该线上,投影与我们的原始数据之间的误差将被最小化。秩 1 近似与生育率的相似性只是一个巧合。从我们的身体测量数据集中查看脂肪和二头肌大小,我们看到我们正在投影的一维子空间位于两条回归线之间。
24.6.3 超过 1D 和 2D
在更高的维度中,主成分背后的思想是一样的!假设我们有 30 维数据,并决定使用前 5 个主成分。我们的过程最小化了原始 30 维数据与该 30 维数据投影到“最佳”5 维子空间之间的误差。有关更多详细信息,请参见CS189。
24.7(奖金)自动因子分解
要记住的一个关键事实是,分解并不是任意的。矩阵的秩限制了如果我们想要完美重现我们的矩阵,我们的内部维度可以有多小。这个证明超出了范围。
即使我们知道我们必须使用 R 的内部维度来分解我们的矩阵,仍然留下了一个要遍历的大空间解决方案。如果我们有一个自动将秩为 R 的矩阵因子分解为具有一些变换矩阵的 R 维表示的过程呢?
-
低维表示避免了冗余特征。
-
想象一个 1000 维的数据集:如果秩只有 5,那么在这个神秘过程之后进行 EDA 会容易得多。
如果我们想要一个 2D 表示呢?将所有相关数据压缩到尽可能少的维度上以便有效地绘制它是有价值的。一些 2D 矩阵比其他矩阵产生更好的近似。我们能做得有多好呢?
24.8(奖金)组分得分的证明
定义组分得分的证明超出了本课程的范围,但为了您的方便,下面包括了它。
设置:考虑设计矩阵 X ∈ R n × d X \in \mathbb{R}^{n \times d} X∈Rn×d,其中第 j j j列(对应于第 j j j个特征)是 x j ∈ R n x_j \in \mathbb{R}^n xj∈Rn,第 i i i行,第 j j j列的元素是 x i j x_{ij} xij。此外,将 X ~ \tilde{X} X~定义为居中设计矩阵。第 j j j列是 x ~ j ∈ R n \tilde{x}_j \in \mathbb{R}^n x~j∈Rn,第 i i i行,第 j j j列的元素是 x ~ i j = x i j − x j ˉ \tilde{x}_{ij} = x_{ij} - \bar{x_j} x~ij=xij−xjˉ,其中 x j ˉ \bar{x_j} xjˉ是原始 X X X的 x j x_j xj列向量的均值。
方差:构造协方差矩阵: 1 n X ~ T X ~ ∈ R d × d \frac{1}{n} \tilde{X}^T \tilde{X} \in \mathbb{R}^{d \times d} n1X~TX~∈Rd×d。对角线上的第 j j j个元素是原始设计矩阵 X X X的第 j j j列的方差:
( 1 n X ~ T X ~ ) j j = 1 n x ~ j T x ~ j = 1 n ∑ i = i n ( x ~ i j ) 2 = 1 n ∑ i = i n ( x i j − x j ˉ ) 2 \left( \frac{1}{n} \tilde{X}^T \tilde{X} \right)_{jj} = \frac{1}{n} \tilde{x}_j ^T \tilde{x}_j = \frac{1}{n} \sum_{i=i}^n (\tilde{x}_{ij} )^2 = \frac{1}{n} \sum_{i=i}^n (x_{ij} - \bar{x_j})^2 (n1X~TX~)jj=n1x~jTx~j=n1i=i∑n(x~ij)2=n1i=i∑n(xij−xjˉ)2
SVD:假设居中设计矩阵 X ~ \tilde{X} X~的奇异值分解为 X ~ = U Σ V T \tilde{X} = U \Sigma V^T X~=UΣVT,其中 U ∈ R n × d U \in \mathbb{R}^{n \times d} U∈Rn×d和 V ∈ R d × d V \in \mathbb{R}^{d \times d} V∈Rd×d是具有正交列的矩阵, Σ ∈ R d × d \Sigma \in \mathbb{R}^{d \times d} Σ∈Rd×d是具有 X ~ \tilde{X} X~的奇异值的对角线矩阵。
最后一行定义了第 j j j个组分得分。
二十五、PCA II
原文:PCA II
译者:飞龙
协议:CC BY-NC-SA 4.0
学习成果
-
深入理解如何解释主成分分析(PCA)。
-
看看 PCA 在一些现实世界的应用。
25.1 PCA 回顾
25.1.1 使用 SVD 的 PCA
在找到 X X X的 SVD 之后:
我们可以推导出数据的主成分。具体来说, V T V^{T} VT的前 n n n行是 n n n个主成分的方向。
25.1.2 V 的列是方向
V V V的每一列元素( V T V^{T} VT的每一行)将原始特征向量旋转成一个主成分。
V 的第一列表示每个特征对第一个主成分的贡献(例如正面、负面等)。
这种解释也让我们理解:
-
主成分都是正交的,因为 U 的列是标准正交的。
-
主成分是轴对齐的。也就是说,如果你在二维平面上绘制两个主成分,一个会在 x 轴上,另一个会在 y 轴上。
-
主成分是我们数据 X 中列的线性组合
25.1.3 使用主成分
让我们总结通过 SVD 获取主成分的步骤:
-
通过减去每个属性列的平均值来使数据矩阵居中。
-
要找到 k k k个主成分:
-
计算数据矩阵的 SVD( X = U Σ V T X = U{\Sigma}V^{T} X=UΣVT)
-
U Σ U{\Sigma} UΣ的前 k k k列(或者等价地, X V XV XV)包含了 X X X的 k k k个主成分。
-
25.2 数据方差和居中
我们定义数据矩阵的总方差为属性方差的总和。主成分是一个低维表示,尽可能多地捕捉原始数据的总方差。形式上,第 i i i个奇异值告诉我们成分得分,即第 i i i个主成分捕捉了多少数据方差。假设数据点的数量是 n n n:
i-th component score = ( i-th singular value 2 ) n \text{i-th component score} = \frac{(\text{i-th singular value}^2)}{n} i-th component score=n(i-th singular value2)
将成分得分相加等同于计算总方差如果我们对数据进行了居中。
数据居中:PCA 有一个数据居中的步骤,它在任何奇异值分解之前进行,如果实施了,就会定义上面的成分得分。
如果你想深入了解 PCA,Steve Brunton 的 SVD 视频系列是一个很好的资源。
25.3 解释 PCA
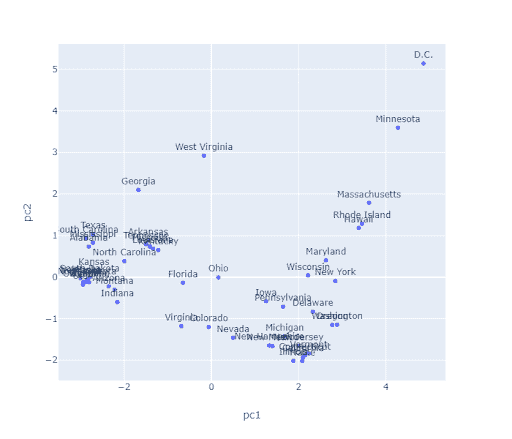
25.3.1 案例研究:众议院投票
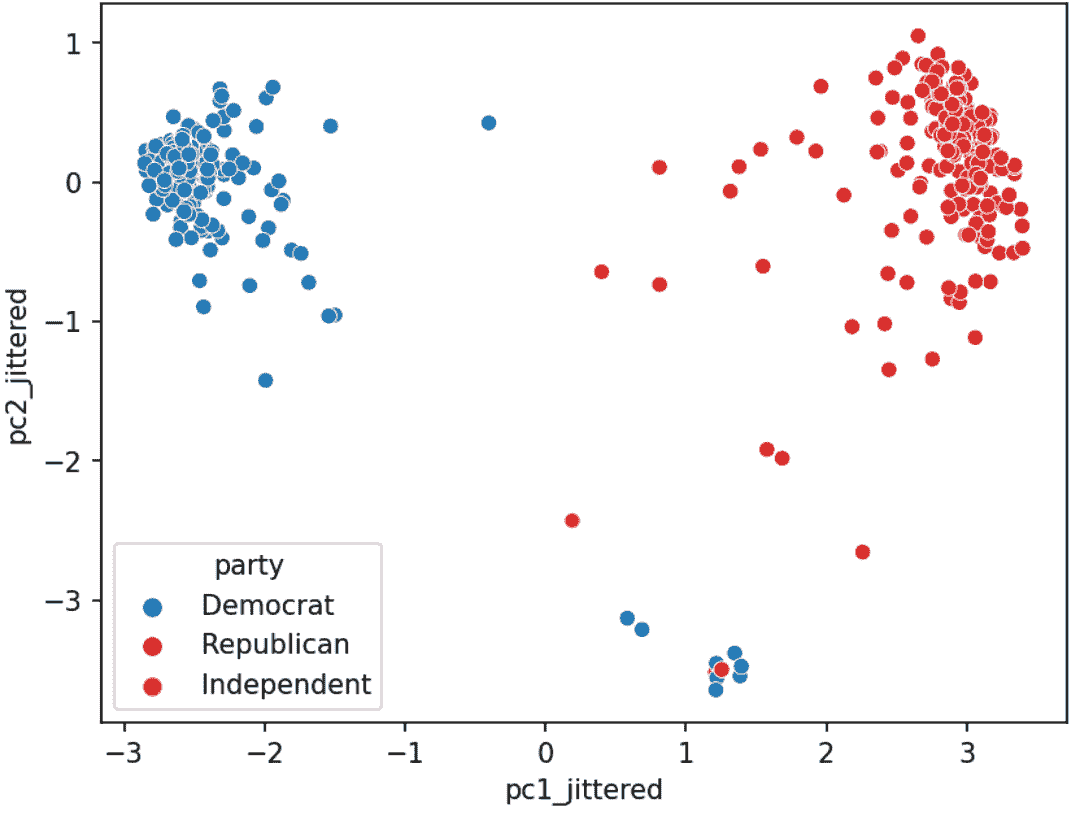
让我们来看看众议院(第 116 届国会,第 1 届会议)在 2019 年 9 月投票的情况。
具体来说,我们将查看点名投票的记录。来自美国参议院(链接):点名投票发生在代表或参议员投票“赞成”或“反对”时,以便记录每一方投票的成员的名字。口头表决是指那些赞成或反对某项措施的人分别说“赞成”或“反对”,而不记录每一方投票的成员的名字或计数。
立法者的点名投票是否与他们的政党有关?
请访问此链接查看完整的 Jupyter 笔记本演示。
正如演示所示,PCA 的主要目标是通过线性变换将高维数据的观测值转换为低维数据。
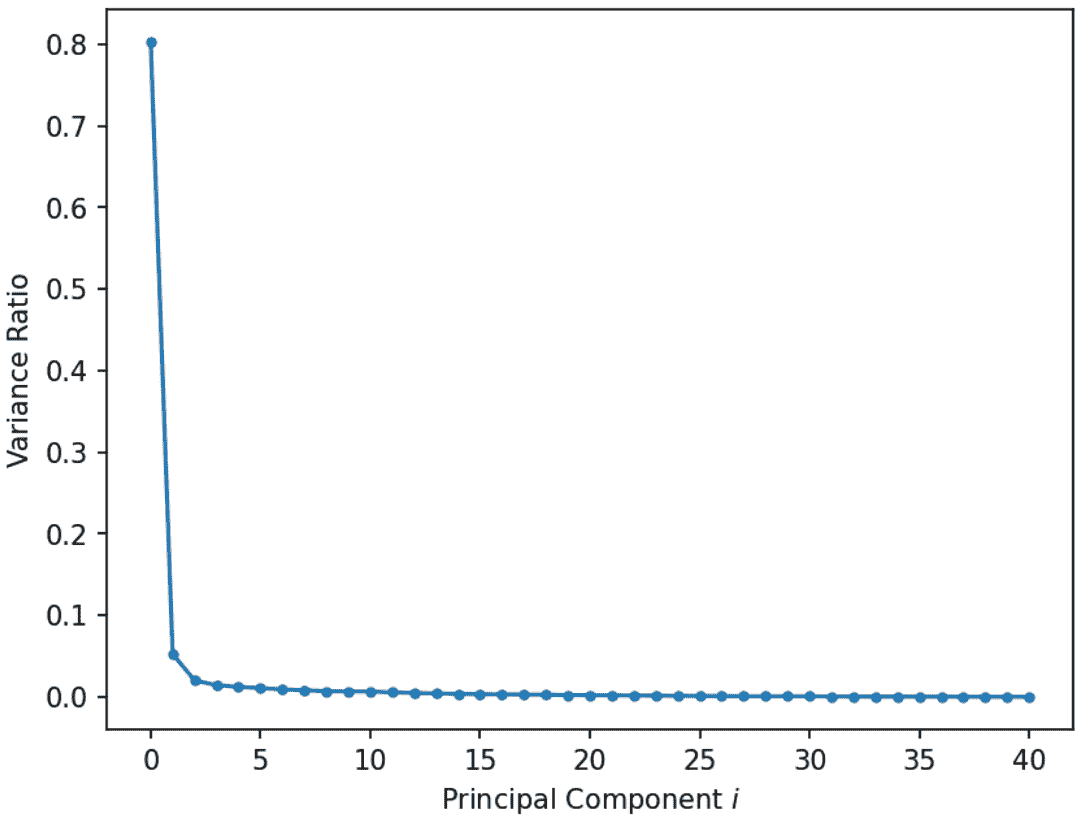
PCA 的一个相关目标是将数据的低维表示捕捉原始数据的变异性。例如,如果前两个奇异值很大,而其他奇异值相对较小,那么两个维度可能足以描述大部分区分观测之间的差异。然而,如果情况并非如此,那么 PCA 散点图可能遗漏了大量信息。
我们可以使用以下公式来量化每个主成分对总方差的贡献:
成分得分 = σ i 2 N \text{成分得分} = \frac{\sigma_i^{2}}{N} 成分得分=Nσi2
总方差 = 所有成分得分之和 = ∑ i = 1 k σ i 2 N \text{总方差} = \text{所有成分得分之和} = \sum_{i=1}^k \frac{\sigma_i^{2}}{N} 总方差=所有成分得分之和=i=1∑kNσi2
主成分 i 的方差比率 = 主成分得分 i 总方差 = σ i 2 / N ∑ i = 1 k σ i 2 / N \text{主成分 i 的方差比率} = \frac{\text{主成分得分 i}}{\text{总方差}} = \frac{\sigma_i^{2} / N}{\sum_{i=1}^k \sigma_i^{2} / N} 主成分 i 的方差比率=总方差主成分得分 i=∑i=1kσi2/Nσi2/N
在 Python 中,假设您有一个由np.linalg.svd返回的奇异值s的一维NumPy数组,您可以使用s**2 / sum(s**2)计算方差比率的列表。
25.3.2 PCA 图
我们经常使用散点图绘制前两个主成分,其中 PC1 在 x x x-轴上,PC2 在 y y y-轴上。这通常被称为 PCA 图。
如果前两个奇异值很大,而其他奇异值很小,那么两个维度足以描述大部分区分观测之间的差异。如果不是这样,那么 PCA 图遗漏了大量信息。
PCA 图帮助我们评估数据点之间的相似性以及数据集中是否存在任何聚类。例如,在之前的案例研究中,我们可以创建以下 PCA 图:
25.3.3 屏幕图
屏幕图显示了每个主成分捕获的方差比率,首先是最大的方差比率。它们帮助我们直观地确定描述数据所需的维度数量。在图中大幅下降后的区域中的奇异值对应于不需要描述数据的主成分,因为它们解释了数据总方差的相对较低比例。例如,在下面的图中,我们可以使用刚才描述的“拐点法”来确定前 2 个 PCs 捕获了大部分信息。
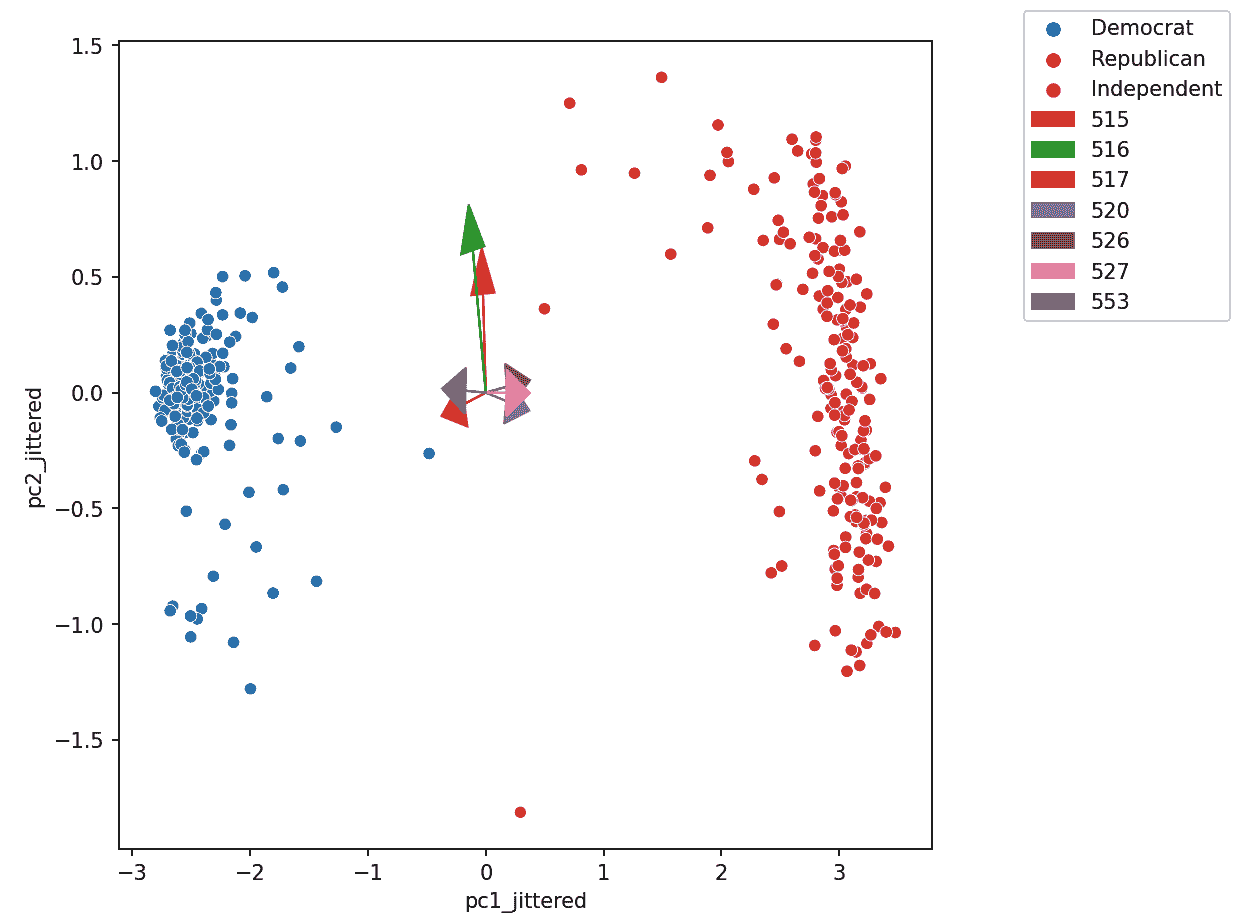
25.3.4 双标图
双标图将方向叠加到 PC2 vs PC1 的图上,其中向量 j j j对应于特征 j j j的方向(例如 v 1 j , v 2 j v_{1j}, v_{2j} v1j,v2j)。有几种方法可以缩放双标图向量-在本课程中,我们绘制方向本身。对于其他缩放,可以导致更可解释的方向/载荷,请参阅SAS 双标图
通过双标图,我们可以解释特征如何与所示的主成分相关联:正相关、负相关或几乎没有相关。
箭头的方向是( v 1 v_1 v1, v 2 v_2 v2),其中 v 1 v_1 v1和 v 2 v_2 v2是特定特征列对 PC1 和 PC2 的贡献, v 1 v_1 v1和 v 2 v_2 v2分别是 V V V的第一列和第二列的元素(即 V T V^T VT的前两行)。
假设我们正在考虑特征 3,并且说这是标记为“520”的紫色箭头(指向右下角)。
-
v 1 v_1 v1和 v 2 v_2 v2是 V V V中相应列的第三个元素。它们是特征 3 的列向量在线性变换到 PC1 和 PC2 时的比例。
-
在这里,我们可以推断 v 1 v_1 v1(在 x x x/PC1 方向上)是正的,这意味着特征 3 的线性增加将对应于 PC1 的线性增加,这意味着特征 3 和 PC1 呈正相关。
-
v 2 v_2 v2(在 y y y/pc2 方向)为负,意味着特征 3 的线性增加将导致 PC2 的线性减少,这意味着特征 3 和 PC2 呈负相关。
25.4 PCA 的应用
25.4.1 生物学中的 PCA
PCA 通常用于生物医学背景中,其中有许多命名变量!
-
对数据进行聚类(论文 1,论文 2)
-
识别相关变量(解释 V T V^{T} VT 的行作为线性系数)(论文 3)。使用双标图。
25.4.2 为什么执行 PCA
我们经常在数据科学生命周期的探索性数据分析(EDA)阶段执行 PCA(如果我们已经知道要建模什么,我们可能不需要 PCA);它帮助我们:
-
在高维度中直观地识别相似观察的聚类。
-
如果怀疑数据集本质上是低秩的,则移除不相关的维度。例如,如果列是共线的:属性很多,但只有少数属性通过线性关联决定了其余属性。
-
寻找表示复杂事物变化的小基础,例如图像、基因。
-
减少维度以使某些计算更便宜。
25.4.3 图像分类
在机器学习中,PCA 经常用作在训练监督模型之前的预处理步骤。
查看以下演示以了解 PCA 如何有助于基于 MNIST-Fashion 数据集构建图像分类模型。
演示显示了我们如何在数据科学生命周期的探索性数据分析阶段使用 PCA 来:- 在高维度中直观地识别相似观察的聚类。- 寻找表示复杂事物变化的小基础。- 减少维度以使某些计算更便宜。
25.4.4 为什么先 PCA,然后建模?
-
降低维度,使我们能够加快训练速度并减少特征数量等。
-
避免新特征中的多重共线性(即主成分)
二十六、聚类
原文:Clustering
译者:飞龙
协议:CC BY-NC-SA 4.0
学习成果
-
聚类介绍
-
评估聚类方法的分类法
-
K 均值聚类
-
没有明确损失函数的聚类:最小化惯性
-
层次凝聚聚类
-
选择 K:一个超参数
上次,我们通过讨论主成分分析(PCA)开始了我们对无监督学习的探讨。
在本讲座中,我们将探讨另一个非常流行的无监督学习概念:聚类。聚类允许我们在没有给出“类”或每个点明确来自何处的标签的情况下将相似的数据点“分组”在一起。我们将讨论两种聚类算法:K 均值聚类和层次凝聚聚类,并且我们将检查每种算法的假设、优势和局限性。
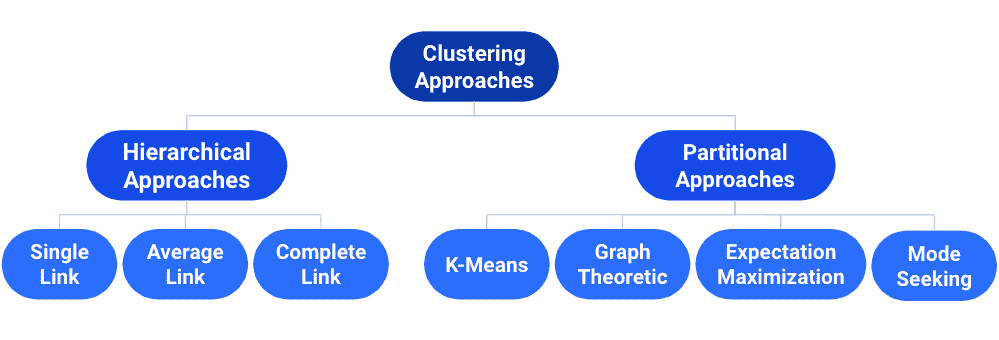
26.1 回顾:机器学习分类法
26.1.1 监督学习
在“监督学习”中,我们的目标是创建一个将输入映射到输出的函数。每个模型都是从示例输入/输出对(训练集)中学习的,使用输入/输出对进行验证,并最终在更多的输入/输出对上进行测试。每对由以下组成:
-
输入向量
-
输出值(标签)
在回归中,我们的输出值是定量的,在分类中,我们的输出值是分类的。
ML 分类法
26.1.2 无监督学习
在无监督学习中,我们的目标是识别无标签数据中的模式。在这种类型的学习中,我们没有输入/输出对。有时我们可能有标签,但选择忽略它们(例如在标记数据上进行 PCA)。相反,我们更感兴趣的是我们所拥有的数据的固有结构,而不是仅仅使用该数据的结构来预测标签。例如,如果我们对降维感兴趣,我们可以使用 PCA 将我们的数据降低到较低的维度。
现在让我们考虑一个新问题:聚类。
26.1.3 聚类示例
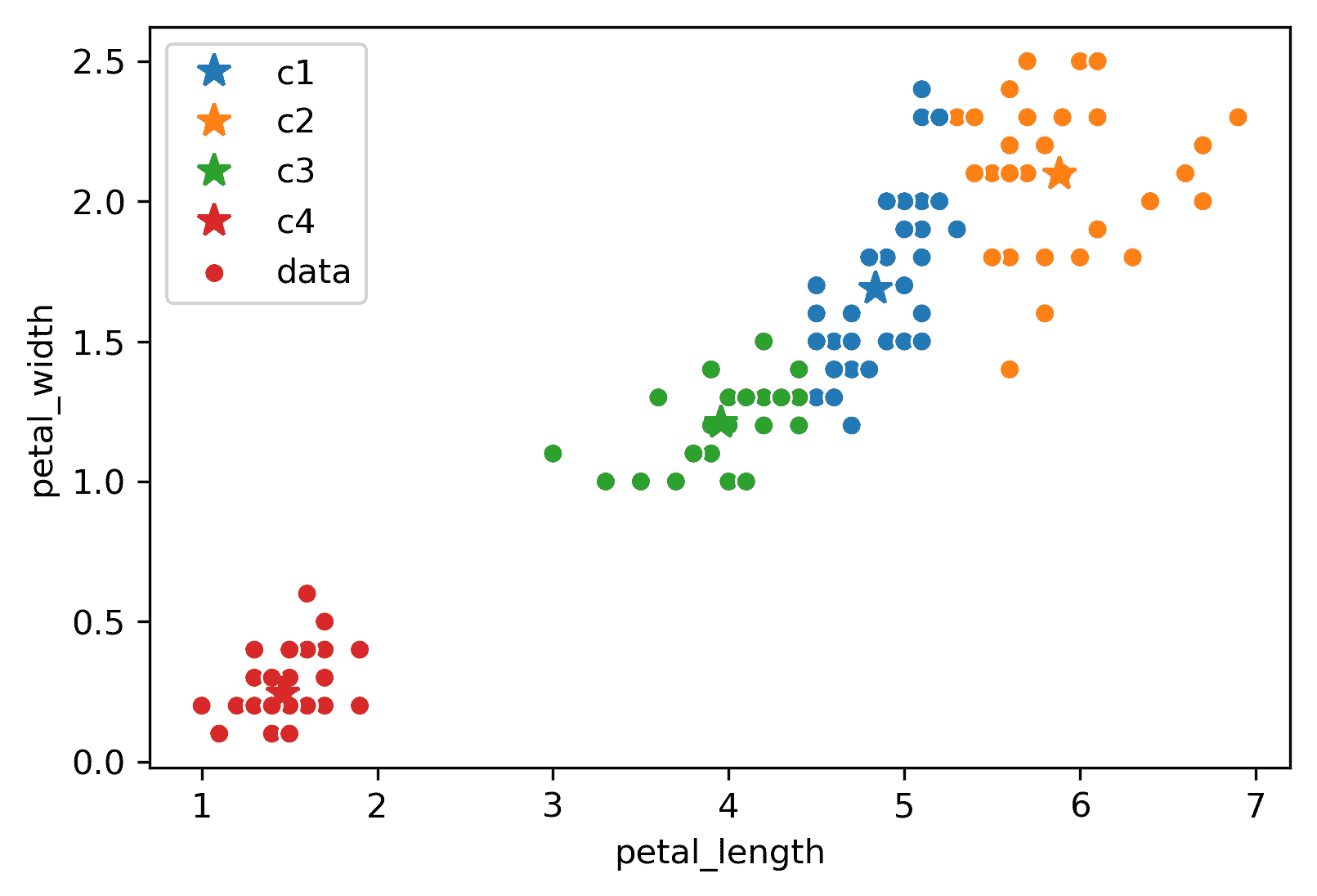
26.1.3.1 示例 1
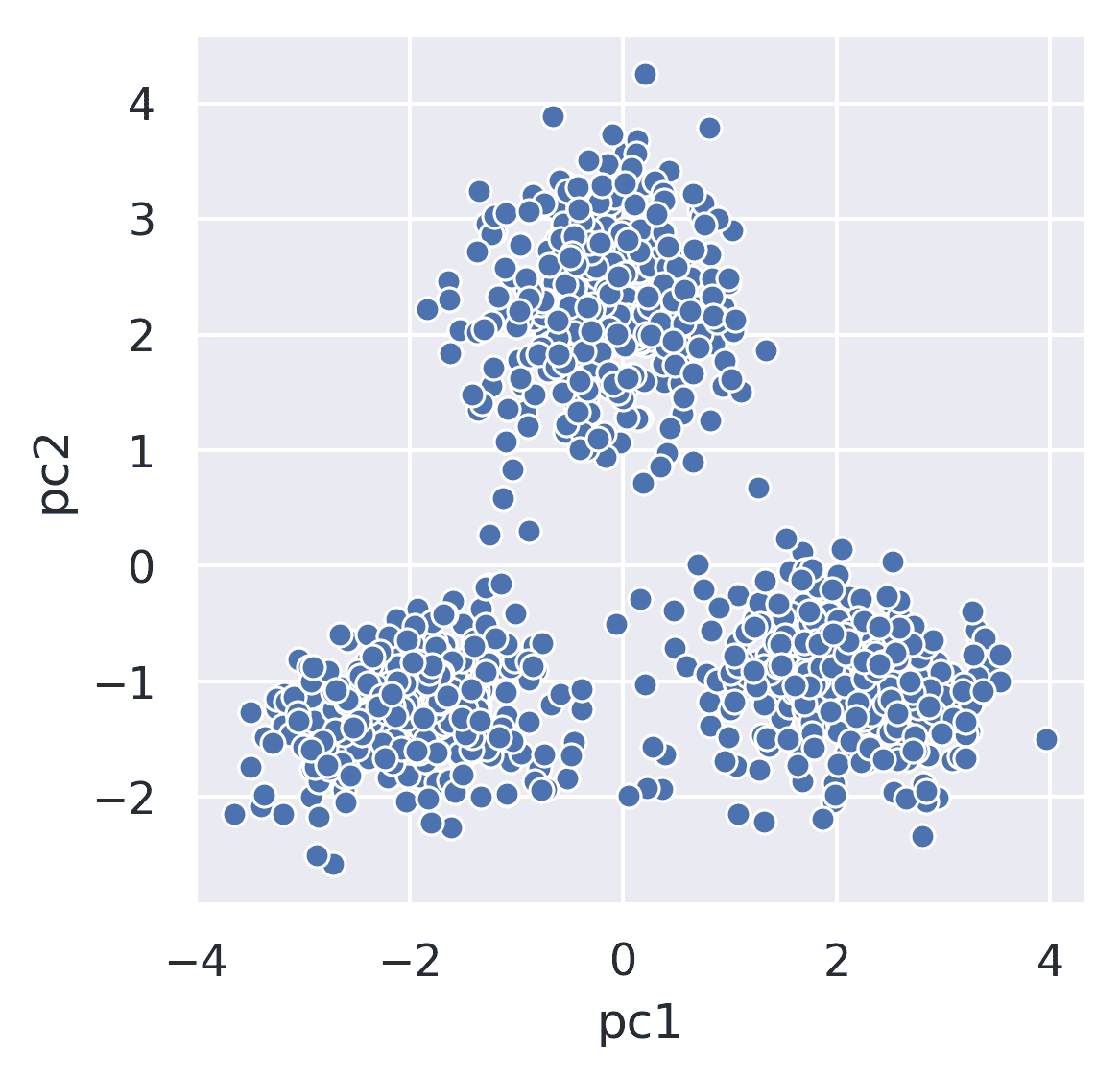
考虑一下 2019 年秋季期中考试 2 的图。原始数据集有 8 个维度,但我们已经使用 PCA 将我们的数据减少到 2 个维度。
每个点表示游客在 8 个不同动物园展品上花费的时间的第一和第二主成分。从视觉和直觉上,我们可能会猜测这些数据属于 3 个组:每个集群一个。现在聚类的目标是将每个点(在 2 维 PCA 表示中)分配到一个集群中。
这是一个无监督的任务,因为:
-
我们没有每个访客的标签。
-
希望推断出模式,即使没有标签。
26.1.3.2 示例 2:Netflix
现在假设你是 Netflix,正在查看有关客户观看习惯的信息。聚类在这里很有用。我们可以将每个人或节目分配到一个“集群”。(注意:虽然我们不能确定 Netflix 是否实际使用 ML 聚类来识别这些类别,但原则上他们可以这样做。)
请记住,对于聚类,我们不需要提前定义聚类。这标志着聚类和分类之间的一个关键区别,而在分类中,我们必须提前决定标签,而聚类会自动发现组。
26.1.3.3 示例 3:教育
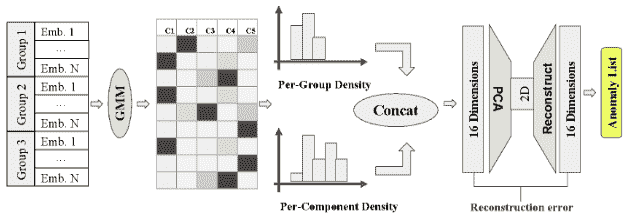
假设我们正在处理学生生成的材料,并将其传递到 S-BERT 模块以提取句子嵌入。从集群中提取特征:
-
检测组活动中的异常
-
预测组的中位数测验成绩
在这里,我们可以看到异常检测模块的大纲。它包括:
-
S-BERT 特征提取
-
主题提取
-
特征提取
-
16D → \rightarrow → 2D PCA 降维和 2D → \rightarrow → 16D 重构
-
基于重构误差的异常检测
更仔细地观察我们的聚类,我们可以更好地理解中心所代表的不同组件。下面我们有两个例子。
请注意,此示例的详细信息不在范围内。
26.1.3.4 例 4:逆向工程生物学
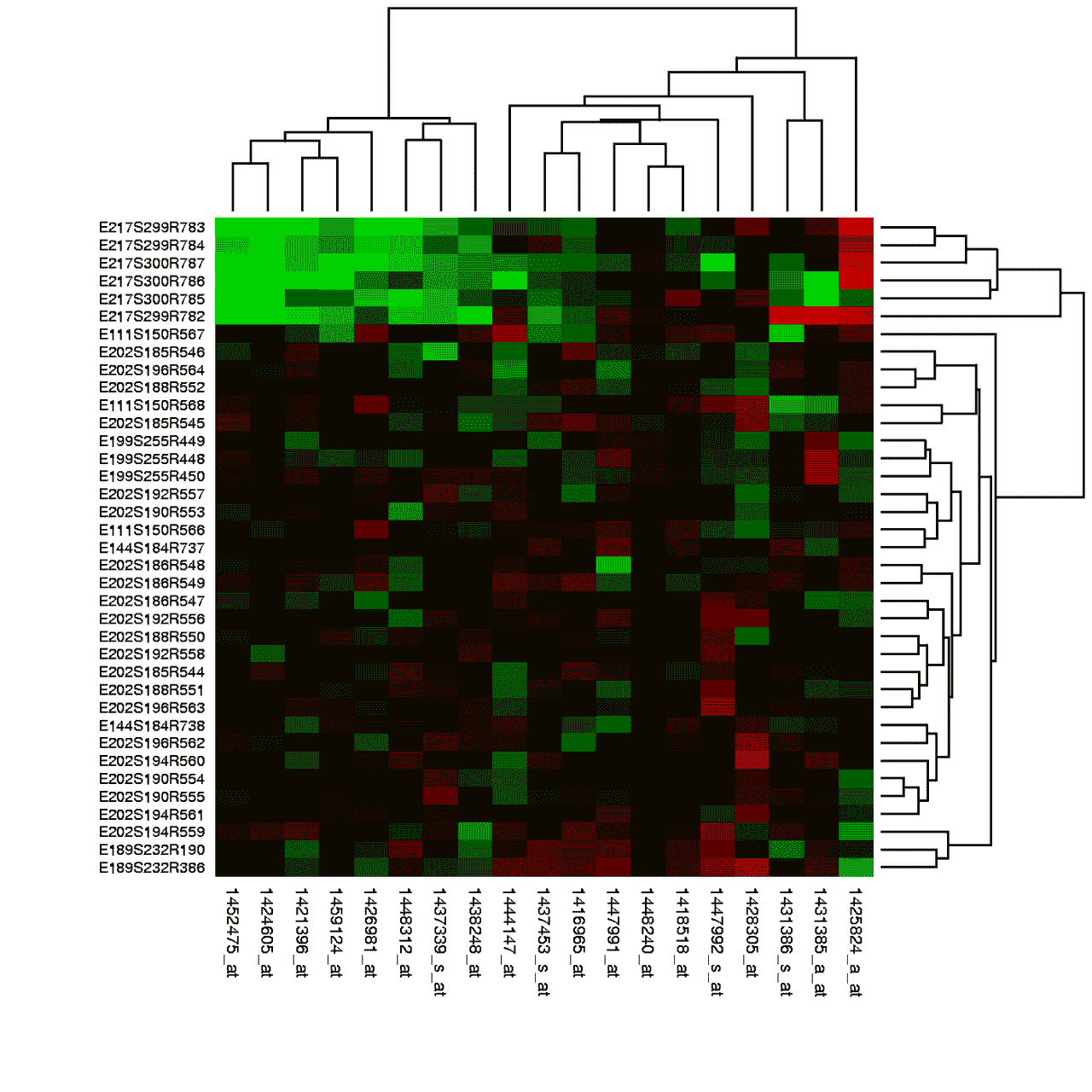
现在,考虑下面的图:
这个图的行是条件(例如一个行可能是:“在细胞上倒酸”),列是基因。绿色表示基因“关闭”(红色表示基因“开启”)。例如,图的左上角的~9 个基因都被顶部的 6 个实验(行)关闭。
在聚类的视角下,我们可能对基于对某些实验的反应(开/关)相似的观察结果进行聚类感兴趣。
例如,这是我们在聚类之前和之后的数据。
注意:如果你无法通过眼睛区分红色和绿色,我很抱歉!历史可视化并不总是最好的。
26.2 聚类方法的分类
有许多类型的聚类算法,它们都有优势、固有的弱点和不同的用例。我们首先将专注于分区方法:K-Means 聚类。
26.3 K-Means 聚类
最流行的聚类方法是 K-Means。算法本身包括以下内容:
-
选择一个任意的 K K K,并随机放置 K K K个不同颜色的“中心”。
-
重复直到收敛:
-
根据最接近的中心对点进行着色。
-
将每种颜色的中心移动到具有该颜色的点的中心。
-
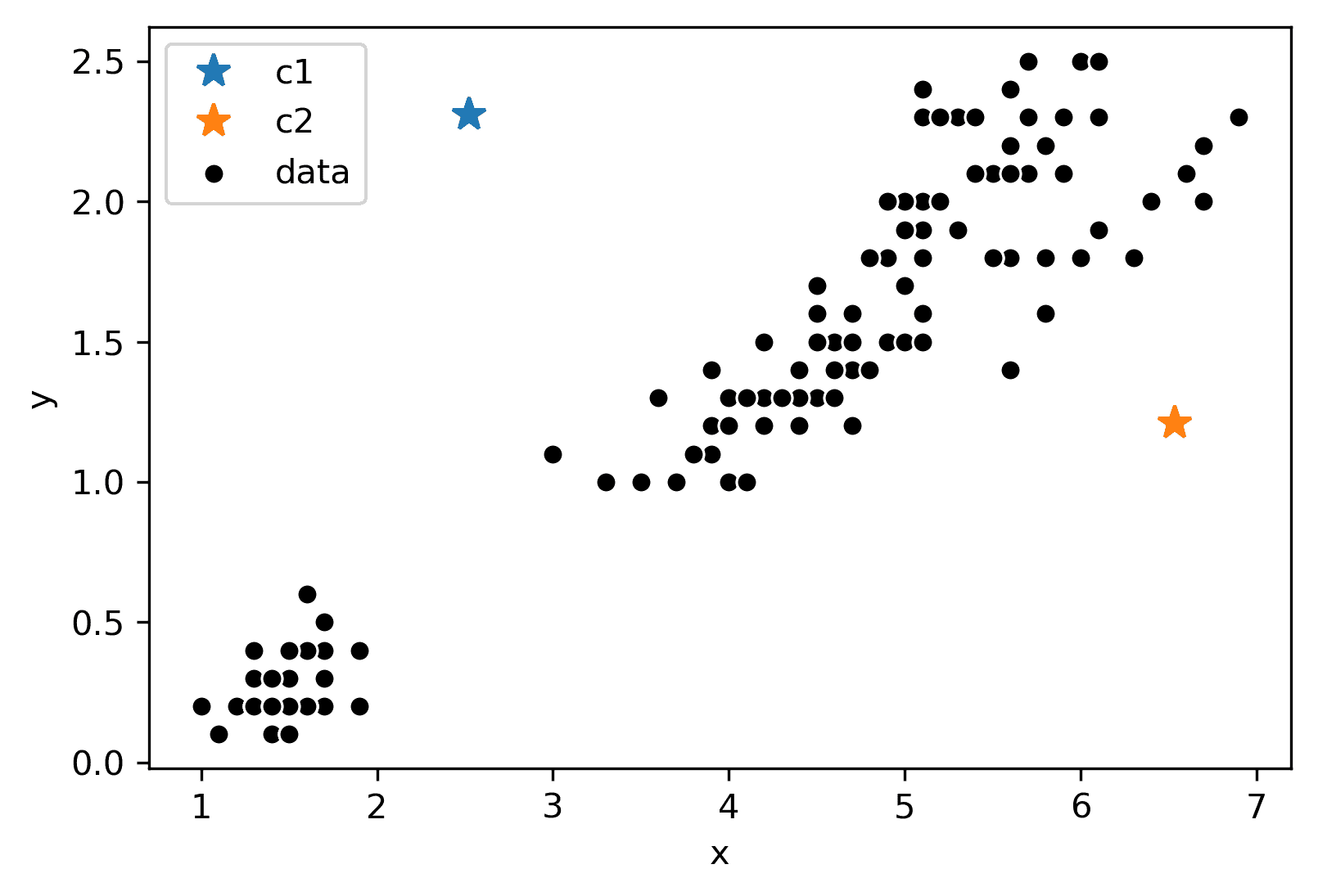
考虑以下具有任意 K = 2 K = 2 K=2和随机放置的不同颜色(蓝色、橙色)“中心”的数据:
现在,我们将遵循算法的其余部分。首先,让我们根据最接近的中心对每个点进行着色:
接下来,我们将把每种颜色的中心移动到具有该颜色的点的中心。请注意,中心通常在其颜色共享的数据中心位置。
假设这个过程(重新着色,重新设置中心)重复了几次迭代,我们最终达到了这个状态。
在这次迭代之后,中心保持不动,根本不移动。因此,我们已经收敛,聚类完成了!
26.3.0.1 注意
一个快速的说明:K-Means 是一种完全不同的算法,与 K-最近邻算法完全不同。K-Means 用于聚类,其中每个点被分配到 K K K个簇中的一个。另一方面,K-最近邻算法用于分类(或更少见的回归),预测值通常是训练集中 K K K个最近数据点中最常见的类。这些名称可能相似,但实际上没有任何共同之处。
26.4 最小化惯性
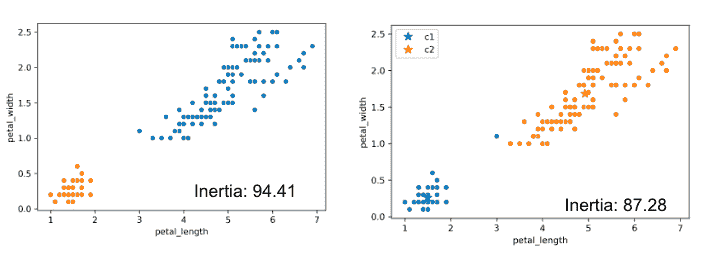
考虑以下 K = 4 K = 4 K=4的例子:
由于 K K K中心初始化/开始的随机性,每次运行 K-Means 都会得到不同的输出/聚类。考虑三种可能的 K-Means 输出;算法已经收敛,颜色表示它们被聚类为的最终簇。
哪种聚类输出是最好的?要评估不同的聚类结果,我们需要一个损失函数。
两种常见的损失函数是:
-
惯性:每个数据点到其中心的平方距离的总和。
-
畸变:每个数据点到其中心的平方距离的加权和。
在上面的例子中:
-
计算的惯性: 0.4 7 2 + 0.1 9 2 + 0.3 4 2 + 0.2 5 2 + 0.5 8 2 + 0.3 6 2 + 0.4 4 2 0.47^2 + 0.19^2 + 0.34^2 + 0.25^2 + 0.58^2 + 0.36^2 + 0.44^2 0.472+0.192+0.342+0.252+0.582+0.362+0.442
-
计算失真: 0.4 7 2 + 0.1 9 2 + 0.3 4 2 3 + 0.2 5 2 + 0.5 8 2 + 0.3 6 2 + 0.4 4 2 4 \frac{0.47^2 + 0.19^2 + 0.34^2}{3} + \frac{0.25^2 + 0.58^2 + 0.36^2 + 0.44^2}{4} 30.472+0.192+0.342+40.252+0.582+0.362+0.442
回到本节开头的四簇示例,random.seed(25)的惯性为44.96,random.seed(29)的惯性为45.95,random.seed(40)的惯性为54.35。看来最佳的聚类输出是random.seed(25),惯性为44.96!
事实证明,K-Means 试图最小化的函数是惯性,但通常无法找到全局最优解。为什么会这样?我们可以将 K-means 看作是一对轮流进行优化的优化器。第一个优化器保持中心位置恒定,并优化数据颜色。第二个优化器保持数据颜色恒定,并优化中心位置。两个优化器都没有完全控制!
这是一个困难的问题:给出一个优化给定 K K K的惯性的算法; K K K是预先选择的。你的算法应该返回确切的最佳中心和颜色,但你不需要担心运行时间。
注意:这是一个有点 CS61B/CS70/CS170 问题,所以不要太担心完全理解我们所处的棘手困境!
一个潜在的算法:
-
对于所有可能的 k^n 种着色:
-
计算该着色的 k 个中心。
-
计算 k k k个中心的惯性。
- 如果当前的惯性比已知的最佳值更好,那么写下当前的中心和着色,并将其称为新的已知最佳值。
-
尚未找到更好的算法来解决最小化惯性的问题。
26.5 分层聚类
现在,让我们考虑分层聚类。
考虑两个 K-Means 聚类输出的结果:
你更喜欢哪个聚类结果?看起来 K-Means 更喜欢右边的结果,因为它的惯性更低(每个数据点到其中心的平方距离之和),但这引发了一些问题:
-
为什么右边的惯性更低?K-Means 优化距离,而不是“blobbiness”。
-
右边的聚类“错误”吗?好问题!
现在,让我们介绍分层聚类!我们从每个数据点在一个单独的簇开始,然后我们将继续合并最相似的数据点/簇,直到最后只剩下一个大簇。这被称为自下而上或聚合方法。
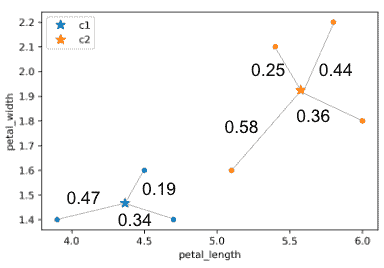
有各种方法来决定合并簇的顺序,称为链接标准:
-
单链接(最相似的相似性):两个簇之间的距离是第一个簇中的一个点与第二个簇中的一个点之间的最小距离。
-
完全链接(最不相似的相似性):两个簇之间的距离是第一个簇中的一个点与第二个簇中的一个点之间的最大距离。
-
平均链接:簇中两个点的平均相似性。
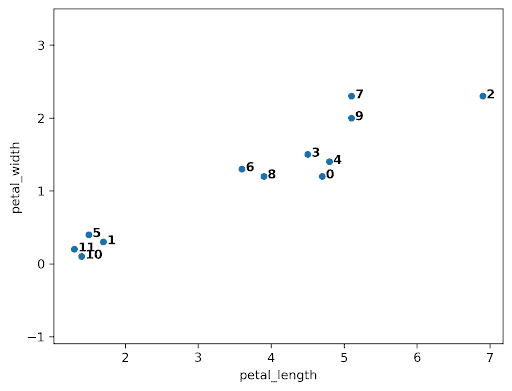
当算法开始时,每个数据点都在自己的簇中。在下面的图中,有 12 个数据点,所以算法从 12 个簇开始。随着聚类的开始,它开始评估哪些簇彼此最接近。
最接近的簇是 10 和 11,所以它们被合并在一起。
接下来,点 0 和 4 被合并在一起,因为它们最接近。
在这一点上,我们有 10 个簇:8 个单点(簇 1、2、3、4、5、6、7、8 和 9)和 2 个双点(簇 0 和 10)。
尽管簇 0 和 3 不是最接近的,但让我们考虑如果我们试图合并它们。一个棘手的问题出现了:簇 0 和 3 之间的距离是多少?我们可以使用“完全链接”方法,它使用组之间所有点对中的最大距离。
让我们假设算法运行时间稍长,并且我们已经达到了以下状态。接下来是簇 0 和 7,但为什么?0 和 6 之间的最大线长于 0 和 7 之间的最大线长。
因此,0 和 7 被合并为 0。
经过更多迭代,我们最终收敛到左侧的图。有两个簇(0,1),凝聚算法已经收敛。
请注意,在完整数据集上,我们的凝聚聚类算法实现了更“正确”的输出。
26.5.1 聚类、树状图和直觉
聚合聚类是“分层聚类”的一种形式。它是可以解释的,因为我们可以跟踪两个簇何时被合并(每个簇都是一棵树),并且我们可以可视化合并层次,从而得到“树状图”。我们不会在本课程中进一步讨论这一点,但你可能会在实际应用中看到这些。以下是一些例子:
一些教授使用凝聚聚类来进行分级分箱;如果两个人之间有很大的差距,就在那里画一个分级阈值。其想法是,等级聚类应该更像下图左侧的情况,而不是右侧的情况。
26.6 选择 K
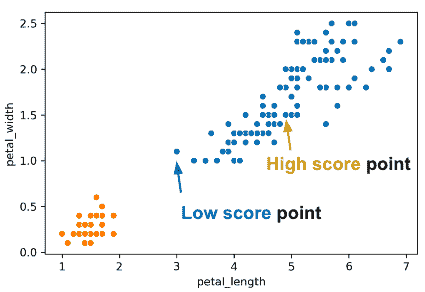
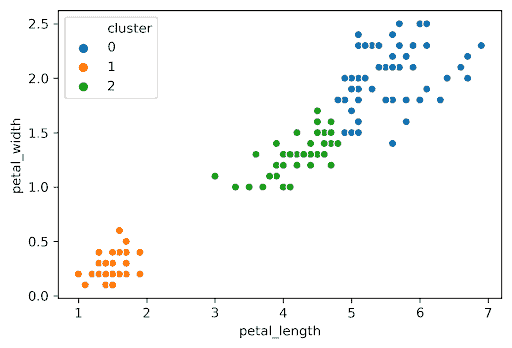
我们讨论的算法要求我们在开始之前选择 K。但是我们如何选择 K?通常,最佳的 K 是主观的。例如,考虑下面的状态图。
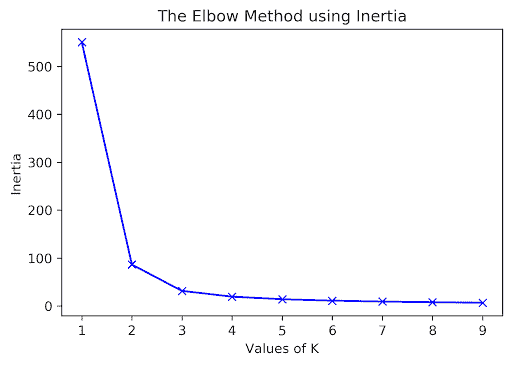
这里有多少个簇?对于 K-Means,确定这一点的一种方法是绘制惯性与许多不同的 K 值。我们会在“拐点”处选择 K,在此之后我们会得到递减的回报(请注意,大型复杂数据通常缺乏拐点,因此这种方法并不是百分之百可靠的)。在这里,我们可能会选择 K = 2。
26.6.1 轮廓分数
为了评估特定数据点的“聚类效果”如何,我们可以使用“轮廓分数”,又称“轮廓宽度”。较高的轮廓分数表示该点接近其簇中的其他点;较低的分数意味着它远离其簇中的其他点。
对于数据点 X,得分 S 是: S = B − A m a x ( A , B ) S =\frac{B - A}{max(A, B)} S=max(A,B)B−A其中 A 是到簇中其他点的距离,B 是到最近簇中点的平均距离。
考虑一下 S 的最大可能值以及该值如何出现。S 的最大可能值是 1,如果 X 的簇中的每个点都恰好在 X 的正上方;到 X 的簇中其他点的平均距离是 0,因此 A = 0。因此,S = \frac{B}{max(0, B)} = \frac{B}{B} = 1。另一种情况是 S = 1,如果 B 远大于 A(我们将其表示为 B >> A)。
S 可以是负数吗?答案是可以。如果到 X 的簇内成员的平均距离大于到最近簇的距离,那么这是可能的。例如,上图右侧的“低分”点具有 S = -0.13
26.6.2 轮廓图
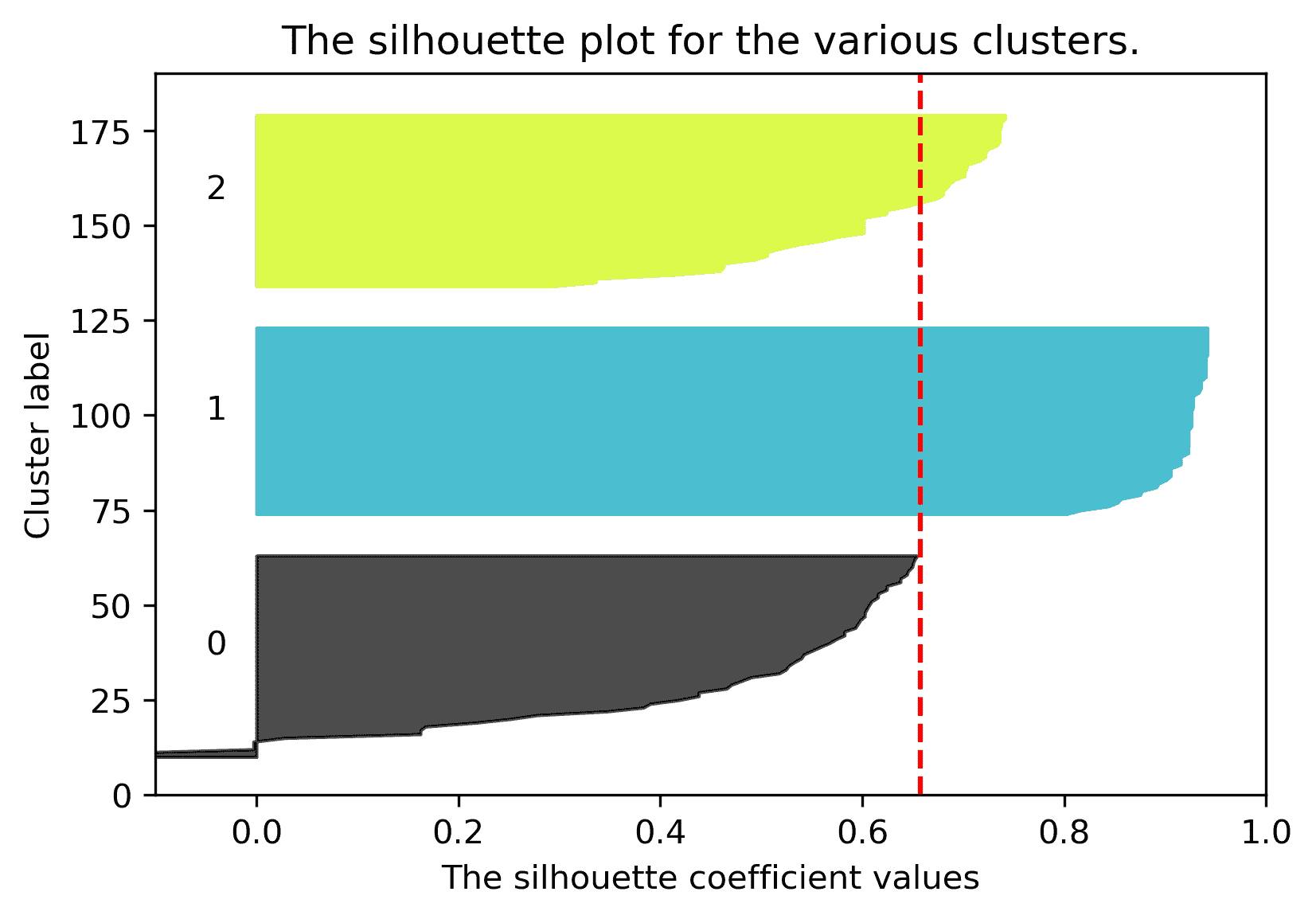
我们可以绘制所有数据点的轮廓分数。轮廓宽度较大的点深深嵌入其簇中;红色虚线显示了平均值。下面,我们绘制了 K=2 的轮廓分数。
同样,我们可以为相同的数据集绘制 K = 3 K=3 K=3 的轮廓分数:
3 个集群的平均轮廓分数较低,因此 K = 2 K=2 K=2 是更好的选择。这也符合我们的直觉。
26.6.3 选择 K:真实世界的指标
有时候你可以依靠真实世界的指标来指导你选择 K K K。对于 T 恤,我们可以
-
客户的集群高度和体重, K = 3 K = 3 K=3 设计小号、中号和大号衬衫。
-
客户的集群高度和体重, K = 5 K = 5 K=5 设计 XS、S、M、L 和 XL 衬衫。
要选择 K K K,考虑两种不同 K K K 的预期成本和销售,并选择最大化利润的那个。
26.7 结论
我们现在讨论了一个新的机器学习目标 - 聚类 - 并探讨了两种解决方案:
-
K-Means 尝试优化一个称为惯性的损失函数(没有已知的算法以有效的方式找到最佳答案)
-
层次凝聚
我们版本的这些算法需要一个超参数 K K K。有 4 种方法可以选择 K K K:直觉上、肘部法则、轮廓分数和利用真实世界的指标。
有许多机器学习问题。每个问题都可以通过许多不同的解决方案技术来解决。每个问题都有许多用于评估成功/损失的指标。许多技术可以用来解决不同的问题类型。例如,线性模型可以用于回归和分类。
我们只是触及了表面,并没有讨论许多重要的想法,比如神经网络/深度学习。我们将在最后一堂课上提供一些关于如何进一步探索这些主题的具体课程建议。