《动手学深度学习》组队学习——Task1-2打卡
一、 环境安装配置
在本次学习前已在电脑安装过Anaconda,由于条件所限暂不考虑使用GPU的情况,根据李沐老师书上的安装步骤进行尝试,并作如下记录。
1.在Navigator界面,尝试创建d2l环境,并在base和d2l环境下安装了pytorch(咱也不知道这步是不是多余)。
2.根据书上的安装步骤进行torch和d2l包的安装,期间出现一些因网络连接错误造成的失败情况,重新安装后得到解决。
3.使用书中的代码进行D2L notebook的下载,成功!然后激活d2l环境,安装d2l和torch包(花费了太多时间)。
conda activate d2l
pip install d2l torch torchvision
4.最后进入Jugyter notebook是这样的。
存一个退出d2l环境的代码
conda deactivate
二、预备知识
1. 数据操作
(1)若张量 X ∈ R n 1 × ⋯ × n d \mathcal{X}\in\mathbb{R}^{n_1\times\cdots\times n_d} X∈Rn1×⋯×nd在代码中用x表示,那么,x.shape将会输出 ( n 1 , … , n d ) (n_1,\dots,n_d) (n1,…,nd),x.numel()将输出 N : = ∏ i = 1 d n i N:=\prod^{d}_{i=1}n_i N:=∏i=1dni,len(x)将输出 n 1 n_1 n1.
(2)torch张量与Numpy数组的转化
A = X.numpy()
B = torch.tensor(A)
2.数据预处理
(1)数值型变量,序列均值填补缺失值
x = x.fillna(x.mean())
(2)离散型或分类变量,将“Nan”视为一个类别,进行0-1变量转化
x = pd.get_dummies(x, dummy_na=True)
3.线性代数
(1)非降维求和
A.sum(axis=1, keepdims=True)
(2)张量的Frobenius范数
∥ X ∥ F = ∑ i 1 = 1 n 1 ⋯ ∑ i d = 1 n d x i 1 ⋯ i d 2 \|\mathcal{X}\|_F=\sqrt{\sum_{i_1=1}^{n_1}\cdots\sum_{i_d=1}^{n_d}x_{i_1\cdots i_d}^2} ∥X∥F=i1=1∑n1⋯id=1∑ndxi1⋯id2
torch.norm(torch.ones((2, 4, 8)))
(3)形状为(2, 3, 4)的张量,在轴0、1、2上的求和输出
T = torch.ones(2,3,4)
T.sum(axis=0), T.sum(axis=1), T.sum(axis=2)
4.微积分
(1)绘制函数 g ( y ) = y 3 − 1 y g(y)=y^3-\frac{1}{y} g(y)=y3−y1和其在 y = 1 y=1 y=1处切线的图像。
def g(y):
return y**3-1/y
y = np.arange(0, 3, 0.1)
plot(y, [g(y), 4*y-4], 'y', 'g(y)', legend=['g(y)', 'Tangent line (y=1)'])
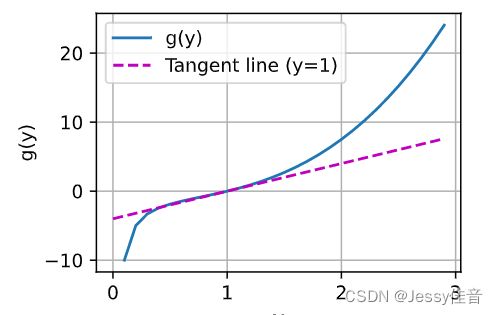
(2)函数 f ( x ) = 3 x 1 2 + 5 e x 2 f(\mathbf{x})=3x_1^2+5e^{x_2} f(x)=3x12+5ex2, g ( x ) = ∥ x ∥ 2 g(\mathbf{x})=\|\mathbf{x}\|_2 g(x)=∥x∥2的梯度
g r a d f ( x ) = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 ] = [ 6 x 1 , 5 e x 2 ] g r a d g ( x ) = 2 x gradf(\mathbf{x})=\left[\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}\right]=\left[6x_1, 5e^{x_2}\right]\\ gradg(\mathbf{x})=2\mathbf{x} gradf(x)=[∂x1∂f,∂x2∂f]=[6x1,5ex2]gradg(x)=2x
(3)函数 u = f ( x , y , z ) u=f(x,y,z) u=f(x,y,z)的链式法则,其中 x = ( a , b ) , y = ( a , b ) , z = ( a , b ) x=(a,b), y=(a,b), z=(a,b) x=(a,b),y=(a,b),z=(a,b).
d u d a = ∂ f ∂ x d x d a + ∂ f ∂ y d y d a + ∂ f ∂ z d z d a d u d b = ∂ f ∂ x d x d b + ∂ f ∂ y d y d b + ∂ f ∂ z d z d b \frac{du}{da}=\frac{\partial f}{\partial x}\frac{d x}{da}+\frac{\partial f}{\partial y}\frac{d y}{da}+\frac{\partial f}{\partial z}\frac{d z}{da}\\ \frac{du}{db}=\frac{\partial f}{\partial x}\frac{d x}{db}+\frac{\partial f}{\partial y}\frac{d y}{db}+\frac{\partial f}{\partial z}\frac{d z}{db} dadu=∂x∂fdadx+∂y∂fdady+∂z∂fdadzdbdu=∂x∂fdbdx+∂y∂fdbdy+∂z∂fdbdz
5.自动微分
(1)反向传播计算y对x每个分量的梯度
y.backward() #标量
y.sum().backward() #非标量
x.grad
参考文献
https://zh-v2.d2l.ai/index.html

