【上分日记】第369场周赛（分类讨论 + 数学 + 前缀和）

前言

 终于考完试了，考了四天，也耽搁了四天，这就赶紧来补这场周赛的题了，这场周赛博主只写了两道题，第一题和第三题 ( hhh, 菜鸡勿喷)，这场周赛挺有难度，也挺有意思的，第二题是个国际象棋，我都没下过，分类讨论也是有点困难。做出来的也有思路不顺的，下面我们把这四道题从头到尾总结一下。

正文

1.3000. 对角线最长的矩形的面积

• 题目链接：对角线最长的矩形的面积

• 题目思路：

1. 先求出对角线的平方，等同于计算对角线。
2. 不断更新最长的对角线的平方与其面积，如果相等，则取面积最大的。

• 实现代码：

class Solution {
public:
    int areaOfMaxDiagonal(vector<vector<int>>& dimensions) 
    {
        int diag = 0;
        int area = 0;
        for(auto v : dimensions)
        {
            int val = v[0]*v[0] + v[1]*v[1];
            int s = v[0]*v[1];
            if(val > diag ||(val == diag && s > area))
            {
                diag = val;
                area = s;
            }
        }
        return area;    
    }
};

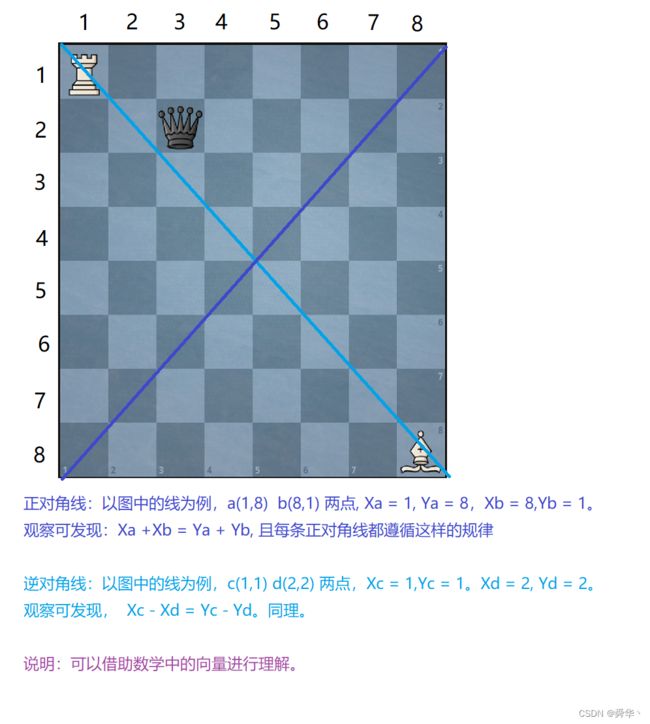
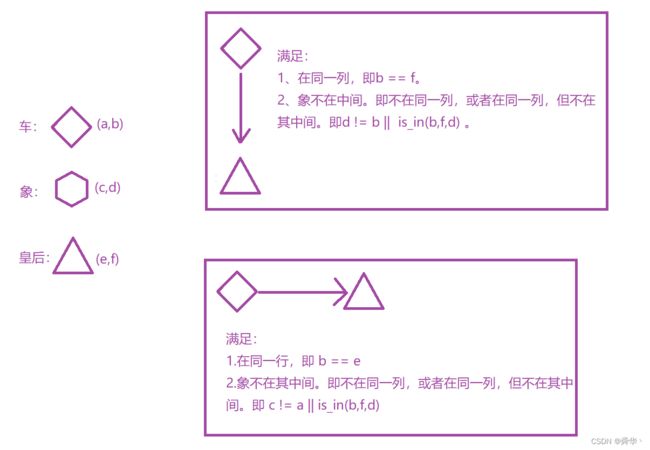
2.3001. 捕获黑皇后需要的最少移动次数

• 题目链接：捕获黑皇后需要的最少移动次数

• 数学知识:
  

• 说明：这个不知道，写这道题难度会上升不少。

• 我们先来进行分类讨论。

1. 车
   1.1 车一步到达：
   

• 说明： 闪击战术
  
  2.2 车两步到达，只要不是一步，必然是两步到达。

2. 象
   2.1 象一步到达。
   
   2.2 象两步，或者如果象与皇后所在格子的颜色不同的话，只移动象是到不了皇后的。

• 总结，因为有车兜底，所以最多两步，一步的话分情况讨论即可。

• 实现代码：

class Solution {
public:
    int minMovesToCaptureTheQueen(int a, int b, int c, int d, int e, int f) 
    {
        //先分析车的
        auto is_in = [&](int left,int right,int x)
        {
            int _left  = min(left,right);
            int _right = max(left,right);
            return !(x >_left && x <_right);
        };
        auto check_car = [&]()
        {
            if(
               ( e == a && (c != a || is_in(f,b,d)) )//行相等
            || ( f == b && (d != b || is_in(e,a,c)) ) //列相等
            ) 
             return 1;
            

            return 2;
        };
        auto check_ele = [&]()
        {
            if(
                (c + f == e + d &&(c + b != a + d || is_in(c,e,a)) //正对角线
                || (c - f == e - d && (c -b != a - d || is_in(c,e,a))))//逆对角线
            )
                return 1;
            
            return 2;
        };

        return min(check_car(),check_ele());
    }
};

3.3002. 移除后集合的最多元素数

• 题目链接：移除后集合的最多元素数

• 题目思路：

• 在实际过程中，博主是模拟进行求解的，即先将集合分别去重，然后去掉集合元素较多的两个集合的共同元素，然后取两个长度与原本的长度的二分之一进行比较，取较小的。最后返回两者之和即可。

class Solution {
public:
    int maximumSetSize(vector<int>& nums1, vector<int>& nums2) 
    {
        //第一步：对自身去重
        unordered_set<int> gather1(nums1.begin(),nums1.end()),\
        gather2(nums2.begin(),nums2.end());
        
        int ans1 = gather1.size(),ans2 = gather2.size()\
        ,sz1 = nums1.size() / 2,sz2 = nums2.size() / 2;
        
        //第二步：去掉两个集合中重复的，且去的是较长的那一个。
        for(auto e : gather1)
        {
            if(gather2.count(e))
            {
                if(ans2 > ans1)
                    ans2--;
                else
                    ans1--;
            }
        }
        //第三步：取min求预期值。
        return min(ans1,sz1) + min(ans2,sz2);
    }
};

• 看了灵神的题解，直接进行讨论也可以，是利用重复元素出现的个数，要想达到最长，关键是先去重复的，然后再去不重复的。

• 实现代码：

class Solution {
public:
    int maximumSetSize(vector<int>& nums1, vector<int>& nums2) 
    {
        unordered_set<int> gather1(nums1.begin(),nums1.end())\
        ,gather2(nums2.begin(),nums2.end());
        //第一步对自身去重

        //第二步求出并集的个数
        int key = 0;
        for(auto e : gather1)
        {
            if(gather2.count(e)) key++;
        }
        //第三步分类讨论
        //优先取消并集元素,也就是并集元素有两条命。
        int ans1 = gather1.size(),sz1 = nums1.size() / 2;
        int ans2 = gather2.size(),sz2 = nums2.size() / 2;
        auto ajust = [&](int ans,int sz)
        {
            if(ans > sz)
            {
                int need = ans - sz;
                if(key > need)
                {
                    key -= need; ans -= need,need = 0;
                }
                else
                {
                    need -= key; ans -= key; key = 0;
                }
                ans -= need;
            }
            return ans;
        };
        return ajust(ans1,sz1) + ajust(ans2,sz2) - key;
    }
};

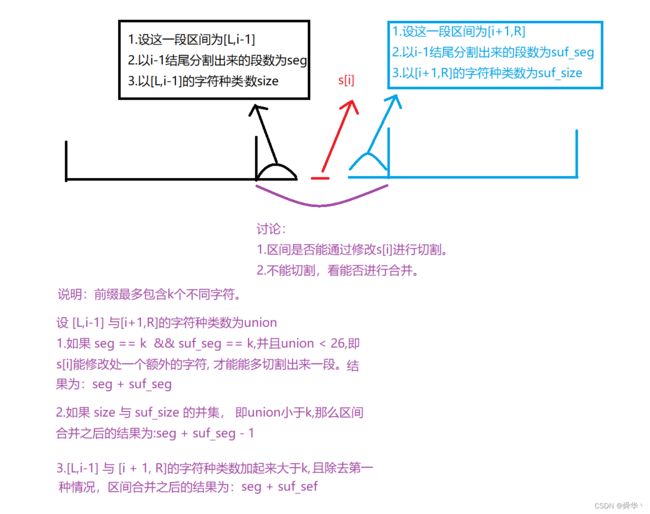
3.3003. 执行操作后的最大分割数量

• 题目链接：执行操作后的最大分割数量
• 题目大致意思：

1. 我们只能执行一次，即 将s[i] 修改为 26个字母中的一个。
2. 且 i 只能在前缀s 中。
3. 求最大分割数量。

• 前置知识：

• s从前往后分割，与s从后往前分割，段数相同。

• 题目思路：

class Solution {
public:
    int maxPartitionsAfterOperations(string s, int k) 
    {
       /*
         如果总的字符串小于k，即使修改一个字符，也只能等于k，
         还是只能划分一段。
       */
        int mask = 0,kinds = 0;
        for(char ch : s)
        {
            int key = 1 << (ch - 'a');
            if(!(mask & key))
            {
                ++kinds;
                mask |= key;
            }
        }
        if(kinds < k || k == 26) return 1;
         /*
          如果需要的字符串种类等于26，那么只能切到最后，
          且无法再通过修改字符，增加段数。
        */
        int sz = s.size(),seg = 1;
        kinds = 0,mask = 0;
        vector<pair<int,int>> suf(sz + 1);
        /*
          mask:   用于位运算记录字符种类的掩码。
          segment:段，记录前缀或者后缀的分成的段数，
                  最少划分一段。
          suffix: 后缀，即suf,记录能划分的段数与最
                  近一段的mask。
        */
        auto update = [&](int i)
        {
                
            int key =  1 << (s[i] - 'a');
            if(!(mask & key))
            {
                //记录字符串的种类。
                mask |= key;
                if(++kinds > k)
                {

                    /*
                      此时key也在mask里面。
                    */
                    seg++;
                    mask = key;
                    kinds = 1;

                }
            }
            return;
        };
        for(int i = sz - 1; i >= 0; i--)
        {
            update(i);
            suf[i] = {seg,mask};
        }

        int ans = seg; //最小的分割段数，且后缀与前缀分的结果是相同的。

        seg = 1,mask = 0,kinds = 0;
        for(int i = 0; i < sz; i++)
        {
            /*
                以i为分界线进行讨论，[L,i),(i + 1, R]
            */
            auto [suf_seg,suf_mask] = suf[i+1];
            //[L,R]是多于的一段，这一段，也可能可以划分。
            int res = suf_seg + seg;
            //默认为其它情况，其它情况是在此基础上进行加一或者减一。
            int unionmask = suf_mask | mask;
            if(__builtin_popcount(unionmask) < k)
            {
                //只能合并，且会少一段
                res--;
            }
            else if(__builtin_popcount(suf_mask) == k && kinds == k
                &&__builtin_popcount(unionmask) < 26)
            {
                //会多出一个s[i]字符，因此会增加一段
                res++;
            }
            //更新三种情况的最大值。
            ans = max(ans,res); 
            update(i);
        }
        return ans;
    }
};

• 注 :本题的思路主要参考灵神的题解。

总结

 综合来说，这几道题都侧重于分类讨论，其中还牵扯到一些数学的知识，以及有趣的国际象棋，最后一题则需要借助前后缀 + 数学知识 + 分类讨论进行判断。

尾序

 我是舜华，期待与你的下一次相遇！