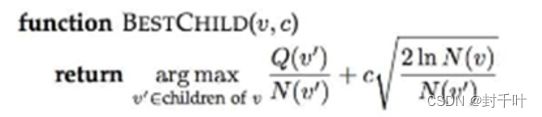蒙特卡洛树搜索python实现
1.前言
本文仅适合作为理解蒙特卡洛树搜索的最后一篇文章,原理我懒得写,完全没看过的自己先看其他博文,只写代码实现。
2.伪代码图
相信大家都看过这张图很多次了,但就是看不懂,本文将严格按照这张流程图,进行实现。
先解释一下几个难理解的点:
s表示状态,v表示节点
s(v): 与节点v相关的状态
a(v): 产生v节点的动作
A(s): 状态s的可执行动作
N(v): 访问过v的次数
Q(v): 总共的对于v的仿真reward
s=f(s,a): 该函数表示状态s执行动作a获得新状态s
3.具体实现
3.1 UCTsearch
def UCTsearch(s0, times): #times参数是为了控制计算次数
v0 = Node(s0, None) # 基于初态s0,创建根节点v0
for i in range(times): # 在计算开销预算内
vl = TreePolicy(v0) # 选择
delta = DefaultPolicy(copy.deepcopy(vl.state)) # 模拟
BackUp(vl, delta) # 反向传播
return BestChild(v0, 0).state.parent_action #返回产生该节点的动作3.2 TreePolicy
def TreePolicy(v): #选择
while not v.is_terminal_node(): # 为非终结节点时
if not v.is_all_expand(): # 没有完全扩展
return Expand(v)
else:
v = BestChild(v, 1)
return v3.3 Expand
def Expand(v): #扩展
new_state = v.state.random_do_untried_action() # 随机执行未执行的可执行动作
v1 = Node(new_state, v) # 为该状态建立节点,并成为v的子节点
v.add_child(v1)
return v13.4 BestChild
def BestChild(v, c): #返回v的最优子节点,c用于控制是否加上探索价值
return max(v.children, key=lambda v1: (v1.Q / v1.N) + c * math.sqrt(2.0 * math.log(v.N) / v1.N))3.5 DefaultPolicy
def DefaultPolicy(s): #模拟
while not s.is_terminal_state(): # 为非终结状态时
s = s.random_do_untried_action() # 随机执行可执行动作获得新状态
return s.reward() # 返回该状态奖励3.6 BackUp
def BackUp(v, delta): # 反向传播
while v is not None: # 节点非空
v.N = v.N + 1
v.Q = v.Q + delta
v = v.parent3.7 Node
定义树节点
class Node(object):
def __init__(self, state, parent):
self.parent = parent #父节点
self.children = []
self.N = 0 # 浏览次数
self.Q = 0 # 奖励
self.state = state # 承载的具体局面
def is_all_expand(self): # 是否完全扩展
return len(self.state.untried_action) == 0
def is_terminal_node(self): # 是否是终结节点
return self.state.is_terminal_state()
def add_child(self, child_node):
self.children.append(child_node)3.8 State
根据游戏类型定义具体局面,以下代码为state类的实现模板,需根据不同类型游戏增添或补全。大家在做自己的游戏时,仅需修改state类即可。
class State(object):
def __init__(self, situation):
self.situation = situation # 表示游戏具体状态,可以为列表或其他形式表示
self.all_action = [] # 所有可执行动作
self.untried_action = [] # 所有未执行过的可执行动作
self.parent_action = None # 产生该状态的动作
def reward(self): # 对于根玩家而言,赢返回1,输返回-1
def do_action(self, action): # 执行动作action,并返回新状态new_s
next_situation = copy.deepcopy(self.situation) # 深复制
# 补充语句: 执行动作获得next_situation
next_state = State(next_situation)
next_state.parent_action = action
return next_state
def random_do_untried_action(self): # 随机未执行的可执行动作,并返回新状态new_s
action = random.choice(self.untried_action)
next_state = self.do_action(action)
self.untried_action.remove(action)
return next_state
def is_terminal_state(self): # 判断是否为终结状态,是返回True,不是返回False4.四子棋游戏示例
注意,对于该示例,仅修改了state类和增加了运行主函数
4.1 四子棋state类
class State(object):
def __init__(self, situation, p_player, player, round_index):
self.round_index = round_index # 游戏回合数
self.p_player = p_player # 根状态玩家,表示为谁而搜索
self.player = player # 当前状态玩家,轮到谁下棋
self.situation = situation # 具体棋盘
self.all_action = [] # 所有可执行动作
self.untried_action = [] # 未执行的可执行动作
self.parent_action = None # 产生该状态的动作
self.make_all_action() # 产生动作
# print(self)
def reward(self): # 以根玩家视角看输赢,而不是当前状态玩家
if self.parent_action == None:
return 0
x = self.parent_action[0]
y = self.parent_action[1]
p = -self.player # 上一个动作执行者
flag = 0
for i in range(-3, 4):
if 0 <= y + i <= 4:
if self.situation[x][y + i] == p: # 左右
flag += 1
else:
flag = 0
if flag > 3:
return p * self.p_player
else:
continue
flag = 0
for i in range(-3, 4):
if 0 <= x + i <= 4:
if self.situation[x + i][y] == p: # 上下
flag += 1
else:
flag = 0
if flag > 3:
return p * self.p_player
else:
continue
flag = 0
for i in range(-3, 4):
if 0 <= x + i <= 4 and 0 <= y + i <= 4:
if self.situation[x + i][y + i] == p: # 斜下
flag += 1
else:
flag = 0
if flag > 3:
return p * self.p_player
else:
continue
flag = 0
for i in range(-3, 4):
if 0 <= x + i <= 4 and 0 <= y - i <= 4:
if self.situation[x + i][y - i] == p: # 斜上
flag += 1
else:
flag = 0
if flag > 3:
return p * self.p_player
else:
continue
return 0
def make_all_action(self):
for i in range(5):
for j in range(5):
if self.situation[i][j] == 0:
self.all_action.append([i, j])
self.untried_action.append([i, j])
def do_action(self, action):
next_situation = copy.deepcopy(self.situation)
next_situation[action[0]][action[1]] = self.player
next_state = State(next_situation, self.p_player, -self.player, self.round_index + 1)
next_state.parent_action = action
return next_state
def random_do_untried_action(self):
action = random.choice(self.untried_action)
next_state = self.do_action(action)
self.untried_action.remove(action)
return next_state
def is_terminal_state(self):
if self.reward() != 0: # 产生输赢
return True
else:
for i in range(5):
for j in range(5):
if self.situation[i][j] == 0:
return False
return True
def out(self):
for j in range(5):
for k in range(5):
if self.situation[j][k] == 0:
print('-',end=' ')
elif self.situation[j][k] == 1:
print('*',end=' ')
else:
print('o',end=' ')
print(end='\n')
def __repr__(self):
return "State.round_index: {}, round_player: {}, parent_action: {}, reward: {} ,self.untried_action: {}".format(
self.round_index, self.player, self.parent_action, self.reward(), len(self.untried_action))4.2 运行方法
if __name__ == "__main__":
situation = [[0, 0, 0, 0, 0], # 5*5棋盘
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]]
s = State(situation, 1, 1, 1) # 初始化状态
for i in range(100):
print(s)
s.out()
if s.is_terminal_state() == True:
print('over' + str(s.reward()))
sys.exit(0)
# if i % 2 == 0: # 取消注释进行人机对战
# a, b = map(int, input('请输入:').split(','))
# action = [a, b]
# s = s.do_action(action)
# s.p_player *= -1
else:
action = UCTsearch(s, 5000) # 运行太久可减小参数
s = s.do_action(action)
s.p_player *= -1 # 转换角色