Consistency Models

一致性模型

论文地址：https://arxiv.org/abs/2303.01469

项目地址：https://github.com/openai/consistency_models

Abstract

扩散模型在图像、音频和视频生成方面取得了重大突破，但它们依赖于迭代生成过程，这会导致采样速度慢，并限制其实时应用的潜力。为了克服这一限制，我们提出了一致性模型，这是一种新的生成模型家族，可以在没有对抗性训练的情况下实现高样本质量。它们支持通过设计快速一步生成，同时仍然允许进行几步采样，以换取计算和样本质量。它们还支持零样本数据编辑，如图像修复、彩色化和超分辨率，而无需对这些任务进行显性训练。一致性模型可以作为提取预先训练的扩散模型的一种方式进行训练，也可以作为独立的生成模型进行训练。通过广泛的实验，我们证明它们在一步和几步生成中优于现有的扩散模型蒸馏技术。例如，我们在CIFAR10上实现了新的最先进的FID 3.55，在ImageNet 64上实现了FID 6.20，用于一步生成。当被训练为独立的生成模型时，一致性模型在标准基准上也优于单步非对抗性生成模型，如CIFAR-10、ImageNet 64和LSUN 256。

1. 简介

扩散模型（Sohl-Dickstein et al，2015；Song&Ermon，2019；2020；Ho et al，2020；Song et al，2021），也称为基于分数的生成模型，在多个领域取得了前所未有的成功，包括图像生成（Dhariwal&Nichol，2021；Nichol et al，2021；Ramesh et al，2022；Saharia et al，1922；Rombach et al（2022），音频合成（Kong等人，2020；Chen等人，2021；Popov等人，2021）和视频生成（Ho等人，2022b；a）。与生成对抗性网络（GANs，Goodfellow等人（2014）），这些模型不依赖于对抗性训练，因此不太容易出现不稳定训练和模式崩溃等问题。此外，扩散模型并不像自回归模型那样对模型架构施加严格的约束（Bengio&Bengio，1999；Uria等人，2013；2016；Van Den Oord等人，2016），变分自编码器（VAEs，Kingma&Welling（2014）；Rezende等人（2014）），或归一化流（Dinh等人，2015；2017；Kingma和Dhariwal，2018）。

扩散模型成功的关键是其迭代采样过程，该过程从随机噪声向量中逐步去除噪声。这种迭代优化过程反复评估扩散模型，允许计算与样本质量的权衡：通过使用额外的计算进行更多的迭代，小型模型可以展开到更大的计算图中，并生成更高质量的样本。迭代生成对于扩散模型的零样本数据（zero-shot data）编辑功能也至关重要，使其能够解决从图像修复、彩色化、stroke-guided图像编辑到计算机断层扫描（CT）成像和核磁共振（MRI）成像等具有挑战性的逆问题（Song&Ermon，2019；Song et al，2021；2022；2023；Kawar et al，2021；2022，Chung et al，2023；Meng et al；2021）。然而，与GAN、VAE和归一化流等单步生成模型相比，扩散模型的迭代生成过程通常需要10–2000倍的计算（Song&Ermon，2020；Ho et al，2020；Song et al，2021；Zhang&Chen，2022；Lu et al（2022）），这导致推理缓慢并且限制了它们的实时应用。

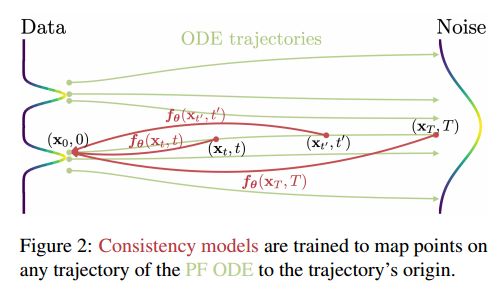
我们的目标是创建生成模型，在不牺牲迭代优化的重要优势的情况下，促进高效的单步生成。这些优势包括在必要时权衡计算和样本质量的能力，以及执行零样本数据编辑任务的能力。如图1所示，我们在连续时间扩散模型（Song等人，2021）中的概率流（PF）常微分方程（ODE）的基础上构建，其轨迹平稳地将数据分布转换为可控制的噪声分布。我们建议学习一个模型，该模型将任何时间步长的任何点映射到轨迹的起点。我们模型的一个显著特性是自洽性：同一轨迹上的点映射到同一初始点。因此，我们将此类模型称为一致性模型。一致性模型允许我们生成数据样本（ODE轨迹的初始点，例如，图1中的$x_0$），通过转换随机噪声向量（ODE轨迹的端点，例如，在图1中的$x_T$），只需一次网络评估。重要的是，通过在多个时间步长链接一致性模型的输出，我们可以提高样本质量并以更多计算为代价执行零样本数据编辑，这与迭代求精对扩散模型的支持类似。

为了训练一致性模型，我们提供了两种基于增强自洽性属性的方法。第一种方法依赖于使用数值ODE求解器和预先训练的扩散模型来生成概率流（PF） ODE轨迹上的成对相邻点。通过最小化这些对的模型输出之间的差异，我们可以有效地将扩散模型提取为一致性模型，这允许通过一个网络评估生成高质量的样本。相比之下，我们的第二种方法完全消除了对预先训练的扩散模型的需要，使我们能够孤立地训练一致性模型。这种方法将一致性模型定位为一个独立的生成模型家族。至关重要的是，这两种方法都不需要对抗性训练，而且这两种训练方法都允许灵活的神经网络架构用于一致性模型。

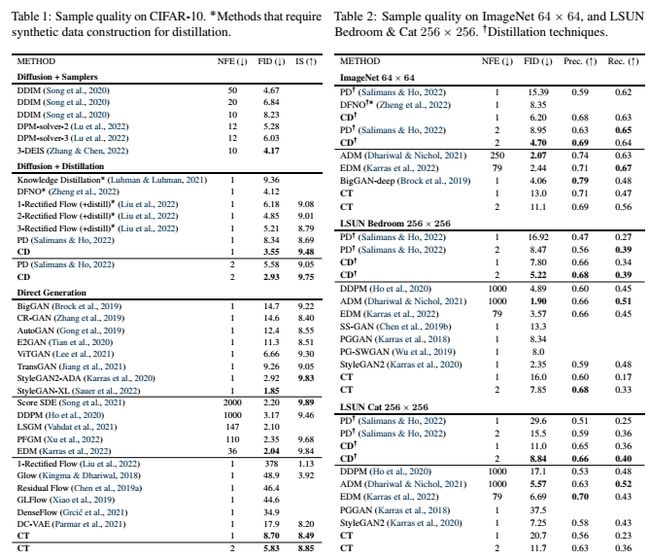
我们证明了一致性模型在几个具有挑战性的图像基准上的有效性，包括CIFAR-10（Krizhevsky等人，2009）、ImageNet 64×64（Deng等人，2009年）和LSUN 256×256（Yu等人，2015）。根据经验，我们观察到，作为一种蒸馏方法，一致性模型在各种数据集和采样步骤数量上都优于渐进蒸馏（Salimans&Ho，2022）。在CIFAR-10上，一致性模型达到了最先进的一步和两步生成的3.55和2.93的FID。在ImageNet 64上，它分别通过一次和两次网络评估实现了6.20和4.70的破纪录FID。当作为独立的生成模型进行训练时，一致性模型在单步生成中实现了与渐进蒸馏相当的性能，尽管无法访问预先训练的扩散模型。它们能够在多个数据集上胜过许多Gan和所有其他非对抗性的单步生成模型。我们还表明，一致性模型可以用于执行零样本数据编辑任务，包括图像去噪、插值、修复、彩色化、超分辨率和stroke-guided 图像编辑（SDEdit，Meng等人（2021））。

2. 扩散模型

一致性模型深受（连续时间）扩散模型理论的启发（Song等人，2021）。扩散模型通过高斯扰动将数据逐渐扰动为噪声，然后通过顺序去噪步骤从噪声中创建样本，从而生成数据。让$p_{data}(x)$表示数据分布。扩散模型从用随机微分方程（SDE）扩散$p_{data}(x)$开始（Song等人，2021；Karras等人，2022年）:
$$\mathrm{d}{\mathbf{x}}_t=\mathbf{\mu }({\mathbf{x}}_t,t)\mathrm{d}t+\sigma (t)\mathrm{d}{\mathbf{w}}_t,\text{\hspace{1em}(1)}$$
其中$t\in [0,T],T>0$是一个固定常数，$\mu (\cdot ,\cdot )$和$g(\cdot )$分别是漂移系数和扩散系数，$\{w_t{\}}_{t\in [0,T]}$；$T_s$表示标准布朗运动。我们将$x_t$的分布表示为$p_t(x)$，结果是$p_0(\mathbf{x})\equiv p_{\mathrm{data}}(\mathbf{x})$。此SDE的一个显著特性是存在一个常微分方程（ODE），Song等人（2021）将其称为概率流（PF）ODE，其在t处采样的解轨迹根据$p_t(x)$分布：
$$\mathrm{d}{\mathbf{x}}_t=\left[\mu ({\mathbf{x}}_t,t)-\frac{1}{2}\sigma (t{)}^2\nabla \log p_t({\mathbf{x}}_t)\right]\mathrm{d}t.\text{\hspace{1em}(2)}$$
这里$\nabla \log p_t({\mathbf{x}}_t)$是$p_t(x)$的得分函数；因此，扩散模型也称为基于分数的生成模型（Song&Ermon，2019；2020；Song等人，2021）。

通常，公式（1）中的SDE被设计为使得$p_T(x)$接近于可处理的高斯分布$\pi (x)$。此后，我们采用了Karras等人（2022）中的配置，他们设置了$\mu (x;t)=0$和$\sigma (t)=\sqrt{2t}$。在这种情况下，我们有$\begin{array}{c}{p}_t(\mathbf{x})=p_{\mathrm{data}}(\mathbf{x})\otimes \mathcal{N}(0,t^2\mathbf{I})\end{array}$，其中$\otimes$表示卷积运算，$\pi (x)=\mathcal{N}(0,t^2\mathbf{I})$。对于采样，我们首先通过分数匹配训练分数模型$s_{\varphi }(x,t)\approx \nabla \log p_t({\mathbf{x}}_t)$（Hyvarinen&Dayan，2005；Vincent，2011；Song等人，2019；Song&Ermon，2019；Ho等人，2020），然后将其代入公式（2）以获得概率流（PF） ODE的经验估计，其形式为
$$\frac{\mathrm{d}{\mathbf{x}}_t}{\mathrm{d}t}=-t{\mathbf{s}}_{\varphi }({\mathbf{x}}_t,t)\text{\hspace{1em}(3)}$$
我们称方程（3）为经验概率流（PF） ODE。接下来，我们对${\hat{\mathbf{x}}}_T\sim \pi =\mathcal{N}(0,T^2\mathbf{I})$进行采样，以初始化经验概率流（PF） ODE并使用任何数值ODE求解器，如Euler（Song等人，2020；2021）和Heun求解器（Karras等人，2022），在时间上向后求解，以获得解轨迹$\{{\hat{\mathbf{x}}}_T{\}}_{t\in [0,T]}$。由此产生的$x_0$可以被视为来自数据分布$p_{data}(\mathbf{x})$的近似样本。为了避免数值不稳定，通常会将求解器停止在$t=ϵ$，其中$ϵ$是一个固定的小正数，而接受${\hat{x}}_{ϵ}$作为近似样本。根据Karras等人（2022），我们将图像中的像素值重新缩放到$[-1,1]$，然后设置$T=80$和$ϵ=0.002$。

扩散模型由于采样速度慢而受到瓶颈。显然，使用ODE求解器进行采样需要对分数模型$s_{\varphi }(x,t)$进行多次评估；这在计算上是昂贵的。现有的快速采样方法包括更快的数值常微分方程求解器（Song等人，2020；Zhang&Chen，2022；Lu等人，2022年；Dockhorn等人，2022）和蒸馏技术（Luhman&Luhman，2021；Salimans&Ho，2022，Meng等人，2022.Zheng等人，2022）。然而，ODE求解器仍然需要10个以上的评估步骤才能生成有竞争力的样本。大多数蒸馏方法，如Luhman&Luhman（2021）和Zheng等人（2022）依赖于在蒸馏之前从扩散模型中收集大量样本数据集，这本身在计算上是昂贵的。据我们所知，唯一没有这种缺点的蒸馏方法是渐进蒸馏（PD，Salimans&Ho（2022）），我们在实验中广泛比较了一致性模型。

3. 一致性模型

我们提出了一致性模型，这是一种新型的生成模型，在其设计的核心支持单步生成，同时仍然允许零样本数据编辑的迭代生成以及样本质量和计算之间的权衡。稠度模型可以在蒸馏模式或分离模式中进行训练。在前一种情况下，一致性模型将预先训练的扩散模型的知识提取到一个单步采样器中，显著改善了样品质量方面的其他蒸馏方法，同时允许使用零样本图像编辑应用。在后一种情况下，一致性模型是孤立训练的，不依赖于预先训练的扩散模型。这使它们成为一类独立的新生成模型。

下面我们介绍一致性模型的定义、参数化和采样，并简要讨论它们在零样本数据编辑中的应用。

Definition（定义） 给定解轨迹$\{x_t{\}}_{t\in [0,T]}$在公式（2）的概率流（PF） ODE中，我们将一致性函数定义为$\mathbf{f}:({\mathbf{x}}_t,t)\mapsto {\mathbf{x}}_{ϵ}$。一致性函数具有自洽性的性质：对于任意对的$(x_t;t)$，其输出是一致的，其属于相同的概率流（PF） ODE轨迹，即对于所有的$t,t^{\prime }\in [ϵ,T]$，有$\mathbf{f}({\text{x}}_{\mathbf{t}},\mathbf{t})=\mathbf{f}({\text{x}}_{{\mathbf{t}}^{\prime }},{\mathbf{t}}^{\prime })$。在固定时间自变量的情况下，$f(\cdot ,t^{\prime })$始终是一个可逆函数。如图2所示，一致性模型（符号为$f_{\theta }$）的目标是通过学习增强自洽性属性，从数据中估计该一致性函数$f$（详见第4节和第5节）。

Parameterization（参数化） 对于任何一致性函数$f(\cdot ,\cdot )$我们有$\mathbf{f}({\mathbf{x}}_{ϵ},ϵ)={\mathbf{x}}_{ϵ}$，即$f(\cdot ,ϵ)$是一个恒等函数。我们将这种约束称为边界条件。一个有效的一致性模型必须遵守这个边界条件。对于基于深度神经网络的一致性模型，我们讨论了两种几乎免费实现这种边界条件的方法。假设我们有一个自由形式的深度神经网络$F_{\theta }(x,t)$，其输出具有与$x$相同的维度。第一种方法是简单地将一致性模型参数化为：
$${\mathbf{f}}_{\mathbf{\theta }}(\mathbf{x},t)=\{\begin{array}{ll}\mathbf{x}& t=ϵ\\ F_{\mathbf{\theta }}(\mathbf{x},t)& t\in (ϵ,T]\end{array}\text{\hspace{1em}(4)}$$
第二种方法是使用跳跃连接来参数化一致性模型：
$${\mathbf{f}}_{\mathbf{\theta }}(\mathbf{x},t)=c_{\mathrm{skip}}(t)\mathbf{x}+c_{\mathrm{out}}(t)F_{\mathbf{\theta }}(\mathbf{x},t)\text{\hspace{1em}(5)}$$
其中$c_{\mathrm{skip}}(t)$和$c_{\mathrm{out}}(t)$是可微函数，使得$c_{\mathrm{skip}}(ϵ)=1$和$c_{\mathrm{out}}(ϵ)=0$。这边如果$F_{\theta }(x,t)$和标度系数可微，则一致性模型在$t=ϵ$处是可微的，这对于训练连续时间一致性模型至关重要（附录B.1和B.2）。公式（5）中的参数化与许多成功的扩散模型非常相似（Karras等人，2022；Balaji等人，2022），使得更容易借用强大的扩散模型架构来构建一致性模型。因此，我们在所有实验中都遵循第二个参数化。

Sampling（采样） 具有训练有素的一致性模型$f(\cdot ,\cdot )$，我们可以通过从初始分布${\hat{\mathbf{x}}}_T\sim \mathcal{N}(0,T^{2}I)$中采样来生成样本；，然后评估${\hat{\text{x}}}_{ϵ}={\mathbf{f}}_{\theta }({\hat{\text{x}}}_T,T)$的一致性模型。这只涉及通过一致性模型的一次前向传播，因此在单个步骤中生成样本。重要的是，还可以通过交替的去噪和噪声注入步骤来多次评估一致性模型，以提高样本质量。在算法1中总结，这种多步骤采样过程提供了以计算换取样本质量的灵活性。它在零样本数据编辑中也有重要的应用。在实践中，我们使用贪心算法在算法1中找到时间点，其中使用三元搜索来优化从算法1获得的样本的FID，一次一个地精确定位时间点。

Zero-Shot Data Editing（零样本数据编辑） 一致性模型使各种数据编辑和操作应用能够在零样本中进行；他们不需要明确的训练来执行这些任务。例如，一致性模型定义了从高斯噪声向量到数据样本的一对一映射。与GAN、VAE和归一化流等潜在变量模型类似，一致性模型可以通过遍历潜在空间来轻松地在样本之间进行插值（图11）。由于一致性模型被训练为从任何噪声输入$x_t$中恢复$x$，其中$t\in [ϵ,T]$，它们可以对各种噪声水平执行去噪（图12）。此外，算法1中的多步生成过程有助于通过使用类似于扩散模型的迭代替换过程来解决零样本中的某些逆问题（Song&Ermon，2019；Song et al，2021；Ho et al，2022b）。这使许多应用能够在图像编辑环境中进行，包括修补（图10）、彩色化（图8）、超分辨率（图6b）和stroke-guided 图像编辑（图13），如SDEdit（Meng等人，2021）。在第6.3节中，我们实证证明了一致性模型在许多零样本图像编辑任务中的能力。

4. 通过蒸馏训练一致性模型

(这部分写不下去）

5. 训练一致性模型

可以在不依赖于任何预先训练的扩散模型的情况下训练一致性模型。这与蒸馏扩散技术不同，使一致性模型成为一个新的独立生成模型家族。

在一致性蒸馏中，我们使用预先训练的分数模型$s_{\varphi }(x,t)$来近似基本事实得分函数$\nabla \log p_t({\mathbf{x}}_t)$。为了摆脱这种依赖，我们需要寻找其他方法来估计分数函数。事实上，由于以下恒等式（附录A中的引理1），存在$\nabla \log p_t({\mathbf{x}}_t)$的无偏估计量：
∇ log ⁡ p t ( x t ) = − E [ x t − x t 2 | x t ] \nabla\log p_t(\mathbf{x}_t)=-\mathbb{E}\left[\dfrac{\mathbf{x}_t-\mathbf{x}}{t^2}\middle|\mathbf{x}_t\right] ∇logpt​(xt​)=−E[t2xt​−x​ ​xt​]
其中$\mathbf{x}\sim p_{\text{data}}$和${\mathbf{x}}_t\sim \mathcal{N}(\mathbf{x};t^{2}I)$。也就是说，给定$x$和$x_t$，我们可以用$\nabla \log p_t({\mathbf{x}}_t)$和$-({\text{x}}_t-\text{x})/t^2$形成的蒙特卡罗估计。我们现在表明，这个估计实际上在一致性蒸馏中足以取代预训练的扩散模型，当使用欧拉方法（或任何更高阶方法）作为$N\to \infty$极限下的ODE求解器时。

更确切地说，我们有以下定理。

证据该证明基于泰勒级数展开和分数函数的内容（引理1）。附录A.3中提供了完整的证明。

6. 实验

我们使用一致性蒸馏和一致性训练来学习真实图像数据集上的一致性模型，包括CIFAR-10（Krizhevsky et al，2009）、ImageNet 64 v2。根据Frechet Inception Distance（FID，´Heusel et al（2017），越低越好）、Inception Score（is，Salimans et al（2016），越高越好）、Precision（Prec.，Kynka¨anniemi et al（2019），越高越好）和Recall（Rec.，Kynka-anniemi等人（2019）。附录C中提供了额外的实验细节。

6.1. 训练一致性模型

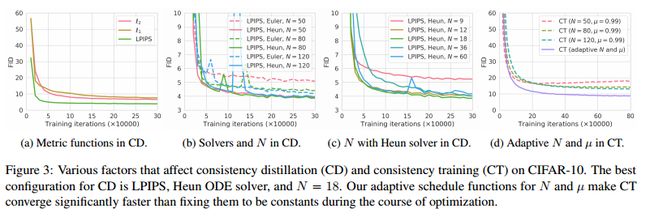
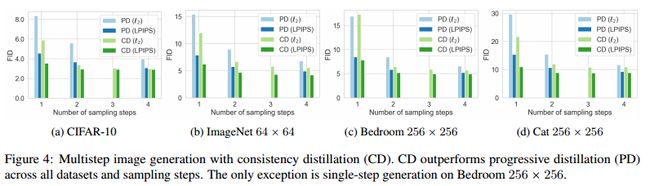
6.2. 少步骤图像生成

蒸馏

直接法生成

6.3. 零样本图像编辑

在附录D中，我们还演示了一致性模型在修复（图10）、插值（图11）和去噪（图12）方面的零样本能力，并提供了更多关于彩色化（图8）、超分辨率（图9）和stroke-guided图像生成（图13）的示例。

7. Conclusion

我们引入了一致性模型，这是一种专门为支持一步和少步骤生成而设计的生成模型。我们已经实证证明，我们的一致性蒸馏方法在多个图像基准和各种采样迭代上的扩散模型的现有蒸馏技术中相形见绌。此外，作为一个独立的生成模型，一致性模型优于其他允许单步生成的可用模型，排除了GANs。与扩散模型类似，它们还允许使用零样本图像编辑应用，如修复、着色、超分辨率、去噪、插值和stroke-guided图像生成。

此外，一致性模型与其他领域使用的技术有着惊人的相似之处，包括深度Q学习（Mnih等人，2015）和基于动量的对比学习（Grill等人，2020；He等人，2020）。这为这些不同领域的思想和方法的启发提供了令人兴奋的前景。

Appendices

Appendix A Proofs
A.1 Notations
A.2 Consistency Distillation
A.3 Consistency Training
Appendix B Continuous-Time Extensions
B.1 Consistency Distillation in Continuous Time
B.2 Consistency Training in Continuous Time
B.3 Experimental Verifications
Appendix C Additional Experimental Details
C.1 Model Architectures
C.2 Parameterization for Consistency Models
C.3 Schedule Functions for Consistency Training
C.4 Training Details
Appendix D Additional Results on Zero-Shot Image Editing
D.1 Inpainting
D.2 Colorization
D.3 Super-resolution
D.4 Stroke-guided image generation
D.5 Denoising
D.6 Interpolation
Appendix E Additional Samples from Consistency Models