Day2：有序数组的平方+最小子数组+螺旋矩阵II

一、有序数组的平方（977.）

题目建议： 本题关键在于理解双指针思想

题目链接：https://leetcode.cn/problems/squares-of-a-sorted-array/

文章讲解：https://programmercarl.com/0977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.html

视频讲解： https://www.bilibili.com/video/BV1QB4y1D7ep

方法1：暴力解法

时间复杂度：O($lo{g}_{2}n$)
空间复杂度：O(1)

class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        for i in range(len(nums)):
            nums[i] = nums[i] ** 2
        nums.sort() #排序函数
        return nums

方法2：双指针法

题目分析：给定的数组是递增的， 只是负数平方之后可能成为最大数了，因此数组平方的最大值必定来自数组的最左或最右元素。

双指针法：定义一个和原数组同样大小的辅助数组result，令k指向result数组终止位置，令i指向原数组起始位置，令j指向原数组终止位置。再把i和j指向元素平方的较大值交给k即可

时间复杂度：O(n)
空间复杂度：O(n)

class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        n = len(nums)
        result = [0] * n  # 将辅助数组初始化为0
        i = 0             # i指向原数组开头
        j = n - 1         # j指向原数组结尾
        k = n - 1         # k指向辅助数组结尾
        while k >= 0:
            if (nums[i] ** 2) >= (nums[j] ** 2):
                result[k] = nums[i] ** 2
                i += 1
            else:
                result[k] = nums[j] ** 2
                j -= 1
            k -= 1
        return result

二、长度最小的子数组（209.）

题目建议： 本题关键在于理解滑动窗口，这个滑动窗口看文字讲解 还挺难理解的，建议大家先看视频讲解。 拓展题目可以先不做。

题目链接：https://leetcode.cn/problems/minimum-size-subarray-sum/

文章讲解：https://programmercarl.com/0209.%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.html

视频讲解：https://www.bilibili.com/video/BV1tZ4y1q7XE

方法1：暴力解法

时间复杂度：O( $n^2$)
空间复杂度：O(1)

class Solution:
    def minSubArrayLen(self, s: int, nums: List[int]) -> int:
        n = len(nums)
        min_len = float('inf') # 将min_len初始化为正无穷大
        for i in range(n): # 外层循环用i来确定子数组的起始位置
            cur_sum = 0
            for j in range(i, n): # 内层循环用j来确定子数组的结束位置
                cur_sum += nums[j]
                if cur_sum >= s:
                    min_len = min(min_len, j - i + 1)
                    break # 找到从位置i开始的满足条件的最小连续子数组时，用break跳出内层循环
        if min_len != float('inf'):
            return min_len
        else:
            return 0

方法2：滑动窗口法

窗口：左右指针之间的连续子数组

右指针（j）：右指针就是for循环里的索引，会遍历数组

左指针（i）：如果当前窗口满足条件了（即子数组和≥s），为找到最小子数组，窗口就该缩小（即左指针右移），直到窗口值

时间复杂度：O( $n$ )
空间复杂度：O(1)

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        min_len = float('inf')
        cur_sum = 0
        i = 0
        for j in range(len(nums)):
            cur_sum += nums[j]
            while cur_sum >= target:
                min_len = min(min_len, j - i + 1)
                cur_sum -= nums[i]
                i += 1
        if min_len != float('inf'):
            return min_len
        else:
            return 0

三、螺旋矩阵II（59.）

题目建议： 本题关键还是在转圈的逻辑，在二分搜索中提到的区间定义，在这里又用上了。

题目链接：https://leetcode.cn/problems/spiral-matrix-ii/

文章讲解：https://programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html

视频讲解：https://www.bilibili.com/video/BV1SL4y1N7mV/

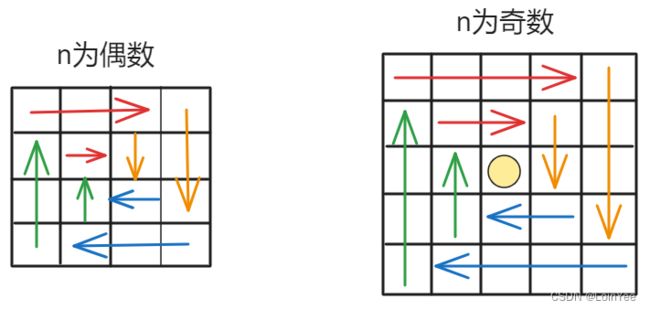
方法：模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

由外向内一圈一圈这么画下去，一共需要n//2次循环，每次循环起始点下标加一，终点下标减一

注意：要坚持左闭右开的循环不变量原则

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        nums = [[0] * n for _ in range(n)]  # 定义一个初始为0的二维数组
        startx, starty = 0, 0               # 起始点
        loop = n // 2                       # 循环次数
	      mid = n // 2                        # n为奇数时矩阵的中心点下标
				count = 1                           # 计数

        for offset in range(1, loop + 1) :       # 每循环一层偏移量加1，偏移量从1开始
            for i in range(starty, n - offset) :    # 从左至右，左闭右开
                nums[startx][i] = count
                count += 1
            for i in range(startx, n - offset) :    # 从上至下
                nums[i][n - offset] = count
                count += 1
            for i in range(n - offset, starty, -1) : # 从右至左
                nums[n - offset][i] = count
                count += 1
            for i in range(n - offset, startx, -1) : # 从下至上
                nums[i][starty] = count
                count += 1                
            startx += 1         # 更新起始点
            starty += 1

        if n % 2 != 0 :			# n为奇数时，填充中心点
            nums[mid][mid] = count 
        return nums