(每周10题)之 leetcode题目 ---(04~07)
写在前面的话,好多小伙伴们总是以刷题为目的,来提高自己,但是希望要灵活使用方法。可能我的观点有点不同,我觉得方法是循序渐进的,而不是一蹴而就出方法的,别人能想出方法的,也是一步一步考虑的,当我们看到别人的解决思路后,不是一味的记住,而是理解为何这样解决,还有中心的思想。
可能我观点比较幼稚,但是我依旧坚持我自己的想法,并加以实现。
第四题: 寻找两个正序数组的中位数
我的解题思路过程:看到题目后首先想到数据结构中并归算法,因为两个都是顺序的,通过并归排序后,通过判断总数是奇偶性质来找到中位数,初看题目,不就是那么简单吗,为啥是困难题目呢?我忽略了一点,要求时间复杂度为O(log(m + n))。而并归的算法的时间复杂度O(m+n),这个是不行的呀!
我陷入了思考,那我不并归呢,直接统计sum,找到第k大的数据不就可以了吗!都从第一个数据来判断,小的数据下标加1,直到找到中位数对应的下标,不就找到了吗,方法是可行,通过计算发现只是 O((m+n)/2)的复杂度,但是结果还是O(m+n),依旧不能,这题目。
题目给的时间复杂度其实也给了我们一个小提醒了,log类型,在log类中,二叉树中偏多,logN就是二叉树的高度,也是某些二叉树查找的次数,从第二个思考中,如果不采用从第一个位置来做比较,而是采用二分思想来找,每次找剩下的一半,这样就减少了查找的次数,而且也是log形式,于是写出了二分思想的查找.答案也就来了。
这个题目二分查找,我没有详细的解答,可以提供你去思考,可以参看代码去理解。
int findMedNum(const vector& nums1, const vector& nums2, int k)
{
int m = nums1.size();
int n = nums2.size();
int indexM = 0, indexN =0;
while (true)
{
// 边界情况
if (indexM == m)
{
return nums2[indexN + k -1];
}
if (indexN == n)
{
return nums1[indexM + k -1];
}
if (k == 1)
{
return min(nums1[indexM], nums2[indexN]);
}
//正常情况
int newIndexM = min(indexM +k/2-1,m-1);
int newIndexN = min(indexN +k/2-1,n-1);
if (nums1[newIndexM] <= nums2[newIndexN])
{
k -= newIndexM - indexM + 1;
indexM = newIndexM + 1;
}
else
{
k -= newIndexN - indexN + 1;
indexN = newIndexN + 1;
}
}
}
double findMedianSortedArrays(vector& nums1, vector& nums2)
{
int sumLength = nums1.size() + nums2.size(); //判断总数
if ( (sumLength & 0x01) == 1) //当为奇数
{
return findMedNum(nums1, nums2,(sumLength+1)/2);
}
else //为偶数时候
{
return (findMedNum(nums1, nums2, sumLength / 2) + findMedNum(nums1, nums2, sumLength / 2 + 1)) / 2.0;
}
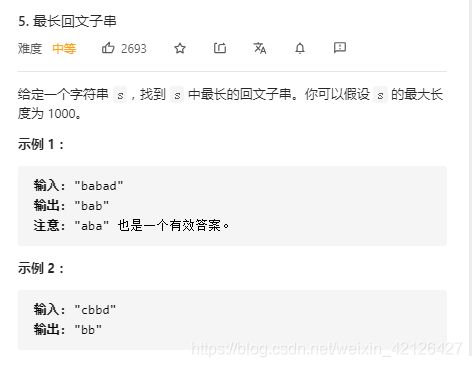
} 第五题:最长回文子串
解题想法,回文数是对称的,可以以一个数为中心,或者两个数的间隙为中心,向外扩散去找,记录找到的最大汇文长度的字符串,我第一想到的是这个,时间复杂度是O(N^2),也想到了采用暴力法来解决(时间复杂度是O(N^3)),还不如这个方法。于是采用了这个方式来写的代码:注:这个题目我自己写过代码,发现写的不够精简,于是采用了解答比较精炼的代码,
string centerSpread(string s, int left, int right) {
// left = right 的时候,此时回文中心是一个空隙,向两边扩散得到的回文子串的长度是奇数
// right = left + 1 的时候,此时回文中心是一个字符,向两边扩散得到的回文子串的长度是偶数
int size = s.size();
int i = left;
int j = right;
while (i >= 0 && j < size) {
if (s[i] == s[j]) {
i--;
j++;
}
else {
break;
}
}
// 这里要小心,跳出 while 循环时,恰好满足 s.charAt(i) != s.charAt(j),因此不能取 i,不能取 j
return s.substr(i + 1, j - i - 1);
}
string longestPalindrome(string s)
{
// 特判
int size = s.size();
if (size < 2) {
return s;
}
int maxLen = 1;
string res = s.substr(0, 1);
// 中心位置枚举到 len - 2 即可
for (int i = 0; i < size - 1; i++) {
string oddStr = centerSpread(s, i, i);
string evenStr = centerSpread(s, i, i + 1);
string maxLenStr = oddStr.size() > evenStr.size() ? oddStr : evenStr;
if (maxLenStr.length() > maxLen) {
maxLen = maxLenStr.size();
res = maxLenStr;
}
}
return res;
}
虽然通过了方法,但是后来了解到了Manacher 算法,这个算法使得题目降低到O(N),变成了线程。
代码作者连接,与Manacher 算法:
https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-dong-tai-gui-hua-by-liweiwei1419/
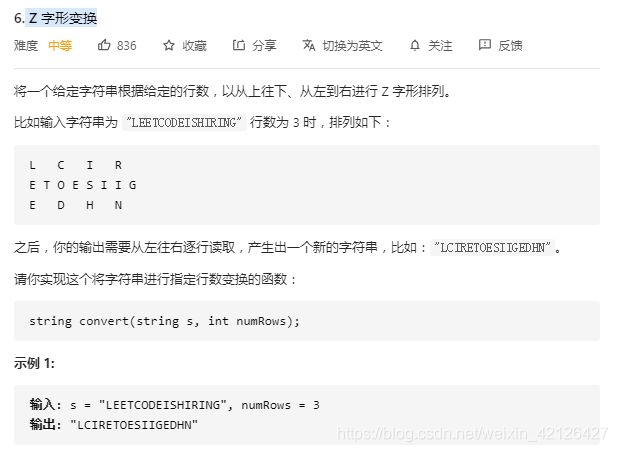
第六题:Z 字形变换
我的解题想法,拿到题目后,我当然想到不能去变换,这个题目可以说是很有意思了,有点规律性,比如numRows为n时,n-1的下标就是就是Z形状的角,每个元素都是关于角对称的,因此每一行数据都是固定的,只要遍历一遍,便可以得到答案,时间复杂度是O(n).
string convert(string s, int numRows)
{
int length = s.size();
if (length <= numRows || numRows ==1) //当小与等于numRows,结果就是源string
{
return s;
}
int index = numRows - 1; //下标减一
string str = "";
for (int i = 0; i<= index;i++)
{
int cur = i;
for (int j = 0; j= length)
{
break;
}
str += s[cur];
}
}
}
return str;
}
void testconvert()
{
string str1 = "PAYPALISHIRING";
string str = convert(str1, 3);
cout << "the ans is : " << str << endl;
} 输出结果:
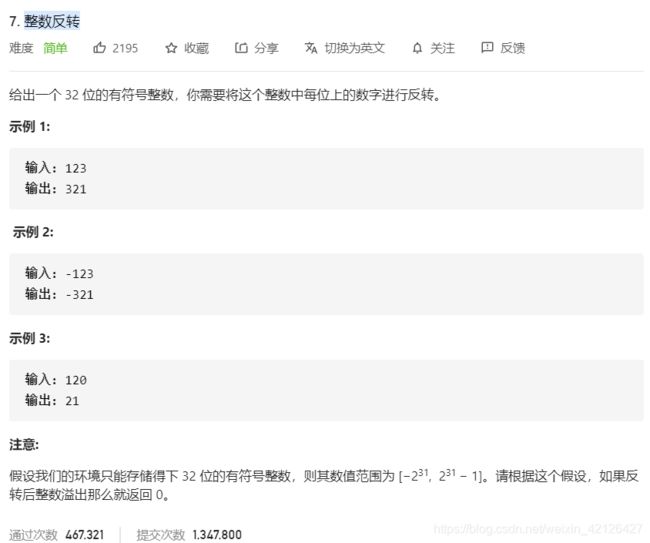
the ans is : PAHNAPLSIIGYIR第7题:整数反转
解题思路:就是普通的换位子,只是考虑一下溢出的问题:
int reverse(int x) {
int y = 0;
while (x != 0) {
int pop = x % 10;
x = x / 10;
if (y > INT_MAX / 10 || (y == INT_MAX / 10 && pop > 7))return 0;
if (y < INT_MIN / 10 || (y == INT_MIN / 10 && pop < -8)) return 0;
y = y * 10 + pop;
}
return y;
}就是那么简单,上面就是我对这些题的简单记录与看法,当然我自己写的代码肯定不会那么精简,希望更多朋友提出来。