1820:【00NOIP提高组】进制转换
我们可以用这样的方式来表示一个十进制数:将每个阿拉伯数字乘以一个以该数字所 处位置的(值减1)为指数,以10为底数的幂之和的形式。例如,123可表示为1*10^2+2*10^1 +3*10^0这样的形式。
与之相似的,对二进制数来说,也可表示成每个二进制数码乘以一个以该数字所处位 置的(值-1)为指数,以2为底数的幂之和的形式。一般说来,任何一个正整数R或一个负整数-R都可以被选来作为一个数制系统的基数。如果是以R或-R为基数,则需要用到的数码为0,1,....R-1。例如,当R=7时,所需用到的数码是0,1,2, 3,4,5和6,这与其是R或-R无关。如果作为基数的数绝对值超过10,则为了表 示这些数码,通常使用英文字母来表示那些大于9的数码。例如对16进制数来说,用A 表示10,用B表示11,用C表示12,用D表示13,用E表示14,用F表示15。 在负进制数中是用-R作为基数,例如-15(+进制)相当于110001(-2进制),
并且它可以被表示为2的幂级数的和数: 110001=1*(-2)^5+1*(-2)^4+0*(-2)^3+0*(-2)^2+0*(-2)^1+1*(-2)^0
问题求解:
设计一个程序,读入一个十进制数的基数和一个负进制数的基数,并将此十进制数转换为此负进制下的数:-R∈{-2,-3,-4,....-20}
#include
#include
#include
const int N=100;
int n,m;
int a[N];
char sa[10]={'A','B','C','D','E','F','G','H','I','J'};
int main()
{
scanf("%d%d",&n,&m);
int tot=0;
while(n!=0)
{
a[++tot]=n%m;
n/=m;
if(a[tot]<0) a[tot]-=m,n++;
}
for(int i=tot;i>=1;i--)
{
if(a[i]<10) printf("%d",a[i]);
else printf("%c",sa[a[i]-10]);
}
}
1821:【00NOIP提高组】乘积最大
今年是国际数学联盟确定的“2000——世界数学年”,又恰逢我国著名数学家华罗庚先 生诞辰90周年。在华罗庚先生的家乡江苏金坛,组织了一场别开生面的数学智力竞赛的活动,你的一个好朋友XZ也有幸得以参加。活动中,主持人给所有参加活动的选手出了这样一道题目:
设有一个长度N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积能够为最大。
同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子:
有一个数字串: 312,当N=3,K=1时会有以下两种分法:
1)3*12=36
2)31*2=62
这时,符合题目要求的结果是: 31*2=62
现在,请你帮助你的好朋友XZ设计一个程序,求得正确的答案。
#include
#include
#include
using namespace std;
long long g[20][50];
long long G(int x,int len,long long num)
{
if(g[x][len]) return g[x][len];
if(x==0) return g[x][len]=num;
for(int i=x-1;i
1822:【00NOIP提高组】单词接龙
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们己知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙" 中出现两次),在两个单词相连时,其重合部分合为一部分,例如beast和astonish,如果接成一条龙则变为beastonish,另外相邻的两部分不能存在包含关系,例如at和atide间不能相连。
#include
using namespace std;
string s[42];
int n, ans, vis[42];
int check(string x, string y){
int ans = -1;
int lenx = x.size();
int leny = y.size();
string t = "";
for(int i=0; i ans)
ans = len;
for(int i=1; i<=2*n; i++){
int pos = check(s[dep], s[i]);
int lenx = s[i].size();
if(pos != -1 && vis[i] == 0){
vis[i] = 1;
lenx = lenx - pos;
dg(i, len+lenx);
vis[i] = 0;
}
}
}
int main(){
cin >> n;
for(int i=1; i<=n; i++)
cin >> s[i];
for(int i=n+1; i<=2*n; i++)
s[i] = s[i-n];
cin >> s[0];
dg(0, 1);
cout << ans;
return 0;
}
1823:【00NOIP提高组】方格取数
设有N*N的方格图(N<=10),我们将其中的某些方格中填入正整数,而其他的方格中则放人数字0。如下图所示(见样例):
某人从图的左上角的A点出发,可以向下行走,也可以向右走,直到到达右下角的B点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从A点到B点共走两次,试找出2条这样的路径,使得取得的数之和为最大。

#include
#include
int max(int a,int b) {return a>b?a:b;}
/* dp[y1][x1][y2][x2] (x1<=x2) = max{
a[y1][x1] + a[y2][x2] + max{dp[y1-1][x1][y2-1][x2], dp[y1][x1-1][y2][x2-1], dp[y1-1][x1][y2][x2-1], dp[y1][x1-1][y2-1][x2]} (if (y1,x1) != (y2, x2)).
a[y1][x1] + max{...same with above}
}
*/
const int dir[2][2]={{1,0},{0,1}};
int main()
{
// load data
int n;
while (1==scanf("%d", &n))
{
int a[10][10];
int dp[10][10][10][10];
int x,y,num;
memset(a,0,sizeof(a));
memset(dp,-1,sizeof(dp));
while (3==scanf("%d%d%d",&y,&x,&num) && (x>=1 && y>=1))
{
a[y][x]=num;
}
dp[1][1][1][1]=a[1][1];
for (int round=1;round<2*n;round++)
{
//printf("round %d\n", round);
if (round==1) continue;
// (x, y) | x+y == round+1
for (int x1=1;x1<=n;x1++)
{
int y1=round+1-x1;
if (y1>=1 && y1<=n)
{
for (int x2=x1;x2<=n;x2++)
{
int y2=round+1-x2;
if (y2>=1 && y2<=n)
{
//printf("(y1,x1),(y2,x2): (%d,%d) (%d,%d)\n",y1,x1,y2,x2);
for (int z1=0;z1<2;z1++)
{
for (int z2=0;z2<2;z2++)
{
if (y1-dir[z1][0]>=1 && x1-dir[z1][1]>=1 && y2-dir[z2][0]>=1 && x2-dir[z2][1]>=1)
{
int tmp = dp[y1-dir[z1][0]][x1-dir[z1][1]][y2-dir[z2][0]][x2-dir[z2][1]];
if (tmp == -1) continue; // unreachable state
dp[y1][x1][y2][x2] = max(dp[y1][x1][y2][x2], tmp + a[y1][x1] + (x1!=x2?a[y2][x2]:0));
}
}
}
}
}
}
}
}
printf("%d\n",dp[n][n][n][n]);
}
return 0;
}
1824:【01NOIP提高组】一元三次方程求解
有形如:ax3+bx2+cx+d=0 这样的一个一元三次方程。给出该方程中各项的系数(a,b,c,d 均为实数),并约定该方程存在三个不同实根(根的范围在-100至100之间),且根与根之差的绝对值>=1。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后2位。
提示:记方程f(x)=0,若存在2个数x1和x2,且x1<x2,f(x1)*f(x2)<0,则在(x1,x2)之间一定有一个根。
#include
#include
double a,b,c,d;
double f(double x){
int i;
double ans=0;
double y;
y=1;
for(i=1;i<=3;i++)
y*=x;
y*=a;
ans+=y;
y=1;
for(i=1;i<=2;i++)
y*=x;
y*=b;
ans+=y;
y=1;
y*=x;
y*=c;
ans+=y;
ans+=d;
return ans;
}
int main(){
double x,x1,x2,x3;
scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
x=-100;
while(x-100<=0.000001){
if(fabs(f(x))<=0.000001)
break;
x+=0.01;
}
x1=x;
x+=0.01;
while(x-100<=0.000001){
if(fabs(f(x))<=0.000001)
break;
x+=0.01;
}
x2=x;
x+=0.01;
while(x-100<=0.000001){
if(fabs(f(x))<0.000001)
break;
x+=0.01;
}
x3=x;
printf("%.2lf %.2lf %.2lf\n",x1,x2,x3);
}
1825:【01NOIP提高组】数的划分
将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5; 1,5,1; 5,1,1;
问有多少种不同的分法。
#include
#include
using namespace std;
int f[210][210];
int main()
{
int n,k;
scanf("%d%d",&n,&k);
f[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=k;j++)
{
if(i>=j)f[i][j]=f[i-j][j]+f[i-1][j-1];
}
}
printf("%d\n",f[n][k]);
return 0;
}
1826:【01NOIP提高组】统计单词个数
给出一个长度不超过200的由小写英文字母组成的字母串(约定;该字串以每行20个字母的方式输入,且保证每行一定为20个)。要求将此字母串分成k份(1
#include
#include
#include
#include
#include
using namespace std;
int n,p,m;
char s[300],word[20][210];
int sa[300][300];
bool tf[300];
int f[300][300];
int main()
{
scanf("%d%d",&n,&p);
for(int i=0;i
#include
using namespace std;
const int maxn=105;
int n,s,t,A,B,T[maxn<<2];
double dis[maxn<<2];
bool book[maxn<<2];
struct data{
int city;
int x,y;
}a[maxn<<2];
inline int power_2(int x)
{
return x*x;
}
void getlast(int x1,int y1,int x2,int y2,int x3,int y3,int i)
{
int x4,y4;
int dis1=power_2(x1-x2)+power_2(y1-y2),
dis2=power_2(x1-x3)+power_2(y1-y3),
dis3=power_2(x2-x3)+power_2(y2-y3);
if(dis2==dis1+dis3) x4=x3-x2+x1,y4=y3+y1-y2;
if(dis1==dis2+dis3) x4=x2-x3+x1,y4=y2+y1-y3;
if(dis3==dis1+dis2) x4=x3-x1+x2,y4=y3+y2-y1;
a[i+3].x=x4;a[i+3].y=y4;
}
inline double distance(int x1,int y1,int x2,int y2)
{
return sqrt(power_2(x1-x2)+power_2(y1-y2));
}
void SPFA()
{
memset(book,0,sizeof(book));
queue q;
for(int i=1;i<=s<<2;i++) dis[i]=99999999;
for(int i=A*4-3;i<=A*4;i++) dis[i]=0,q.push(i),book[i]=1;
while(!q.empty())
{
int u=q.front();q.pop();book[u]=0;
for(int i=1;i<=s<<2;i++)
{
if(i==u) continue;
double cost=distance(a[i].x,a[i].y,a[u].x,a[u].y);
if(a[i].city==a[u].city) cost*=T[a[i].city];
else cost*=t;
if(dis[i]>dis[u]+cost)
{
dis[i]=dis[u]+cost;
if(!book[i])
{
book[i]=1;
q.push(i);
}
}
}
}
}
void init()
{
//memset(t,0,sizeof(t));
memset(a,0,sizeof(a));
scanf("%d%d%d%d",&s,&t,&A,&B);
int i;
for(i=1;i<=s<<2;i+=4)
{
//int x1,x2,x3,y1,y2,y3;
scanf("%d%d%d%d%d%d%d",&a[i].x,&a[i].y,&a[i+1].x,&a[i+1].y,&a[i+2].x,&a[i+2].y,&T[i/4+1]);
a[i].city=a[i+1].city=a[i+2].city=a[i+3].city=i/4+1;
getlast(a[i].x,a[i].y,a[i+1].x,a[i+1].y,a[i+2].x,a[i+2].y,i);
}
}
int main()
{
scanf("%d",&n);
int i;
for(i=1;i<=n;i++)
{
init();
SPFA();
double ans=dis[B<<2];
for(int j=B*4-3;jdis[j]) ans=dis[j];
printf("%.2lf\n",ans);
}
return 0;
}
1828:【02NOIP提高组】均分纸牌
有N堆纸牌,编号分别是1,2,3,...N。每堆上有若干张,但纸牌总数必为N的倍数。可以在任一堆上取若干张纸牌,然后移动。移牌规则为:在编号为1的堆上取的纸牌,只能移到编号为2的堆上;在编号为N的堆上取的牌只能移到编号为N-1的堆上;其余堆上取的纸牌,可以移到相邻左边或右边的堆上。现在要求找出一种移动方法,用最少的移动次数使每堆纸牌数都一样多。例如N=4,4堆纸牌数分别为:
①9 ②8 ③17 ④6
移动3次可达到目的:从 ③取4张牌放到④(9 8 13 10)-->从③取3张牌放到②(9 11 10 10)-->从②取1张牌放到 ①(10 10 10 10)。
#include
using namespace std;
const int maxn=105;
int n,sum,a[maxn];
int main()
{
int i,j,step=0;
cin>>n;
for(i=1;i<=n;i++)scanf("%d",&a[i]),sum+=a[i];
sum/=n;
for(i=1;i<=n;i++) a[i]-=sum;
i=1;
while(i1&&a[j]==0) j--;
while(i
1829:【02NOIP提高组】自由落体
在高为H的天花板上有n个小球,体积不计,位置分别为0,1,2,...。在地面上有一个小车(长为L,高为K,距原点距离为S1)。已知小球下落距离计算公式为s=1/2*g*t2,其中g=10,t为下落时间。地面上的小车以速度V前进。如图:
小车与所有小球同时开始运动,当小球距小车的距离≤0.00001时,即认为小球被小车接受(小球落到地面后不能被接受)。请你计算出小车能接受到多少个小球。

#include
#include
#include
#include
#include
#define eps 1e-5
#define rps 1e-6
using namespace std;
double H,S1,V,L,K;
int n;
int main()
{
scanf("%lf%lf%lf%lf%lf%d",&H,&S1,&V,&L,&K,&n);
double yu=S1-sqrt(H/5.0)*V-eps;int p=(int)yu;
if(yu-p>rps) p++;
double y=H-K-sqrt(eps);y=max(0.0,y);
y=S1+L-sqrt(y/5.0)*V+eps;int q=(int)y;
p=max(p,0);q=min(n-1,q);
printf("%d",max(0,q-p+1));
}
1830:【02NOIP提高组】矩形覆盖
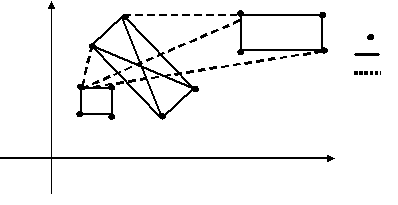
在平面上有n个点(n≤100),每个点用一对整数坐标来表示。例如:当n=4时,4个点的坐标分别为:P1(1,1),P2(2,2),P3(6,3),P4(7,0)
这些点可以用k个矩形(k<4)全部覆盖,矩形的边平行于坐标轴。如图一,当k=2是,可用如图二的两个矩形s1,s2覆盖,s1,s2面积和为4。问题是当n个点坐标和k给出后,怎样才能使得覆盖所有点的k个矩形的面积之和为最小呢。约定:
◇ 覆盖一个点的矩形面积为0;
◇ 覆盖平行于坐标轴直线上点的矩形面积也为0;
◇ 各个矩形间必须完全分开(边线也不能重合);
#include
#include
#include
#include
#define inf 99999999
using namespace std;
int n,k,ans=inf;
struct dot
{
int x,y;
}d[51];
struct sqr
{
dot l,r;
}rec[5];
bool conf(int i,int j)
{
if (rec[i].l.x==inf||rec[i].l.y==inf||rec[i].r.x==-inf||rec[i].r.y==-inf)
return 0;
if (rec[j].l.x==inf||rec[j].l.y==inf||rec[j].r.x==-inf||rec[j].r.y==-inf)
return 0;
if (rec[i].l.x>rec[j].r.x||rec[i].l.y>rec[j].r.y) return 0;
if (rec[j].l.x>rec[i].r.x||rec[j].l.y>rec[i].r.y) return 0;
return 1;
}
bool can()
{
for(int i=1;i<=k;i++)
for(int j=i+1;j<=k;j++)
if (conf(i,j)) return 0;
return 1;
}
int getS()
{
int S=0;
for(int i=1;i<=k;i++)
if (rec[i].l.x!=inf)
S+=(rec[i].r.x-rec[i].l.x)*(rec[i].r.y-rec[i].l.y);
return S;
}
void dfs(int used)
{
if (used==n)
{
int S=getS();
if (Sd[used+1].x) rec[i].l.x=d[used+1].x;
if (rec[i].l.y>d[used+1].y) rec[i].l.y=d[used+1].y;
if (rec[i].r.x


