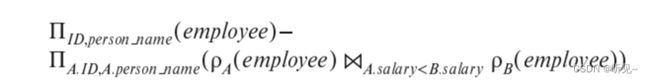数据库系统概念 第七版 中文答案 第2章 关系模型介绍
第2章 关系模型介绍
2.1 考虑图 2.17 中的员工数据库。这些关系上适当的主码是什么?
Answer:
相应的主键如下所示:
2.2 考虑从 instructor 的 dept_name 属性到 department 关系的外键约束。请给出对这些关系的插入和删除的示例,使得它们破坏该外码约束。
Answer:
- 插入元组:
(10111, Ostrom, Economics, 110000)
对instructor表插入,其中 department 表没有Economics,将违反外键约束。
- 删除元组:
(Biology, Watson, 90000)
从 department 表中,如果至少有一个student或 instructor 元组的 dept 名称 为 Biology,则会违反外键约束。
2.3 考虑 time_slot 关系。假设一个特定的时间片可以在一周之内出现不止一次,请解释为什么 day 和 start_time 是这种关系的主码的一部分,而结束则不是。
Answer:
属性 day 和 start_time 是主键的一部分,因为一个特定的课程很可能会在不同的天数上课,甚至可能在一天内上多次课。然而, end_time 不是主键的一部分,因为一个特定时间和特定日期开始的课程不能在多个时间结束。
2.4 在图2.1中所示的instructor实例中,没有两位教师具有相同的姓名。由此可推断,姓名可以作为教师的超键(或主键)吗?
Answer:
不是的。对于教师表的这种可能情况,姓名是唯一的,但一般情况下可能并不总是这样(除非大学规定两位教师不能有相同的姓名,这是一个相当不太可能的场景)。.
2.5 首先执行"student"和"advisor"关系的笛卡尔积,然后根据谓词"s_id = ID"对结果执行选择操作,最后的结果是什么?(在关系代数的符号表示中,这个查询可以写成:σ(s_id = ID) (student ⨝ advisor))
Answer:
结果中包含所有student属性的值,后跟所有advisor的属性。
对于每个有advisor的学生,结果都有一行该嘘声的属性,后跟一个s_id,该属性与学生的id属性相同,然后是i_id。
没有advisor 的学生不会出现在结果中。
有多个advisor的属性将在结果中出现相应从次数
2.6 考虑图2.17的员工数据库。为以下每个查询提供一个关系代数表达式。:
a. 找到居住在城市“Miami”的每个员工的名字.
b. 找到每个工资大于$100,000的员工的名字
c. 找到每个居住在“Miami”并且工资大于$100,000的员工的名字。
Answer:
2.7 考虑图2.18的银行数据库。为以下每个查询提供一个关系代数表达式。
a. 找到位于“Chicago”的每个分行的名称。.
b. 找到在分行“Downtown”有贷款的每个借款人的ID。
Answer:
2.8 请提出以下每个查询的关系代数表达式,考虑图2.17的员工数据库。
a. 找到每个不在“BigBank”工作的员工的ID和姓名。
b. 请找出至少与数据库中每位职员的薪水同样多的所有职员的ID和姓名。.
Answer:
a.要找到不在BigBank工作的员工,首先找到所有在BigBank工作的员工。这正是不在期望结果中的员工。然后,我们使用集合差异找到所有员工的集合减去不应在结果中的那些员工。
b. 我们使用与第一部分相同的方法,首先找到那些没有获得最高工资的员工,或者换句话说,有其他员工获得更多工资的员工。由于这涉及比较两个员工的工资值,我们需要两次引用员工关系,因此需要使用重命名。.
2.9 关系代数的除法运算符“÷”的定义如下。设r(R)和s(S)代表关系,且S ⊆ R,即模式S的每个属性也在模式R中。给定一个元组t,令t[S]表示元组t在S属性上的投影。然后r ÷s 是在模式 R - S上的关系(即在包含模式R中所有不在模式 S中的属性)。元组t在r ÷ s中当且仅当满足两个条件:
以上设计:
a. 使用除法运算符编写关系代数表达式,找到所有已经修读所有计算机科学课程的学生的ID。(提示:使用投影操作选择仅包含ID和课程ID的元组,并使用选择表达式生成所有计算机科学课程ID的集合,然后进行除法运算。)
b. 展示如何在关系代数中编写上述查询,而不使用除法运算符。(通过这样做,您将展示如何使用其他关系代数操作来定义除法运算。)
Answer: