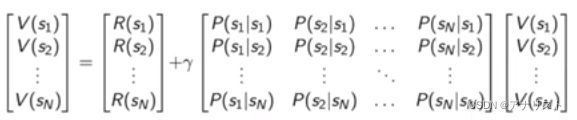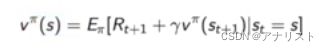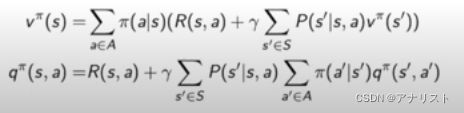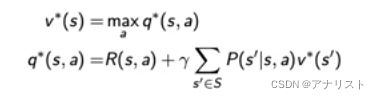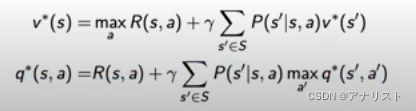马尔科夫决策过程(Markov Decision Process)揭秘
RL基本框架、MDP概念
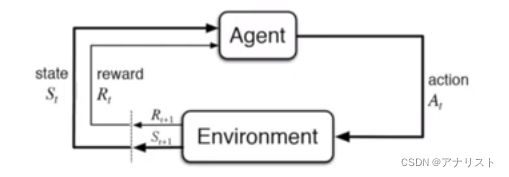
MDP是强化学习的基础。MDP能建模一系列真实世界的问题,它在形式上描述了强化学习的框架。RL的交互过程就是通过MDP表示的。RL中Agent对Environment做出一个动作(Action),Environment给Agent一个反馈(Reward),同时Agent从原状态(![]() )变为新状态(
)变为新状态(![]() )。这里的反馈可以是正、负反馈;Agent执行动作是根据某个策略(Policy)进行的。
)。这里的反馈可以是正、负反馈;Agent执行动作是根据某个策略(Policy)进行的。
可以看到,强化学习和传统机器学习的区别是 , 它不能立即得到标记,而只能得到一个暂时的反馈(多为人为经验设定)。因此可以说强化学习是一种标记延迟的监督学习 。
思考:MDP中,Environment是全部可观测的,部分可观测问题也能转化为MDP,如何理解?
Markov Property
假设状态的历史序列:![]() ={
={![]() ,
, ![]() , ...
, ... ![]() },状态
},状态![]() 具有马尔科夫性,当且仅当
具有马尔科夫性,当且仅当
p(![]() |
|![]() )=p(
)=p(![]() |
|![]() ),即“当给定现在(present),未来(future)独立于过去(past)”。
),即“当给定现在(present),未来(future)独立于过去(past)”。
换言之,马尔科夫性是指不具备记忆特质。未来的状态与任何历史的状态无关,仅与当前状态相关。
Markov Chain
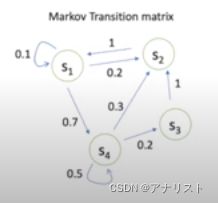
马尔科夫链(Markov Chain)和马尔科夫过程(Markov Process)基本等价。(具备离散状态的马尔可夫过程,通常被称为马尔可夫链)。例如下图中有4个状态,箭头表示状态转移,数字表示转移概率。从一个节点出发的概率之和为1.
我们将状态转移矩阵用P表示,其中每个元素为p(![]() =
=![]() |
|![]() =
=![]() ):
):
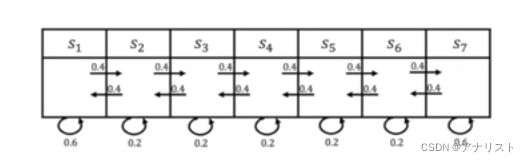
同样P的每一行之和为1.举一个具体例子:
上图的马尔科夫过程(MP)有7个状态,图中标出了每个状态去相邻状态或保留原地的概率。从![]() 出发的采样转移结果可能为:1)
出发的采样转移结果可能为:1) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 2)
2) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 3)
3) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等等,可以说马尔科夫过程(Markov process)是一个具备了马尔科夫性质的随机过程。
等等,可以说马尔科夫过程(Markov process)是一个具备了马尔科夫性质的随机过程。
马尔科夫奖励过程(MRP)
MRP等于Markov Chain加上奖励,即MRP=Markov Chain+Reward。其中奖励函数(Reward function)是关键,R(![]() =
=![]() )=E[
)=E[![]() |
|![]() =s]。
=s]。
现在,针对上述例子,把奖励放进去,假设![]() 对应奖励为+5,
对应奖励为+5,![]() 对应奖励为+10,其余状态奖励为0,我们得到R的向量为:[5,0,0,0,0,0,10]。
对应奖励为+10,其余状态奖励为0,我们得到R的向量为:[5,0,0,0,0,0,10]。
值函数(Value Function)
首先定义反馈值的折扣求和(Discounted sum),其中![]() ,
,![]()
再定义值函数,![]() =E[
=E[![]() |
|![]() =s]=E[
=s]=E[![]() |
|![]() =s],表示从t时刻开始的未来的奖励。
=s],表示从t时刻开始的未来的奖励。
为啥需要折扣因子![]() ?
?
1. 避免在循环MRP中返回无限大的反馈值
2. 对未来的不确定性需要被完全表示出来
3. 有一层类似金融背景的含义:即时的反馈总是能赚取比延迟反馈更多的利益;对人类来说,更倾向于即时反馈
4. 若使用没有折扣的MRP,如![]() =1,那么未来的反馈值就等于即时的反馈值;如
=1,那么未来的反馈值就等于即时的反馈值;如![]() =0,那么相当于只关心即时的反馈值
=0,那么相当于只关心即时的反馈值
MRP的奖励计算举例
取![]() =0.5,那么上图中,对于采样路径
=0.5,那么上图中,对于采样路径![]() ,
,![]() ,
,![]() ,
,![]() 的奖励值是:0+0.5*0 +0.25*0 + 0.125*10 =1.25;对于采样路径
的奖励值是:0+0.5*0 +0.25*0 + 0.125*10 =1.25;对于采样路径![]() ,
,![]() ,
,![]() ,
,![]() 的奖励值是:0+0.5*0 +0.25*0+ 0.125*5=0.625;对于采样路径
的奖励值是:0+0.5*0 +0.25*0+ 0.125*5=0.625;对于采样路径![]() ,
,![]() ,
,![]() ,
,![]() 的奖励值是:0
的奖励值是:0
值函数的计算
利用Bellman equation(贝尔曼方程),即
V(s)包括两部分,即时奖励和未来奖励的折扣求和。
它的另一种表达方式是:
Bellman equation描述了状态(或状态的值)的迭代关系,举例说明:
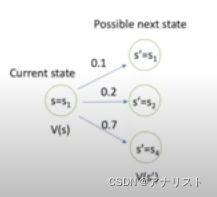
假如有以下状态和状态转移矩阵(下图左),那么对于![]() 状态,它和它的下一个状态
状态,它和它的下一个状态![]() 、
、![]() 、
、![]() 的状态转移关系和值迭代关系如下图右所示。
的状态转移关系和值迭代关系如下图右所示。
Bellman equation也可以写成矩阵的形式,
即在MRP中,![]() ,以及
,以及![]()
因为矩阵的逆求解复杂度为![]() ,其中N为状态数。因此直接线性代数求解只适用于较小规模的MRP问题。
,其中N为状态数。因此直接线性代数求解只适用于较小规模的MRP问题。
真正通用的求解方法是迭代算法,如动态规划算法(DP)、蒙特卡洛算法(MC)、时序差分算法(TD)。其中MC和TD都是无模型强化学习,适用于不知道概率转移情况的模型, 但要注意,无模型强化学习并不代表不能被MDP描述, 而是指其中的参数是未知的。
蒙特卡洛算法(MC)
MC用“采样”代替直接的策略评估,然后求平均累积奖励,作为期望累积奖励。关于某个状态的奖励返回的经验样本越多,能够得到的平均奖励值就越接近于期望的状态奖励值,井且收敛于这个值。具体如下
以下算法是等价的:
对于前面例子中![]() 的反馈值V(
的反馈值V(![]() ),可能有如下采样过程和奖励返回值,从而计算平均值:
),可能有如下采样过程和奖励返回值,从而计算平均值:
对于采样路径![]() ,
,![]() ,
,![]() ,
,![]() 的奖励值是:0+0.5*0 +0.25*0 + 0.125*10 =1.25;对于采样路径
的奖励值是:0+0.5*0 +0.25*0 + 0.125*10 =1.25;对于采样路径![]() ,
,![]() ,
,![]() ,
,![]() 的奖励值是:0+0.5*0 +0.25*0+ 0.125*5=0.625;对于采样路径
的奖励值是:0+0.5*0 +0.25*0+ 0.125*5=0.625;对于采样路径![]() ,
,![]() ,
,![]() ,
,![]() 的奖励值是:0,以此类推,最终求平均即可。
的奖励值是:0,以此类推,最终求平均即可。
动态规划算法(DP)
如果说MC是一种基于一个事件又一个事件的算法(Episode by Episode),那么DP就是一个基于动作选择的算法(Step-by-Step)。两者具有非常多的相似之处。具体如下
其中核心语句是第4行,即Bellman equation
Markov Decision Process (MDP)
MDP是带有决策的MRP,即MDP=MRP+actions或MDP=MRP+decisions。MDP一般用5元组表示,即(S,A,P,R,![]() )。其中S是有限状态的集合;A是有限动作的集合;P是状态转移矩阵,对于每个action,有P(
)。其中S是有限状态的集合;A是有限动作的集合;P是状态转移矩阵,对于每个action,有P(![]() =s'|
=s'|![]() =s,
=s,![]() =a);R是反馈函数(或奖励值函数),每个状态对应一个值或每个状态-动作对(State-Action)对应一个值,即R(
=a);R是反馈函数(或奖励值函数),每个状态对应一个值或每个状态-动作对(State-Action)对应一个值,即R(![]() =s,
=s,![]() =a)=E(
=a)=E(![]() |
|![]() =s,
=s,![]() =a);
=a);![]() 仍是折扣因子,
仍是折扣因子,![]() 。
。
MDP中策略(Policy)是指每个状态下应该执行什么动作,即它指定了动作的分布。策略表示为:![]() ,即它是与时间t无关的。对于任意的t>0,有
,即它是与时间t无关的。对于任意的t>0,有![]() ~
~![]()
MDP和MRP的转换
上图中,等式左边是MRP,等式右边是MDP;右边对动作a求和,消掉a,因此左边都没有a
MDP和MRP的比较
上图中,左边是MRP,右边是MDP;右边比左边多了一层a节点(黑色节点),表示动作;MRP直接从s状态映射(转移)到s'状态,而MDP先把状态s映射到动作a,通过![]() ,再把动作a和状态s的组合映射到新的状态s',通过P(s'|s,a);体现了MDP=MRP+actions
,再把动作a和状态s的组合映射到新的状态s',通过P(s'|s,a);体现了MDP=MRP+actions
MDP中的值函数
在策略![]() 下,状态s的值函数为:
下,状态s的值函数为:![]() ,表示在初始状态为s的情况下采取策略
,表示在初始状态为s的情况下采取策略![]() 得到的累积期望奖励值。动作值函数为:
得到的累积期望奖励值。动作值函数为:![]() ,二者的关系是:
,二者的关系是:
以上两式展开,变为迭代形式
这两公式叫Bellman Expectation Equation(贝尔曼期望方程)
思考:贝尔曼期望方程只是比贝尔曼方程多了个期望![]() ?
?
 和
和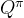 的关系
的关系
分别将![]() 的展开式插入
的展开式插入![]() 的公式,以及将
的公式,以及将![]() 的展开式插入
的展开式插入![]() 的公式得到更复杂的两个迭代式,如下
的公式得到更复杂的两个迭代式,如下
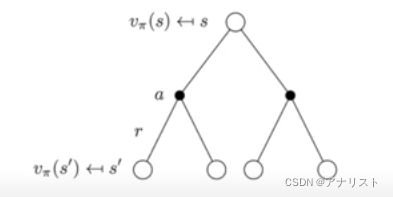
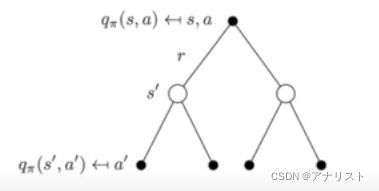
上式![]() 的含义可用一颗三层的树描述,根节点是要求的
的含义可用一颗三层的树描述,根节点是要求的![]() ,黑色节点是对所有动作求和,底层白色节点是对所有状态求和。
,黑色节点是对所有动作求和,底层白色节点是对所有状态求和。
类似的,![]() 也可以用一颗树描述,根节点是要求的
也可以用一颗树描述,根节点是要求的![]() ,中间白色节点是对所有状态求和,底层黑色节点是对所有动作求和。
,中间白色节点是对所有状态求和,底层黑色节点是对所有动作求和。
策略评估(Policy Evaluation)
首先关于MDP和MRP的区别,做一个形象的补充:MRP更像随波逐流,MDP更像有人掌舵;和前文说的MDP=MRP+actions一致。
策略评估是指,给定一个策略![]() ,求该策略下的值函数
,求该策略下的值函数![]() ,越大越好
,越大越好
下面举例说明策略评估的过程
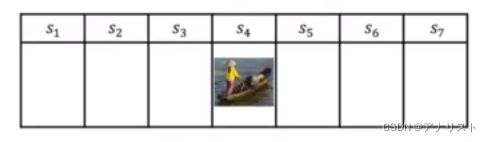
假设一艘船有两个方向,向左或向右,还是有7个状态,如图所示,在![]() 的奖励为+5,在
的奖励为+5,在![]() 的奖励为+10,其余奖励为0,因此有R=[5,0,0,0,0,0,10]
的奖励为+10,其余奖励为0,因此有R=[5,0,0,0,0,0,10]
当策略是一直往left,同时取![]() =0时,利用
=0时,利用
迭代计算,最终收敛得到![]() =[5,0,0,0,0,0,10]
=[5,0,0,0,0,0,10]
思考一:策略不变,同时取![]() =0.5时,得到的
=0.5时,得到的![]() 是多少?
是多少?
思考二:策略变为一半概率left,一半概率right(即P(![]() (s)=left)=0.5,P(
(s)=left)=0.5,P(![]() (s)=right)=0.5),同时取
(s)=right)=0.5),同时取![]() =0.5时,得到的
=0.5时,得到的![]() 是多少?
是多少?
上式也可以写为
策略搜索(Policy Search)
最优状态值函数![]() 对应一个最优策略,后者在所有策略中取得最大值函数,即
对应一个最优策略,后者在所有策略中取得最大值函数,即
![]()
而最优策略就是![]() 。当最优值被找到,就认为MDP被解决。一般认为只存在唯一的最优值函数,但可能会存在多个最优策略。
。当最优值被找到,就认为MDP被解决。一般认为只存在唯一的最优值函数,但可能会存在多个最优策略。
为了寻找最优策略,需要最大化![]() ,即
,即
对于任意MDP,总是存在确定性的最优策略;如果已知![]() ,就能立即得到最优策略
,就能立即得到最优策略
策略求解之策略迭代
策略迭代包括两个步骤:策略评估(在当前策略更新各个状态的值函数);策略更新(基于当前的值函数,采用![]() -贪心算法找到当前最优的策略),即
-贪心算法找到当前最优的策略),即![]()
迭代过程的形象化描述如上图。伪代码如下
思考:怎么证明策略一直在提升,且策略迭代一定能收敛?
最优值函数是在贝尔曼最优方程满足时达到的,即
上面两式互相插入,得到
策略求解之值迭代
值迭代也是将贝尔曼最优方程作为更新规则
在每一次值迭代中都能找到让当前值函数最大的更新方式, 并且用这种方式来更新值函数。不断更新迭代,直到值函数不再发生变化。完整伪代码如下
另一个等价的实现算法
思考:如何证明策略的改进和值函数的改进是一致的?
策略迭代和值迭代的对比
无论策略迭代还是值迭代,都属于动态规划算法。
策略迭代包括:策略评估 和 策略提升(或策略更新)
值迭代包括:找到最优值函数 和 策略抽取;这里不需要重复两个动作,因为一旦值函数是最优的,那么相应的策略就一定是最优的,也就是收敛了。所以你会发现,策略迭代的算法有两层loop,而值迭代的算法只有一层。
值迭代中寻找最优值函数也可以看成是一种策略提升(因为有个max操作)和 简化的策略评估的结合体(因为无论收敛与否,都只有一次v(s)的赋值)。
策略迭代更像是一种累计平均的计算方式,而值迭代更像是一种单步最好的方式。 从速度来说,值迭代更加迅速,特别是在策略空间较大的时候。从准确度来说,策略迭代更接近于样本的真实 分布。
MDP和RL扩展链接
https://github.com/ucla-rlcourse/RLexample/tree/master/MDP
REINFORCEjs: Gridworld with Dynamic Programming