二分查找(代码实现)

二分查找：

文章参考：二分查找(折半查找算法)
二分查找又称折半查找、二分搜索、折半搜索等，是在分治算法基础上设计出来的查找算法，对应的时间复杂度为O(logn)。
$二分查找算法仅适用于有序序列，它只能用在升序序列或者降序序列中查找目标元素。$

二分查找算法的实现思路

在有序序列中，使用二分查找算法搜索目标元素的核心思想是：不断地缩小搜索区域，降低查找目标元素的难度。

以在升序序列中查找目标元素为例，二分查找算法的实现思路是：
初始状态下，将整个序列作为搜索区域（假设为 [B, E]）；
找到搜索区域内的中间元素（假设所在位置为 M），和目标元素进行比对。如果相等，则搜索成功；如果中间元素大于目标元素，表明目标元素位于中间元素的左侧，将 [B, M-1] 作为新的搜素区域；反之，若中间元素小于目标元素，表明目标元素位于中间元素的右侧，将 [M+1, E] 作为新的搜素区域；
重复执行第二步，直至找到目标元素。如果搜索区域无法再缩小，且区域内不包含任何元素，表明整个序列中没有目标元素，查找失败。
举个简单的例子，在下图所示的升序序列中查找元素 31。

图 1 中，所有元素的位置分别用 0~9 表示，中间元素的位置为 ⌊ 0 + (9 - 0) / 2 ⌋ = 4，如下图所示：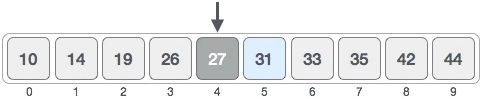

中间元素 27 < 31，可以断定 [0, 4] 区域内绝对没有 31，目标元素只可能位于 [5, 9] 区域内，如下图所示：

2. 在 [5, 9] 区域内，中间元素的位置为 ⌊ 5 + (9 - 5) / 2 ⌋ = 7，如下图所示：

中间元素 35 > 31，可以断定 [7, 9] 区域内绝对没有 31，目标元素只可能位于 [5,6] 中，如下图所示：

3. 在 [5, 6] 区域内，中间元素的位置为 ⌊ 5 + (6- 5) / 2 ⌋ = 5，中间元素就是 31，成功找到目标元素。

---

代码实现

C语言：

int search(int array[],int n,int target){
    int left = 0;
    int right = n-1;
    while(left<=right){
        int middle = left + ((right - left)>>1);//防止溢出。>>1为向右移一位，比除以2速度更快
        if(array[middle] > target){
            right = middle - 1;//target在左区间。
        }else if(array[middle] < target){
            left = middle + 1;//target在右区间。
        }else{
            return middle;//tarfet在中间。
        }
    }
    return -1;//没有找到该元素。
}

Java(简版):

import java.util.Scanner;
public class search {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        boolean judge = true;
        int[]array = new int[]{-22,-11,-1,0,11,22,33,44,55,66,77,88,99};
        int target = 23;
        int left = 0,right = array.length-1;
        while(left<=right){
            int middle = (left+right)/2;
            if(target==array[middle]){
                System.out.println("找到指定元素，位置为："+(middle+1));
                judge = false;
                break;
            }else if(array[middle]>target){
                right = middle - 1;
            } else if (array[middle]<target) {
                left = middle + 1;
            }
        }
        if(judge){
            System.out.println("很抱歉，没有找到该元素！");
        }
    }
}

Java(最终)：

//Java自带二分查找
//Java源码：
// Like public version, but without range checks.

/**
     * Checks that {@code fromIndex} and {@code toIndex} are in
     * the range and throws an exception if they aren't.
     */
static void rangeCheck(int arrayLength, int fromIndex, int toIndex) {
        if (fromIndex > toIndex) {
            throw new IllegalArgumentException(
                "fromIndex(" + fromIndex + ") > toIndex(" + toIndex + ")");
        }
        if (fromIndex < 0) {
            throw new ArrayIndexOutOfBoundsException(fromIndex);
        }
        if (toIndex > arrayLength) {
            throw new ArrayIndexOutOfBoundsException(toIndex);
        }
    }
public static int binarySearch(long[] a, int fromIndex, int toIndex,long key) {
    /**
     * Searches a range of
     * the specified array of longs for the specified value using the
     * binary search algorithm.
     * The range must be sorted (as
     * by the {@link #sort(long[], int, int)} method)
     * prior to making this call.  If it
     * is not sorted, the results are undefined.  If the range contains
     * multiple elements with the specified value, there is no guarantee which
     * one will be found.
     *
     * @param a the array to be searched
     * @param fromIndex the index of the first element (inclusive) to be
     *          searched
     * @param toIndex the index of the last element (exclusive) to be searched
     * @param key the value to be searched for
     * @return index of the search key, if it is contained in the array
     *         within the specified range;
     *         otherwise, (-(insertion point) - 1).  The
     *         insertion point is defined as the point at which the
     *         key would be inserted into the array: the index of the first
     *         element in the range greater than the key,
     *         or {@code toIndex} if all
     *         elements in the range are less than the specified key.  Note
     *         that this guarantees that the return value will be >= 0 if
     *         and only if the key is found.
     * @throws IllegalArgumentException
     *         if {@code fromIndex > toIndex}
     * @throws ArrayIndexOutOfBoundsException
     *         if {@code fromIndex < 0 or toIndex > a.length}
     * @since 1.6
     */
        rangeCheck(a.length, fromIndex, toIndex);
        return binarySearch0(a, fromIndex, toIndex, key);
    }
private static int binarySearch0(long[] a, int fromIndex, int toIndex,long key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        long midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

注：使用条件为该数组已升序(降序)排序且无重复元素。

时间复杂度：O(log2N)

空间复杂度：O(1)