「自控原理」4.1 根轨迹及其绘制

本节介绍根轨迹的概念及绘制方法
本节介绍广义根轨迹及其绘制方法

---

概述

根轨迹法是三大分析校正方法之一，是一种图解法。
根轨迹法适合研究当系统中某一参数变化时，系统性能的变化趋势。具有直观、形象的特点，但由于图解存在一定近似，因此不十分精确。

根轨迹法的基本概念

根轨迹：开环系统的某一参数从$0\to \infty$变化的时候，闭环系统特征根$\lambda$在s平面相应变化所描绘出来的轨迹。
使用系统开环传递函数以及根轨迹的绘制规则，可以得到闭环极点的位置及其变化趋势，进而分析系统的性能。
用一个例题来直观感受一下根轨迹法的基本概念：

在之前的文章中提到过根轨迹增益：
也就是把开环传递函数化成首一标准形式时的增益。化成首一是为了保证特征方程最高次系数为1，方便特征方程的求解。比如这道题里的K* 就是根轨迹增益。
当K从零到无穷变化，K* 也从零到无穷变化。
当$0<K^{\ast }\le 1$，两根为实数，且分别从0和-2向-1靠拢。
当$K^{\ast }>1$，两根为复数，实部不变，虚部随着K*的增大而增大，直到无穷。于是就有了之前这样的根轨迹。

那么这个根轨迹有什么用呢？从这个例子来说，通过选取增益K，可以使闭环极点落在根轨迹上的任何位置。如果根轨迹上某一点能够满足系统动态性能指标，那么可以通过计算这一点的参数K直接完成设计。（系统动态性能与闭环极点之间的关系可以参考3.2节

闭环零极点和开环零极点之间的关系

来看这个小例子：

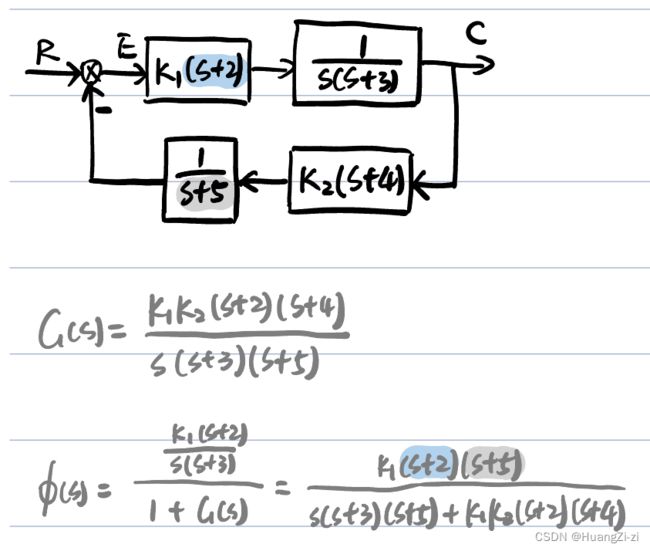
从这个化出来的传递函数来看，零点（分子为零）包含了前向通道的零点和反馈通道的极点
而极点（分母为零）和开环的零点、极点、两个增益（乘在一起就是根轨迹增益）都有关

闭环零点：前向通道开环零点 + 反馈通道开环极点
闭环极点：与开环零点、开环极点、根轨迹增益K*均有关

根轨迹方程

之前绘制根轨迹，比较盲目，因为只是单纯在图形角度进行了分析。但如果想要更加精确的计算，就需要引入代数的方程。也就是根轨迹图像对应的方程——根轨迹方程
看这个单位反馈系统：

这个蓝色底的方程就是根轨迹方程，它可以被分解成两个方程，分别表示矢量的模值和相角

回到一般情况：

这两个拆分出来的方程分别称为模值条件和相角条件

由于K*的的取值范围是$0\sim +\infty$，所以对于任意的s，模值条件都是可以满足的。
但是可以通过相角条件判断某一个点是否在根轨迹上。

$几点解释：$

1. 对于s平面上任何一个点，都能找到一个K*满足模值条件。（但是这个点不一定满足相角条件因此不一定在根轨迹上）
2. s平面上满足相角条件的点一定在根轨迹上。（满足相角条件是该点位于根轨迹上的充要条件）

根轨迹的绘制

逐点计算的方法绘制根轨迹很显然不适用于复杂情况。绘制根轨迹有一些基本法则。在精度要求不高的情况下可以利用这些法则快速、简便的画出根轨迹。

法则1：起点和终点

根轨迹起点：开环极点
根轨迹终点：开环零点
如果开环极点个数n大于开环零点个数m，则有n-m条根轨迹终止于无穷远处

法则2：分支数、对称性、连续性

根轨迹的分支数：开环极点数
根轨迹关于实轴对称
根轨迹连续

法则3：实轴上的根轨迹

从实轴上最右端的开环零点或极点算起（从1算起），奇数开环零极点到偶数开环零极点之间的区域是根轨迹

另外一种表述：某一区域右边开环零极点个数之和为奇数，则这一个区域为根轨迹

法则4：根之和

当开环极点数n和开环零点数m满足：$n-m\ge 2$
闭环根之和为一个常值

另一种表述：开环n个极点之和 = 闭环特征方程n个根之和

根之和为常数表明：当一条根轨迹向左，必然另外有一条根轨迹向右，以保证根轨迹上点之和为常数。

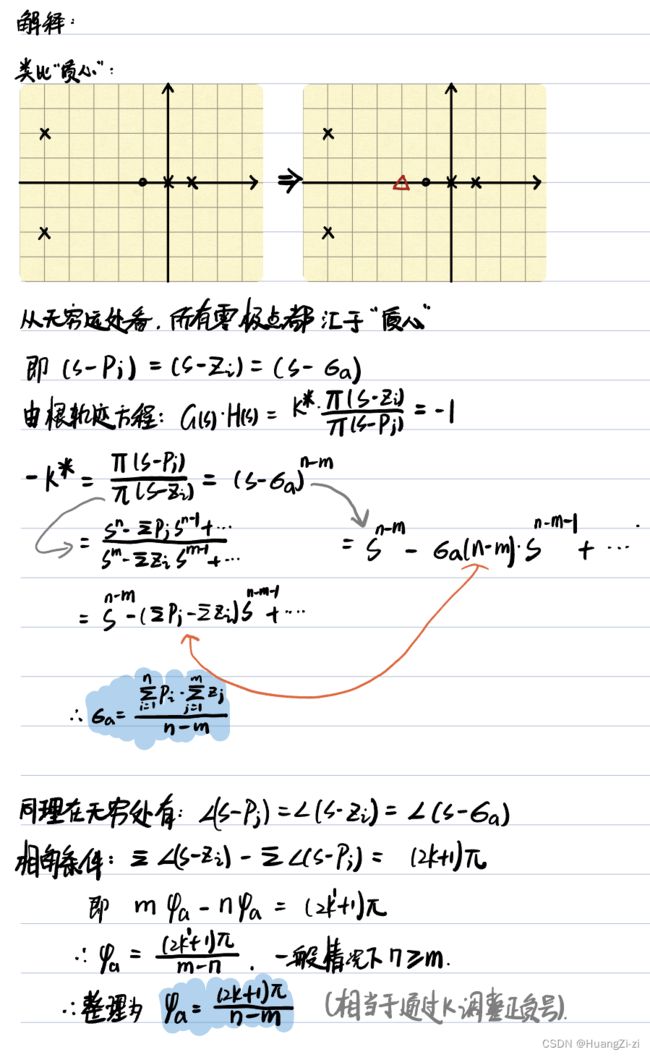
法则5：渐近线

$\{\begin{array}{rl}{\sigma }_a& =\frac{\sum _{i=1}^n{p}_i-\sum _{j=1}^n{z}_j}{n-m}\\ & \\ {\phi }_a& =\frac{(2k+1)\pi }{n-m}\end{array}$
开环极点数n>开环零点数m时，有n-m条根轨迹分支趋向无穷远。其渐近线为与实轴交角为${\phi }_a$，交点为${\sigma }_a$的一组直线。
根轨迹的渐近线反应了当n>m时，n-m条根轨迹趋于无穷处的规律

来看一道例题：

这里最后运用了根之和，正好前面没有举例题，借着这道题讲一下。三个开环极点，所以产生三个根轨迹分支。由实轴上的根轨迹已经可以判断其中一个分支了，一定从-4极点走向-2零点。剩下两个分支走向无穷，渐近线也算出来了。
从-1极点出来，没办法向左走（因为这边不是根轨迹），所以从-1出发的这一支一定向右。那么从0出发的这一支必然向左，保证三个根之和为定值。
-1出来和0出来的两支合并的点应该偏左，因为0向左走的需要抵消-4和-1两个向右走的。
合并之后-4继续向右，所以剩下两支就向左去趋近渐近线了。

法则6：分离点/会合点

$\sum _{i=1}^n\frac{1}{d-p_i}=\sum _{j=1}^m\frac{1}{d-z_j}$
分离点的本质就是当根沿着根轨迹移动的时候发生了重合，然后再分道扬镳。所以计算分离点也就是对应计算重根。
还是用之前这个例题：

代入极点、零点，就可以算出分离点d。在这道例题里面分离点是-0.55（按计算器解方程啦）
这个就不再单独举例题了。

分离点还有另外一种表述方式：
$\frac{\mathrm{d}K}{\mathrm{d}s}=0$，也就是在根轨迹方程里把K提出来变成s的函数，再求导，倒数等于0的点就是分离点\会合点

法则7：与虚轴的交点

如果根轨迹相交，那么交点就是系统的临界稳定点，可以用劳斯稳定性判据确定，也可以令闭环特征方程的$s=j\omega$，然后分别求解实部和虚部为零，解出交点。

核心的点就是从临界稳定这里切入解决问题。

法则8：出射角/入射角

同样也称作起始角/终止角
$\sum _{j=1}^m\angle (s-z_j)-\sum _{i=1}^n\angle (s-p_i)=(2k+1)\pi$
说白了就是相角条件
知道了出射角、入射角，就可以知道曲线一开始是向什么方向走的，有助于画出更准确的根轨迹。
一般来说不需要精确计算，只需要知道一个大概就可以了，所以这个就不单独举例题了。

除了以上法则以外，还有以下的两个定理可以辅助绘制根轨迹：

定理1：2极点1零点

如果系统有两个开环极点，一个开环零点，并且在复平面存在根轨迹，那么根轨迹一定是以这个零点为圆心的圆弧

注意两点：圆弧不一定是完整的，圆弧半径也有可能是0。
所以具体怎么画根轨迹还需要参考其他的法则。

定理2：根轨迹对称性

如果开环零、极点数均为偶数，并且关于一条平行于虚轴的直线左右对称，则根轨迹一定关于这条直线左右对称。

例题

看起来这样做是没有问题的，但是如果我们加入出射角这一项，再进行计算的话，就可以知道从开环极点出来以后根轨迹最初是向什么方向走的，就可以画得更加准确了。

广义根轨迹

之前画的根轨迹都是以K*从零到正无穷变化，而且有两个限制条件：开环传递函数为有理函数（这样才能找到开零点、极点）、系统为负反馈（正反馈有一个符号变化，不适用之前的公式）。但当需要分析其他参数或者不满足这两个限制条件的情况，画的根轨迹称为广义根轨迹。

参数根轨迹

以非K*的参数变化时系统的根轨迹

这类根轨迹绘制的时候规则和之前的根轨迹相同，但是需要先求出系统的等效开环传递函数

所谓的等效开环传递函数，就是当求出特征方程之后，把待求的参数变换成开环增益的形式，重新构建一个开环传递函数

这里有一个规律，对于单位反馈函数，特征方程LHS=开环传递函数分子+分母，所以构建等效开环传递函数的时候可以自由搭配什么在分子什么在分母

零度根轨迹

也就是系统实际处于正反馈的时候的根轨迹
由于是正反馈，所以传递函数：
$\Phi =\frac{G(s)}{1-G(s)H(s)}$
与负反馈相比从1+变成了1-，所以对应的法则也会改变：

1. 相角条件
   从$(2k+1)\pi$变成了$2k\pi$
   
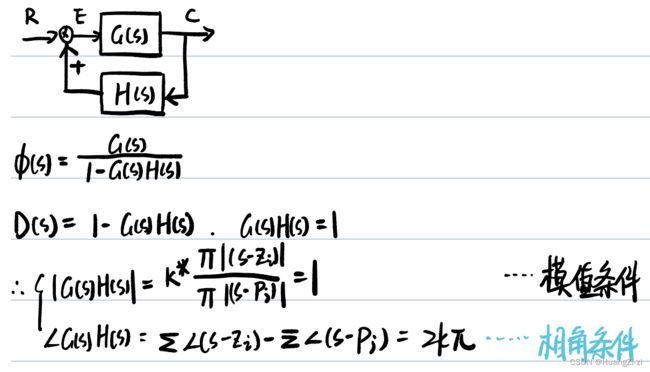
   由于相角条件变为$2K\pi$，对应0度的位置，因此被称为零度根轨迹。对应的，负反馈系统的根轨迹，相角条件为$(2K+1)\pi$，对应180度位置，因此被称为180度根轨迹。

2. 实轴上的根轨迹
   从实轴上最右端的开环零点或极点算起（从1算起），偶数开环零极点到奇数开环零极点之间的区域是根轨迹
   另外一种表述：某一区域右边开环零极点个数之和为偶数，则这一个区域为根轨迹
   注意：0也是偶数

3. 渐近线
   $\{\begin{array}{rl}{\sigma }_a& =\frac{\sum _{i=1}^n{p}_i-\sum _{j=1}^n{z}_j}{n-m}\\ & \\ {\phi }_a& =\frac{2k\pi }{n-m}\end{array}$
   渐近线与实轴的交角改为2kπ/n-m

4. 出射角/入射角
   相角条件改变因此这里也改变：
   $\sum _{j=1}^m\angle (s-z_j)-\sum _{i=1}^n\angle (s-p_i)=2k\pi$

其他法则和之前是一样的。

稍微补充一下：

零度根轨迹和一百八十度根轨迹往往呈现一种“互补”