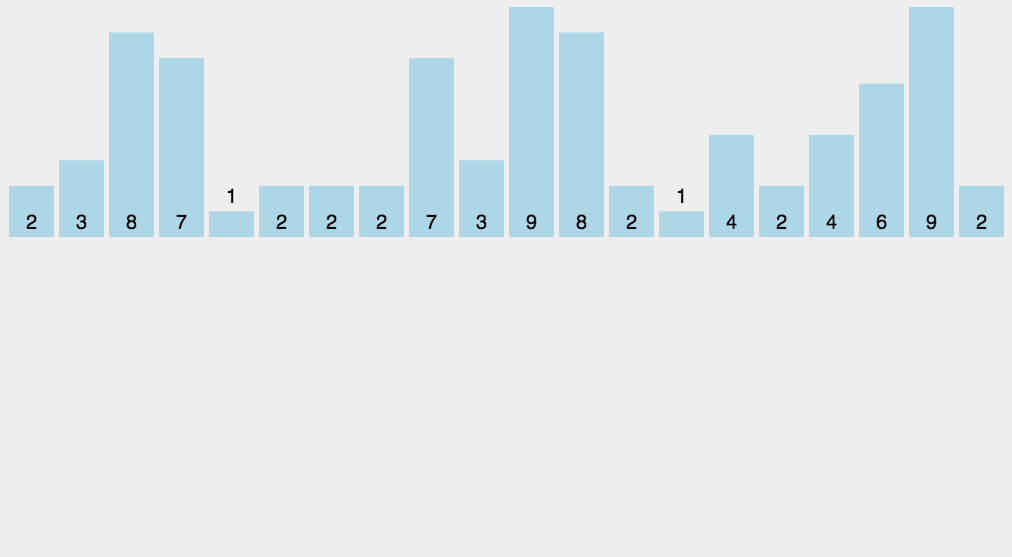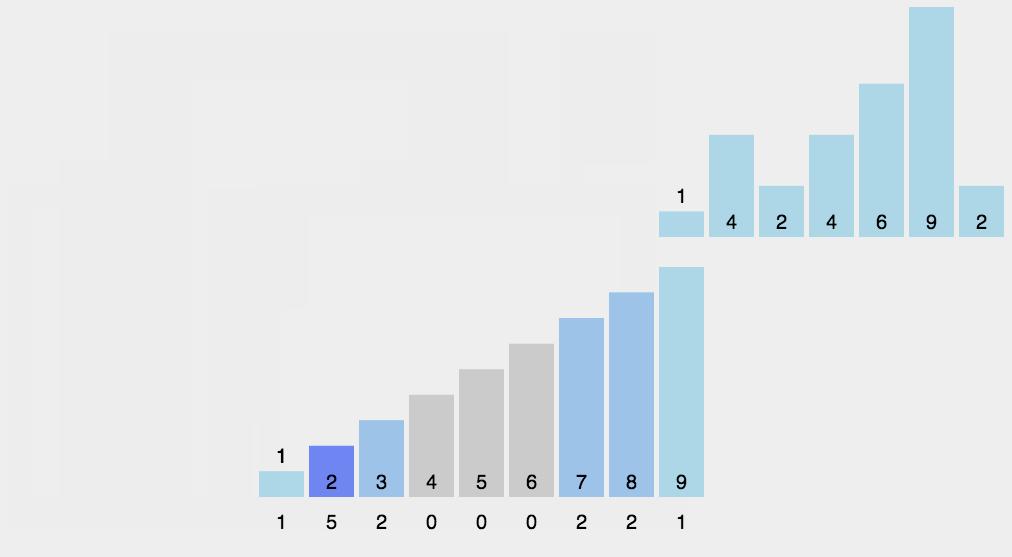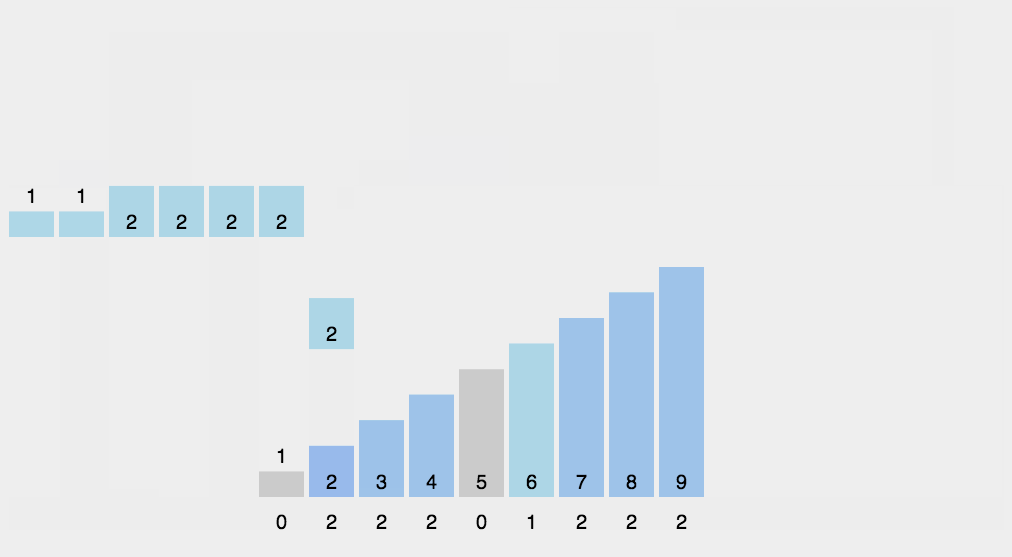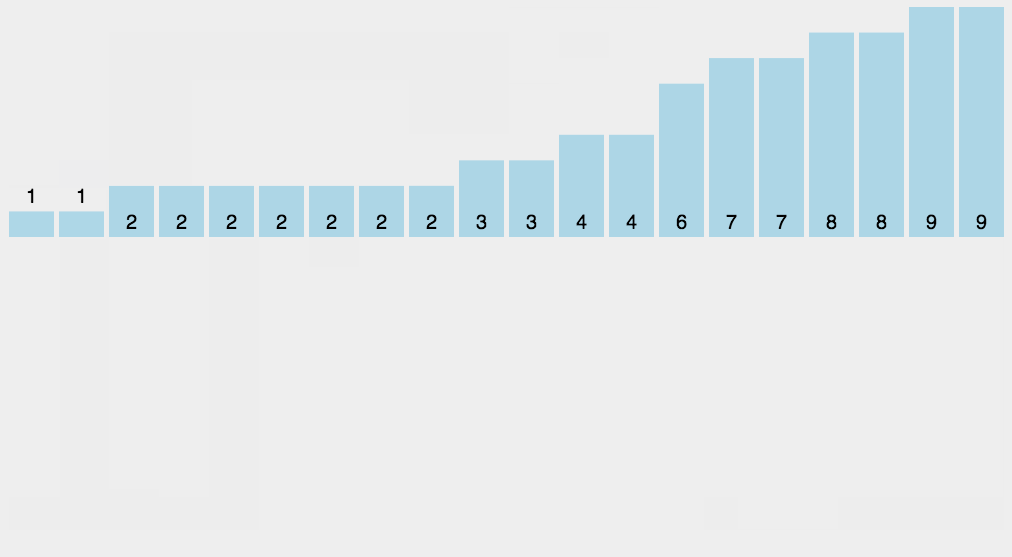算法系列十一：十大经典排序算法之——计数排序

1. 计数排序

• 什么是计数排序？
  计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。 当然这是一种牺牲空间换取时间的做法，而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序，堆排序）

• 时间复杂度 O(n + k)

• 空间复杂度 O(n + k)

• 稳定性：稳定。

1.1 算法思想

计数排序对输入的数据有附加的限制条件：
1、输入的线性表的元素属于有限偏序集S；
2、设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。
在这两个条件下，计数排序的复杂性为O(n)。
计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

1.2 排序过程

1. 根据待排序集合中最大元素和最小元素的差值范围，申请额外空间（max - min + 1）；
2. 遍历待排序集合，将每一个元素出现的次数记录到元素值对应的额外空间内；
3. 对额外空间内数据进行计算，得出每一个元素的正确位置；
4. 将待排序集合每一个元素移动到计算得出的正确位置上。

1.3 算法详解

（援引自他人）
假设 20 个数列为：{9, 3, 5, 4, 9, 1, 2, 7, 8，1，3, 6, 5, 3, 4, 0, 10, 9, 7, 9}。

根据排序过程，先遍历这个无序的随机数组，找出最大值为 10 和最小值为 0。那么我们对应的计数范围将是 0 ~ 10。然后每一个整数按照其值对号入座，对应数组下标的元素进行加1操作。

比如第一个整数是 9，那么数组下标为 9 的元素加 1，如下图所示。

第二个整数是3，那么对应数组下标为3的元素加1，如下图：

按照这样的规律继续遍历数组并填充直到最后。数组变成如下：

注意，这里每个下标位置都与元素相同，且存放的是该元素出现的次数。接下来，进行排序，依次遍历数组，输出下标值，每个下标里存放的是几就输出几个该下标值。最后输出的结果就是已排好序的数列。

0, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 9, 10

有没有感受到这个算法其实对待排序序列有很多限制。下面总结。

1.4 动图演示

1.5 代码实例

public static int[] countSort(int[] array) {
        //1.得到数列的最大值与最小值，并算出差值d
        int max = array[0];
        int min = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
            if(array[i] < min) {
                min = array[i];
            }
        }
        int d = max - min;
        //2.创建基于差值长度的统计数组并统计填充对应元素个数
        int[] countArray = new int[d + 1];
        for (int i = 0; i < array.length; i++) {
            countArray[array[i] - min]++;
        }
        //3.统计数组变形，后面的元素等于前面的元素之和
        for (int i = 0; i < countArray.length; i++) {
            countArray[i] = countArray[i] + countArray[i-1];
        }
        //4.倒序遍历原始数组，从统计数组找到正确位置，输出到结果数组
        int[] sortedArray = new int[array.length];
        for (int i = array.length - 1; i >=0 0; --i) {
        	int index = countArray[array[i] - min] -1;
            sortedArray[index] = array[i];//按存取的方式取出临时数组的元素
            countArray[array[i] - min]--;  // 临时数组相应位置减1
        }
        return sortedArray;
    }

解释

针对代码里：
第一步，很简单求最大最小值，不讲；
第二步：

• 为什么要基于差值创建统计数组？
  比如序列范围是90 ~ 99 ，如果按照最大值创建，那就需要长度100的数组，空间极大的浪费；
  如果按照差值，创建长度为9的数组，就会好很多。
• 理解 countArray[array[i] - min]++; 语句

基于差值，每个元素在统计数组的位置也是减去最小值之后的下标位置。

第三步：为什么要变形？为什么要后面的元素等于前面元素之和？
是为了让元素的相对位置排序后不发生交换。（前缀和）

第四步：为什么要倒序遍历原始数组？
和第三步配合使得排序稳定。（从前往后遍历，相同元素的话，前面的元素则会先归位再减一，这样则会使计数排序变成不稳定的排序算法）

2. 总结

• 如果原始数列的规模是N，最大最小整数的差值是M，由于代码中第1、2、4步都涉及到遍历原始数列，运算量都是N，第3步遍历统计数列，运算量是M，所以总体运算量是3N+M，去掉系数，时间复杂度是O(N+M)。

• 至于空间复杂度，如果不考虑结果数组，只考虑统计数组的话，空间复杂度是O(M)。

• 虽然计数排序看上去很强大，但是它存在两大局限性：

1.当数列最大最小值差距过大时，并不适用于计数排序
比如给定20个随机整数，范围在0到1亿之间，此时如果使用计数排序的话，就需要创建长度为1亿的数组，不但严重浪费了空间，而且时间复杂度也随之升高。

2.当数列元素不是整数时，并不适用于计数排序
如果数列中的元素都是小数，比如3.1415，或是0.00000001这样子，则无法创建对应的统计数组，这样显然无法进行计数排序。

正是由于这两大局限性，才使得计数排序不像快速排序、归并排序那样被人们广泛适用。