深度学习---从入门到放弃（四）优化器

深度学习—从入门到放弃（四）优化器

1.案例引入-MNIST手写数字识别

现代深度学习优化中的许多核心思想（和技巧）可以在训练 MLP 以解决图像分类任务的中进行说明。

在这里我们使用的是手写数字的 MNIST 数据集，上图为MNIST数据集的部分展示。

1.1 网络构建思路

1.网络种类：MLP
通常来说在对于图片的分类上，卷积神经网络（CNN）应用更为广泛且效果更好，但是鉴于目前只了解了MLP，那么请允许我用MLP来进行引入！
在这里我们选择一个只有一个隐藏层的MLP。
2.数据输入
我们拿到的原始数据是图片，而神经网络的输入一般为vector（也就是矢量），所以在这里我们放大每一张图片，将其中的每一像素块的位置及亮度用一个大的矩阵来表示，如下图：

3.结果输出
对于MLP分类任务而言，输出的是十个分类标签，因此我们需要将输出结果转换为输入数字分别为十个分类标签的概率。这里我们就要用到softmax函数，这样最终的输出就为总和为1的概率分布。
关于softmax

1.2 数据准备

def load_mnist_data(change_tensors=False, download=False):
  """Load training and test examples for the MNIST digits dataset

  Returns:
    train_data (tensor): training input tensor of size (train_size x 784)
    train_target (tensor): training 0-9 integer label tensor of size (train_size)
    test_data (tensor): test input tensor of size (70k-train_size x 784)
    test_target (tensor): training 0-9 integer label tensor of size (70k-train_size)

  """
  # Load train and test sets
  train_set = datasets.MNIST(root='.', train=True, download=download,
                             transform=torchvision.transforms.ToTensor())
  test_set = datasets.MNIST(root='.', train=False, download=download,
                            transform=torchvision.transforms.ToTensor())

  # Original data is in range [0, 255]. We normalize the data wrt its mean and std_dev.
  ## Note that we only used *training set* information to compute mean and std
  mean = train_set.data.float().mean()
  std = train_set.data.float().std()

  if change_tensors:
    # Apply normalization directly to the tensors containing the dataset
    train_set.data = (train_set.data.float() - mean) / std
    test_set.data = (test_set.data.float() - mean) / std
  else:
    tform = torchvision.transforms.Compose([torchvision.transforms.ToTensor(),
                                            torchvision.transforms.Normalize(mean=[mean / 255.], std=[std / 255.])
                                            ])
    train_set = datasets.MNIST(root='.', train=True, download=download,
                               transform=tform)
    test_set = datasets.MNIST(root='.', train=False, download=download,
                              transform=tform)

  return train_set, test_set


train_set, test_set = load_mnist_data(change_tensors=True)

1.3 建立网络

class MLP(nn.Module):

  def __init__(self, in_dim=784, out_dim=10, hidden_dims=[], use_bias=True):
    """建立MLP

    Args:
        in_dim (int): 输入数据的维度28*28=784
        out_dim (int): 类的数量10
        hidden_dims (list): 线性模型构成了一种非常特殊的 MLP：它们等效于具有零隐藏层的 MLP 
    """

    super(MLP, self).__init__()

    self.in_dim = in_dim
    self.out_dim = out_dim
 
    if len(hidden_dims) == 0:
      layers = [nn.Linear(in_dim, out_dim, bias=use_bias)]#在这里我们建立的是零隐藏层的 MLP 
    else:
      layers = [nn.Linear(in_dim, hidden_dims[0], bias=use_bias), nn.ReLU()]
      for i, hidden_dim in enumerate(hidden_dims[:-1]):
        layers += [nn.Linear(hidden_dim, hidden_dims[i + 1], bias=use_bias),
                   nn.ReLU()]

      # Add final layer to the number of classes
      layers += [nn.Linear(hidden_dims[-1], out_dim, bias=use_bias)]

    self.main = nn.Sequential(*layers)

  def forward(self, x):
    # 图片转 vector
    transformed_x = x.view(-1, self.in_dim)
    hidden_output = self.main(transformed_x)
    output = F.log_softmax(hidden_output, dim=1)#softmax输出概率分布
    return output

MLP(
(main): Sequential(
(0): Linear(in_features=784, out_features=10, bias=True)
)
)

在结束对神经网络的结构设计之后，我们就需要开始编写训练神经网络的代码，而优化器的选择就变成了一个至关重要的问题。

我们现在有一个带有相应可训练参数的模型以及一个要优化的目标函数（在这里我们采用分类任务中常用的交叉熵损失作为目标函数）。我们下一步要去哪里？我们如何找到“好的”参数配置？

2.梯度下降

相信大家对于梯度下降都不陌生，在简单线性神经网络里我们详细的说到了梯度下降的具体操作步骤，但是今天我们换一个思路，梯度下降在哪些情况里是最优选择呢？

要想回答这个问题，我们先引入这么一个场景：

如果你想到达这个二次函数的最低点，那么你可以一直向前走，或者一直后退，直到到达谷底。这是一个非常简单的过程，因为自始至终你只用选择前进或者后退这两个方向；

那么再考虑一下现实世界中用于深度学习训练的数据，它们之中很多都是高维数据，换句话说，优化目标函数时可选的方向变得非常多，而这个时候单纯朝着一个方向走就行不通了，我们需要考虑每个方向对于优化当前目标函数的影响，虽然这样费时费力，但是总归是可以按部就班完成优化的目的。

以上情景也被称作random search，即随机搜索过程，而梯度下降里层层迭代最小化损失函数的方法就与我们在高维数据中考虑每个方向对于优化当前目标函数的影响的方法不谋而合！

• 总结：梯度下降可以用于处理高维数据，但是相应也会升高计算成本
• 一句话形容梯度下降：一直向前走，但是每一步都小心翼翼
  

3.momentum梯度动量下降

同样的我们先来引入一个场景：

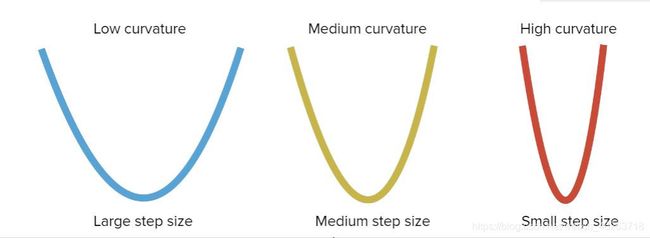
想象我们要到达上面这三个二次函数的最低点，对于开口较大的二次函数来说，坡度会比较缓，也就是说我们可以以较大的步长走向最低点；而对于开口较小，即坡度较陡的二次函数来说则是正好相反，我们必须以一个较小的步长前进，不然很可能一步跨过最低点。这里的步长指梯度下降中的学习率这一超参数。

基于以上情景，我们再回到现实世界的数据中去，如果在梯度下降的过程中既有需要较小步长，又有需要较大步长的时候该怎么办呢？我们可以将整个梯度下降过程想象为一个等高线图，我们从一个崎岖不平的山的山顶出发，刚开始十分陡峭，但是山势在山腰往下逐渐平缓，因此此时就需要我们走一步看一步，根据上一步的走法来调整下一步。

可以看到上一节说到的梯度下降在这种情况下表现得并不好。

而momentum方法可以确保在平缓的地方增大步长梯度下降，在陡峭的地方减小步长梯度下降。而之所以能达到这种效果是因为momentum在梯度下降里添加了一个$\beta (w_t-w_t{-}_1)$，将当前梯度下降与上一步梯度下降联系起来，利用上一次的结果不断进行修正，循环往复。

• 总结：momentum可以用来处理poor conditioning
• 一句话形容momentum：每走一步都要回头看看

4.non-convexity非凸性

之前我们所讨论的所有的例子都是只存在一个全局最小值的情况，这种情况在数学上叫做凸函数，如果我们要进行梯度下降的对象除了一个全局最小值还有很多个局部最小值，那那么此时该如何优化损失函数呢？

我们先来看一个非凸的例子：

我们可以清楚的发现这是一个十分凹凸不平的目标函数，如果我们按照以上所知任何一种梯度下降的方式进行优化，都有可能最终无法到达全局最小值，即下降会在触碰局部最小值时停止。这种情况也被叫做loss-landscape。

那么如何解决呢？既然我们的目标是到达全局最小值，而局部最小值会让梯度下降提前终止，那么我们只需要避开所有踩到局部最小值的路线就可以了！我们的路线的选择是跟初始化的起点有关的，所以解决非凸性梯度下降的关键点就是找到一个较好的起点。

既然非凸性和梯度下降的初始化紧密相关，那么我们只要将模型改造为对初始化不再敏感问题不就解决了吗！

增加网络深度和宽度可以让网络对于初始化的敏感性降低，但是过度增加深度和宽度，也会导致过度参数化，过拟合的问题。

• 总结：非凸性可以通过增加网络深度和宽度来解决

5.mini-batches小批次梯度下降

计算成本较高的大型神经网络中常采用小批次梯度下降这一策略

6.超参数微调

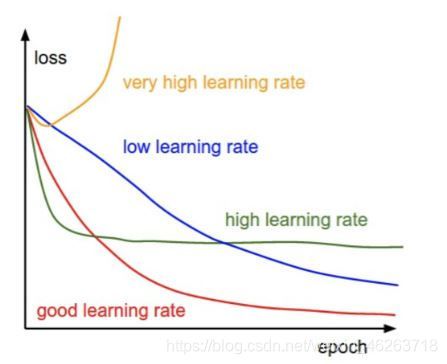
6.1 学习率

6.1 Adagrad

• 梯度下降过程中会对每一次下降参数的学习率进行调整
• 一般用在小批次梯度下降中

6.2 RMSprop

• 可用于目标函数存在非凸性的情况

7.总结

欢迎大家关注公众号奇趣多多一起交流！

深度学习—从入门到放弃(一)pytorch基础
深度学习—从入门到放弃（二）简单线性神经网络
深度学习—从入门到放弃（三)多层感知器MLP