c++ 字典顺序生成全排列，蛮力算法时间复杂度 Θ(n*n!)
什么是字典顺序:
1,3,4...n （不是）
1,3,2,4...n （不是）
1,2,3,4...n （是）
1. 我们先看下（按照字典顺序下一个最大排列是什么？）
{1,2,3} 字典顺序全排列 {1,2,3} {1,3,2} {2,1,3} {2,3,1} {3,1,2} {3,2,1}
例1：从上面随机选择一个排列 {2,1,3} 字典顺序下一个最大排列 {2,3,1}
例2：从上面随机选择一个排列 {3,1,2} 字典顺序下一个最大排列 {3,2,1}
例3：从上面随机选择一个排列 {3,2,1} 字典顺序下一个最大排列 {3,2,1}（是它自身, 没有比它更大的）
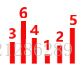
例4：那 362541 呢？是不是要先全排列出来，然后再去找？（答案是NO）——PS: 数字越大，
越高
解:① 从右到左寻找第一个 “ 信号由(无或弱)到强突然转弱 ” 的位置 
，也就是底下指向 2 的红色箭头所属的位置
② 取 
中大于 
的最小数，也就是指向 4 的红色箭头所属的位置，然后两个数交换位置 
③ 以从左到右递增的形式对 
进行排序 ，最终结果为 
visual Studio程序直接复制即可运行！
#include
#include
using namespace std; template // 字典顺序生成下一个最大排列 // Θ(n)
void nextPermutation(T list[], int n)
{
// 解:①
int j = n - 1;
while (list[j] > list[j + 1]) // n 次比较
{
if (j == 0)
{
copy(list, list + n + 1, ostream_iterator(cout, " "));// 打印自身
return; // 防止 j -= 1 "越位"
}
j -= 1;
}
// 解:②
int k = n;
while (list[j] > list[k]) // n-j 次比较，1<=j s) // (n-j)/2+1 次比较，1<=j(cout, " "));
cout << endl;
}
int main()
{
int arr[6] = { 3,6,2,5,4,1 };
nextPermutation(arr, 5);
system("pause");
return 0;
} 2. 刚刚是下一个, 那( 按照字典顺序上一个最大排列是什么？）
{1,2,3} 字典顺序全排列 {1,2,3} {1,3,2} {2,1,3} {2,3,1} {3,1,2} {3,2,1}
例1：从上面随机选择一个排列 {2,1,3} 字典顺序上一个最大排列 {1,3,2}
例2：从上面随机选择一个排列 {3,1,2} 字典顺序上一个最大排列 {2,3,1}
和上面介绍的原理相同，只要把上面的操作反过来，小小的修改即可，这里不在过多介绍，直接上代码
visual Studio程序直接复制即可运行！
#include
#include
using namespace std; template // 字典顺序生成上一个最大排列 // Θ(n)
void previousPermutation(T list[], int n)
{
int j = n - 1;
while (list[j] < list[j + 1])
{
if (j == 0)
{
copy(list, list + n + 1, ostream_iterator(cout, " "));
return;
}
j -= 1;
}
int k = n;
while (list[j] < list[k])
k -= 1;
swap(list[j], list[k]);
int r = n, s = j + 1;
while (r > s)
{
swap(list[r], list[s]);
r -= 1;
s += 1;
}
copy(list, list + n + 1, ostream_iterator(cout, " "));
cout << endl;
}
int main()
{
int arr[6] = { 3,6,4,1,2,5 };
previousPermutation(arr, 5);
system("pause");
return 0;
} 3. 终于进入全排列了
例1：我们已经可以实现 集合的下一个最大排列，比如 {1,2,3} 字典顺序下一个最大排列 {1,3,2}，可是就只输出一个
{1,2,3} 字典顺序全排列 {1,2,3} {1,3,2} {2,1,3} {2,3,1} {3,1,2} {3,2,1}
解：① 只要让 nextPermutation 不断的循环下去, 就可以不断的寻找下一个最大排列，其中必须给循环一个停止条件
② {1,2,3}全排列停止条件{3,2,1} , 因为 {3,2,1} 字典顺序下一个最大排列 {3,2,1}（是它自身, 没有比它更大的）
③.1 期间遍历每个排列中的从右到左相邻两元素 
如果满足从右到左寻找第一个 “ 信号由(无或弱)到强突然转弱 ” 的位置 
也就是指向 2 的红色箭头所属的位置
循环继续，一直运行到循环的停止条件
③.2 期间遍历每个排列中的从右到左相邻两元素
,不满足第一个 “ 信号由(无或弱)到强突然转弱 ” 继续
如果满足从右到左寻找第一个 “ 信号由(无或弱)到强突然转弱 ” 的位置 
也就是指向 1 的红色箭头所属的位置
循环继续，一直运行到循环的停止条件
④运行到 {3,2,1} 
和 
都不满足第一个 “ 信号由(无或弱)到强突然转弱 ” ，表示全排列结束，退出程序
visual Studio程序直接复制即可运行！
#include
#include
using namespace std; template // 字典顺序生成全排列 // Θ(n*n!)
void dictionaryPermutation(T list[], int n)
{
copy(list, list + n + 1, ostream_iterator(cout, " "));
cout << endl;
/*动态申请的内存空间要充足，不然会造成内存溢出*/
T* arr = new T[n + 1];
for (int i = 0; i <= n; i++)
arr[i] = list[i];
/*遍历每一个元素*/
for (int j = n - 1; j >= 0; j--)
{
/*遍历到最大排列的时候结束*/
while (list[j] < list[j + 1]) // n! 比较次数
{
nextPermutation(list, n); // n!*Θ(n) 比较次数
j = n - 1;
}
}
delete[] arr;
}
int main()
{
int arr[3] = { 1,2,3 };
dictionaryPermutation(arr, 2);
system("pause");
return 0;
} 例2：我们已经可以实现 集合的上一个最大排列，比如 {3,2,1} 字典顺序上一个最大排列 {3,1,2}，可是就只输出一个
{3,2,1} 字典顺序全排列 {3,2,1} {3,1,2} {2,3,1} {2,1,3} {1,3,2} {1,2,3}
解：① 只要把 nextPermutation 替换成 previousPermutation，再做小小的修改
visual Studio程序直接复制即可运行！
#include
#include
using namespace std; template // 字典顺序生成全排列 // Θ(n*n!)
void dictionaryPermutation(T list[], int n)
{
copy(list, list + n + 1, ostream_iterator(cout, " "));
cout << endl;
/*动态申请的内存空间要充足，不然会造成内存溢出*/
T* arr = new T[n + 1];
for (int i = 0; i <= n; i++)
arr[i] = list[i];
/*遍历每一个元素*/
for (int j = n - 1; j >= 0; j--)
{
/*遍历到最小排列的时候结束*/
while (arr[j] > arr[j + 1])
{
previousPermutation(arr, n);
j = n - 1;
}
}
delete[] arr;
}
int main()
{
int arr[3] = { 3,2,1 };
dictionaryPermutation(arr, 2);
system("pause");
return 0;
} {2,1,3} 字典顺序全排列 {2,1,3} {2,3,1} {3,1,2} {3,2,1} {1,3,2} {1,2,3}
输入: {2,1,3} nextPermutation {2,3,1} {3,1,2} {3,2,1}
{2,1,3} previousPermutation {1,2,3} {1,3,2}
说好的全排列呢？给我吃了？
别急，在 dictionaryPermutation 中把 nextPermutation 和 previousPermutation，做一个简单组合即可
visual Studio程序直接复制即可运行！
#include
#include
using namespace std; template // 字典顺序生成全排列 // Θ(n*n!)
void dictionaryPermutation(T list[], int n)
{
copy(list, list + n + 1, ostream_iterator(cout, " "));
cout << endl;
/*动态申请的内存空间要充足，不然会造成内存溢出*/
T* arr = new T[n + 1];
for (int i = 0; i <= n; i++)
arr[i] = list[i];
/*遍历每一个元素*/
for (int j = n - 1; j >= 0; j--)
{
/*遍历到最大排列的时候结束*/
while (list[j] < list[j + 1]) // n! 比较次数
{
nextPermutation(list, n); // n!*Θ(n) 比较次数
j = n - 1;
}
/*遍历到最小排列的时候结束*/
while (arr[j] > arr[j + 1])
{
previousPermutation(arr, n);
j = n - 1;
}
}
delete[] arr;
}
int main()
{
int arr[3] = { 2,1,3 };
dictionaryPermutation(arr, 2);
system("pause");
return 0;
} 到此结束
各位如有对此文章讲解的内容有任何想法和建议的欢迎留言