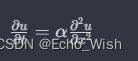Scipy 高级教程——解决偏微分方程
Python Scipy 高级教程:解决偏微分方程
Scipy 提供了强大的数值求解工具,其中包括解决偏微分方程(PDEs)的功能。在本篇博客中,我们将深入介绍 Scipy 中解决偏微分方程的方法,并通过实例演示如何应用这些工具。
1. 一维热传导方程
我们将从一维热传导方程的数值求解开始。考虑以下的一维热传导方程:
其中 u 是温度分布, t 是时间, x 是空间。我们使用 Scipy 的 solve_ivp 函数进行数值求解。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# 定义热传导方程
def heat_equation(t, u, alpha, dx):
du_dx2 = np.gradient(np.gradient(u, dx), dx)
return alpha * du_dx2
# 定义初始条件和空间网格
initial_condition = np.sin(np.pi * np.linspace(0, 1, 100))
space_grid = np.linspace(0, 1, 100)
# 求解热传导方程
solution = solve_ivp(heat_equation, [0, 0.1], initial_condition, args=(0.01, space_grid), t_eval=[0, 0.02, 0.05, 0.1])
# 绘制温度分布随时间的演化
plt.figure(figsize=(10, 6))
for i in range(len(solution.t)):
plt.plot(space_grid, solution.y[:, i], label=f't={solution.t[i]:.2f}')
plt.xlabel('空间')
plt.ylabel('温度分布')
plt.title('一维热传导方程的数值求解')
plt.legend()
plt.show()
在这个例子中,我们定义了一维热传导方程的求解函数,并使用 solve_ivp 进行数值求解。最后,绘制了温度分布随时间的演化。
- 二维波动方程
接下来,我们考虑二维波动方程的数值求解。波动方程表示为:
其中 u 是振幅, t 是时间,x 和 y 是空间。我们使用 solve_ivp 进行数值求解。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.integrate import solve_ivp
# 定义二维波动方程
def wave_equation(t, u, c, dx, dy):
du_dx2 = np.gradient(np.gradient(u, dx, axis=0), dx, axis=0)
du_dy2 = np.gradient(np.gradient(u, dy, axis=1), dy, axis=1)
return c**2 * (du_dx2 + du_dy2)
# 定义初始条件和空间网格
initial_condition = np.exp(-((np.linspace(0, 1, 50) - 0.5)**2 + (np.linspace(0, 1, 50) - 0.5)**2) / 0.1)
space_grid_x, space_grid_y = np.meshgrid(np.linspace(0, 1, 50), np.linspace(0, 1, 50))
# 求解二维波动方程
solution = solve_ivp(wave_equation, [0, 1], initial_condition.flatten(), args=(1.0, space_grid_x, space_grid_y),
t_eval=np.linspace(0, 1, 50))
# 绘制振幅随时间的演化
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
for i in range(len(solution.t)):
ax.plot_surface(space_grid_x, space_grid_y, solution.y[:, i].reshape((50, 50)), cmap='viridis', alpha=0.5,
rstride=100, cstride=100)
ax.set_xlabel('空间 X')
ax.set_ylabel('空间 Y')
ax.set_zlabel('振幅')
ax.set_title('二维波动方程的数值求解')
plt.show()
在这个例子中,我们定义了二维波动方程的求解函数,并使用 solve_ivp 进行数值求解。最后,绘制了振幅随时间的演化的三维图。
3. 总结
通过本篇博客的介绍,你可以更好地理解和使用 Scipy 中解决偏微分方程的方法。这些方法对于模拟物理现象、仿真动力学系统等有广泛的应用。在实际应用中,根据具体问题选择合适的数值求解方法和工具将有助于提高模拟的准确性和可靠性。希望这篇博客对你有所帮助!