卷积——相关知识点总结

一、2D卷积（2D Convolution）

1.公式

  卷积运算（Convolution）定义：一种通过两个函数和生成第三个函数的一种数学算子，公式如下。通常将函数$f$称为输入（input），函数$g$称为卷积核（kernel），函数$h$称为特征图谱（feature map）。
$$h(t)={\int }_{}g(t-t^{\prime })f(t)\mathrm{d}{t}^{\prime }$$
  离散多维卷积（深度学习领域最常见的情况），即输入是一个多维数组，卷积核也是一个多维数组，时间上是离散的，因此无限的积分变成有限的数组有限元素的加和：
$$H(i,j)=\sum _m\sum _{n}F(m,n)G(i-m,j-n)$$
  上式表明先对卷积核翻转，再与输入点乘、求和得到输出。而在卷积的实现中通常省去了翻转，即其实为互相关(Cross-Correlation)。公式如下:
$$H(i,j)=\sum _m\sum _{n}F(m,n)G(i+m,j+n)$$

注：1).数学中的卷积，根据使用场景（例：信号强度随时间衰弱），故
   需‘’卷积核‘’翻转180度。
  2).神经网络中的‘’卷积‘’，为了提取图像特征，只借鉴了加权求和
   的特点。 其卷积核由于是不断学习更新的，故不需翻转。
 且数学中的‘’卷积核‘’是给定的，而神经网络中可学习的未知参数。
 

2.核心思想

可参考花书P203-P207

(1).稀疏交互。局部连接（feature map局部与卷积核互相关），相对全连接网络参数大大减少。在二维图像中，局部像素的关联性强，CNN突出了对图像局部特征的强响应能力。
(2).参数共享。（卷积核的滑动）一个feature map共享一个卷积核的参数权重，相对全连接减少了整体参数量，增强了网络训练效率。
(3).等变表示。（参数共享–>平移等变）例：对图像进行右移后卷积，与先卷积后右移，得到的结果一样。即特征对位置不敏感，对分类有益，但对与位置相关的任务（如目标检测、语义分割）不利。
 
特点：下采样，降低图片分辨率，数据降维，使浅层的局部特征组合为深层特征。相对全连接，减少计算资源消耗，加速模型训练，有效控制过拟合。
 

3.计算公式

(1).特征图尺寸：

     ——1D\2D\3D卷积相同
$$output=\lfloor \frac{input-kernel+2\ast padding}{stride}\rfloor +1$$

(2).参数量（parameters）
$$params=C_o\times (k_w\times k_h\times C_i+1)$$
  其中，$C_o$表示输出通道数，$C_i$表示输入通道数，$k_w\times k_h\times C_i$表示一个卷积核的权重数量，1为bias参数量。故常规方形卷积核公式为：
$$params=C_o\times (k^2\times C_i+1)$$
  另，全连接的参数量公式：
$$params=(I+1)\times O$$

(3).FLOPs (floating point of operations)，浮点运算次数。即计算量，衡量算法/模型复杂度。
$$FLOPs=[(C_i\times k_w\times k_h)+(C_i\times k_w\times k_h-1)+1]\times C_o\times W\times H$$
  其中，$(C_i\times k_w\times k_h)$表示一次卷积操作中的乘法运算量，$(C_i\times k_w\times k_h-1)$表示一次卷积操作中的加法运算量，1表示bias的加法计算量，$C_o\times W\times H$表示feature map的所有元素数。故常规方形卷积核公式为：
$$FLOPs=C_i\times k^2\times C_o\times W\times H$$
 注：区分，FLOPS (floating point of per second)，每秒浮点运算次数。即计算速度，衡量硬件的性能。

  另，全连接的FLOPs公式：
$$FLOPs=[I+(I-1)+1\times O]=2\times I\times O$$
  其中，$I$为input neurons，$O$为output neurons，中括号中$I$表示乘法运算量，$I-1$表示加法运算量，1表示bias加法运算量，$\times O$表示计算O个神经元的值。

 

4. 代码

(1).torch调用（省略常见基础参数）

 参考torch官方文档

import torch.nn as nn

nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, 
		  dilation=1, groups=1, bias=True, padding_mode='zeros')

参数	描述
padding_mode (str, optional)	默认为'zeros'，填充0； 'reflect'以矩阵边缘为对称轴，将矩阵中的元素对称地填充到最外围； 'replicate'将矩阵的边缘复制并填充到矩阵的外围； 'circular'矩阵循环，以原矩阵为中心截取所需size矩阵。 参考样例
dilation (int or tuple, optional)	卷积核内元素间的间隔，默认为1。大于1时，即为空洞卷积。
groups (int, optional)	分组卷积，默认为1。

 注：conv = nn.unfold + torch.matmul + nn.fold

(2).基于python 与 numpy 的实现

import numpy as np


def zero_pad(x, pad_height, pad_width):
    H, W = x.shape
    out = np.zeros((H+2*pad_height, W+2*pad_width))
    out[pad_height:pad_height+H, pad_width:pad_width+W] = x     # 在tensor中填入x
    return out


def conv_fast(input, kernel):
    H, W = input.shape
    h, w = kernel.shape
    out = np.zeros((H, W))

    # 自适应padding，input.size() == output.size()
    pad_height = h // 2
    pad_width = w // 2
    input_padding = zero_pad(input, pad_height, pad_width)

    for i in range(H):
        for j in range(W):
            out[i][j] = np.sum(np.multiply(kernel, input_padding[i:(i+h), j:(j+w)]))    # 加权求和后填入out的对应位置，stride=1

    return out


input = np.array([[1, 2, 3, 4],
                  [5, 6, 7, 8],
                  [9, 10, 11, 12],
                  [13, 14, 15, 16]])
kernel = np.array([[-1, -2, -1],
                   [0, 0, 0],
                   [1, 2, 1]])

print('output:')
print(conv_fast(input, kernel))

 

5.延伸知识

(1).提取特征类型:
 浅层卷积–>边缘特征；中层卷积–>局部特征；深层卷积–>全局特征

(2).大小卷积核：
  常用的3x3卷积核，其两个叠加与5x5卷积核感受野大小一致，但参数量仅为5x5的10/13。且多进行的卷积操作，增加了模型的非线性表达能力。
  大卷积核（如7x7、9x9），在GAN、图像超分辨率、图像融合领域有较多应用。

(3).1x1卷积作用：
   1).使特征信息交互、整合；
   2).对特征图升维、降维(减少参数量)；
   3).增加非线性，提升网络表达能力。

(4).卷积核个数：输入通道数x输出通道数；bias个数：输出通道数。(参考验证)

(5).感受野Receptive field (RF)：在CNN中，为一层输出的特征图中每个元素在原始图像上映射的区域大小。
 计算公式：$R{F}_i=stride\times (R{F}_{i+1}-1)+kernel$    （更多参考）

(x).全连接层：
 1).将高维特征映射到label空间，可作为网络的分类器模块，可用于迁移学习；
 2).可使用全局平均池化(GAP)替代全连接层，既保持性能又减少参数。

 

二、其他卷积

1.1D卷积（1D Convolution）

 一维卷积常用于序列模型，自然语言处理领域。

 

• 代码（参数同2D卷积）

• import torch.nn as nn
  
  nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, 
  		  dilation=1, groups=1, bias=True, padding_mode='zeros')
  

  	size of feature map	size of kernel
  Conv1d	$(N,C,L)$	$(L_k)$
  Conv2d	$(N,C,H,W)$	$(H_k,W_k)$

  2.3D卷积（3D Convolution）

   三维卷积被普遍用在视频分类、动作识别、三维医学图像分割等任务。
  
    单通道的3D卷积过程，如上图所示。其与多通道2D卷积的区别在于在第三个维度（例如时间维度）卷积核的维度大小不是必须与输入该维度相等。卷积核在此方向上也进行滑动操作，故输出特征图也为3维。

  
    上图为多通道3D卷积，与单通道2D卷积–>多通道2D卷积同理。

   

• 代码（参数同2D卷积）

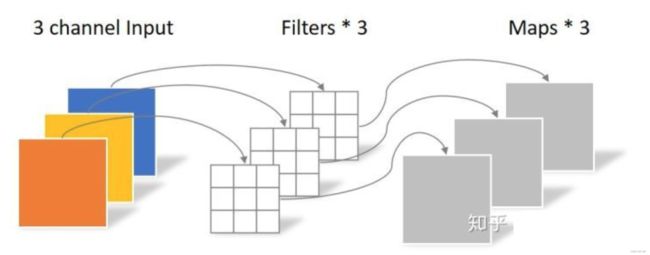
• import torch.nn as nn
  
  nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, 
  		  dilation=1, groups=1, bias=True, padding_mode='zeros')
  

  	size of feature map	size of kernel
  Conv2d	$(N,C,H,W)$	$(H_k,W_k)$
  Conv3d	$(N,C,D,H,W)$	$(D_k,H_k,W_k)$

  3.分组卷积（Grouped Convolution）

   groups参数为in_channels与out_channels的公约数。
  
    忽略bias，分组卷积参数量、计算量公式如下：
  $$params=g\times (\frac{C_o}{g}\times k^2\times \frac{C_i}{g})=\frac{1}{g}param{s}_{conv2d}$$
  $$FLOPs=g\times (\frac{C_i}{g}\times k^2\times \frac{C_o}{g}\times W\times H)=\frac{1}{g}FLOP{s}_{conv2d}$$

  4.空洞卷积（Dilated Convolution）

    空洞卷积最初的提出是为了解决图像分割的问题。常见的图像分割算法通常使用池化层和卷积层来增加感受野，同时也缩小了特征图尺寸，然后再利用上采样还原图像尺寸。特征图缩小再放大的过程造成了精度上的损失。而空洞卷积可以在增加感受野的同时保持特征图的尺寸不变（需padding），从而代替下采样和上采样操作。（引自文章）

  空洞卷积卷积核大小：$Kernel=kernel+（kernel-1）+（dilation-1）$

  (1).作用：
   1).扩大感受野：在deep net中，为能不丢失分辨率下扩大感受野，使用空洞卷积。这在检测，分割任务中十分有用：一方面感受野大了可以检测分割大目标；另一方面分辨率高了可以精确定位目标。
   2).捕获多尺度上下文信息：设置不同dilation时，获得不同感受野，即获取了多尺度信息。

  ps：1).在实际中不好优化，速度会大大折扣。
     2).语义分割由于需要获得较大的分辨率图，因此经常在网络的最后两个stage，取消下采样，采用空洞卷积弥补丢失的感受野。

  (2).gridding问题
   1).局部信息丢失：由于其类似于棋盘格式的计算方式，卷积信息缺少相关性。
   2).远距离获取的信息没有相关性：由于其稀疏的采样输入信号，使得远距离卷积得到的信息之间没有相关性，影响分类结果。

  更多参考：总结-空洞卷积(Dilated/Atrous Convolution)

  5.转置卷积/反卷积（Transposed Convolution）

    通过训练学习得到最优的上采样方式，替代传统的插值上采样，用于图像分割、图像融合、GAN等。

  注：其不是卷积的反向操作，卷积运算不可逆，仅恢复尺寸，并非数值。

   
  设卷积核尺寸$K\ast K$，输入特征图尺寸$F\ast F$。
  (1).stride = 1，padding = 0：
    先进行$padding=K-1$的填充，再进行卷积转置运算，输出特征图尺寸：$$output=F+(K-1)$$
  

  (2).stride > 1，padding = 0：
    先进行$padding=K-1$的填充，相邻元素间空洞大小为$stride-1$，再进行卷积转置运算，输出特征图尺寸：$$output=stride\times (F-1)+K$$
  
   

• 代码（参数同2D卷积）

• import torch.nn as nn
  
  nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, 
  				   output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')
  

  参数	描述
  output_padding	输出特征图的扩充尺寸

   1D\2D\3D转置卷积参数均相同，更多请参考官方文档

  6.深度可分离卷积（Depthwise Separable Convolution）

  • 逐通道卷积（Depthwise Convolution）

      即分组卷积（groups=in_channels）
  
            $params=k^2\times C_i$                  $FLOPs=C_i\times k^2\times W\times H$

  • 逐点卷积（Pointwise Convolution）

      即1x1卷积
  
   深度可分离卷积参数量公式：
  $$params=k^2\times C_i+C_i\times C_o$$
   深度可分离卷积计算量公式：
  $$FLOPs=C_i\times k^2\times W\times H+C_i\times C_o\times W\times H$$
   注：深度可分离卷积参数量是标准卷积的$\frac{1}{C_o}+\frac{1}{k^2}$

   

• 代码（参数同2D卷积）

• import torch.nn as nn
  
  class Depthwise_Separable_Conv(nn.Module):
      def __init__(self, ch_in, ch_out):
          super(Depthwise_Separable_Conv, self).__init__()
          self.depth_conv = torch.nn.Conv2d(ch_in, ch_in, kernel_size=3, groups=ch_in, bias=False)
          self.point_conv = torch.nn.Conv2d(ch_in, ch_out, kernel_size=1, bias=False)
  
      def forward(self, x):
          x = self.depth_conv(x)
          x = self.point_conv(x)
          return x
  

  7.空间可分卷积（Spatially Separable Convolution）& 平展卷积（Flattened convolutions）

   参考自[3]
   

• 空间可分卷积
• 
  
    即常规3x3卷积分解为：3x1卷积核先于图像卷积，再应用1x3卷积核。相对卷积运算的9个参数变为6个。卷积乘法运算由 $9\ast 9=81$降为 $(5\ast 3)\ast 3+(3\ast 3)\ast 3=72。$
  
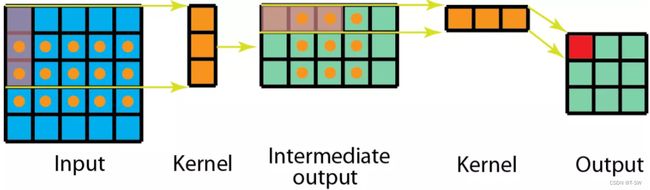
     缺点：元素减少，可能搜索的内核减少，导致模型性能较差。

   

• 平展卷积
• 
  
    如图所示，平展卷积将标准滤波器分解为3个1D滤波器，与空间可分卷积类似。 论文提到，随着分类问题难度的增加，将平展卷积直接应用于滤波器会导致显著的信息丢失。为了缓解此类问题，对感受野的连接进行限制，以便模型在训练时可以学习分解后的1D滤波器。通过使用由连续的 1D 过滤器组成的扁平化网络在 3D 空间的所有方向上训练模型，能够提供的性能与标准卷积网络相当，计算成本却更低很多。

  8.混洗分组卷积（Shuffled Grouped Convolution）

    由旷视在ShuffleNet首次提出。如下图所示，两次分组卷积中进行通道混洗。以此弥补分组卷积缺少的信息传递，增加不同分组的特征之间的信息流动, 提高性能。

  

  8.可变性卷积（Deformable Convolution）

    可变形卷积将标准卷积操作中采样位置增加了一个偏移量offset，这样卷积核就能在训练过程中扩展到很大的范围。推广了尺度、长宽比和旋转的各种变换。
  
  

   
   
   
  参考：
  1.卷积 Convolution 原理及可视化
  2.公众号：WeThinkIn
  3.详述Deep Learning中的各种卷积