论文阅读笔记AI篇 —— Transformer模型理论+实战 (二)

资源地址
Attention is all you need.pdf(0积分) - CSDN

第二遍阅读（通读）

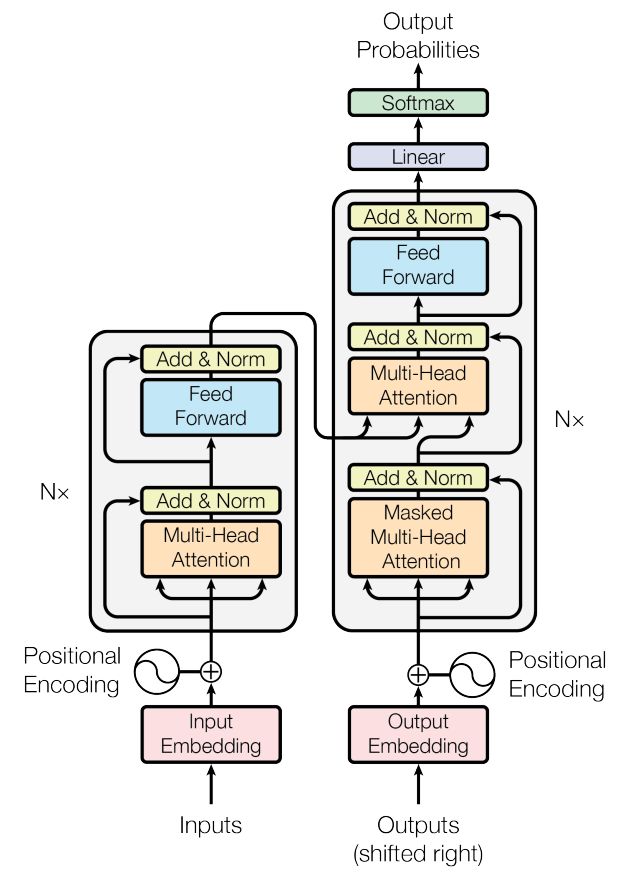
图1——Transformer结构图

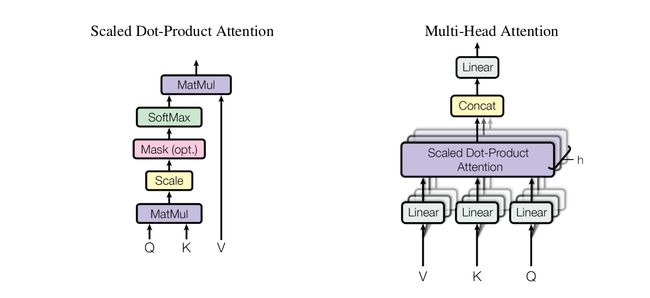
图2——Attention结构图

2.1 Background

Background中说，ByteNet和ConvS2S都使用了CNN结构作为基础模块去计算input和output之间的潜在联系，其中，关联来自两个任意输入或输出位置的信号所需的计算量，伴随着distance的增长而增长，ConvS2S呈线性增长，ByteNet呈对数增长，而在Transformer中，这个操作所需的计算量只是常数级别，尽管代价是平均了注意力的加权位置降低了有效分辨率（这里的有效分辨率是什么？），但作者用Multi-Head Attention机制去抵消了这个代价。（所以NLP的一个关键任务是，计算词语之间的相关度？）

Self-Attention 机制在 reading comprehension, abstractive summarization, textual entailment and learning task-independent sentence representations（阅读理解、抽象摘要、文本隐含和学习任务独立的句子表征）中都有成功的应用实践。

End-to-end memory networks are based on a recurrent attention mechanism instead of sequence aligned recurrence and have been shown to perform well on simple-language question answering and language modeling tasks.端到端记忆网络基于循环注意机制，而不是序列对齐递归，并已被证明在简单语言问题回答和语言建模任务上表现良好
那什么是End-to-end memory network？

看起来End-to-end memory networks和Transformer都一样，都是使用了attention mechanism，但是Transformer是更彻底一些，连recurrent、sequence-aligned（序列对齐）、convolution模块都没有，是entirely on self-attention，self-attention不是Transformer这篇论文首先提出的，但是就如同标题说的Attention is all you need，纯粹基于self-attention他们是第一个。后面的章节，作者就在讨论如何motivate self-attention和相比于(Convolutional sequence to sequence learning、Neural GPUs learn algorithms、Neural machine translation in linear time)这三篇论文的优势了。

2.1 参考文章或视频链接
[1] Textual Entailment（自然语言推理－文本蕴含） - AllenNLP
[2] 文本蕴涵(Textual entailment)

2.2 Model Architecture

Model Architecture在原文中是第三章节，这个章节里分了下面的小节。

• Encoder and Decoder Stacks
• Attention(两部分内容共同构建了Attention模块)
• • Scaled Dot-Product Attention
• • Multi-Head Attention
• • Applications of Attention in our Model
• Position-wise Feed-Forward Networks
• Embeddings and Softmax
• Positional Encoding (这个读第二遍不懂，读第三遍的时候重点解释)

在正式对Model Architecture行文前，作者说Transformer也遵循了Encoder先生成中间表示然后Decoder对中间表示进行decode的这么一个架构，并且是用stacked self-attention and point-wise, fully connected layers去实现的，这里有个point-wise, fully connected layers的网络，中文译名是逐点全连接层，其表达公式是
$$FFN(x)=max(0,x{W}_1+b_1)W_2+b_2$$
也就是说，两个Linear层中间夹着一个ReLU就是point-wise, fully connected layer，ReLU的表达式就是$max(0,x)$

图3 —— point-wise详细结构图（来自参考文章3）

也就对应于图1的这个Feed Forward的蓝色的这部分：

图4 —— point-wise全局结构图

2.2 参考文章或视频链接
[1] Position-Wise Feed-Forward Layer
[2] Position-wise Feed-Forward Network (FFN) - Github
[3] Illustrated Guide to Transformers- Step by Step Explanation
先看这篇 [4] The Annotated Transformer - Harvard NLP
[5] 《Transformer论文逐段精读【论文精读】》- 李沐
[6] 《Transformer详解（李沐大神文字版，干货满满！）》- CSDN

2.2.1 Encoder and Decoder Stacks

作者在这里分别描述了Encoder与Decoder。
Encoder是$N=6$层，每一层Encoder Layer有两个sub-layers，一个是multi-head self-attention，另一个是position-wise fully connected feed-forward network，然后都加上了残差连接与正则化Norm，也就是Add & Norm。
Decoder也是$N=6$层，除了Encoder已经有的两个sub-layers，还多了一部分Masked Multi-Head Attention，其作用是对encoder stack的输出进行multi-head attention的处理，看到下面这张图，不妨先忽略被蓝色方块掩盖住的Add & Norm，可以发现①和②两个部分高度一致，所以说Decoder也包括了Encoder的功能逻辑？这么说当然是没错的，我想，只要具备编码转换的这样一种逻辑coding A -> coding B，就是Encoder，至于叫Decoder，那是为了方便理解的人为命名。

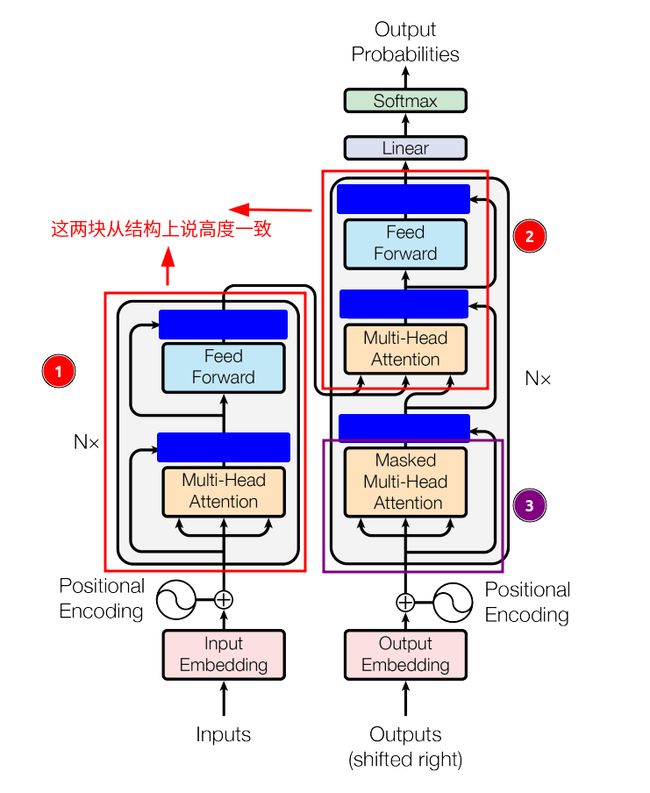
图5 —— Encoder-Decoder结构对比图

此外，应该对Add & Norm的作用感到有点好奇，Add就是将输出与残差连接相加，那Norm呢？Norm的作用是归一化，用来将消除梯度爆炸，比如权重已经训练到了一个瓶颈，即前后变化在指定范围内，那就该停止了，如果再训练那就容易导致overfitting过拟合，这就是正则化项的一个作用^[4]。

Q:BatchNorm与LayerNorm的区别？
请看李沐老师的讲解与参考文章[1]

2.2.1 参考文章或视频链接
[1] 《论文笔记 ｜ Layer Normalization》- 知乎
[2] 《Transformer论文逐段精读【论文精读】》- 李沐
[3] 《Transformer详解（李沐大神文字版，干货满满！）》- CSDN
[4] Regularization in Neural Networks
[5] About Train, Validation and Test Sets in Machine Learning

2.2.2 Scaled Dot-Product Attention

关于这部分的内容，核心问题应该有两个。

Q1:为什么Transformer搞了三个矩阵Q、K、V，然后一通操作猛如虎的就可以表示Attention注意力了？Q、K、V在这个过程中到底做了什么？
在看视频前，先从语文上分析注意力这个词语，先来一段你和妈妈的日常对话：“在外面一个人要多注意身体，工作是工作，不能把身体累垮了，身体是革命的本钱”，如果你比较注重自己的身体，那么这段话，我想会对你产生一些作用，你可能不自觉的会生成一个公式：
$$成功=0.3\times 事业+0.7\times 身体$$
当然，不同人的这个公式是不一样的，看你如何定义成功、成功包括哪些因素、这些因素所占权重又有多大，那么好，注意力的本质就是权重的分配，权重大点就多注意一些，权重少点就少注意一些。 其余内容由于本人表达与排版能力有限，请看本节参考视频[1]与[2]。

视频[1]还是没解释，为什么Q、K、V矩阵一样然后相乘也能表示注意力，看上去这并没有其视频开头提到的一些确切含义了。视频[2]及其弹幕提到了这些观点：
(1)Transformer中，不同head所拥有的Q矩阵负责不同种类的相关性。
(2)CNN经过特殊的构造，可以是Self-Attention的一个特例。
(3)RNN有长序列依赖问题和无法并行。

现在来解释$Q{K}^T$在干什么，先看到公式，
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$
我认为$Q{K}^T$和计算词向量之间的$cos$相似度并没有本质区别，$Q$矩阵第一行对应的词向量$q$与$K^T$矩阵第一列对应的词向量$k^T$相乘，有
$$cos(\theta )=\frac{q{k}^T}{|q||k^T|}$$
其余的行和列可以依次类推，看上去就和$cos$相似度差了一个系数而已。

Q2:自注意力机制中，为什么要除$\sqrt{d_k}$？又为什么要用softmax？
先看到计算公式
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$
也就是下面这张图的红框部分，Mask(opt.)是在说这个Mask是可选的，在Decoder架构中，会用到这个Mask，而Encoder里是没有这个Mask的。

图x —— Scaled Dot-Product Attention结构图

根据对$Softmax$的了解，一旦自变量x的值超过了一定区间，其斜率就变得平滑，无论x怎么变化，y值变化都不会太大，这样显然是没有什么区分度的，为了改善这种作用，因此加上了一个 $\sqrt{d_k}$ 的缩放因子，将自变量的取值区间落到一个合适的范围内，但你用$\sqrt{2d_k}$理论上可不可以呢？貌似没任何理由阻止你这样用，作者他们在文章给了个脚注，用来说明为什么用$\sqrt{d_k}$ 这个缩放因子，假设$q、k$互相独立，且$q、k$向量的数据遵从$mean=0,var=1$的分布，那么$q\cdot k={\sum }_{i=1}^{d_k}{q}_i{k}_i$的结果就遵从$mean=0,var=d_k$的分布，所以根据概率论知识，做一个$\sqrt{d_k}$的放缩，对方差有一个平方相乘的效果，于是结果就变回了$mean=0,var=1$的分布，具体可以再看看原文。但是，这又是什么新的教义？就因为$mean=0,var=1$听上去性质很不错？

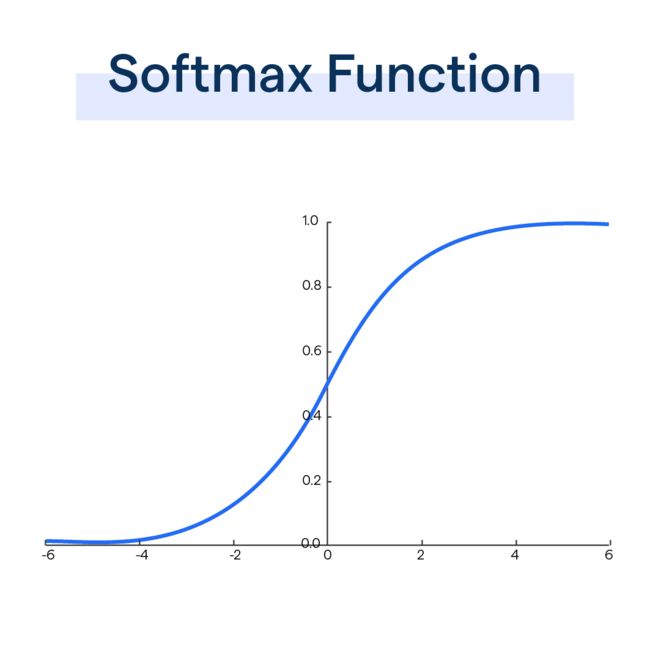
图x —— Softmax

讲完为什么要用$\sqrt{d_k}$，需要明白为什么要用softmax了，先读懂问题Q1，$softmax(?)$ 里的这个 $?$ 就是注意力的计算结果，也就是权重的大小，还是以例子来说明。
2016年12月14日，国家发展改革委印发通知——《国家发展改革委关于支持武汉建设国家中心城市的复函》^[4]，文件上是这么说武汉这座城市的，“具备建设国家中心城市的基础条件”，注意，没加重要二字，有网友是这么调侃的，重要的就是不重要，不强调重要就是重要^[5]，你可以理解为各城市的发展水平，就部分等价于引起上级机关对于各城市重要性的衡量程度，也就是心中的分量（权重无处不在）。那么转回来，注意力的计算结果就是发展水平，你可以简单理解为GDP，那么$softmax$就是上级机关在根据GDP计算每座城市在心中的分量的过程，从根本上说，$softmax$并不改变注意力计算的实质，只是做了一个归一化方便后面计算操作而已，李宏毅老师也在视频的26分30秒左右说，不一定要用$softmax$，有人把$softmax$换成$ReLU$结果还好一点^[2]。

额外问题:如何理解超参数？如何调超参数？
Transformer里的Attention head的数量就是个超参数，其实，模型需要的超参数是多少是没办法事先推断的，就像函数拟合，你说用二次函数拟合好呢，还是三次函数拟合好呢？两个拟合下来的方差可能都差不多，也没什么区别，但你事先就能知道要用二次或三次函数拟合吗？你可能是一个一个试出来的，就像炼丹一样，又遇到了一个先画靶子再射箭的例子。炼丹自从有了化学作为学科指导，就不再盲目，可以科学的制备化学品甚至预测化学性质；那么这个超参数，要遇到什么学科的出现，才能科学的推断超参数不再盲目呢？奥卡姆剃刀？奥卡姆剃刀不能用数学描述，又或者是，根据数据多训练几遍挑个好的不就知道了？那不行，化学可以根据化学式去推断性质甚至反推合成路线，怎么说最多也只能对数据做些分析，而不能真的拿网络去训练。这段完全胡说八道，如有不当，请各位看官指出。

2.2.2 参考文章或视频链接
[1] 【注意力机制的本质|Self-Attention|Transformer|QKV矩阵】- bilibili
[2] 【强烈推荐！台大李宏毅自注意力机制和Transformer详解！】- bilibili
[3] ML Lecture 14: Unsupervised Learning - Word Embedding
[4] 国家中心城市 - 百度百科
[5] 《科普:中心城市和重要的中心城市》- 百度贴吧
[6] 《超参数》- 百度贴吧
[7] Understanding Q,K,V In Transformer( Self Attention)

Attention is all you need 将Self-Attention发扬光大

2.2.3 Multi-Head Attention

这里的多头，就是把矩阵进行拆分，然后运算，然后再合并，这个过程高度类似于Hadoop的MapReduce，但是作用有所不同，不同的头在训练过程中，注意力观察的地方会不一样。诚所谓：“话说天下大势，合久必分，分久必合”，分治的思想贯穿人类始终，无论是政治架构还是地理格局。

在开始本章之前，还需要掌握两个事物：
(1)高维矩阵乘法：
2D矩阵与2D矩阵做矩阵乘法，得到的还是2D矩阵，但这是一个恰到好处的错觉。
所以你就天真地以为3D矩阵与3D矩阵做矩阵乘法，得到的还是3D矩阵？不对哦，根据参考文章[2]与[3]，得到的应该是一个4D矩阵。即$c_{jklm}=\sum _k{a}_{ijk}{b}_{klm}$，那4D矩阵呢？也符合这个规律吗，4D矩阵相乘还是4D矩阵。
(2)爱因斯坦求和约定：
请看参考文章[1]

2.2.3 参考文章或视频链接
[1] 《Einstein Summation (einsum) 的简单理解》- 知乎
[2] Multidimensional Matrix Mathematics:Multidimensional Matrix Equality, Addition,Subtraction, and Multiplication, Part 2 o
[3] Is there a 3-dimensional “matrix” by “matrix” product? - stackoverflow
[4] Understanding Numpy Matmul in 4D through Examples
[5] tensorflow中高维数组乘法运算 - 知乎
[6] 【全面理解多维矩阵运算】多维（三维四维）矩阵向量运算-超强可视化 - 知乎

2.3 Why Self-Attention

Why Self-Attention一章解释，为什么要自注意力呢？文章总结下来就是，计算词向量之间相关性的复杂度降低，提高并行度，对于解决long-range dependencies长序列依赖问题有奇效，

我记得19年软考有这么一道题目，计算两个矩阵相乘的时间复杂度，请看希赛网的解析。

2.3 参考文章或视频链接
[1] 《2019年上半年软考第65题》- 希赛题库

2.4 Training

Training，略，后续更新，请看原文，在学习率$lrate$上的这个公式有点奇怪，学习率也是根据一些参数计算出来的，另外也用到了$DropOut$，这也是常规操作了。

2.5 Results

Results重新强调了下结果，以及作者他们做的一些模型变种，就是调了参然后列了张表。

2.6 Conclusion

Conclusion 第一遍阅读的时候总结过了。