DFS和BFS经典例题总结1
文章目录
- 一、DFS
-
- I 员工的重要性
- II 被围绕的区域
- III 岛屿的周长、数量、最大面积
- IV 电话号码的字母组合
- V 二进制手表
- VI 子集、子集II
- VII 组合总和
- VII 验证二叉搜索树
- VIII 活字印刷
- VIII N皇后、N皇后II
- 二、BFS
-
- I 腐烂的橘子
- II 单词接龙
- III 价格范围内最高排名的 K 样物品
一、DFS
DFS是一种一条路走到黑的算法,如果一条路走到头了,则回溯到上个选择的点选择另一个方向继续走,直到遍历完图中所有的点。
从DFS的特性上我们就能看出,DFS的实现依靠回溯这一思想,在程序设计中,我们可以使用递归算法或依靠栈来实现DFS。
从DFS的概念中就能看出,这类算法会十分的暴力,它会遍历每一种情况,因此如果题目询问的问题是都有哪些可能并且需要把可能情况全部存起来返回时,DFS通常比较好用。
配合题目条件,有时可以进行一些“剪枝”,即把一些一定不可能的情况直接舍去,以此来减少算法的时间复杂度。
大致代码套路:
void DFS()
{
1.判断是否到达终点 如果到了就回溯上一层。
2.处理当前点
3.进行根据题意下一轮DFS
4.pop掉对当前点的处理,即回溯
}
I 员工的重要性
链接:员工的重要性

本题可以用深搜解决,也可以用宽搜解决,这里介绍深搜的做法。
每轮DFS中,我们根据id找到员工,让返回结果加上这位员工的重要性值,然后遍历它的下属id数组,进行下一轮DFS。
这里要多次通过id找到员工的指针,我们可以用一个哈希表以id为索引记录员工指针。
返回条件已经蕴含在遍历下属id数组中了,当某个下属的数组是空的时候,就会结束这一层函数然后往回返回了。
class Solution {
public:
unordered_map<int, Employee*> hash;
int ret = 0;
int getImportance(vector<Employee*> employees, int id)
{
for (auto e : employees)
{
hash[e->id] = e;
}
DFS(id);
return ret;
}
void DFS(int id)
{
auto employee = hash[id];
ret += employee->importance;
for (auto e : employee->subordinates)
{
DFS(e);
}
}
};
II 被围绕的区域
题目链接:被围绕的区域
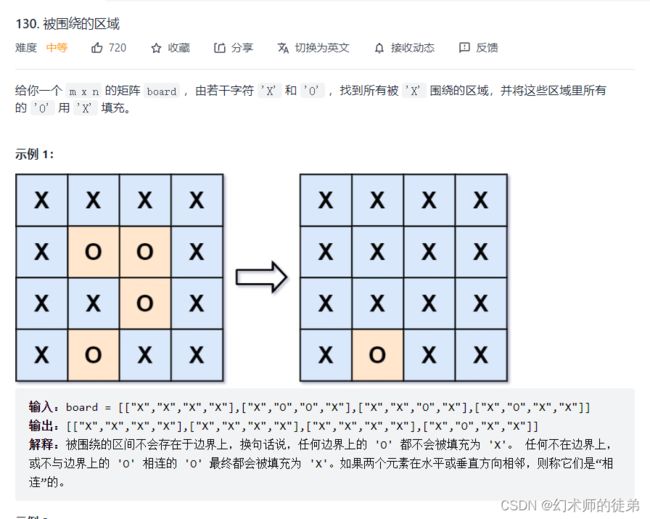
本题的难点在于想到:被X围绕的O区域一定是不与四条边上O连通的O,这里的连通指上下左右四个方向,否则这个区域和边界的O相连,一定不会被围绕。
想到这一点,本题的思路就明确了,遍历每个边界的O,利用DFS把与边界上的O相连通的O都改为另一个字符(比如’A’),这些’A’一定不是被围绕的’O’,然后把矩阵内的其他’O’改为’X’,然后把’A’改回‘O’即可。
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
void DFS(vector<vector<char>>& board, int x, int y)
{
int n = board.size();
int m = board[0].size();
board[x][y] = 'A';
for (int i = 0; i < 4; ++i)
{
int newx = x + dx[i];
int newy = y + dy[i];
if (newx < 0 || newx >= n || newy < 0 || newy >= m) continue;
if (board[newx][newy] == 'O') DFS(board, newx, newy);
}
}
void solve(vector<vector<char>>& board)
{
int n = board.size();
int m = board[0].size();
/*第一行和最后一行*/
for (int j = 0; j < m; ++j)
{
if (board[0][j] == 'O') DFS(board, 0, j);
if (board[n - 1][j] == 'O') DFS(board, n - 1, j);
}
/*第一列和最后一列*/
for (int i = 0; i < n; ++i)
{
if (board[i][0] == 'O') DFS(board, i, 0);
if (board[i][m - 1] == 'O') DFS(board, i, m - 1);
}
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
if (board[i][j] == 'O') board[i][j] = 'X';
else if (board[i][j] == 'A') board[i][j] = 'O';
}
}
}
};
本题也可以用多源宽搜来解决,先找到四个边界上的’O’点,然后开始宽搜染色。
III 岛屿的周长、数量、最大面积
链接:岛屿的周长

本题的关键在于找到一个岛屿点‘1’后,我们对这个点进行深搜。
如果遇到的是’1’点,那么继续深搜它周围的位置;
如果遇到了海水点’0’或出界了,注意到从岛屿点出界或遇到海水都会带来1的岛屿周长,注意把遍历过的岛屿点标记为’2’避免重复遍历。
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int islandPerimeter(vector<vector<int>>& grid)
{
int n = grid.size();
int m = grid[0].size();
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
if (grid[i][j] == 1) return DFS(grid, i, j);
}
}
return 0;
}
int DFS(vector<vector<int>>& grid, int x, int y)
{
/*出界带来一条边长 出界不可能重复*/
if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size())
return 1;
/*如果遇到海水点 也会带来一条边长*/
if (grid[x][y] == 0) return 1;
if (grid[x][y] == 2) return 0;/*标记过岛屿点的直接返回0 避免重复遍历*/
/*走到这里 说明遇到的是未标记过的岛屿点 标记避免重复遍历*/
grid[x][y] = 2;
int ret = 0;
for (int i = 0; i < 4; ++i)
{
ret += DFS(grid, x + dx[i], y + dy[i]);
}
return ret;
}
};
链接:岛屿的数量

本题的关键在于一次深搜会把与当前岛屿点相连的岛屿点都标记为2,然后循环时如果还能再遇到未遍历到的岛屿点‘1’,说明岛屿数量应该加1,能够进行的深搜的次数就是岛屿的数量。
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int numIslands(vector<vector<char>>& grid)
{
/*
每次搜索过程都把一块岛屿上的陆地'1'都修改成'0'
能进行多少次搜索说明有多少块陆地
*/
int ret = 0;
int n = grid.size();
int m = grid[0].size();
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
if (grid[i][j] == '1')
{
++ret;
DFS(grid, i, j);
}
}
}
return ret;
}
void DFS(vector<vector<char>>& grid, int x, int y)
{
grid[x][y] = '0';
for (int i = 0; i < 4; ++i)
{
int newx = x + dx[i];
int newy = y + dy[i];
if (newx >= 0 && newx < grid.size() && newy >= 0 && newy < grid[0].size()
&& grid[newx][newy] == '1') DFS(grid, newx, newy);
}
}
};
链接:岛屿的最大面积

有了上一题深搜的次数等于岛屿数量后,一次深搜的进行会覆盖一个岛屿,本题可以让每次深搜返回岛屿的点的个数,然后取大即可。
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid)
{
int n = grid.size();
int m = grid[0].size();
int ret = 0;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
ret = max(ret, DFS(grid, i, j));
}
}
return ret;
}
int DFS(vector<vector<int>>& grid, int x, int y)
{
if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size())
return 0;
if (grid[x][y] == 0 || grid[x][y] == 2) return 0;
grid[x][y] = 2;
return 1 + DFS(grid, x + 1, y) + DFS(grid, x, y + 1)
+ DFS(grid, x - 1, y) + DFS(grid, x, y - 1);
}
};
IV 电话号码的字母组合
链接:电话号码的字母组合

本题是典型的遍历所有情况的题目,用一个下标记录当前到达了什么位置,当到达终点时, 把字符串插入到结果中,对没轮情况,使用深搜注意回溯即可。
class Solution {
public:
vector<string> ret;
string curstr;
unordered_map<char, string> hash = {{'2', "abc"}, {'3', "def"}, {'4', "ghi"},
{'5', "jkl"}, {'6', "mno"}, {'7', "pqrs"}, {'8', "tuv"}, {'9', "wxyz"}};
vector<string> letterCombinations(string digits)
{
if (digits == "") return ret;
DFS(digits, 0);
return ret;
}
void DFS(const string& digits, int index)
{
if (index == digits.size())
{
ret.push_back(curstr);
return;
}
/*对当前位置的所有可能字符*/
for (auto ch : hash[digits[index]])
{
curstr.push_back(ch);
DFS(digits, index + 1);
curstr.pop_back();//回溯
}
}
};
V 二进制手表
本题其实可以枚举所有小时和分钟,然后对小时和分钟检查其二进制中1的个数即为亮灯的个数,如果亮灯的个数求和等于灯数,则此分钟合法,加到结果中。
但是如果我就是想用深搜做这个题也不是不可以,定义一个小时数组[1,2,4,8,0,0,0,0,0,0],再定义一个分钟数组[0,0,0,0,1,2,4,8,16,32],然后在DFS的参数中增加一个当前能够遍历的起始下标index,每轮都只能从当前起始下标index往后遍历,如果小时超过11或分钟超过59,则舍弃。
class Solution {
public:
/*找灯数的可能情况就是找这两个数组对应个数元素的子集*/
int Hour[10] = {1, 2, 4, 8, 0, 0, 0, 0, 0, 0};
int Minute[10] = {0, 0, 0, 0, 1, 2, 4, 8, 16, 32};
vector<string> ret;
vector<string> readBinaryWatch(int turnedOn)
{
DFS(turnedOn, 0, 0, 0);
return ret;
}
void DFS(int CanOpen, int hour, int minute, int index)
{
if (hour > 11 || minute > 59) return;
if (CanOpen == 0)
{
string s = to_string(hour) + ':'
+ (minute < 10 ? '0' + to_string(minute) : to_string(minute));
ret.push_back(s);
}
for (int i = index; i < 10; ++i)
{
DFS(CanOpen - 1, hour + Hour[i], minute + Minute[i], i + 1);
}
}
};
VI 子集、子集II
题目链接:子集
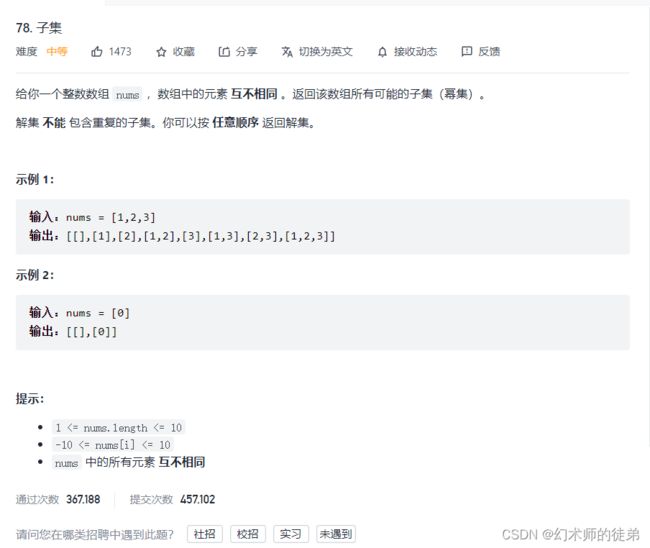
要获得子集,同样也是一种“遍历所有情况”的问题方式,选择使用DFS,在参数中增加一个当前遍历到的下标数,对每个下标对应的元素,我们可以选择让它如此轮的子集集合,也可以让它不入此轮的子集集合。
返回条件为下标走到了终点,注意入集合后需要回溯pop。
class Solution {
public:
vector<vector<int>> ret;
vector<int> cur;
vector<vector<int>> subsets(vector<int>& nums)
{
DFS(nums, 0);
return ret;
}
void DFS(const vector<int>& nums, int index)
{
if (index == nums.size())
{
ret.push_back(cur);
return;
}
/*不放*/
DFS(nums, index + 1);
/*放*/
cur.push_back(nums[index]);
DFS(nums, index + 1);
cur.pop_back();
}
};
题目链接:子集II
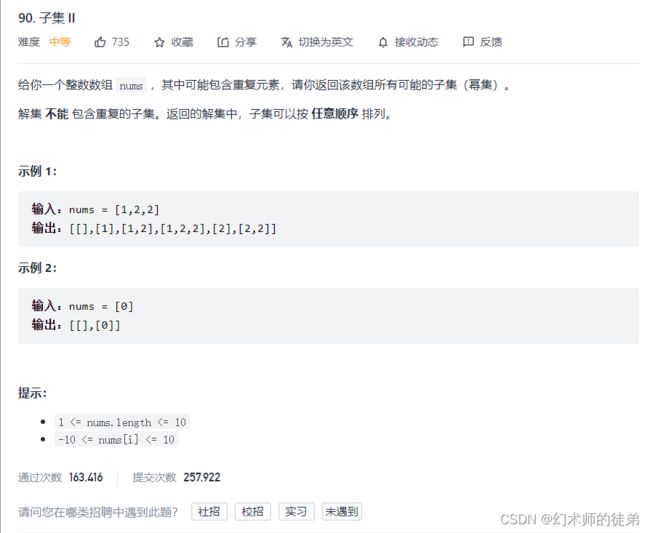
本题的关键在于集合中有重复元素,但是组成出来的子集不准有重复的,如[1,2]和[1,2],所以可以考虑先把数组排序,这样相同的元素就会相邻,什么情况下会从[1,2,2]中出现[1,2(2)]和[1,2(3)]这种相同的子集呢?
注意到如果我们没选前一个元素且前一个元素和当前元素相等,也就是选择[1]后选择2(3)的时候,没选2(2),在上一次选2(2)的时候已经形成了一轮子集插入了,此时再选2(3)再形成的一系列子集一定会与上一轮重复,于是此时直接返回,进行“剪枝”。
class Solution {
public:
vector<vector<int>> ret;
vector<int> curset;
vector<vector<int>> subsetsWithDup(vector<int>& nums)
{
sort(nums.begin(), nums.end());
DFS(nums, 0, false);
return ret;
}
void DFS(const vector<int>& nums, int index, bool chooseprev)
{
if (index == nums.size())
{
ret.push_back(curset);
return;
}
/*不选当前元素*/
DFS(nums, index + 1, false);
/*选当前元素*/
if (!chooseprev && index > 0 && nums[index - 1] == nums[index])
return;
curset.push_back(nums[index]);
DFS(nums, index + 1, true);
curset.pop_back();
}
};
VII 组合总和
链接:组合总和
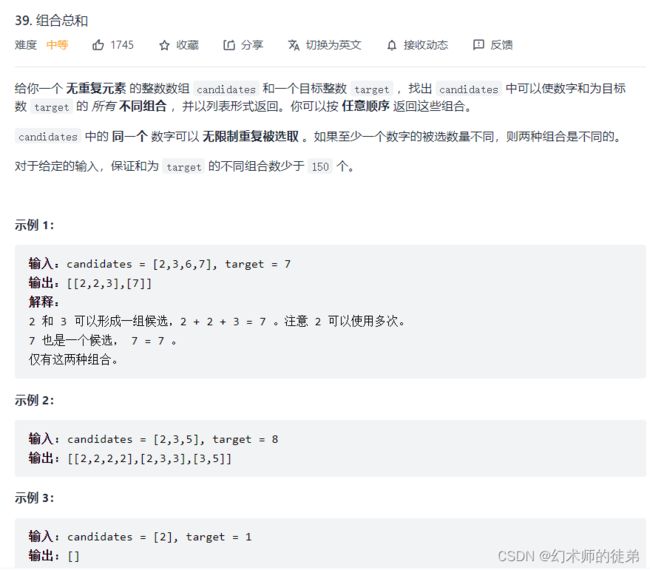
本题的关键在于不要取到相同的组合,比如不要取得[2,3,3]和[3,2,3],观察可知不取得相同的组合的方法是每次都取自己或自己往后的元素,不要往前取。
class Solution {
public:
vector<vector<int>> ret;
vector<int> curset;
vector<vector<int>> combinationSum(vector<int>& candidates, int target)
{
DFS(candidates, target, 0);
return ret;
}
void DFS(const vector<int>& candidates, int target, int index)
{
if (target < 0 || index == candidates.size()) return;
if (target == 0)
{
ret.push_back(curset);
return;
}
DFS(candidates, target, index + 1);
/*选当前位置*/
if (target - candidates[index] >= 0)
{
curset.push_back(candidates[index]);
DFS(candidates, target - candidates[index], index);
curset.pop_back();
}
}
};
向后看也可以模仿二进制手表,把代码写成这样:
class Solution {
public:
vector<vector<int>> ret;
vector<int> curset;
vector<vector<int>> combinationSum(vector<int>& candidates, int target)
{
DFS(candidates, target, 0, 0);
return ret;
}
void DFS(const vector<int>& candidates, int target, int curval, int index)
{
if (curval > target) return;
if (curval == target)
{
ret.push_back(curset);
return;
}
for (int i = index; i < candidates.size(); ++i)
{
curset.push_back(candidates[i]);
DFS(candidates, target, curval + candidates[i], i);
//DFS(candidates, target, curval + candidates[i], i + 1);
curset.pop_back();
}
}
};
VII 验证二叉搜索树
链接:验证二叉搜索树
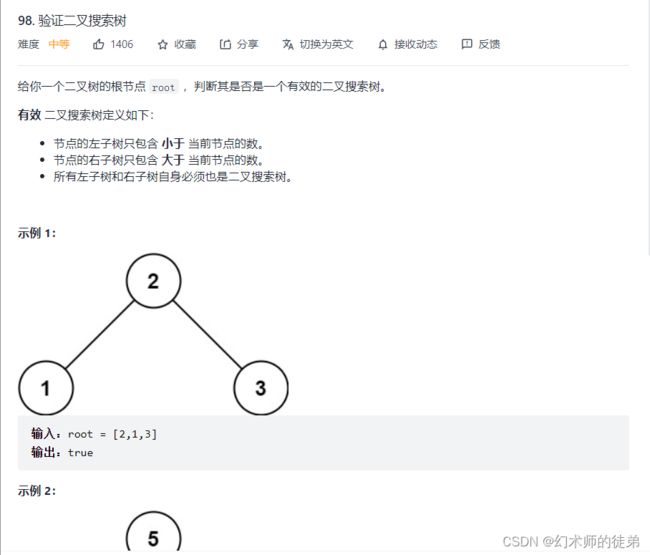
其实本题并不算非常典型的DFS,不过树的前序、中序、后续遍历也算一种DFS,所以这里把本题也并做DFS。
BST的性质是它的中序遍历的过程会形成一个递增的序列,因此只要我们在中序遍历的过程中记录前继结点,每次中序遍历遍历自己结点时比较一下前继结点和自己结点是否满足递增关系即可。
class Solution {
public:
TreeNode* prev = nullptr;
bool isValidBST(TreeNode* root)
{
if (root == nullptr) return true;
if (!isValidBST(root->left)) return false;
if (prev != nullptr)
{
if (prev->val >= root->val) return false;
}
prev = root;
return isValidBST(root->right);
}
};
VIII 活字印刷
链接:活字印刷

本题和之前的题就有所不同了,在本题中,"AB"和"BA"是不同的,所以本题每次选择时都可以要从最头上选择以保证不同顺序,又因为本题有每个字符只能选择一次的限制,所以本题还得增加一个是否选过了的数组。
但是这样选仍然可能选出重复情况,因为本题的字母是可以重复的,因此我们可以使用一个哈希集合来去重。
class Solution {
public:
unordered_set<string> hashset;
bool used[8] = {0};
int numTilePossibilities(string tiles)
{
string curstr;
DFS(tiles, curstr);
return hashset.size();
}
void DFS(const string& tiles, string& curstr)
{
/*非空就是一种排列情况*/
if (!curstr.empty())
{
hashset.insert(curstr);
/*
这里没必要return 因为接下来还可以插入别的元素
*/
}
for (int i = 0; i < tiles.size(); ++i)
{
if (used[i] == false)
{
used[i] = true;
curstr += tiles[i];
DFS(tiles, curstr);
curstr.pop_back();
used[i] = false;
}
}
}
};
VIII N皇后、N皇后II
链接:N皇后

当某一位置摆了一个皇后过后,同一行、同一列、同一正对角线、同一斜对角线都不能再摆放皇后。
从题目特性可以看出,本题可以采用深搜加回溯的算法,对同一行不能摆放皇后的限制,我们可以每次都遍历不同行,对同一列、同一正对角线、同一反对角线不能摆放皇后的限制,我们可以储存当前已经摆放过的皇后的下标,同一列即y坐标相同,同一正对角线即x-y相等,同一反对角线即x+y相等,
class Solution {
public:
/*记录当前布局的每个点的坐标 用于判断是否冲突*/
vector<pair<int, int>> check;
vector<vector<string>> ret;
vector<string> curset;
vector<vector<string>> solveNQueens(int n)
{
/*先把布局初始化成n*n的'.'*/
string s(n, '.');
curset = vector<string>(n, s);
DFS(n, 0);
return ret;
}
void DFS(int n, int row)
{
/*如果能走到最后一行 则把当前布局插入答案中*/
if (row == n)
{
ret.push_back(curset);
return;
}
/*
判断当前行的每一列是否可以插入皇后
如果可以 则当前布局插入皇后并且把该点入到check中
进行下一行 然后回溯
如果都不能 走到结尾自动回到上一层
*/
for (int j = 0; j < n; ++j)
{
bool state = true;
for (auto e : check)
{
if (j == e.second || j + row == e.first + e.second
|| j - row == e.second - e.first)
{
state = false;
break;
}
}
if (state == true)
{
check.push_back({row, j});
curset[row][j] = 'Q';
DFS(n, row + 1);
curset[row][j] = '.';
check.pop_back();
}
}
}
};
链接:N皇后II

本题只要把上题中的可能情况并入答案中的过程改为记录可能情况数+1即可。
class Solution {
public:
vector<pair<int, int>> check;
int ret = 0;
int totalNQueens(int n)
{
DFS(n, 0);
return ret;
}
void DFS(const int n, int row)
{
if (row == n){
++ret;
return;
}
for (int j = 0; j < n; ++j)
{
bool state = true;
for (auto e : check)
{
if (j == e.second || row + j == e.first + e.second
|| row - j == e.first - e.second)
{
state = false;
break;
}
}
if (state == true)
{
check.push_back({row, j});
DFS(n, row + 1);
check.pop_back();
}
}
}
};
二、BFS
宽度有限搜索是每次都同时遍历当前结点的相邻结点,这样一层一层的遍历。
与深度优先搜索不同,宽搜可以解决一些最短距离问题,因为宽搜每次都是按照规则向周围各走一步,如果某层遍历到了目标那么此时的层数就是最短的步数。
宽度有限搜索需要队列来辅助实现。
宽搜处理同一层以获得步数(距离)的模板:
void BFS()
{
queue q;
int step = 0;
起始位置入队列 且标记起始位置已用过
while (!q.empty())
{
//获得当前队列元素个数 处理同一层
int size = q.size();
while (size--)
{
处理当前位置
判断当前位置相邻位置能否入队列
}
++step;//当前层处理完了 步数加1
}
}
I 腐烂的橘子
本题较好的处理方法是多源宽度有限搜索。
首先遍历一遍矩阵把所有腐烂的橘子入到队列中,以这些期初就已经腐烂的橘子为源,开始宽搜,使用记录步数的模板,每次先把队列中的个数取出,然后处理这些个数个队列的元素,然后再让步数+1。
最后遍历一遍矩阵,如果矩阵中没有好的橘子了,那么就返回步数,否则返回-1表示无法把所有的橘子都腐烂掉。
这里正好用腐烂的橘子的标记2,每次只感染新的橘子1,使得不能重复遍历。
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int orangesRotting(vector<vector<int>>& grid)
{
/*
先把所有坏掉的橘子入队
每次让队列中保留当前宽度优先遍历的最外层
最外层就是这一秒将会污染别的橘子的坏橘子
如果队列空了后 矩阵中还有好橘子 则返回-1
否则返回宽度优先遍历的步数
*/
queue<pair<int, int>> q;
int n = grid.size();
int m = grid[0].size();
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
if (grid[i][j] == 2) q.push({i, j});
}
}
int step = 0;
while (!q.empty())
{
int size = q.size();
bool check = false;
while (size--)
{
auto e = q.front();
q.pop();
for (int i = 0; i < 4; ++i)
{
int newx = e.first + dx[i];
int newy = e.second + dy[i];
if (newx < 0 || newx >= n || newy < 0 || newy >= m)
continue;
if (grid[newx][newy] == 1)
{
grid[newx][newy] = 2;
q.push({newx, newy});
check = true;
}
}
}
if (check == true)
{
/*说明这步有往外走*/
++step;
}
}
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
if (grid[i][j] == 1) return -1;
return step;
}
};
II 单词接龙
链接:单词接龙

这个题也是个宽搜模板题,一样利用宽搜处理步数,每次处理元素时,先检查它是否和endWord相同,如果相同就返回步数,否则让它只变一个位置的字符,然后查询变化后的单词是否在词典中,如果在,则让它入队列,并且标记该单词已经用过了,否则不做处理。
由于本题要经常查询单词是否在词典中,所以本题可以使用一个哈希集合把词典中的单词都储存起来,这样查询操作就是 O ( 1 ) O(1) O(1)的了。
至于如果标记单词已经用过了,同样可以用一个哈希集合,这样查找的效率更高一些。
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList)
{
unordered_set<string> dic;/*因为后续要查找词典 用哈希集合效率高一点O(1)*/
unordered_set<string> used;/*如果在集合中 则说明已经该单词用过了*/
int step = 1;/*因为要返回序列长度 所以一开始的步长设为1为好*/
queue<string> q;
for (auto wd : wordList)
{
dic.insert(wd);
}
q.push(beginWord);
while (!q.empty())
{
int size = q.size();/*每次只看当前层的 这样方便记录步数*/
while (size--)
{
auto e = q.front();
q.pop();
if (e == endWord) return step;
for (int i = 0; i < e.size(); ++i)
{
for (char ch = 'a'; ch <= 'z'; ++ch)
{
char tmp = e[i];
e[i] = ch;
if (dic.find(e) != dic.end() && used.find(e) == used.end())
{
q.push(e);
used.insert(e);
}
e[i] = tmp;
}
}
}
++step;
}
return 0;/*如果在上面都没有返回,说明无法通过词典变成endWord 返回0*/
}
};
III 价格范围内最高排名的 K 样物品
这是第70届双周赛的第三题,本题要处理步数,因此脱不开宽搜。
具体就是先判断出发位置是否为障碍物,如果是,则直接返回;否则把出发位置入队列,标记出发位置已经遍历过了,然后同样处理同一步的这些位置,判断这些位置的价值是否在价值区间中,如果在则把(距离,价值,横坐标,纵坐标)入到待排序集合中(这里也可以用优先级队列),然后处理它周围的点,判断周围的点是否能通过下一步到达(未使用过、且不为障碍物),如果能到达,则让它入队列作为下一步的节点处理。
处理完当前层的结点后,++step,接着处理下一层的结点。
class Solution {
public:
vector<vector<int>> ret;
vector<tuple<int, int, int, int>> set;
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
vector<vector<int>> highestRankedKItems(vector<vector<int>>& grid, vector<int>& pricing, vector<int>& start, int k)
{
/*注意边界情况 不要设置只能入k个 同一层的可能有更有价值的*/
if (grid[start[0]][start[1]] == 0) return ret;
int n = grid.size();
int m = grid[0].size();
int low = pricing[0];
int high = pricing[1];
int step = 0;
vector<vector<bool>> used(n, vector<bool>(m));
used[start[0]][start[1]] = true;
queue<pair<int, int>> q;
q.push({start[0], start[1]});
while (!q.empty())
{
int size = q.size();
while (size--)
{
auto e = q.front();
q.pop();
int val = grid[e.first][e.second];
if (val >= low && val <= high)
{
set.push_back({step, val, e.first, e.second});
}
for (int i = 0; i < 4; ++i)
{
int newx = e.first + dx[i];
int newy = e.second + dy[i];
if (newx < 0 || newx >= n || newy < 0 || newy >= m ||
used[newx][newy] == true || grid[newx][newy] == 0)
{
continue;
}
used[newx][newy] = true;
q.push({newx, newy});
}
}
++step;
}
sort(set.begin(), set.end(), cmp());
/*注意k有可能超出set内元素个数 导致越界*/
int l = min(k, (int)set.size());
for (int i = 0; i < l; ++i)
{
auto [d, val, x, y] = set[i];
ret.push_back({x, y});
}
return ret;
}
struct cmp
{
bool operator()(const tuple<int, int, int, int>& t1,
const tuple<int, int, int, int>& t2)
{
auto [d1, val1, x1, y1] = t1;
auto [d2, val2, x2, y2] = t2;
if (d1 != d2) return d1 < d2;
if (val1 != val2) return val1 < val2;
if (x1 != x2) return x1 < x2;
if (y1 != y2) return y1 < y2;
return true;
}
};
};


