LeetCode刷题复盘笔记——77. 组合 && 216. 组合总和 III（一文搞懂回溯解决组合问题）

今日主要总结一下，77. 组合 && 216. 组合总和 III

题目：77. 组合

Leetcode题目地址

题目描述：
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

本题重难点

本题这是回溯法的经典题目。

直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出和示例中一样的结果。
如果n为100，k为50呢，那就50层for循环，是不是开始窒息。

此时就会发现虽然想暴力搜索，但是用for循环嵌套连暴力都写不出来！当遇到for循环暴力搜索都搜不出来的情况时就可以考虑使用回溯算法了，回溯法就用递归来解决嵌套层数的问题。
递归来做层叠嵌套（可以理解是开k层for循环），每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了。
此时递归的层数大家应该知道了，例如：n为100，k为50的情况下，就是递归50层。

也这样说不太容易直观理解，其实回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了。

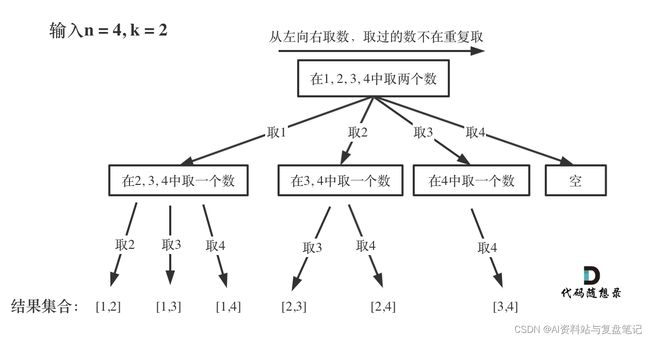
那么我把组合问题抽象为如下树形结构：

图中可以发现n相当于树的宽度，k相当于树的深度。
那么如何在这个树上遍历，然后收集到我们要的结果集呢？
图中每次搜索到了叶子节点，我们就找到了一个结果。

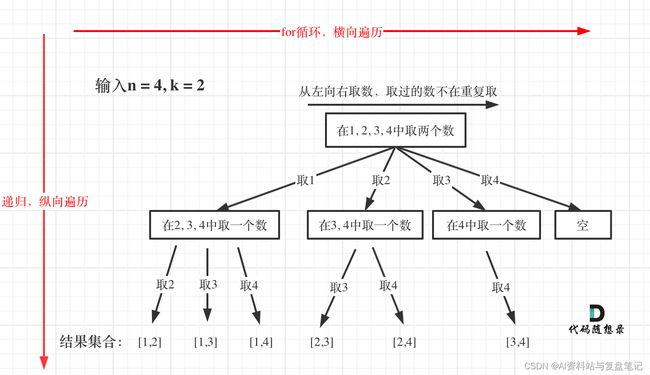
回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

一、未优化解法

C++代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    void backtracing(int n, int k, int startIndex){
        if(path.size() == k){
            res.push_back(path);
            return;
        }
        for(int i = startIndex; i <= n; i++){
            path.push_back(i);
            backtracing(n, k, i + 1);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        path.clear();
        backtracing(n, k, 1);
        return res;
    }
};

二、优化解法

优化思路

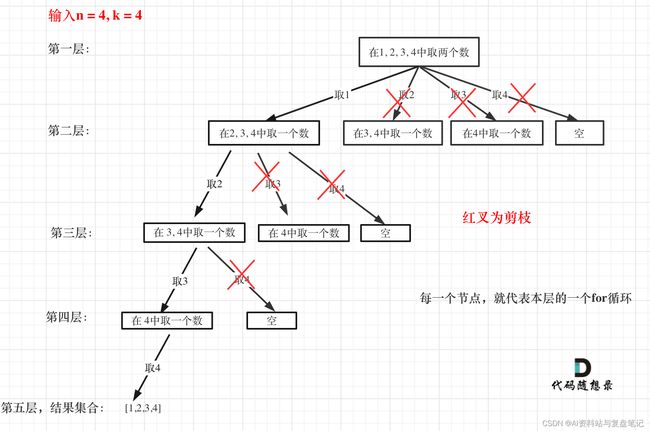
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

优化过程如下：

已经选择的元素个数：path.size();

所需需要的元素个数为: k - path.size();

列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size()）

在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。实在还不懂可以举个例子动手画一下

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

C++代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    void backtracing(int n, int k, int startIndex){
        if(path.size() == k){
            res.push_back(path);
            return;
        }
        for(int i = startIndex; i <= n - (k - path.size()) + 1; i++){//优化
            path.push_back(i);
            backtracing(n, k, i + 1);
            path.pop_back();
        }
        return;
    }
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        path.clear();
        backtracing(n, k, 1);
        return res;
    }
};

题目二：216. 组合总和 III

Leetcode题目地址

题目描述：
找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9

每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

2 <= k <= 9
1 <= n <= 60

本题重难点

本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。

相对于77. 组合 ，无非就是多了一个限制，本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,…,9]。所以我们在回溯递归函数backtracing形参中再加一个sum变量来记录目前已经在组合里面的和为多少就可以了

递归终止条件就改成在满足path.size() == k 的基础上，满足sum == n就可以了

一、正确解法

C++代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    void backtracing(int n, int k, int sum, int start){
        if(sum > n) return;
        if(path.size() == k){
            if(sum == n){
                res.push_back(path);
            }
        }
        for(int i = start; i <= 9 - (k - path.size()) + 1; i++){
            sum += i;
            path.push_back(i);
            backtracing(n, k, sum, i + 1);
            path.pop_back();
            sum -= i;
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        path.clear();
        res.clear();
        backtracing(n, k, 0, 1);
        return res;
    }
};

总结

此时就会发现虽然想暴力搜索，但是用for循环嵌套连暴力都写不出来！当遇到for循环暴力搜索都搜不出来的情况时就可以考虑使用回溯算法了，回溯法就用递归来解决嵌套层数的问题。
递归来做层叠嵌套（可以理解是开k层for循环），每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了。

这两道题做完大家可以做一下40. 组合总和 II
这道题，或者看一下一文搞懂回溯解决有重集合中结果去重的组合问题我对这道题有详细的讲解

---

欢迎大家关注本人公众号：编程复盘与思考随笔

(关注后可以免费获得本人在csdn发布的资源源码)

公众号主要记录编程和刷题时的总结复盘笔记和心得！并且分享读书、工作、生活中的一些思考感悟！