背包问题

1 01背包

1.1 基础

问题：物品重量weight[i],  价值value[i], 求容量为bagweight的背包，能装物品的最大价值？

1.1.1 二维数组 

1.1.1.1 n行二维数组

dp[i][j] 

表示从下标为[0,i]的物品中任意选取，放入容量为j的背包，最大价值

递推公式

对于物品i,有两种情况：

• 放不下：dp[i][j] = dp[i-1][j],  等价于从下标为[0,i-1]的物品中任意选取，放入容量为j的背包，最大价值
• 放得下：dp[i][j] = dp[i-1][j-weight[i]] + value[i]，dp[i-1][j-weight[i]] 为在背包容量减去物品i的重量的情况下,在[0,i-1]范围选择物品，可以存放的最大价值。                                                 dp[i][j]取最大值，dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

初始化

当容量j为0，dp[i][0] = 0

当i=0，j>=weight[0]时，dp[0][j] = value[0]; 否则，dp[0][j] = 0

遍历顺序

dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])，不管先遍历物品还是背包容量，dp[i][j]运算所需数据都在dp[i][j]的左上角，所以先遍历物品或者背包容量都可以。

先遍历物品：

先遍历背包容量：

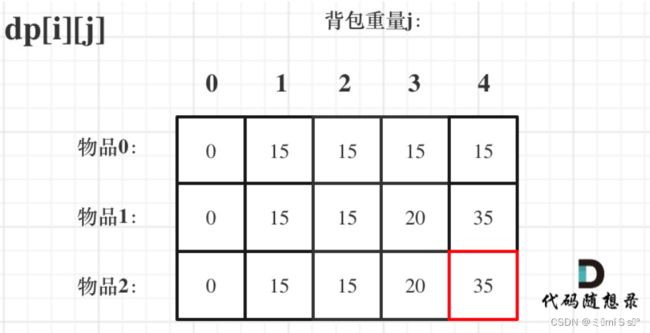
举例推导 

 代码

int n;          //物品数量
int bagweight;  //背包空间
 
void func(){
    vector weight(n,0);    //每个物品的重量
    vector value(n,0);     //每个物品的价值
     
    for(int i=0;i> weight[i];
    for(int i=0;i> value[i];
         
    vector> dp(n, vector(bagweight+1, 0));
     
    for(int j=0;j=weight[0]时，dp[0][j] = value[0]
    for(int j=weight[0];j<=bagweight;++j)
        dp[0][j] = value[0];
     
    //遍历物品
    for(int i=1;i

 1.1.1.1 n+1行二维数组

初始化

计算最大容量，全初始化为0；计算次数、种类，第一个元素初始化为1

代码

int n;          //物品数量
int bagweight;  //背包空间
 
void func(){
    vector weight(n,0);    //每个物品的重量
    vector value(n,0);     //每个物品的价值
     
    for(int i=0;i> weight[i];
    for(int i=0;i> value[i];
         
    vector> dp(n+1, vector(bagweight+1, 0));
     
     
    //遍历物品
    for(int i=1;i<=n;++i){
        int w = weight[i-1];
        int v = value[i-1];
        
        //遍历背包容量
        for(int j=0;j<=bagweight;++j){
            if(j < w)   //不放物品i
                dp[i][j] = dp[i-1][j];
            else
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + v);
        }
    }
     
    cout << dp[n][bagweight] << endl;
}

1.1.2 一维滚动数组

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

dp[j]

背包容量为j的情况下，可以存放的物品的最大价值

递推公式

dp[j] = max(dp[j], dp[j-weight[i]] + value[i])

二维：dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

dp[j]相当于dp[i-1][j]，是上一层的数据。外层遍历物品，内层遍历背包容量。如果从小到大遍历背包容量，那么更大的j所需要的上层数据会被当前层数据覆盖掉，因此要从大到小遍历背包容量。

并且只遍历到weight[i]，如果背包容量

初始化

与n+1行二维数组相同。计算最大容量，全初始化为0；计算次数、种类，第一个元素初始化为1。

遍历顺序

外层遍历物品，内层遍历背包容量。

如果从小到大遍历背包容量，那么更大的j所需要的上层数据会被当前层数据覆盖掉，导致的结果是同一物品可能被放入多次，情况如下：

遍历当前背包容量，选择放物品i的情况下，dp[j] = dp[j-weight[i]] + value[i]，而dp[j-weight[i]]如果被当前层数据覆盖掉（在容量为j-weight[i]的情况下选择放物品i），同一物品就会被放入多次。

因此要从大到小遍历背包容量。

那可不可以先遍历背包容量？不可以。

一维数组的情况下，背包容量一定是倒序遍历的，避免覆盖上层数据。如果外层遍历背包容量且倒序遍历，那么dp[j]需要的前面的数据dp[j-weight[i]]还是初始化的状态，结果一定不对。如果正序遍历背包容量就不会存在这中问题。

举例推导

代码 

int n;  //物品数量
int bagweight;  //背包空间
 
void func(){
    vector weight(n,0);
    vector value(n,0);
     
    for(int i=0;i> weight[i];
    for(int i=0;i> value[i];
     
    vector dp(bagweight+1, 0);
     
    for(int i=0; i=weight[i]; --j){
            dp[j] = max(dp[j], dp[j-weight[i]] + value[i]);
        }
    }
     
    cout << dp[bagweight] << endl;
     
}