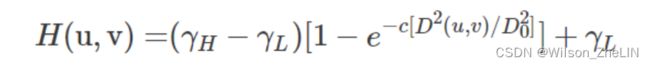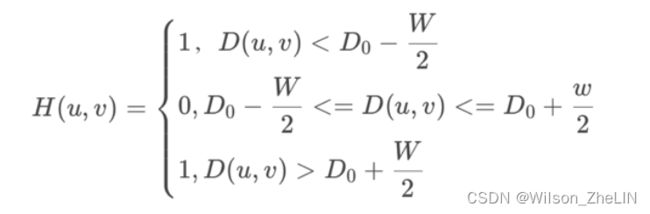C语言数字图像处理(七):图像噪声&降噪算法,同态滤波器和带阻滤波器
0. 完整仓库 & 教程:
这一章节的完整代码在:Chapter 7. Image Noise and Noise Reduction
如果你喜欢这个系列的文章或者感觉对你有帮助,请给我的仓库一个⭐️。
1. 同态滤波器
算法:
同态滤波器的过程与第六章(这部分可以参考:6:低通滤波器和高通滤波器)中的高通/低通滤波器类似:
首先对图像进行二维离散傅里叶变换 DFT (这部分原理需要理解: 5: 二维离散傅里叶变换和重建),得到每个像素的复数数组。 每个复数的实部和虚部分别乘以 (, )。 (, ) 的公式为:
其中 > 1, < 1,并且 ![]() 表示通带的半径。 (, )的计算方法也是两点之间的距离,通过公式:
表示通带的半径。 (, )的计算方法也是两点之间的距离,通过公式:
其中 和 是图像的长和宽。在后续的代码处理中,设置 = 1.5, = 0.75, ![]() = 30, = 1。
= 30, = 1。
图像和结果对比(bridge, goldhill):
结果分析:
同态滤波本质上是频域滤波器(frequency domain filter),它结合了频率滤波和空间灰度变换。 通常,图像的亮部(illumination)是缓慢变化的部分,集中在低频部分。 反射部分(reflection)属于快速变化的部分,往往集中在高频部分。
这里选用模型的形状类似于一个逆高斯滤波器(见章节6),可以减弱低频分量(illumination)的影响并强调高频分量(reflection)。 最终的结果是压缩了动态范围和增强了对比度,使纹理更加突出。
代码实现(完整代码见顶部GitHub):
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
float H = (1.5 - 0.75) * (1 - pow(M_E, pow(dis / 30, 2) * -1)) + 0.75;
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
printf("Homomorphic Finished!\n");
outimage = iDFT(image, real, imaginary);这里再把第5章里傅里叶变换和重建的代码搬过来下:
void DFT(Image *image, float *real_array, float *imaginary_array) {
unsigned char *tempin, *tempout;
float real, imaginary;
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing function");
tempin = image->data;
tempout = outimage->data;
printf("DFT algorithm is executing...\n");
for(int i = 0; i < image->Height; i++) {
for(int j = 0; j < image->Width; j++) {
real = 0;
imaginary = 0;
for(int m = 0; m < image->Height; m++) {
for(int n = 0; n < image->Width; n++) {
float temp = (float)i * m / (float)image->Height + (float)j * n / (float)image->Width;
int offset = (m + n) % 2 == 0 ? 1 : -1;
real += tempin[image->Width * m + n] * cos(-2 * pi * temp) * offset;
imaginary += tempin[image->Width * m + n] * sin(-2 * pi * temp) * offset;
}
}
real_array[image->Width * i + j] = real;
imaginary_array[image->Width * i + j] = imaginary;
int temp = (int)(sqrt(real*real + imaginary*imaginary) / sqrt((float)image->Height*(float)image->Width));
if(temp < 0) temp = 0;
if(temp > 255) temp = 255;
tempout[image->Width * i + j] = temp;
}
}
printf("DFT Finished!\n");
SavePNMImage(outimage, (char*)"DFT.pgm");
}
Image *iDFT(Image *image, float *real_array, float *imaginary_array) {
unsigned char *tempin, *tempout;
float real;
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing function");
tempin = image->data;
tempout = outimage->data;
printf("iDFT algorithm is executing...\n");
for(int i = 0; i < image->Height; i++) {
for(int j = 0; j < image->Width; j++) {
real = 0;
for (int m = 0; m < image->Height; m++){
for (int n = 0; n < image->Width; n++){
float temp = (float)i * m / (float)image->Height + (float)j * n / (float)image->Width;
real += real_array[image->Width * m + n] * cos(2 * pi * temp) - imaginary_array[image->Width * m + n] * sin(2 * pi * temp);
}
}
int offset = (i + j) % 2 == 0 ? 1 : -1;
int temp = (int)(real / ((float)image->Height*(float)image->Width) * offset);
if(temp < 0) temp = 0;
if(temp > 255) temp = 255;
tempout[image->Width * i + j] = temp;
}
}
printf("iDFT Finished!\n");
return (outimage);
}2. 添加正弦噪声 & 使用带阻滤波器恢复:
算法:
(1)添加正弦噪声算法:
其中 是幅度,、 分别是相对于 x 和 y 轴确定的正弦频率。
(2)带阻滤波器:
根据对噪声图像的光谱分析,我们可以看到噪声分布在中心周围。 所以我们需要一个滤波器,能够阻止某些频率范围内的信号通过,而允许其他频率范围内的信号通过:
其中 是环形带的宽度。 所以过滤器的原理会是这样的:
图像和结果对比(lena):
结果分析:
可以看到周期性噪声分布在频谱图的中心周围。 因此,我们可以根据噪声分布的位置和距离构造带阻滤波器,以阻止这些频率范围内的信号通过来降噪。 重建后的图像也恢复正常了。 然而,与理想低通滤波器类似,其带边界变化过于陡峭,因此可能会引起一定的振铃现象。
代码实现(完整代码见顶部GitHub):
(1)加正弦噪声:
for(int i = 0; i < image->Height; i++) {
for(int j = 0; j < image->Width; j++) {
float noise = 20 * (sin(i * 40) + sin(j * 40));
tempout[image->Height * i + j] = tempin[image->Height * i + j] + noise;
}
}(2)带阻滤波器:
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
float H;
if(dis > 75 && dis < 110) H = 0;
else H = 1;
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
printf("Bandreject Filter Finished!\n");
outimage = iDFT(image, real, imagi3. 图像降噪
3.1 图像:LenaWithNoise
算法:
“LenaWithNoise”的图像中包含“水平扫描线”。 从DFT光谱中我们发现其中心存在垂直信号脉冲,因此我们想要隔离掉这些噪声以改善图像。 故考虑垂直陷波抑制滤波器(vertical notch reject filter),如下所示(白色=1,黑色=0):
图像和结果对比(LenaWithNoise):
结果分析:
这种周期性干扰相对容易消除。 通过在垂直轴上隔离频率,处理后的结果与原始图像相比有了很大的改善。
代码实现(完整代码见顶部GitHub):
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
float H;
if(j > 240 && j < 246 && dis >= 45) H = 0;
else H = 1;
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
outimage = iDFT(image, real, imaginary);3.2 图像:cameraWithNoise
算法:
选择的方法:自适应均值滤波器
定义::掩码中的最小值,:掩码中的最大值,:掩码中的中心值,:掩码中的中值。
自适应中值滤波器有两个处理过程,分别记为:A和B。
A:
![]()
![]()
![]()
![]()
B:
![]()
![]()
![]()
![]()
图像和结果对比(cameraWithNoise):
结果分析:
画面中有零星的黑白点,明显属于椒盐噪声类型。 对于椒盐噪声比较合适的方式是中值滤波,但是经过实践,发现自适应滤波器的效果更好,因为它的细节保留表现和降噪效果更好。
与传统中值滤波器相比,自适应中值滤波器能够更好地保护图像中的边缘细节。 因为它会检查掩模(卷积)中的中心像素和中值像素是否是噪声。
代码实现(完整代码见顶部GitHub):
void AdaptiveMedian(Image *image) {
unsigned char *tempin, *tempout, Sudoku[9], enlarge[25];
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing Function");
tempin = image->data;
tempout = outimage->data;
for(int i = 1; i < image->Height-1; i++) {
for(int j = 1; j < image->Width-1; j++){
int num = 0;
for(int x = -1; x <= 1; x++) {
for(int y = -1; y <= 1; y++) {
Sudoku[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
// Use Insertion Sort:
for(int m = 1; m < 9; m++) {
int currNum = Sudoku[m];
int n = m;
while(n >= 1 && Sudoku[n-1] > currNum) {
Sudoku[n] = Sudoku[n-1];
n--;
}
Sudoku[n] = currNum;
}
// Case 1: the median one is not a noise:
if(Sudoku[0] < Sudoku[4] && Sudoku[4] < Sudoku[8]) {
// check whether the current central pixel is a noise:
int temp = tempin[image->Height * i + j];
if(Sudoku[0] < temp && temp < Sudoku[8]) tempout[image->Height * i + j] = temp;
else tempout[image->Height * i + j] = Sudoku[4];
}
// Case 2: the median one is a noise, so expand the mask:
else {
int num = 0;
for(int x = -2; x <= 2; x++) {
for(int y = -2; y <= 2; y++) {
enlarge[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
// Use Insertion Sort:
for(int m = 1; m < 25; m++) {
int currNum = enlarge[m];
int n = m;
while(n >= 1 && enlarge[n-1] > currNum) {
enlarge[n] = enlarge[n-1];
n--;
}
enlarge[n] = currNum;
}
// check whether the current central pixel is a noise:
int temp = tempin[image->Height * i + j];
if(enlarge[0] < temp && temp < enlarge[8]) tempout[image->Height * i + j] = temp;
else tempout[image->Height * i + j] = enlarge[12];
}
}
}
SavePNMImage(outimage, (char*)"AdaptiveMedian.pgm");
}4. 五种降噪算法对比分析
算法:
(1)算术平均滤波器:
图片中的每个像素(除了边缘处)都被八个像素包围, 我们通过取 九个像素的平均值来重新计算每个像素的值。 算法为:
(2)几何平均滤波器:
算法改为:
(3)中值滤波器:
与算术均值滤波器类似,但每个像素的值被掩模的中值代替,而不是平均值。 我将 9 个包围像素的值存储到一个数组中,并使用插入排序方法找到其中位数 [4],它将分配给 (, )。
(4) Alpha-trimmed均值滤波器:
修改后的alpha均值滤波器去除最高值和最低值,即对过滤范围内的数据进行排序,按照从大到小的顺序去除个数据,按照从小到大的顺序去除个数据,计算剩余数据的均值。
(5) 自适应均值滤波器:
同上面3.2部分的算法
图像和结果对比(lenaD1, D2, D3):
结果分析:
图像D1被高斯噪声污染,图像D2被椒盐噪声污染,图像D3被高斯噪声和椒盐噪声混合污染。
- 算术均值滤波对高斯噪声和椒盐噪声影响不大,但同时会对图像进行平滑处理。
- 几何均值滤波器在处理高斯噪声和盐噪声时比算术均值滤波器损失的图像细节要少,但它根本无法处理胡椒噪声。
- 中值滤波对高斯噪声有一定的效果,擅长处理椒盐噪声,并且与算术均值滤波相比会保留更多的细节。
- Alpha-trimmed均值滤波器擅长去除受椒盐噪声以及其他类型噪声污染的图像中的噪声。
- 自适应均值滤波器具有总体最佳的降噪性能,尤其是椒盐噪声。 与普通中值滤波器相比,它还能更好地保护图像中的边缘细节。
代码实现(完整代码见顶部GitHub):
(1)算术平均滤波器:
for(int i = 1; i < image->Height-1; i++) {
for(int j = 1; j < image->Width-1; j++){
int num = 0;
for(int x = -1; x <= 1; x++) {
for(int y = -1; y <= 1; y++) {
Sudoku[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
int sum = 0;
for(int k = 0; k < 9; k++) {
sum += Sudoku[k];
}
sum /= 9;
if(sum > 255) sum = 255;
if(sum < 0) sum = 0;
tempout[image->Height * i + j] = sum;
}
}(2)几何平均滤波器:
for(int i = 1; i < image->Height-1; i++) {
for(int j = 1; j < image->Width-1; j++){
int num = 0;
for(int x = -1; x <= 1; x++) {
for(int y = -1; y <= 1; y++) {
Sudoku[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
float product = 1.0;
for(int k = 0; k < 9; k++) {
product *= Sudoku[k];
}
product = pow(product, 1.0/9.0);
int temp = product;
if(temp > 255) temp = 255;
if(temp < 0) temp = 0;
tempout[image->Height * i + j] = temp;
}
}(3)中值滤波器:
for(int i = 1; i < image->Height-1; i++) {
for(int j = 1; j < image->Width-1; j++){
int num = 0;
for(int x = -1; x <= 1; x++) {
for(int y = -1; y <= 1; y++) {
Sudoku[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
// Use Insertion Sort:
for(int m = 1; m < 9; m++) {
int currNum = Sudoku[m];
int n = m;
while(n >= 1 && Sudoku[n-1] > currNum) {
Sudoku[n] = Sudoku[n-1];
n--;
}
Sudoku[n] = currNum;
}
tempout[(image->Width)*i + j] = Sudoku[4];
}
}(4) Alpha-trimmed均值滤波器:
for(int i = 1; i < image->Height-1; i++) {
for(int j = 1; j < image->Width-1; j++){
int num = 0;
for(int x = -1; x <= 1; x++) {
for(int y = -1; y <= 1; y++) {
Sudoku[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
// Use Insertion Sort:
for(int m = 1; m < 9; m++) {
int currNum = Sudoku[m];
int n = m;
while(n >= 1 && Sudoku[n-1] > currNum) {
Sudoku[n] = Sudoku[n-1];
n--;
}
Sudoku[n] = currNum;
}
// set the d/2 to 2:
int sum = 0, d = 2;
for(int k = d; k < 9-d; k++) {
sum += Sudoku[k];
}
sum /= 9 - 2 * d;
if(sum > 255) sum = 255;
if(sum < 0) sum = 0;
tempout[image->Height * i + j] = sum;
}
}(5)自适应均值滤波器:
void AdaptiveMedian(Image *image) {
unsigned char *tempin, *tempout, Sudoku[9], enlarge[25];
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing Function");
tempin = image->data;
tempout = outimage->data;
for(int i = 1; i < image->Height-1; i++) {
for(int j = 1; j < image->Width-1; j++){
int num = 0;
for(int x = -1; x <= 1; x++) {
for(int y = -1; y <= 1; y++) {
Sudoku[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
// Use Insertion Sort:
for(int m = 1; m < 9; m++) {
int currNum = Sudoku[m];
int n = m;
while(n >= 1 && Sudoku[n-1] > currNum) {
Sudoku[n] = Sudoku[n-1];
n--;
}
Sudoku[n] = currNum;
}
// Case 1: the median one is not a noise:
if(Sudoku[0] < Sudoku[4] && Sudoku[4] < Sudoku[8]) {
// check whether the current central pixel is a noise:
int temp = tempin[image->Height * i + j];
if(Sudoku[0] < temp && temp < Sudoku[8]) tempout[image->Height * i + j] = temp;
else tempout[image->Height * i + j] = Sudoku[4];
}
// Case 2: the median one is a noise, so expand the mask:
else {
int num = 0;
for(int x = -2; x <= 2; x++) {
for(int y = -2; y <= 2; y++) {
enlarge[num++] = tempin[(image->Width)*(i+x) + (j+y)];
}
}
// Use Insertion Sort:
for(int m = 1; m < 25; m++) {
int currNum = enlarge[m];
int n = m;
while(n >= 1 && enlarge[n-1] > currNum) {
enlarge[n] = enlarge[n-1];
n--;
}
enlarge[n] = currNum;
}
// check whether the current central pixel is a noise:
int temp = tempin[image->Height * i + j];
if(enlarge[0] < temp && temp < enlarge[8]) tempout[image->Height * i + j] = temp;
else tempout[image->Height * i + j] = enlarge[12];
}
}
}
SavePNMImage(outimage, (char*)"AdaptiveMedian.pgm");
}5. 完整代码
这一章节的完整代码在:Chapter 7. Image Noise and Noise Reduction
更多关于数字图像处理的章节,以及所有的原图像在:Introduction to Digital Image Processing
整理代码、翻译原理,和可视化每一个章节的工作非常耗时耗力,并且不会有任何收入和回报。如果你喜欢这个系列的文章或者感觉对你有帮助,请给我的仓库一个⭐️,这将是对独立作者最大的鼓励。
-END-