GAMES101-现代计算机图形学入门-闫令琪 课程笔记 - 汇总(上)
一些前言与感慨:
GAMES真的是一个很好的平台,GAMES101也真的是很好的课
可惜当年在学校里学计算机图形学的时候,还没有闫令琪这么好的课程,当时学得一知半解,云里雾里,希望一切重新拾起还不算太晚。
GAMES在线课程背景:
2019年下半年,GAMES执行委员会常委会刘利刚老师和周晓巍老师开始讨论规划 在GAMES平台上开设系列图形学及相关领域的在线课程,目的是激发广大学生对图形学的热爱、降低图形学的入门门槛、推广和推动图形学学科发展。
2019年11月,刘利刚老师在澳大利亚布里斯班举行的Siggraph Asia大会上遇到加州大学圣芭芭拉分校的闫令琪老师,并一起讨论在GAMES上开设在线课程的想法及未来规划,一拍即合。于是决定邀请闫令琪老师在次年春节后开设计算机图形学入门基础课程。
2020年1月,新冠肺炎疫情开始肆虐全球。在春节之后,闫令琪老师于2020年2月17日开始开设GAMES 101在线课程《现代计算机图形学入门》。
之后,刘利刚老师邀请了麻省理工大学的胡渊鸣同学于2020年6月1日开始开设GAMES 201在线课程《高级物理引擎实战指南2020》。
根据常委会老师的自荐及推荐,随后一年内的3门在线课程也规划好了,分别为:2020年10月-12月的刘利刚老师的GAMES 102《几何建模与处理基础》、2021年2月-5月闫令琪老师的GAMES 202《高质量实时渲染》、2021年6月-8月黄其兴老师的GAME 203《三维视觉和理解》,并于2020年10月3日发出在线课程预告。
2020年10月11日,刘利刚老师开始开设GAMES 102《几何建模与处理基础》在线课程。
GAMES101 11周的课程,值得用 C++和 OpenGL 好好写一写代码
学了计算机图形学,人会感慨数学公式和世界的奇妙,之前学的概率论、线性代数、高数、信号处理等,在这里统统用上了。时常觉得世界一定有一个很强大的运算器,才可以把真实世界渲染得这么完美,天衣无缝,没有bug.
文章目录
- 0 介绍
- 1 向量与线性代数
-
- 向量的计算
-
- 点乘(dot/scalar product)
- 叉乘(cross/vector product)
- 在内部
-
- 坐标系
- 矩阵乘法
- 2 变换
-
- 2维变换
-
- 缩放
- 斜切
- 旋转
- 齐次坐标
-
- 平移变换
- 仿射变换
-
- 缩放
- 旋转
- 平移
- 组合变换
- 逆变换
-
- 旋转
- 三维变换
-
- 缩放
- 平移
- 旋转
-
- 齐次坐标
- 欧拉角
- 观测变换(viewing)
-
- view/camera transformation 视图变换
- projection transformation 投影变换
-
- Orthographic projection 正交投影
- perspective projection 透视投影
- 3 光栅化
-
- 锯齿问题
- 抗锯齿
- 滤波
- 深度测试 Z-buffer
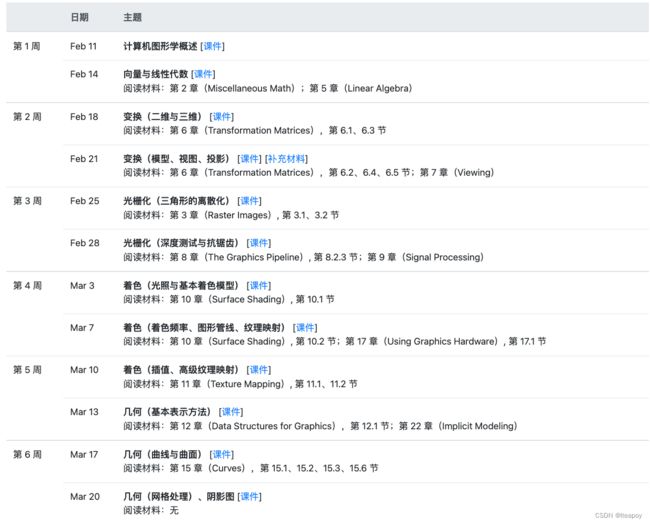
0 介绍
- 课程主页
- 计算机图形学与混合现实在线平台GAMES
- GAMES101-现代计算机图形学入门-闫令琪
- 课程笔记
- 课程笔记
- 作业链接
光线追踪 - 慢,常用于电影中,生成效果好,一般离线使用
有实时光线追踪算法
- 不讲 shaders
- OpenGL / DirectX / Vulcan 属于 API,不会教如何做
- 不会教你使用 unity / unreal 引擎
总的大纲:
- 向量与线性代数、变换(二维、三维)、变换(模型、视图、投影)
- 光栅化(三角形的离散化、深度测试与抗锯齿)
- 着色
- 几何
- 光线追踪
- 材质与外观
1 向量与线性代数
向量:方向和长度,不关心绝对的起始位置
向量长度
单位向量
向量求和:平行四边形法则,三角形法则
代数上,直接求和
向量的计算
点乘(dot/scalar product)
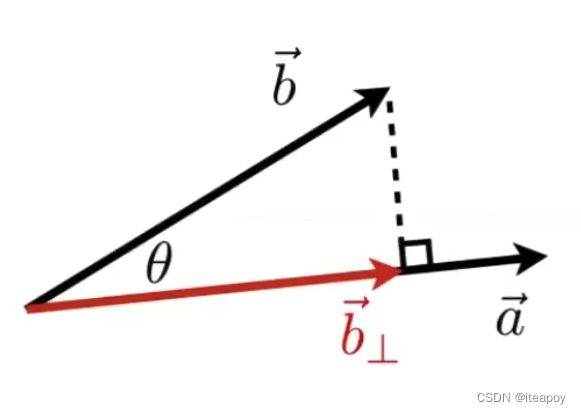
- a ⃗ ⋅ b ⃗ = ∥ a ⃗ ∥ ∥ b ⃗ ∥ cos θ \vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta a⋅b=∥a∥∥b∥cosθ
- cos θ = a ⃗ ⋅ b ⃗ ∥ a ⃗ ∥ ∥ b ⃗ ∥ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|} cosθ=∥a∥∥b∥a⋅b
- 当两个向量都是单位向量时, cos θ = a ^ ⋅ b ^ \cos \theta=\hat{a} \cdot \hat{b} cosθ=a^⋅b^
- 性质:
- 交换律: a ⃗ ⋅ b ⃗ = b ⃗ ⋅ a ⃗ \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} a⋅b=b⋅a
- 分配律: a ⃗ ⋅ ( b ⃗ + c ⃗ ) = a ⃗ ⋅ b ⃗ + a ⃗ ⋅ c ⃗ \vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} a⋅(b+c)=a⋅b+a⋅c
- 结合律: ( k a ⃗ ) ⋅ b ⃗ = a ⃗ ⋅ ( k b ⃗ ) = k ( a ⃗ ⋅ b ⃗ ) (k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b}) (ka)⋅b=a⋅(kb)=k(a⋅b)
- 在笛卡尔坐标系下:
- 2维: a ⃗ ⋅ b ⃗ = ( x a y a ) ⋅ ( x b y b ) = x a x b + y a y b \vec{a} \cdot \vec{b}=\left(\begin{array}{l}x_a \\ y_a\end{array}\right) \cdot\left(\begin{array}{l}x_b \\ y_b\end{array}\right)=x_a x_b+y_a y_b a⋅b=(xaya)⋅(xbyb)=xaxb+yayb
- 3维: a ⃗ ⋅ b ⃗ = ( x a y a z a ) ⋅ ( x b y b z b ) = x a x b + y a y b + z a z b \vec{a} \cdot \vec{b}=\left(\begin{array}{c}x_a \\ y_a \\ z_a\end{array}\right) \cdot\left(\begin{array}{c}x_b \\ y_b \\ z_b\end{array}\right)=x_a x_b+y_a y_b+z_a z_b a⋅b= xayaza ⋅ xbybzb =xaxb+yayb+zazb
- 图形学中的应用:
叉乘(cross/vector product)
- 叉乘后的向量垂直于 a 和b 的向量组成的平面 a × b = − b × a a \times b=-b \times a a×b=−b×a(不满足交换律)
- 大小: ∥ a × b ∥ = ∥ a ∥ b ∥ sin ϕ \|a \times b\|=\|a\| b \| \sin \phi ∥a×b∥=∥a∥b∥sinϕ
- 方向:右手定则(从a旋转到b的方向)(openGL API里是左手系)
- 性质:
- x ⃗ × y ⃗ = + z ⃗ \vec{x} \times \vec{y}=+\vec{z} x×y=+z
- y ⃗ × x ⃗ = − z ⃗ \vec{y} \times \vec{x}=-\vec{z} y×x=−z
- y ⃗ × z ⃗ = + x ⃗ \vec{y} \times \vec{z}=+\vec{x} y×z=+x
- z ⃗ × y ⃗ = − x ⃗ \vec{z} \times \vec{y}=-\vec{x} z×y=−x
- z ⃗ × x ⃗ = + y ⃗ \vec{z} \times \vec{x}=+\vec{y} z×x=+y
- x ⃗ × z ⃗ = − y ⃗ \vec{x} \times \vec{z}=-\vec{y} x×z=−y
- a ⃗ × b ⃗ = − b ⃗ × a ⃗ \vec{a} \times \vec{b}=-\vec{b} \times \vec{a} a×b=−b×a
- a ⃗ × a ⃗ = 0 → \vec{a} \times \vec{a}=\overrightarrow{0} a×a=0(长度为0的向量)
- 分配律: a ⃗ × ( b ⃗ + c ⃗ ) = a ⃗ × b ⃗ + a ⃗ × c ⃗ \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} a×(b+c)=a×b+a×c
- 结合律: a ⃗ × ( k b ⃗ ) = k ( a ⃗ × b ⃗ ) \vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b}) a×(kb)=k(a×b)
- 代数
- a ⃗ × b ⃗ = ( y a z b − y b z a z a x b − x a z b x a y b − y a x b ) \vec{a} \times \vec{b}=\left(\begin{array}{c}y_a z_b-y_b z_a \\ z_a x_b-x_a z_b \\ x_a y_b-y_a x_b\end{array}\right) a×b= yazb−ybzazaxb−xazbxayb−yaxb
- 可以表示成矩阵的形式: a ⃗ × b ⃗ = A ∗ b = ( 0 − z a y a z a 0 − x a − y a x a 0 ) ( x b y b z b ) \vec{a} \times \vec{b}=A^* b=\left(\begin{array}{ccc}0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{array}\right)\left(\begin{array}{l}x_b \\ y_b \\ z_b\end{array}\right) a×b=A∗b= 0za−ya−za0xaya−xa0 xbybzb
- 应用:
-
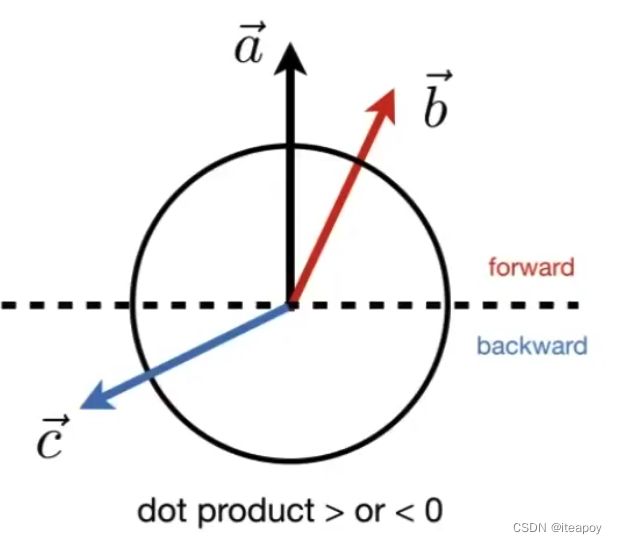
判定左右
- b 在 a 的左还是右?
- a 叉乘 b
- 得到正值,则 b 在 a 左侧
- 得到负值,则 b 在 a 的右侧
-
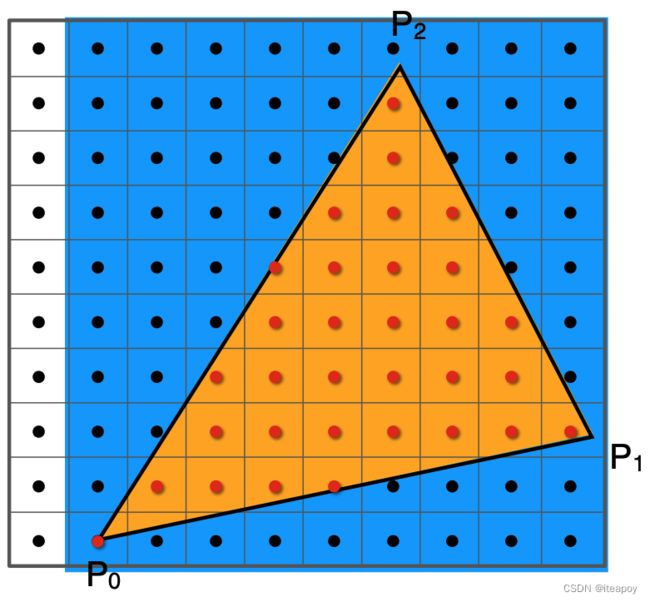
判定内外(光栅化的基础,对内部的点进行着色)
-
在内部
- 点 ABC 逆时针排列
- AB 叉乘 AP,正数,P在AB左侧
- BC 叉乘 BP,正数,P在BC左侧
- CA 叉乘 CP,正数,P在CA左侧
- 如果不确定点 ABC是顺时针还是逆时针
- P 一定都在 AB、BC、CA 的左边或者右边,否则在外部
- 为0的时候,可以说在里面,也可以说在外面(corner case)
- 点 ABC 逆时针排列
-
-
坐标系
- 任意三个向量,如果满足以下条件,则构成一个直角坐标系
- ∥ u ⃗ ∥ = ∥ v ⃗ ∥ = ∥ w ⃗ ∥ = 1 \|\vec{u}\|=\|\vec{v}\|=\|\vec{w}\|=1 ∥u∥=∥v∥=∥w∥=1
- u ⃗ ⋅ v ⃗ = v ⃗ ⋅ w ⃗ = u ⃗ ⋅ w ⃗ = 0 \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0 u⋅v=v⋅w=u⋅w=0
- w ⃗ = u ⃗ × v ⃗ \vec{w}=\vec{u} \times \vec{v} \quad w=u×v (right-handed)
- 任意一个向量,分解到这个直角坐标系中,用投影相加
- p ⃗ = ( p ⃗ ⋅ u ⃗ ) u ⃗ + ( p ⃗ ⋅ v ⃗ ) v ⃗ + ( p ⃗ ⋅ w ⃗ ) w ⃗ \vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w} p=(p⋅u)u+(p⋅v)v+(p⋅w)w
矩阵乘法
- 矩阵变换:移动、旋转、缩放、错切
- 性质:
- 没有交换律
- 结合律: ( A B ) C = A ( B C ) (A B) C=A(B C) (AB)C=A(BC)
- 分配律:
- A ( B + C ) = A B + A C A(B+C)=A B+A C A(B+C)=AB+AC
- ( A + B ) C = A C + B C (A+B) C=A C+B C (A+B)C=AC+BC
- 性质:
- 矩阵的转置
- 行和列交换
- ( 1 2 3 4 5 6 ) T = ( 1 3 5 2 4 6 ) \left(\begin{array}{ll}1 & 2 \\ 3 & 4 \\ 5 & 6\end{array}\right)^T=\left(\begin{array}{lll}1 & 3 & 5 \\ 2 & 4 & 6\end{array}\right) 135246 T=(123456)
- 性质: ( A B ) T = B T A T (A B)^T=B^T A^T (AB)T=BTAT
- 行和列交换
- 单位矩阵
- 对角阵
- 矩阵互逆:
- A A − 1 = A − 1 A = I A A^{-1}=A^{-1} A=I AA−1=A−1A=I
- 性质: ( A B ) − 1 = B − 1 A − 1 (A B)^{-1}=B^{-1} A^{-1} (AB)−1=B−1A−1
- 用矩阵的形式表示向量的计算
- 点乘: a ⃗ ⋅ b ⃗ = a ⃗ T b ⃗ = ( x a y a z a ) ( x b y b z b ) = ( x a x b + y a y b + z a z b ) \vec{a} \cdot \vec{b}=\vec{a}^T \vec{b}=\left(\begin{array}{lll}x_a & y_a & z_a\end{array}\right)\left(\begin{array}{c}x_b \\ y_b \\ z_b\end{array}\right)=\left(x_a x_b+y_a y_b+z_a z_b\right) a⋅b=aTb=(xayaza) xbybzb =(xaxb+yayb+zazb)
- 叉乘: a ⃗ × b ⃗ = A ∗ b = ( 0 − z a y a z a 0 − x a − y a x a 0 ) ( x b y b z b ) \vec{a} \times \vec{b}=A^* b=\left(\begin{array}{ccc}0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{array}\right)\left(\begin{array}{l}x_b \\ y_b \\ z_b\end{array}\right) a×b=A∗b= 0za−ya−za0xaya−xa0 xbybzb (向量 a ⃗ \vec{a} a 的对偶矩阵 A ∗ A^* A∗)
2 变换
-
用途:
- 模型变换(modeling)
- 视图变换(viewing)
- 三维投影到二维(视图发生变化)
-
MVP 变换:model transformation -> view transformation -> projection transformation
2维变换
- 线性变换:
- x ′ = a x + b y x^{\prime}=ax+by x′=ax+by
- y ′ = c x + d y y^{\prime}=cx+dy y′=cx+dy
- [ x ′ y ′ ] = [ a b c d ] [ x y ] \left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] [x′y′]=[acbd][xy]
- 用矩阵表示
缩放
-
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] = [ s x x s y y ] \left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}s_x & 0 \\ 0 & s_y\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] = \left[\begin{array}{l}s_x x \\ s_y y\end{array}\right] [x′y′]=[sx00sy][xy]=[sxxsyy]
-
沿着 y 轴的反射:KaTeX parse error: Unknown column alignment: m at position 191: …[\begin{array}{m̲} -x \\ y \end…
斜切
- [ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] \left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}1 & a \\ 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] [x′y′]=[10a1][xy]
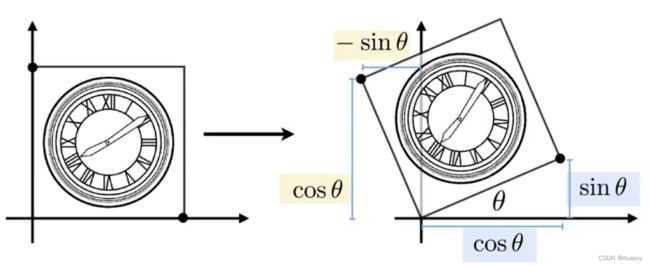
旋转
- 旋转矩阵: R θ = [ cos θ − sin θ sin θ cos θ ] \mathbf{R}_\theta=\left[\begin{array}{cc}\textcolor{#7785aa}{\cos \theta} & \textcolor{#e4da9a}{-\sin \theta} \\ \textcolor{#7785aa}{\sin \theta} & \textcolor{#e4da9a}{\cos \theta} \end{array}\right] Rθ=[cosθsinθ−sinθcosθ]
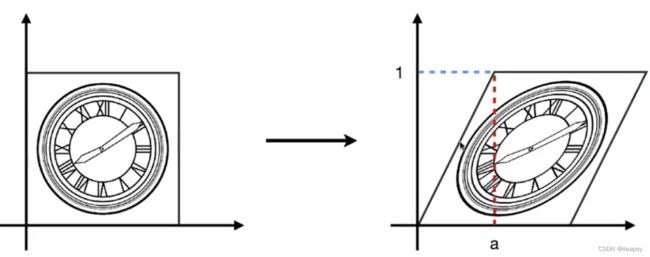
齐次坐标
平移变换
-
平移变换不属于线性变换!!!
- Q:如何用一种统一的方法来表示?
- A:二维的向量增加一个维度,变成三维的(引入齐次变换)
- 二维的点: ( x , y , 1 ) T \left(\mathbf{x}, \mathbf{y}, \textcolor{red}{1}\right)^{\mathrm{T}} (x,y,1)T
- 二维的向量: ( x , y , 0 ) T \left(\mathbf{x}, \mathbf{y}, \textcolor{red}{0}\right)^{\mathrm{T}} (x,y,0)T - 向量具有平移不变性
- 验证其有效性:
- 向量 + 向量 = 向量
- 点 - 点 = 向量
- 点 + 向量 = 点
- 点 + 点 = 两个点的中点(扩充的定义) - ( x y w ) \left(\begin{array}{l}x \\ y \\ w \end{array}\right) xyw 相当于 ( x w y w 1 ) \left(\begin{array}{l}\frac{x}{w} \\ \frac{y}{w} \\ 1 \end{array}\right) wxwy1 此处 w ≠ 0 w\neq 0 w=0
-
( x ′ y ′ ) = ( x y ) + ( t x t y ) \left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)=\left(\begin{array}{l}x \\ y\end{array}\right)+\left(\begin{array}{l}t_x \\ t_y\end{array}\right) (x′y′)=(xy)+(txty)
-
( x ′ y ′ w ′ ) = ( 1 0 t x 0 1 t y 0 0 1 ) ⋅ ( x y 1 ) = ( x + t x y + t y 1 ) \left(\begin{array}{c}x^{\prime} \\ y^{\prime} \\ w^{\prime}\end{array}\right)=\left(\begin{array}{llc}1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1\end{array}\right) \cdot\left(\begin{array}{l}x \\ y \\ 1\end{array}\right)=\left(\begin{array}{c}x+t_x \\ y+t_y \\ 1\end{array}\right) x′y′w′ = 100010txty1 ⋅ xy1 = x+txy+ty1
仿射变换
-
仿射变换 = (先) 线性变换 + (再) 平移变换
- 在二维仿射变换情况下,最后一行都是 0 0 1
-
( x ′ y ′ ) = ( a b c d ) ⋅ ( x y ) + ( t x t y ) \left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right) \cdot\left(\begin{array}{l}x \\ y\end{array}\right)+\left(\begin{array}{l}t_x \\ t_y\end{array}\right) (x′y′)=(acbd)⋅(xy)+(txty)
等价于
- ( x ′ y ′ 1 ) = ( a b t x c d t y 0 0 1 ) ⋅ ( x y 1 ) \left(\begin{array}{c}x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{llc}a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1\end{array}\right) \cdot\left(\begin{array}{l}x \\ y \\ 1\end{array}\right) x′y′1 = ac0bd0txty1 ⋅ xy1
缩放
- S ( s x , s y ) = ( s x 0 0 0 s y 0 0 0 1 ) S(s_x, s_y) = \left(\begin{array}{llc} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1\end{array}\right) S(sx,sy)= sx000sy0001
旋转
- R ( α ) = ( cos α − sin α 0 sin α cos α 0 0 0 1 ) R(\alpha) = \left(\begin{array}{llc} \cos\alpha & -\sin\alpha & 0 \\ \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 1\end{array}\right) R(α)= cosαsinα0−sinαcosα0001
平移
- T ( t x , t y ) = ( 1 0 t x 0 1 t y 0 0 1 ) T(t_x, t_y) = \left(\begin{array}{llc} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1\end{array}\right) T(tx,ty)= 100010txty1
组合变换
-
平移、旋转、缩放变换可以组合起来
-
变换的顺序很重要,不能调换(矩阵的乘法不满足交换律)
- e.g. T ( 1 , 0 ) ⋅ R 45 ≠ R 45 ⋅ T ( 1 , 0 ) T_{(1,0)} \cdot R_{45} \neq R_{45} \cdot T_{(1,0)} T(1,0)⋅R45=R45⋅T(1,0)
-
可以通过矩阵的乘法来实现组合变换,从右到左的操作
- A n ( … A 2 ( A 1 ( x ) ) ) = A n ⋯ A 2 ⋅ A 1 ⋅ ( x y 1 ) A_n\left(\ldots A_2\left(A_1(\mathbf{x})\right)\right)=\mathbf{A}_n \cdots \mathbf{A}_2 \cdot \mathbf{A}_1 \cdot\left(\begin{array}{l}x \\ y \\ 1\end{array}\right) An(…A2(A1(x)))=An⋯A2⋅A1⋅ xy1
- e.g. 先旋转 45度,再平移 (1, 0)
- T ( 1 , 0 ) ⋅ R 45 [ x y 1 ] = [ 1 0 1 0 1 0 0 0 1 ] [ cos 4 5 ∘ − sin 4 5 ∘ 0 sin 4 5 ∘ cos 4 5 ∘ 0 0 0 1 ] [ x y 1 ] = [ cos 4 5 ∘ − sin 4 5 ∘ 1 sin 4 5 ∘ cos 4 5 ∘ 0 0 0 1 ] [ x y 1 ] T_{(1,0)} \cdot R_{45}\left[\begin{array}{c}x \\ y \\ 1\end{array}\right]=\left[\begin{array}{lll}1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}\cos 45^{\circ} & -\sin 45^{\circ} & 0 \\ \sin 45^{\circ} & \cos 45^{\circ} & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y \\ 1\end{array}\right] = \left[\begin{array}{ccc}\cos 45^{\circ} & -\sin 45^{\circ} & 1 \\ \sin 45^{\circ} & \cos 45^{\circ} & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y \\ 1\end{array}\right] T(1,0)⋅R45 xy1 = 100010101 cos45∘sin45∘0−sin45∘cos45∘0001 xy1 = cos45∘sin45∘0−sin45∘cos45∘0101 xy1
-
矩阵有结合律 => 可以用 3x3 的矩阵表示很复杂的变换
-
矩阵可以分解的好处:
逆变换
变回来,相当于乘以一个矩阵的逆矩阵
旋转
已知旋转 θ \theta θ 角为:
- R θ = ( cos θ − sin θ sin θ cos θ ) R_\theta=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right) Rθ=(cosθsinθ−sinθcosθ)
那么,旋转 − θ -\theta −θ 角
- R − θ = ( cos θ sin θ − sin θ cos θ ) = R θ T R_{-\theta}=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right)=R_\theta^{\mathrm{T}} R−θ=(cosθ−sinθsinθcosθ)=RθT(数值上相同)
而根据定义,旋转 − θ -\theta −θ 角是旋转 θ \theta θ 角的逆变换:
-
R − θ = R θ − 1 R_{-\theta}=R_\theta^{\mathrm{-1}} R−θ=Rθ−1
-
正交矩阵:逆矩阵=转置矩阵
三维变换
-
用齐次坐标表示:
- 三维的点: ( x , y , z , 1 ) T \left(\mathbf{x}, \mathbf{y}, \mathbf{z}, \textcolor{red}{1}\right)^{\mathrm{T}} (x,y,z,1)T
- 三维的向量: ( x , y , z , 0 ) T \left(\mathbf{x}, \mathbf{y}, \mathbf{z},\textcolor{red}{0}\right)^{\mathrm{T}} (x,y,z,0)T - 向量具有平移不变性
-
( x , y , z , w ) (x, y, z, w) (x,y,z,w) 在 w ≠ 0 w\neq 0 w=0 时表示一个三维空间中的点,即 ( x w , y w , z w ) (\frac{\mathrm{x}}{ \mathrm{w}}, \frac{\mathrm{y}}{\mathrm{w}}, \frac{\mathrm{z}}{\mathrm{w}}) (wx,wy,wz)
-
用 4 × 4 4\times4 4×4的齐次坐标来表示仿射变换
- ( x ′ y ′ z ′ 1 ) = ( a b c t x d e f t y g h i t z 0 0 0 1 ) ⋅ ( x y z 1 ) \left(\begin{array}{l}x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1\end{array}\right)=\left(\begin{array}{llll}a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1\end{array}\right) \cdot\left(\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right) x′y′z′1 = adg0beh0cfi0txtytz1 ⋅ xyz1
- 先应用线性变换,再加上平移
缩放
- S ( s x , s y , s z ) = ( s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ) S(s_x, s_y, s_z) =\left(\begin{array}{llll}s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1\end{array}\right) S(sx,sy,sz)= sx0000sy0000sz00001
平移
- T ( t x , t y , t z ) = ( 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ) T(t_x, t_y, t_z)=\left(\begin{array}{llll}1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1\end{array}\right) T(tx,ty,tz)= 100001000010txtytz1
旋转
齐次坐标
-
绕着 x 轴, y轴, z轴旋转
-
绕着 x 轴旋转 R x ( α ) = ( 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ) R_x(\alpha)=\left(\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right) Rx(α)= 10000cosαsinα00−sinαcosα00001
-
绕着 y 轴旋转 R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) R_y(\alpha)=\left(\begin{array}{llll}\cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right) Ry(α)= cosα0−sinα00100sinα0cosα00001
-
绕着 z 轴旋转 R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) R_z(\alpha)=\left(\begin{array}{llll}\cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right) Rz(α)= cosαsinα00−sinαcosα0000100001
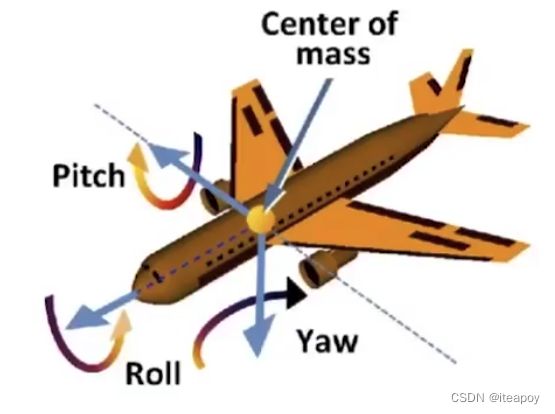
欧拉角
-
三维旋转
- R x y z ( α , β , γ ) = R x ( α ) R y ( β ) R z ( γ ) \mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_x(\alpha) \mathbf{R}_y(\beta) \mathbf{R}_z(\gamma) Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)
-
- roll
- pitch
- yaw
-
Rodirgues 旋转公式
- 绕着旋转轴 n n n (默认是过原点的轴)旋转 α \alpha α 角都可以变成 绕着 x, y, z 旋转
- R ( n , α ) = cos ( α ) I + ( 1 − cos ( α ) ) n n T + sin ( α ) ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^T+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0\end{array}\right)}_{\mathbf{N}} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)N 0nz−ny−nz0nxny−nx0
- ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N \underbrace{\left(\begin{array}{ccc}0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0\end{array}\right)}_{\mathbf{N}} N 0nz−ny−nz0nxny−nx0 表示叉乘
-
四元数
观测变换(viewing)
view/camera transformation 视图变换
- 从三维变成二维的图片
-
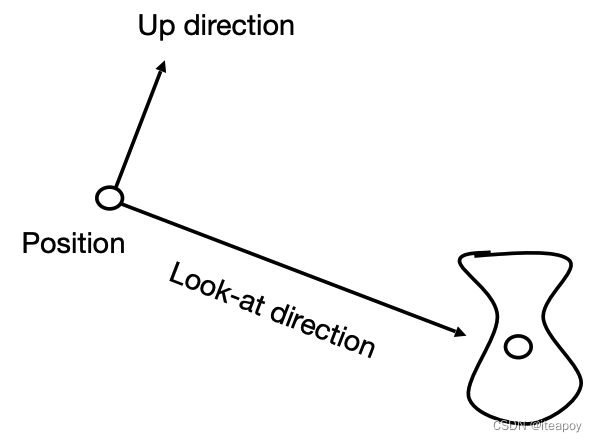
定义一个相机:
- 位置 e ⃗ \vec{e} e
- 看的方向(look-at) g ^ \hat{g} g^
- 向上的位置 t ^ \hat{t} t^ (假设是垂直于 look-at 的位置)
-
因为物体和相机是相对的,假设相机的位置固定
-
如何进行视图变换?
- 将相机的位置 e ⃗ \vec{e} e 平移到原点 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)
- 把 g ^ \hat{g} g^ 转到 − Z -Z −Z 方向
- 把 t ^ \hat{t} t^ 转到 Y Y Y 方向
- 把 g ^ × t ^ \hat{g}\times\hat{t} g^×t^ 转到 X X X 方向
projection transformation 投影变换
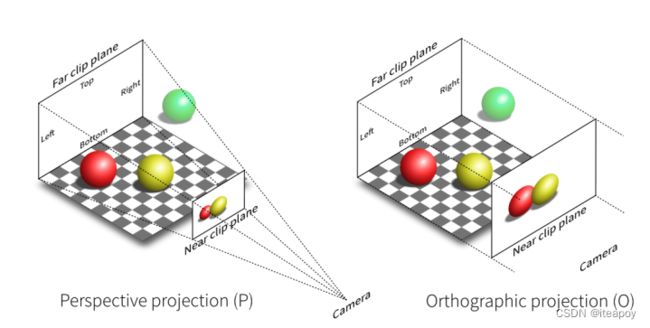
- 正交投影 vs. 透视投影
- 正交投影:不会造成近大远小的视觉差
- 正交投影:认为相机是一个点
- 透视投影:认为相机是无限远
Orthographic projection 正交投影
-
如何把一个 [ l , r ] × [ b , t ] × [ f , n ] [\mathbf{l}, \mathrm{r}] \times[\mathrm{b}, \mathrm{t}] \times[\mathbf{f}, \mathbf{n}] [l,r]×[b,t]×[f,n] ( n > f n>f n>f)的物体变到相机坐标系中?
- **相机固定在原点 ( 0 , 0 , 0 ) (0,0,0) (0,0,0),往 − Z -Z −Z 方向看,向上是 Y Y Y
- 把z轴丢掉,就都在一个平面上啦!
- 再把 xy 平面的图归一化到 [ − 1 , 1 ] [-1,1] [−1,1]
-
沿着 − Z -Z −Z 方向看
- 离人近 Z Z Z 值大
- 离人远 Z Z Z 值小
-
正交投影变换矩阵:先平移到原点,再旋转变换(注意后一个式子中最后一列和平移矩阵最后一列的缩放关系)
- M ortho = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] M_{\text {ortho }}=\left[\begin{array}{cccc}\frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1\end{array}\right]\left[\begin{array}{cccc}1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1\end{array}\right] = \left[\begin{array}{cccc}\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1\end{array}\right] Mortho = r−l20000t−b20000n−f200001 100001000010−2r+l−2t+b−2n+f1 = r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1
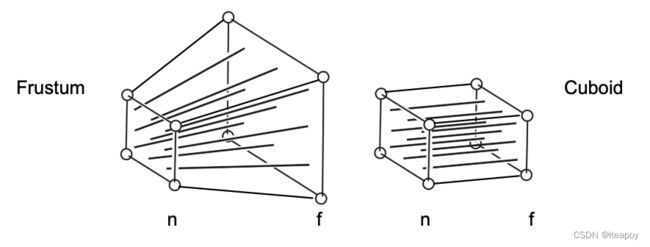
perspective projection 透视投影
-
怎么做?
- 先把远平面挤压成和近平面一样大小( M persp → ortho M_{\text {persp } \rightarrow \text { ortho }} Mpersp → ortho )
- 再进行正交投影( M ortho M_{\text {ortho }} Mortho )
-
公式: M persp = M ortho M persp → ortho M_{\text {persp }}=M_{\text {ortho }} M_{\text {persp } \rightarrow \text { ortho }} Mpersp =Mortho Mpersp → ortho
- M persp → ortho = ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0\end{array}\right) Mpersp → ortho = n0000n0000n+f100−nf0
3 光栅化
-
定义屏幕:一个数组
-
raster (德语)屏幕
-
光栅化:把图画到平面上
-
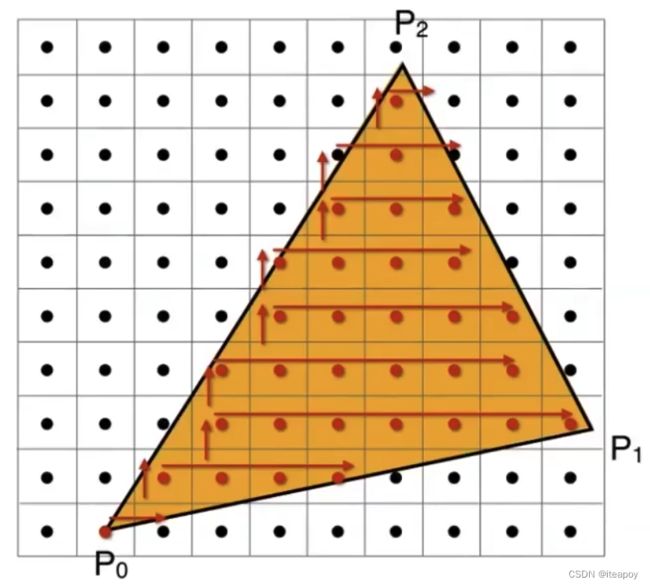
用三角形来表示物体
-
光栅化的优化
-
在绿色上有更多的感光元件(人眼对绿色更敏感)
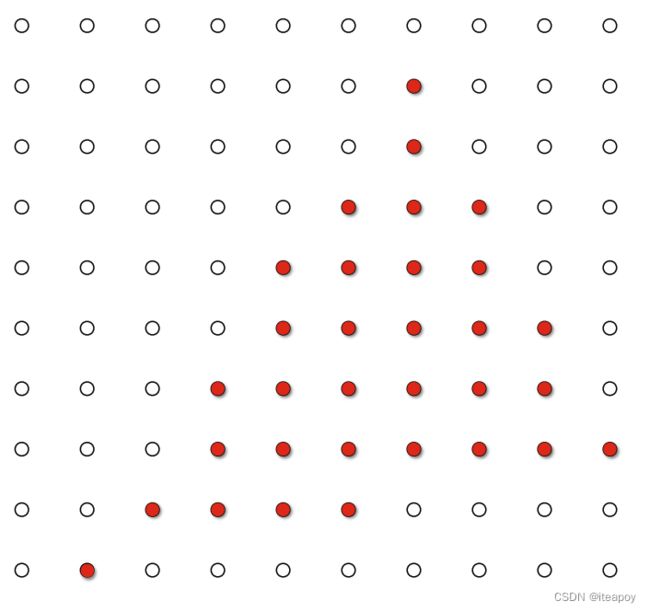
锯齿问题
-
采样导致的问题:
- 锯齿(空间中的采样)
- 摩尔纹(空间中的采样,删除偶数行和偶数列)
- 车轮倒转(时间中的采样)
-
原因:
- 信号变化太快
- 采样太慢,跟不上变化的速度
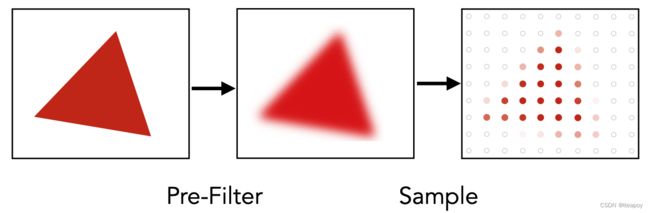
抗锯齿
-
又名:反走样 antialiasing
-
如何减少走样误差:
-
vs. 超分辨率
- 低分辨率到高分辨率
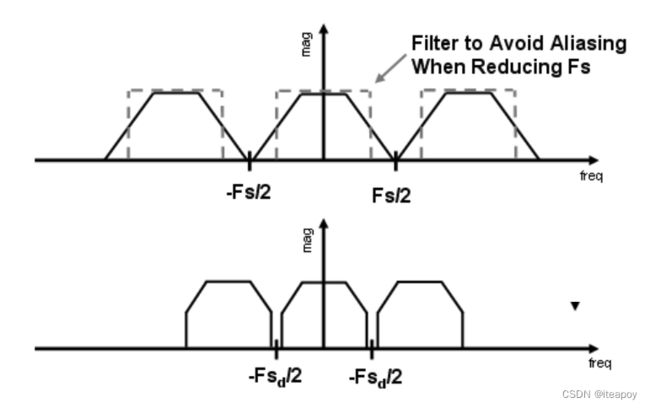
滤波
-
滤波
- 删除某段频率后,对应的信号如何变化
-
傅立叶变换
- 把时域变成频域
-
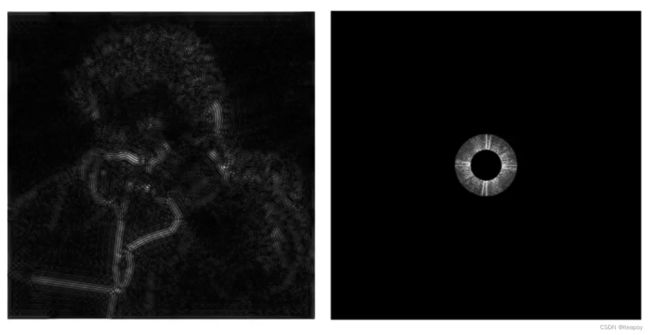
高通滤波(high-pass filter)
-
只有高频信号可以通过,只剩下高频信息,丢掉低频信息
-
只剩下边界
-
-
低通滤波(low-pass filter)
-
过滤掉最高频和最低频
-
滤波 (= 平均)= 卷积
- 时域的卷积 = 频域的乘积
- 选择1:
- 时域上做卷积
- 选择2:
- 转换到频域(傅立叶变换)
- 乘上卷积的傅立叶变换
- 转换回时域(逆傅立叶变换)
深度测试 Z-buffer
-
解决的问题:
- 可见性 / 遮挡
-
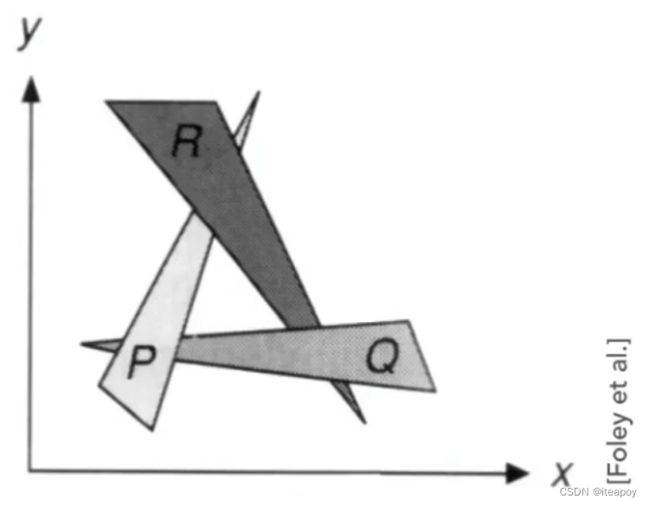
画家算法
-
Z-buffer
- !!! 重要:假设离我们近的z更大,离我们远的z更小
- 对每个像素,记录 min(z-value) 的深度
- 需要两个buffer
- frame buffer:存颜色
- depth buffer:存深度
- 时间复杂度: O ( n ) O(n) O(n)(n个三角形)
- 一个问题:
- 对于msaa来说,z-buffer不一定是对像素点,而是对采样点
-
处理不了透明物体的深度