（十）Java算法：归并排序（详细图解）

一、前言

1.1、概念

   归并排序：是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

1.2、算法原理

  我们大概讲一下算法的原理。

1. 申请一个和原数组同样大小的空间，降低空间复杂度
2. 将一个要排序的序列从中间位置（$\frac{left+right}{2}$）分成左右两个子序列
3. 在将这两个子序列按照第一步继续二分下去，直到所有子序列的长度都为1，也就是不可以再二分截止，（比如8个数的序列分成两个只含4个数的序列，4个数的序列再分成两个只含2个数的序列，两个数的序列最后分成两个只含1个数的序列）
4. 两两合并成一个有序序列（比如两个只含1个数的序列合成一个2个数的序列，两个只含2个数的序列合成一个4个数的序列，两个只含4个数的序列合成一个8个数的序列）
5. 这样通过分治法完成排序

二、maven依赖

pom.xml

<dependencies>
    <dependency>
        <groupId>org.springframework.bootgroupId>
        <artifactId>spring-boot-starterartifactId>
        <version>2.6.0version>
    dependency>

    <dependency>
        <groupId>org.projectlombokgroupId>
        <artifactId>lombokartifactId>
        <version>1.16.14version>
    dependency>
dependencies>

三、流程解析

  假设我们要排序的数据是：28, 19, 8, 23, 21,10, 9

3.1、整体流程图

  通过我们的整体流程图，来看看数据是怎么分，又是怎么合成的。

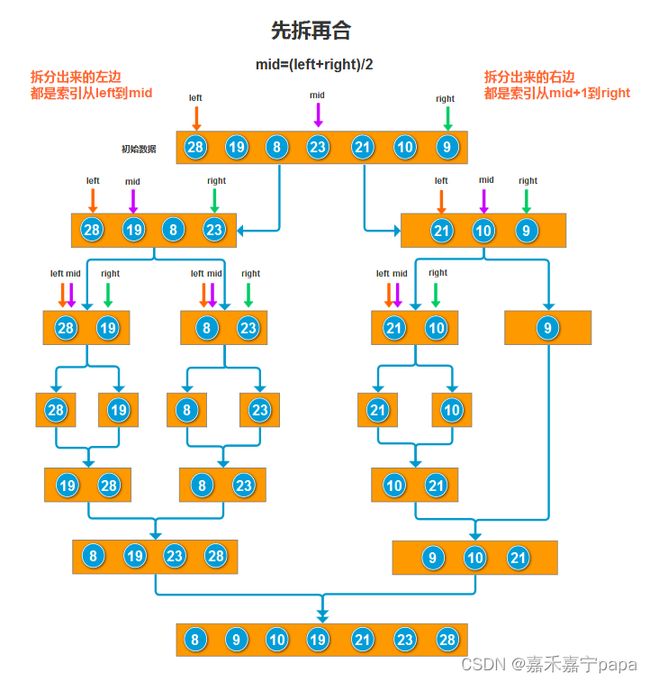
  就像我们之前说的，把一个数列分成两段，然后继续分，直到最后序列变成长度为1的序列；然后进行合并，两两合并为一个小序列，直到全部合成完成，就是一个递归的过程。

3.2、合并流程图

  上面我们演示了分和合的流程，但是可能对于合，可能大家还不是很理解，我们就吧最后两个数列合成的过程也演示下。

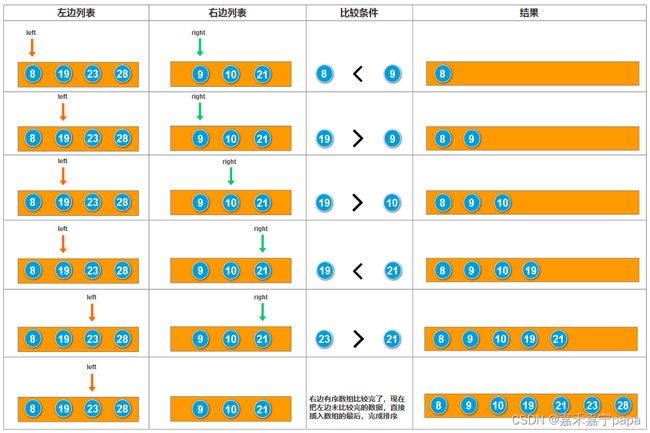
  也就是有两个数组的游标，都是从有序数列的左边开始，然后判断哪个值较小，就把取出较小的数放入到新的数组中，同时把它的游标继续往右移动，一直遍历，直到有一个数组已经比较完了，最后如果有数组未比较完成，则把未比较完的数据，放入到新数组的最后面。

四、编码实现

  假设我们要排序的数据是：28, 19, 8, 23, 21,10, 9

/**
 * 归并排序
 *
 * @param arr
 * @param left
 * @param right
 */
public static void mergeSort(int[] arr, int[] result, int left, int right) {
    if (left >= right) {
        return;
    }
    int mid = (left + right) / 2;
    mergeSort(arr, result, left, mid);
    mergeSort(arr, result, mid + 1, right);
    merge(arr, result, left, mid, right);
}

public static void merge(int[] arr, int[] result, int left, int mid, int right) {
    log.info("左边索引:【{}】,中间索引：【{}】,右边索引：【{}】", left, mid, right);
    int k = left;
    int l = left;
    int r = mid + 1;
    while (l <= mid && r <= right) {
        result[k++] = arr[l] < arr[r] ? arr[l++] : arr[r++];
    }
    // 左边数组还有未比较的直接加入到临时数组
    while (l <= mid) {
        result[k++] = arr[l++];
    }
    // 右边数组还有未比较的直接加入到临时数组
    while (r <= right) {
        result[k++] = arr[r++];
    }
    // 临时数组未已排序的拷贝到原数组
    for (int i = 0; i < result.length; i++) {
        arr[i] = result[i];
    }
    log.info("【{}】和【{}】合并结果：{}", left, right, arr);
}

public static void main(String[] args) {
    int[] arr = new int[]{28, 19, 8, 23, 21, 10, 9};
    int[] result = Arrays.copyOf(arr, arr.length);
    log.info("要排序的初始化数据：{}", arr);
    //从小到大排序
    mergeSort(arr, result, 0, arr.length - 1);
    log.info("最后排序后的结果：{}", arr);
}

运行结果：

要排序的初始化数据：[28, 19, 8, 23, 21, 10, 9]
左边索引:【0】,中间索引：【0】,右边索引：【1】
【0】和【1】合并结果：[19, 28, 8, 23, 21, 10, 9]
左边索引:【2】,中间索引：【2】,右边索引：【3】
【2】和【3】合并结果：[19, 28, 8, 23, 21, 10, 9]
左边索引:【0】,中间索引：【1】,右边索引：【3】
【0】和【3】合并结果：[8, 19, 23, 28, 21, 10, 9]
左边索引:【4】,中间索引：【4】,右边索引：【5】
【4】和【5】合并结果：[8, 19, 23, 28, 10, 21, 9]
左边索引:【4】,中间索引：【5】,右边索引：【6】
【4】和【6】合并结果：[8, 19, 23, 28, 9, 10, 21]
左边索引:【0】,中间索引：【3】,右边索引：【6】
【0】和【6】合并结果：[8, 9, 10, 19, 21, 23, 28]
最后排序后的结果：[8, 9, 10, 19, 21, 23, 28]