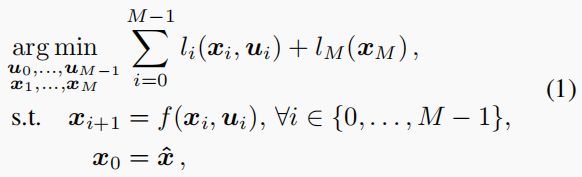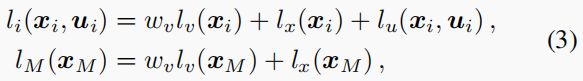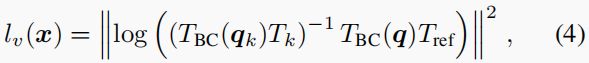论文笔记（三十七）Visually Guided Model Predictive Robot Control via 6D Object Pose Localization and Tracking

文章概括

作者：Mederic Fourmy♣ Vojtech Priban♣ Jan Kristof Behrens♣ Nicolas Mansard♢ Josef Sivic♣ Vladimir Petrik♣
来源：arXiv:2311.05344v1 [cs.RO] 9 Nov 2023
原文：https://arxiv.org/abs/2311.05344
代码、数据和视频：
系列文章目录：
上一篇：
https://blog.csdn.net/xzs1210652636/article/details/134431873
下一篇：

摘要

这项工作的目的是利用安装在机器人上的摄像头，完成与动态运动物体的 6D 姿态相关的操纵任务。例如，保持机器人手臂相对于物体的恒定 6D 姿态、抓取动态运动物体或与人类共同操纵物体。在这种情况下，快速准确的 6D 姿态估计对于实现平滑稳定的机器人控制至关重要。这项工作有三个方面的贡献。首先，我们提出了一种新的视觉感知模块，它异步结合了基于学习的精确 6D 物体姿态定位器和基于高速率模型的 6D 姿态跟踪器。其结果是从输入视频流中以高达 120 Hz 的频率进行低延迟、准确且时间上一致的 6D 物体姿态估计。其次，我们开发了一种视觉引导机械臂控制器，它将新的视觉感知模块与基于扭矩的模型预测控制算法相结合。将视觉信号和机器人本体感觉信号以相应频率进行异步组合，可实现稳定、鲁棒的 6D 物体姿态引导机械臂控制。第三，我们在一个具有挑战性的 6D 姿态估计基准上对所提出的方法进行了实验验证，并在一个真实的 7 DoF Franka Emika Panda 机器人上演示了动态移动物体的 6D 物体姿态引导控制。

1. 介绍

从移动机器人的路径跟踪 [1] 到视觉伺服 [2]，视觉引导控制是许多机器人应用的核心。为了实现稳定、鲁棒的反馈回路，感知系统必须准确、高速地恢复估计状态。在物体操纵方面，通常选择的状态表示是感兴趣物体的 6D 姿态，即场景中物体相对于摄像机坐标系的三维平移和三维旋转。虽然有些操纵任务可以通过静态场景模型来实现 [3]，但许多应用本身就具有动态性质，例如人机交接 [4]、[5]、人机协同操纵 [6] 或移动操纵 [7]。这就要求对场景中的目标物体进行精确、低延迟的 6D 姿态估计，因此具有挑战性。此外，姿势估计还需要与能够满足应用动态要求的鲁棒性反应控制器相结合。

尽管最近在物体检测和 6D 姿态估计方面取得了令人鼓舞的进展 [8]、[9]、[10]、[11]、[12]、[13]，但 6D 物体姿态估计算法通常注重精度而非速度。另一方面，6D 物体姿态跟踪方法能快速更新已检测到的物体姿态，但需要用户进行初始化 [14]。由于这些限制，现实世界中的许多应用都依赖于靶标[15]、[16]、[17]、运动捕捉系统[6]、[5]或基于颜色分割的临时检测[18]。

在本文中，我们提出了一种视觉感知模块，该模块基于（i）最先进的基于精确学习的 6D 物体姿态检测器和（ii）最先进的基于高速率模型的 6D 姿态跟踪器，以实现仅受图像采集速率限制的物体姿态估计。此外，我们还开发了基于模型预测控制（MPC）的视觉引导机器人控制器，该控制器能够反应性地将感知更新纳入其中，以满足应用目标（如定位机器人的抓手）。MPC 的预测特性使其特别适合实时生成高效运动 [19]。原则上，所需的唯一输入数据就是用于配置 6D 姿态跟踪器和 6D 姿态估计器的 3D 物体模型。我们的方法在独立进程中运行姿态检测器和多个物体跟踪器实例，并使用姿态检测器的结果重新初始化跟踪器。新图像会直接馈送至跟踪器，因此在跟踪器运行时间约为 5 毫秒的情况下就能获得姿态估计结果。为了定量验证我们的感知模块，我们在 BOP 挑战评估[9]和 YCBV 数据集[20]的基础上，测量了建议方法和几种基线方法的性能。最后，我们用手持物体演示了视觉引导的机器人手臂控制（见图 1）。

图 1： 通过物体的 6D 姿态控制机械臂。目的是通过指令关节扭矩来控制安装了摄像头（红色箭头）的机械臂，从而使物体的 6D 姿态（蓝色箭头）相对于摄像头保持不变。机器人摄像头捕捉到的三个帧（见插图）与主图中绿色等值线所示的机器人/物体姿势相对应，说明了这一点。请注意（见插图），在捕捉到的帧中，当背景发生变化时，物体的姿态如何保持稳定。更多结果和实验分析请参阅配套视频。

贡献。 本文有以下三个主要贡献：

• (i) 我们提出了一种新的视觉感知模块，该模块异步结合了基于学习的精确 6D 物体姿态定位器和基于模型的高速 6D 姿态跟踪器；
• (ii) 我们开发了一种视觉引导机械臂控制器，该控制器在基于扭矩的模型预测控制算法中利用了新的视觉感知模块；
• (iii) 我们在一个具有挑战性的 6D 姿态估计基准上对所提出的方法进行了实验验证，并在一个真实的 7 DoF Franka Emika Panda 机器人平台上演示了动态移动物体的 6D 物体姿态引导控制。

我们将公开代码。

2. 相关工作

物体 6D 定位。 近年来，物体检测和 6D 姿态估计领域取得了令人瞩目的进展，6D 物体姿态估计基准（BOP）和相关的 BOP 挑战[8]、[9]记录并促进了这一进展。大多数方法都采用两步法，首先在 RGB 帧[21]中进行物体检测，然后假设有物体网格，进行 6D 姿态估计。基于学习的技术在该领域占据主导地位。在各种方法中，渲染-比较法[22]、[10]、[13]通过根据神经网络的预测迭代改进 6D 姿态，取得了卓越的性能。由于其迭代性质，这些方法虽然性能优越，但在实时控制中使用时速度较慢。在这项工作中，我们建议将缓慢的 "渲染和比较 "6D 姿态定位器与快速的 6D 姿态跟踪器结合起来。虽然我们提出的方法可以使用任意定位器，但我们在所有实验中都使用了预训练的 CosyPose [10]。

物体 6D 姿态跟踪。 如果对物体的 6D 姿态有一个良好的初始猜测，就可以通过快速的局部方法进行逐帧跟踪。物体姿态跟踪方法依赖于物体边缘 [23]、提取的点特征 [24]、[25] 或深度 [26]。基于区域的跟踪方法建议通过构建图像后验分布来联合解决二维物体形状分割和六维姿态跟踪问题[27]。虽然最初的版本需要高度优化的 GPU 实现才能以相机频率运行 [28], [29]，但基于轮廓点采样的稀疏公式 [30] 大幅缩短了计算时间，在单个 CPU 上每幅图像的计算时间仅为几毫秒 [31], [14]。在这项工作中，我们依靠的是 ICG 实现[14]，它同时具有基于区域和深度的模式。我们在本文中提出的 6D 姿态定位器和本地 6D 姿态跟踪器的组合结合了两者的优点，即定位器的检测能力和准确性以及跟踪器的速度。

视觉伺服。 视觉伺服的目的是利用摄像机流中的视觉信息建立一个闭环控制器，以实现特定目标。各种方法传统上分为两大类[2]：(i) 基于图像的视觉舵机[32]、[33]，它使用二维几何基元（如点、曲线）来定义图像空间中的控制目标；(ii) 基于姿态的视觉舵机[34]、[35]，它假定目标六维姿态的估计值可用。一些研究建议根据运动阶段在基于图像和姿态的伺服系统之间进行切换 [36]。虽然基于图像的伺服可以自然地将可见性约束纳入控制法则，但基于姿态的伺服更接近于物体抓取等应用[5]。我们要解决的难题是，如何为基于姿态的控制获得鲁棒且快速的 6D 姿态估计值。这些研究通常在关节速度层面实施控制法则，缺乏基于转矩控制的自然阻抗。

视觉伺服的模型预测控制。 对于基于图像的视觉伺服，MPC 已显示出优于传统反应式控制器的性能 [37]，[38]。图像空间中的系统动态可通过分析方法近似计算 [37], [38] 或通过基于学习的光流估计方法计算 [39]。基于图像的 MPC 伺服被成功应用于控制无人机 [40]、脚踏平台 [18] 或移动机械手 [41]、[42]。与使用图像空间 MPC 的先进方法不同，我们建议使用 MPC 进行基于姿态的控制，其中 6D 姿态由拟议的感知模块获得。

3. 物体姿态引导模型预测控制

拟议系统的目标是利用安装在机器人上的摄像头，根据动态运动物体的 6D 姿态执行操纵任务。在这种情况下，我们的方法所要解决的主要技术难题在于实现精确的 6D 姿态估计，同时不给控制环路带来明显的延迟。然后将估计的 6D 姿态与 MPC 结合使用，实现对机器人的最优控制。

所提出的方法是一种 1 kHz 扭矩级 MPC 控制器，以从 30 Hz 图像流中获得的 6D 物体姿态为参考。为实现这种实时机器人控制性能，感知和控制模块异步运行，如图 2 所示。

感知模块检测场景中感兴趣的物体，并以快速和时间上一致的方式对其进行跟踪，如第 III-A 节所述。创新的关键在于通过时延校正器模块处理精确但缓慢的 6D 姿态定位器和快速但本地的跟踪器之间固有的不同步性，该模块对缓冲图像进行操作，以便及时跟上。感知模块检测到的 6D 物体姿态将被最优控制问题（OCP）[43] 求解器和反馈控制器使用，反馈控制器使用里卡提增益线性化求解[44]，以 1 kHz 的频率计算机器人的扭矩，详见第 III-B 节。在下面的章节中，I 符号代表 RGB 图像帧，T∈SE(3) 是刚体变换。

图 2：感知-控制循环概述。反馈控制的目标是跟踪摄像头所见物体的 6D 姿势，如右图中的机器人和红色芝士盒。为实现这一目标，我们设计了一个感知（Perception）模块，该模块在输入图像 $I_k$ 上运行一个快速局部跟踪器（fast local $Tracker$），其初始姿态 $T_{k-1}$ 可从跟踪器的上一次运行中选择，也可从$6DPoseLocalizer$和$TimeDelayCorrector$模块中选择（如果有相关信息的话）。$6DPoseLocalizer$的运算速度较慢，而$TimeDelayCorrector$的目标是在$6DPoseLocalizer$计算时，通过快速跟踪缓冲区中存储的图像来及时追赶。$Tracker$的输出，即姿态 $T_k$，被$OCPSolver$用于计算里卡提增益 $K_0$ 和力矩 ${\tau }_0$，这些被$RicattiLinearization$模块用于为实时机器人控制提供快速反馈。单个模块的典型处理频率为：6D 姿态定位器和时延校正器为 5 Hz，摄像头和跟踪器为 30 Hz，OCP 求解器为 100 Hz，机器人实时控制为 1 kHz。

A. 时间一致的 6D 物体姿态跟踪器

感知模块的目标是根据在离散时间 k 观察到的输入图像 $I_k$，计算场景中物体的 6D 姿态，同时尽可能减少延迟。尽管所提出的方法可以跟踪任意数量的物体，但为了简化符号，我们只描述单个物体姿态 $T_k$ 的跟踪。

6D 姿态定位器（6D Pose Localizer）。 在计算资源不受限制的情况下，物体的姿态可通过 6D 姿态定位器 估算，该定位器可检测图像中的相关物体，并估算其相对于摄像机坐标系的 6D 姿态，因此也可估算机器人坐标系的 6D 姿态，因为我们假设摄像机相对于机器人进行了校准。然而，稳健的物体定位器速度较慢，例如在最新的硬件上，CosyPose [10] 为 0.25 秒，MegaPose [13] 甚至为 30 秒（见第四部分）。漫长的计算时间使得定位器无法用于闭环控制。

跟踪器（Tracker）。 为了缓解这一限制，我们将定位器与快速本地跟踪器相结合，后者可根据给定图像 $I_k$ 和初始姿态猜测 $T_{k-1}$ 计算物体的姿态。与定位器相比，跟踪器的单次通过速度很快，只给系统带来几毫秒的延迟。但是，它只能在局部发挥作用，因此需要根据观察到的图像完善初始姿态。跟踪器无法发现新物体的存在，也无法检测到摄像机不再能看到的物体，例如，当物体被遮挡时。

物体定位与跟踪 (OLT)。 我们将定位器和跟踪器合并为一个感知模块 ，以 $f_{track}$ 的频率计算快速反馈，同时并行运行 $f_{localize}$，以进行物体（再）发现和更精确的姿势估计。我们的架构如图 2 的感知板所示，在当前图像上运行 ，其初始姿态 $T_{init}$ 可从以下两种情况中选择：(i) 跟踪器的上一次迭代，即 $T_{k-1}$；或 (ii) 如果Time Delay Corrector已计算出上一幅图像 $I_{k-1}$ 的信息，即图像缓冲区（Buffer）的末端，则可通过单独的进程定位物体。当进入系统的第一帧图像经过定位器和时延校正器处理后，主跟踪器即被初始化。

时间延迟校正器（Time Delay Corrector）。 在并行过程中，本地化器的单个实例在资源可用的情况下一直运行。假设定位器在时间 $k-N$ 开始处理输入图像 $I_{k-N}$，需要一段时间才能获得 $f_{localize}$ 的输出，在此期间会有新的图像到达并堆叠在缓冲区内。一旦计算出姿态 $T_{k-N}=f_{localize}(I_{k-N})$，跟踪器的第二个实例就会在缓冲区内的所有图像上运行，即 $T_i=f_{track}(I_i,T_{i-1})$ 对 $i\in \{k-N+1,...,k-1\}$，同时向主跟踪器进程提供在 $k-1$ 时刻计算出的最终姿态。感知模块的时间轴如图 3 所示。请注意，我们的架构假设 $f_{track}(.)$ 的频率高于输入图像流的频率。否则，定位器进程将永远追不上主进程。使用最先进的跟踪器 [14]，可以很容易地计算出图像频率高达 120 Hz 的反馈。然而，输入图像频率越高，从定位器进程注入信息所需的时间就越长。这将影响跟踪精度，我们将在第四部分进行分析。

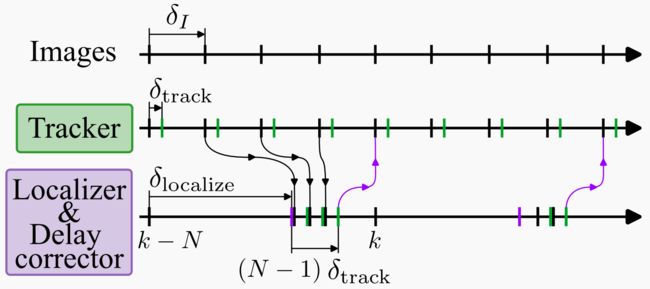
图 3：感知模块时间轴。 第一行显示的是图像流，图像之间的典型延迟${\delta }_I$ 为 33 毫秒。第二行显示的是跟踪器模块（即 $f_{track}$）造成的延迟，用 ${\delta }_{track}$ 表示，相当于几毫秒，因此输出姿势（绿色刻度线）是以输入图像流的频率产生的。如紫色箭头所示，跟踪器需要初始姿态，初始姿态可能来自跟踪器的上一次运行，也可能来自 6D 姿态定位器和时延校正器模块。6D 姿态定位器运行 $f_{localize}$（${\delta }_{localize}$ 通常为几百毫秒），然后在缓冲图像上应用 $N-1$ 次 $f_{track}$（第三行中的绿色刻度线）。

B. 使用 MPC 进行基于姿势的 6D 视觉伺服

我们设计了一种控制器，可将连接在机器人末端执行器上的摄像头与从物体跟踪器中获得的物体姿态 $T_k$ 保持用户定义的相对姿态。在实际应用中，我们可以从一组预定义的抓取姿势中为给定物体选择一个参考姿势。控制的难点在于机器人需要以 1 kHz 的频率实时接收扭矩指令。为了应对这一挑战，我们在 [44] 的基础上，将控制分为以 100 Hz 频率求解最优控制问题和通过里卡提线性化计算 1 kHz 反馈，但在问题表述中加入了 6D 物体姿势作为指导参考。

OCP 求解器。 控制模块的主要目标是根据感知器提供的最新物体姿态估计值 $T_k$ 和当前机器人状态 $x=(q^{\top }{\dot{q}}^{\top }{)}^{\top }$（$q$ 和 $\dot{q}$ 分别为测量到的关节角度和速度）来跟踪物体。我们对机械手进行力矩控制（即 $u=\tau$），以利用机械手的自然动态，获得更平滑的运动。通过解决最优控制问题（Optimal Control Problem: OCP），可以在固定的时间范围内获得最佳状态和控制轨迹，其中最优性由一组加权高层次目标定义。OCP 的解析是在微分动态编程（DDP）[45] 的框架内进行的，并使用可行性驱动 DDP 求解器[43]来实现。通过使用直接多次射击策略将连续问题离散化，将 OCP 转换为非线性程序：

其中，$\hat{x}$ 是最新的机器人状态测量值，$x_i$ 和 $u_i$ 是离散时间 $i$ 时的机器人状态和应用控制，$f(x_i,u_i)$ 描述了机器人动力学（即铰接体算法），$l_i$ 和 $l_M$ 分别是运行成本和终端成本。控制的跟踪目标由成本指定，我们将在第 III-C 节中介绍。给定初始猜测后，DDP 算法会求解 (1)，并通过贝尔曼递推迭代返回一系列状态和控制动作（详见 [43]）。

里卡提线性化。 除了琐碎的系统和较短的时间跨度外，OCP 不可能在机器人控制频率（即 1 kHz）下求解。不过 [44] 研究表明，作为 OCP 解法的副产品，里卡提增益 $K_0$ 可用来实现最优策略的一阶近似值。用 ${\tau }_0=u_0^{\ast }$ 表示 OCP 求解器得到的最优控制的第一步，最优策略的线性近似值为：

其中，$x$ 是最新的机器人状态测量值，$x_0$ 是找到 OCP 解决方案的机器人状态。这种计算是即时的，它将 OCP 问题的复杂性与实时性约束分离开来，并允许我们解决长视距问题。

C. 跟踪目标

控制器的行为由公式 (1) 中的运行成本和终端成本定义。对于我们的跟踪问题，我们将成本表述如下：

其中，$l_v(.)$ 是按 $w_v$ 缩放的跟踪成本，$l_x(.)$ 和 $l_u(.)$ 分别是状态正则化成本和控制正则化成本。

跟踪成本。 我们定义的跟踪成本是最小化估计物体姿态与参考物体姿态 $T_{ref}$ 之间的 SE(3) 距离，两者均以机器人基帧表示，即：

其中，$T_k=f_{OLT}(I_k)$ 是建议的跟踪器估算出的物体姿态，$T_{BC}(.)$ 代表从机器人基座到摄像机的前向运动学，运算器对数代表 SE(3) 对数图[46]。如果机器人摄像头和估计物体姿态之间的变换接近 $T_{ref}$，则跟踪成本趋近于零。

状态正则化成本。 我们将状态正则化成本定义为 $l_x(x)=(x-x_{rest}{)}^{\top }{Q}_x(x-x_{rest})$，其中 $x_{rest}=(q_{rest}^{\top }{0}^{\top }{)}^{\top }$ 惩罚远离固定静止构型 $q_{rest}$ 的关节构型，同时惩罚高关节速度。正则化成本的目的是防止机器人的无效空间（null-space）运动，即不影响摄像机本身姿态的运动。这对冗余机器人来说是必需的，因为在这种情况下，机器人的多工位数高于任务空间的多工位数。对关节速度进行规范化可以防止求解器计算出过于激进的运动。我们将 $q_{rest}$ 设置为启动控制器后读取的第一个配置。

控制正则化成本。 控制正则化是通过 $l_u(x,u)=(u-u_{rest}(x){)}^{\top }{Q}_u(u-u_{rest}(x))$ 来实现的，正则化控制使其不偏离 urest(x)，其中 urest(x) 是补偿机器人配置 x 重力的力矩。

4. 实验

在本节中，我们首先在 YCBV 数据集[20]上对所提出的感知模块进行定量评估，该数据集包含标准化对象，我们在本节的第二部分中也将其用于在真实的弗兰卡-艾米卡熊猫机器人上进行 6D 姿态引导反馈控制任务。对于定位器的实现，除非另有说明，我们使用 CosyPose [10]，对于跟踪器，我们使用 ICG [14]。

A. 感知模块的定量评估

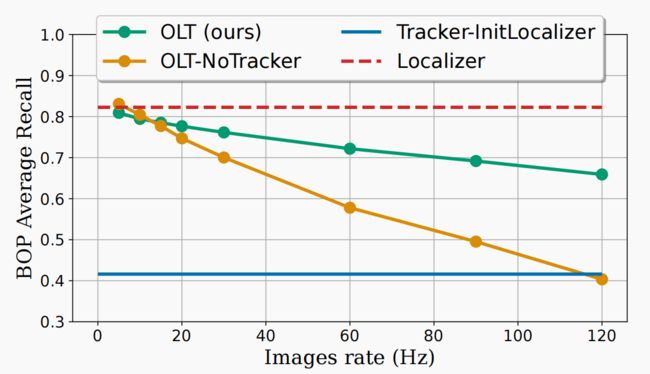
我们使用 6D 物体姿态（BOP 基准）评估指标[9]，对 YCBV 数据集[20]上的新感知模块进行了定量评估。YCBV 数据集由多个移动摄像头视频组成，展示了数据集中 22 个可用对象的子集。视频的每一帧都标注了场景中所有可见物体的真实姿态。我们之所以使用 YCBV 数据集，是因为该数据集提供了用于真实世界实验的真实物体，以及用于 CosyPose [10] 物体姿态估计器的预训练模型。我们使用 BOP 工具包 [9] 计算标准 6D 姿态误差指标，以评估姿态估计的质量。评估程序将输入视频序列中的图像按顺序和给定频率输入感知模块。通过评估 [9] 中定义的 BOP 平均召回分数，将输出姿势与地面实况进行比较。评估程序的结果如图 4 所示，接下来将进行讨论。

图 4：BOP 指标[9]的平均召回率（越高越好），用于衡量不同物体定位和跟踪实现的 6D 姿态估计的准确性。比较在同一硬件上以不同频率重放的 YCBV 视频数据集上进行。

评估基线。 图中显示了两条主要基线：(i) Localizer，在视频的每一帧上运行定位器；(ii) Tracker-InitLocalizer，在视频的第一帧上运行由定位器计算初始化的跟踪器。两条基线均以水平线显示，因为它们是根据图像流的频率独立评估的。定位器在系统中引入了较高的时间延迟，因此不适合闭环控制。不过，结果表明定位器是准确的。另一方面，跟踪器在线运行时延迟很小，但无法（重新）发现新的或丢失的目标轨迹。因此，其平均召回率较低。

OLT 评估。 我们的方法（OLT）介于两条基线之间。它的在线运行延迟与跟踪器相同，但在低频输入图像流中也能达到定位器的召回率。随着定位器输出姿态注入跟踪器的频率降低，平均召回率随频率增加而下降。渐进地，当图像流频率接近跟踪器的计算频率时，OLT 的召回率将接近纯跟踪器的性能，因为时延校正器将永远无法及时赶上跟踪器进程。

无跟踪器的 OLT。 为了评估跟踪器的影响，我们进行了一项消融研究，将跟踪器重新定义为身份映射，即 $T_k=f_{track}(I_k,T_{k_1}):=T_{k-1}$。图 4 显示了不同图像流频率下的召回率，即 OLT-NoTracker 曲线。可以看出，与身份跟踪器相比，ICG 跟踪器（即 OLT（我们的））的影响随着频率的增加而增大。因此，本地跟踪器在定位器的计算时间内发挥了重要作用。需要注意的是，这种影响对于快速移动的物体更为明显，而 YCBV 数据集中并不存在快速移动的物体。

结果的可复制性。 如图 4 所示，我们方法的平均召回率取决于输入图像流的频率，因为定位器生成更准确的 6D 姿态的频率较低。因此，计算值也取决于硬件，因此只有在可比设置上运行时才具有可比性。我们在同一台配备 12 核 AMD® Ryzen Threadripper PRO 3945WX CPU 和 NVIDIA GeForce RTX 3080 GPU 的电脑上对所有方法进行了评估。

B. 视觉引导反馈控制

我们使用以下实验装置对 6D 物体感知模块的设计和 MPC 控制器进行了实验验证。我们使用一个 7 DoF 的 Franka Emika Panda 机器人，在其末端执行器上安装了一个 RealSense D455 摄像头（手眼配置）。摄像头与末端执行器的安装位置已校准。我们将摄像头配置为以 30 Hz 的频率生成分辨率为 640x480 的 RGB 视频流。我们以扭矩级控制模式控制熊猫机器人，该模式要求以 1 kHz 频率发送指令。这就需要使用 Ricatti Linearization 模块，该模块可确保以这一频率计算扭矩指令。OCP 由 Crocoddyl [43] 解决，它使用了 Pinocchio [47] 的高效机器人动力学实现。为了建立机器人的动力学模型，我们使用了 [48] 中的惯性参数。感知模块的计算和 OCP 解算由第 IV-A 章所述的计算机处理。1 kHz 里卡提线性化控制环在另一台实时计算机上计算，以保证熊猫机器人的响应时间要求。实时计算机与非实时计算机之间的通信使用机器人操作系统（ROS）[49]实现。

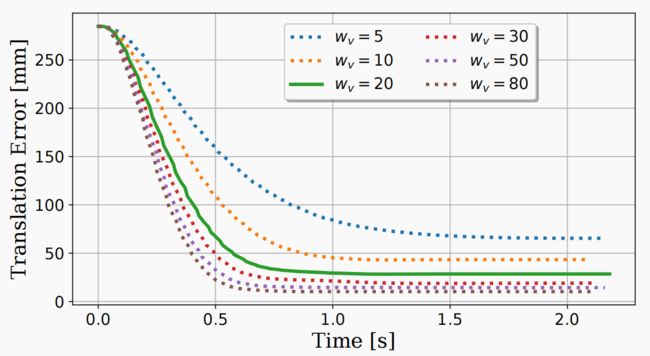
MPC 控制评估。 为了评估 MPC 控制的质量，我们在熊猫机器人上进行了一项实验，分析了人为将目标 6D 姿态旋转 30 度后控制器的阶跃响应，即本实验中未使用感知模块。图 5 显示了不同跟踪权重 wv 值下平移跟踪误差的变化情况（见公式 (3)）。结果证实，跟踪器趋近目标，稳态误差取决于跟踪权重。方向误差（未显示）也遵循相同的模式。根据结果，我们选择跟踪权重 $w_v$ 等于 20，因为对于我们的任务来说，稳态误差是可以接受的，而且较低的权重会降低控制器的攻击性。成本中的其他权重设置为 $Q_x=diag(0.3,...,0.3,3,...,3)和Q_u=diag(0.1,...,0.1)$。

图 5：MPC 的阶跃响应（无感知） 模拟目标姿态旋转 30 度后的步进响应。

MPC 跟踪验证。 我们建立了一个闭环机器人控制实验，如图 6 所示，在该实验中，感知和控制模块使我们能够将机器人的末端执行器带到一个与 YCBV 物体相关的所需参考姿态。尽管末端执行器的运动速度相对较快，而且物体表面存在镜面反射，但跟踪器仍能在整个运动轨迹中保持对物体姿态的准确估计。更多示例请参见附带视频。

图 6：阶跃响应实验的可视化。第一行显示的是安装在机器人上的摄像头拍摄的图像，以及我们的感知模块估算的姿势投影（绿色等高线）和目标参考姿势投影（蓝色等高线）。第二行显示的是外部摄像头捕捉到的机器人运动图像。控制器的目标是将机器人末端执行器移动到与检测到的物体姿态相对应的固定相对姿态。机械手的初始配置有意设置为远离目标，以评估系统的阶跃响应。控制器会在 1.5 秒内将摄像头拉近到所需的参考姿态。有关其他示例和实验分析，请参阅补充视频。

5. 结论

要实现机器人与动态移动物体的交互，例如在人机交接任务中，就必须进行精确且低延迟的物体姿态估计。我们的研究表明，高精度但速度较慢的 6D 姿态定位器与快速帧对帧 6D 姿态物体跟踪器相结合，可以获得低延迟（< 5 毫秒）的姿态估计。所提出的算法已通过以下两个方面得到验证：(i) 对常见家用物体基准的定量研究；(ii) 开发基于 MPC 的物体姿态跟踪反馈控制器。这项工作为三维动态环境中的视觉引导操纵提供了可能性，例如，在人机协作或移动机器人操纵中，无需靶标或运动捕捉系统。