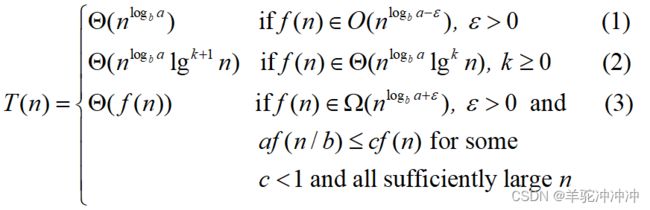算法设计与分析
目录
三个渐进记号
分治策略
①迭代法
②递归树法
③主定理法
分治的应用
堆
堆应用
动态规划
动态规划应用
贪心算法
贪心算法应用
回溯法
回溯法应用
图
图的遍历
BFS
DFS 记录时间戳
拓扑排序
强连通分量
最小生成树
流网络
NP、P
摊还分析
三个渐进记号
O(g(n)) = { f(n) : 存在正常量c和n0,使得对所有n ≥ n0,有0 ≤ f(n) ≤ cg(n)}
渐近下界记号 Ω
Ω(g(n)) = { f(n) :存在正常量 c 和 n0,使得对所有 n³ n0 有 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
渐近紧确界记号Θ
Θ(g(n)) = { f(n) : 存在正常量c1, c2和n0,使得对所有n ≥ n0,有0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n)}
分治策略
①迭代法
②递归树法
③主定理法
主方法可解如下形式的递归式
T(n) = aT(n/b) + f(n)
关键是看 f(n) 和 nlogba 谁比较大。
Case 1 成立,如果 nlogba 较大 ,那么T(n) = Θ(nlogba ).
Case 2 (当 k = 0) 成立,如果 f(n) 和 nlogba 大小相当。T(n) = Θ(f(n)lgn).
一般来说, 当 f(n) 和 nlogba lgkn 大小相当 ,T(n) = Θ(f(n) lgk+1n).
Case 3 成立,如果 f(n) is 较大 è T(n) = Θ(f(n)).
分治的应用
最大子数组
矩阵乘法Strassen
凸包问题
棋盘覆盖问题
二维最近点对问题
堆
堆应用
动态规划
动态规划主要用于求解以阶段划分的动态过程的优化问题。
最优子结构,用反证法证。问题的最优解是由其子问题的最优解来构造,则称该问题具有最 优子结构性质。
动态规划要定义符号,找关系,写出递推公式,记得写边界条件。
动态规划有最普通的递归,自顶向下带备忘的,自底向上打表的。
动态规划应用
贪心算法
贪心算法应用
回溯法
回溯法应用
图
图的遍历
BFS
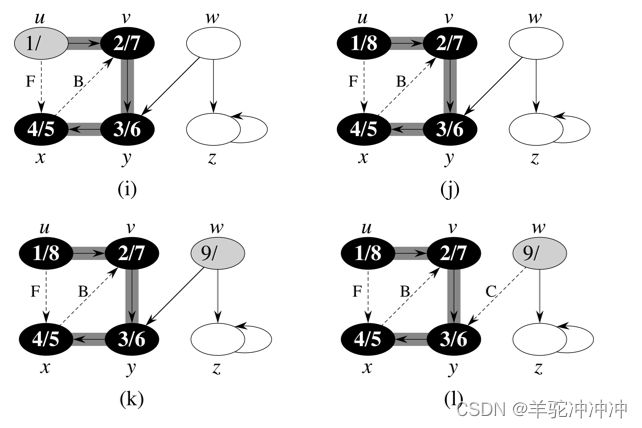
白色节点表示该节点还未被访问
灰色节点表示它被访问过,但是还没有对它的所有邻居进行访问
黑色节点表示它被访问过,而且已经访问了它的所有邻居
DFS 记录时间戳
拓扑排序
只有有向无环图才可以拓扑排序。
先选没有入度的点,删了它和它的边,再选没有入度的点。
强连通分量
先dfs一次,在转置图上,按照时间戳最大的开始dfs,几次dfs就是几个连通分量。
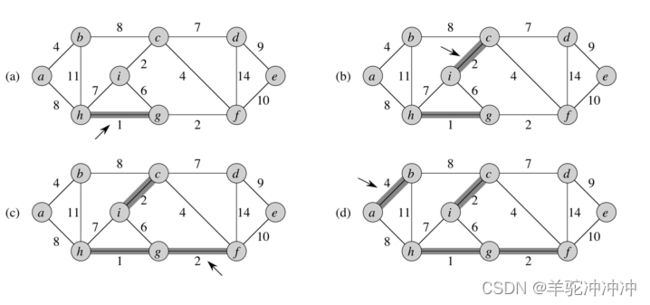
最小生成树
prim
Kruskal稀疏图比较好,Prim稠密图比较好。
Kruskal算法实现简单一点。
流网络
NP、P
①Q是NP问题
②任何NP问题都可以归约到Q
则称:Q为NPC问题。