第十五周周报

摘要

本周做数据挖掘和数据分析的大作业时，发现仅对评论进行积极和消极的态度的评价还不够，还得找到其与态度相关的关键字，比方说：坑、贵、海拔高、祖母朗玛峰；好、美、值得、纳木错；我们就可以大概知道，哪里景点负面情况多，哪些景点值得一去。
项目是用的在主流网站上爬取的近54000多条评论数据。经过数据清洗、数据预处理、数据分词等操作后，使用LDA模型进行分析，最后分成4个主题，每个主题具有不同关键词的概率组合，具有显著的相异性，从而完成对数据信息的挖掘。

This week, while working on a major project involving data mining and data analysis, I discovered that evaluating comments solely based on positive and negative sentiments is not sufficient. It is essential to identify keywords associated with attitudes. For example, terms like “pitfall,” “expensive,” “high altitude,” and “Everest” may indicate a negative sentiment, while terms like “good,” “beautiful,” “worth it,” and “Nam Lake” may suggest a positive sentiment. By doing so, we can gain insights into which tourist attractions have more negative feedback and which ones are worth visiting.
The project involved crawling data from major websites, resulting in over 54,000 comments. After performing operations such as data cleaning, preprocessing, and segmentation, I utilized the LDA (Latent Dirichlet Allocation) model for analysis. The data was eventually categorized into four main topics, each characterized by a unique combination of keywords with different probability distributions. These topics exhibited significant dissimilarities, thereby successfully extracting valuable information from the data.

LDA模型（隐含狄利克雷分布（Latent Dirichlet Allocation））

目前对LDA模型的掌握和了解，只知道可以将文章扔进模型中，模型最后输出的各个主题及主题对应不同关键词的概率矩阵，和各篇文章对应不同主题的概率矩阵。生成一个词，首先是投掷文章对应不同主题的概率矩阵的“骰子”，然后得到的主题在投掷其对应不同关键词的概率矩阵的“骰子”；一直重复，生成一篇文章。再将这篇文章与投入的文章进行对比，不断优化其参数，使得最终稳定。

LDA模型的数学知识

Gamma函数
这个Gamma函数其实是为后面的Beta分布和Dirichlet分布做准备，具体它的数学之美我们就不在本文讨论，只需要记住以下的东西

Gamma函数定义：

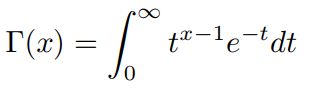通过分部积分的方法，可以推导出这个函数有如下的递归性质：

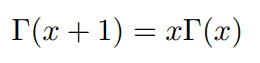
于是gamma函数可以当成是阶乘在实数集上的延展，具有如下性质：

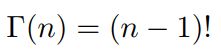
Beta分布：先存在一个概率分布情况，后面根据出现的情况，能够对其先验的概率分布进行改动的。可以看做一个概率的概率分布，当我们不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。


Beta分布是二项分布的共轭先验分布，Beta分布描述了二项分布中P取值的可能性，对于Betaf分布的随机变量，其均值可以估计为

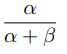
Beta-Binomial共轭
首先我们要记住贝叶斯参数估计的基本过程为：
先验分布+数据的知识=后验分布
更一般的，对于非负实数，我们有如下关系：

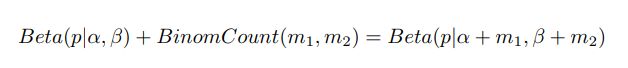
我们可以看到，参数的先验分布和后验分布都能够保持Beta分布的形式。

Dirichlet分布
狄利克雷分布是一组连续多变量概率分布，是多变量普遍化的Beta分布。

其中α是Dirichlet分布的参数。Dirichlet分布是多项式分布的共轭先验分布。

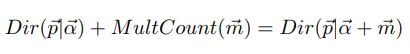
它的期望为

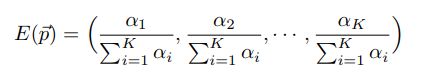
Dirichlet 分布是一个用于描述多维随机变量的概率分布。Dirichlet 分布的共轭性是指如果先验分布是一个 Dirichlet 分布，那么在观察到一些数据后，后验分布仍然是一个 Dirichlet 分布。这种性质在贝叶斯统计推断中非常有用，因为它简化了后验分布的计算。

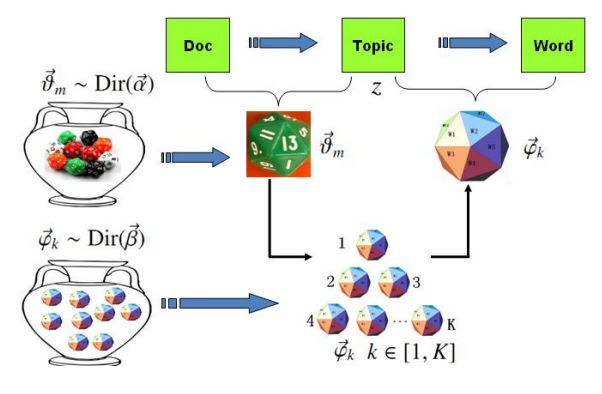
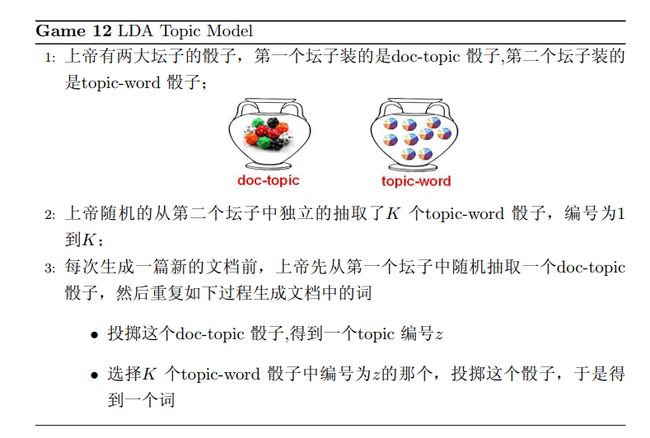
LDA假设文档主题的先验分布是DIrichlet分布，即对于任一文档d，其主题分布θd为：

其中，α为分布的超参数，是一个K维向量。
LDA假设主题中词的先验分布是DIrichlet分布，即对于任一主题k，其词分布βk为：

其中，η为分布的超参数，是一个V维向量，V代表词汇表里所有词的个数。
于数据中任一一篇文档d中的第n个词，我们可以从主题分布ηd中得到它的主题编号zdn
的分布为：

而对于该主题编号，得到我们看到的词
wdn的概率分布为：

理解LDA主题模型的主要任务就是理解上面的这个模型，这个模型，我们有M个文档主题的Dirichlet分布，而对应的数据有M个主题编号的多项分布，这样（α→θd→Zd）就组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。

如果在第d个文档中，第k个主题的词的个数为：n(k)d，则对应的多项分布的计数可以表示为：

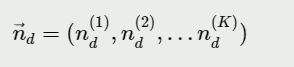
利用Dirichlet-multi共轭，得到θd的后验分布为：

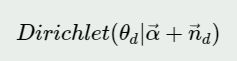
同样的道理，对于主题与词的分布，我们有
K个主题与词的Dirichlet的分布，而对应的数据有
K个主题编号的多项分布，这样(
η→βk→w(k)）就组成了组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。

如果在第k个主题中，第v个词的个数为：n(v)k
，则对应的多项分布的计数可以表示为：

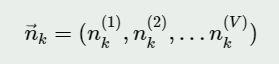
利用Dirichlet-multi共轭，得到βk。

是的，你的理解是正确的。在主题模型中，通常使用的是LDA（Latent Dirichlet Allocation）模型，其中涉及到主题-词分布和文档-主题分布。在LDA中，每个主题都与一个词的分布相关联，而每个文档都与一个主题的分布相关联。

具体来说，假设有K个主题，每个主题都由一个Dirichlet分布参数化，表示为β_k。每个主题k对应于一个多项分布，表示为多项分布参数η_k。这里，η是一个参数向量，可以与每个主题相关联。

文档d中的每个词都由文档的主题分布和主题的词分布生成。对于第k个主题中的第v个词，其生成的概率可以表示为：

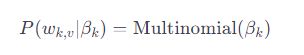其中，是由主题k的词分布β_k参数化的多项分布。
文档d的主题分布可以表示为Dirichlet分布：其中Dirichlet(a)是由参数α参数化的Dirichlet分布。
每个文档d中的词的生成概率可以表示为：

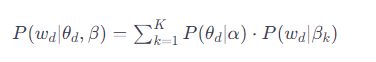
其中，θd是文档d的主题分布，而P(wd/βk)是主题k的词分布。
在贝叶斯推断中，通过观察文档中的词，可以计算后验分布，利用Dirichlet-Multinomial的共轭性质进行推断。这使得在LDA模型中使用贝叶斯方法更为方便。

LDA应用

在本周写的大作业中：利用LDA模型对其实现数据分析。在data里面，已经实现了积极和消极评论的分类。具体实现方法不在这里细讲。是通过分词和情感词及否定词的逻辑依次对各个评论进行处理的。

#建立词典、语料库
data=review_mltype.copy()
word_data_pos=data[data['ml_type']=='pos']
word_data_neg=data[data['ml_type']=='neg']

#建立词典，去重
pos_dict=corpora.Dictionary([ [i] for i in word_data_pos.word]) #shape=(n,1)
neg_dict=corpora.Dictionary([ [i] for i in word_data_neg.word])

#建立语料库
pos_corpus=[ pos_dict.doc2bow(j) for j in [ [i] for i in word_data_pos.word] ] #shape=(n,(2,1))
neg_corpus=[ neg_dict.doc2bow(j) for j in [ [i] for i in word_data_neg.word] ]

#构造主题数寻优函数
def cos(vector1,vector2):
    '''
    函数功能：余玄相似度函数
    '''
    dot_product=0.0
    normA=0.0
    normB=0.0
    for a,b in zip(vector1,vector2):
        dot_product +=a*b
        normA +=a**2
        normB +=b**2
    if normA==0.0 or normB==0.0:
        return None
    else:
        return ( dot_product/((normA*normB)**0.5) )


# 主题数寻优
# 这个函数可以重复调用，解决其他项目的问题

def LDA_k(x_corpus, x_dict):
    '''
    函数功能：
    '''
    # 初始化平均余玄相似度
    mean_similarity = []
    mean_similarity.append(1)

    # 循环生成主题并计算主题间相似度
    for i in np.arange(2, 11):
        lda = models.LdaModel(x_corpus, num_topics=i, id2word=x_dict)  # LDA模型训练

        for j in np.arange(i):
            term = lda.show_topics(num_words=50)

        # 提取各主题词
        top_word = []  # shape=(i,50)
        for k in np.arange(i):
            top_word.append([''.join(re.findall('"(.*)"', i)) for i in term[k][1].split('+')])  # 列出所有词

        # 构造词频向量
        word = sum(top_word, [])  # 列车所有词
        unique_word = set(word)  # 去重

        # 构造主题词列表，行表示主题号，列表示各主题词
        mat = []  # shape=(i,len(unique_word))
        for j in np.arange(i):
            top_w = top_word[j]
            mat.append(tuple([top_w.count(k) for k in unique_word]))  # 统计list中元素的频次，返回元组

        # 两两组合。方法一
        p = list(itertools.permutations(list(np.arange(i)), 2))  # 返回可迭代对象的所有数学全排列方式。
        y = len(p)  # y=i*(i-1)
        top_similarity = [0]
        for w in np.arange(y):
            vector1 = mat[p[w][0]]
            vector2 = mat[p[w][1]]
            top_similarity.append(cos(vector1, vector2))

        #        #两两组合，方法二
        #        for x in range(i-1):
        #            for y in range(x,i):

        # 计算平均余玄相似度
        mean_similarity.append(sum(top_similarity) / y)
    return mean_similarity

#计算主题平均余玄相似度
pos_k=LDA_k(pos_corpus,pos_dict)
neg_k=LDA_k(neg_corpus,neg_dict)

pd.Series(pos_k,index=range(1,11)).plot()
plt.title('正面评论LDA主题数寻优')
plt.show()

pd.Series(neg_k,index=range(1,11)).plot()
plt.title('负面评论LDA主题数寻优')
plt.show()

pos_lda=models.LdaModel(pos_corpus,num_topics=2,id2word=pos_dict)
neg_lda=models.LdaModel(neg_corpus,num_topics=2,id2word=neg_dict)

print(pos_lda.print_topics(num_topics=10))
print(neg_lda.print_topics(num_topics=10))

我对于pos里面的评论，设置了主题超参数为2，主题词为11。neg里面的负面评论，设置设置了主题超参数为2，主题词为11。

程序结果：

[(0, ‘0.038*“大峡谷” + 0.033*“美” + 0.020*“雅鲁藏布” + 0.015*“南迦巴瓦峰” + 0.014*“地方” + 0.013*“峡谷” + 0.012*“林芝” + 0.011*“雪山” + 0.011*“雅鲁藏布江” + 0.008*“中”’), (1, ‘0.021*“值得” + 0.017*“不错” + 0.016*“林海” + 0.015*“鲁朗” + 0.015*“景点” + 0.013*“高” + 0.012*“风景” + 0.009*“世界” + 0.007*“真的” + 0.006*“感觉”’)]
[(0, ‘0.028*“景点” + 0.021*“贵” + 0.018*“门票” + 0.012*“太” + 0.011*“地方” + 0.010*“差” + 0.009*“林海” + 0.009*“难” + 0.008*“走” + 0.007*“海拔”’), (1, ‘0.019*“高” + 0.015*“大峡谷” + 0.015*“低” + 0.011*“性价比” + 0.010*“坑” + 0.007*“雅鲁藏布江” + 0.006*“风景” + 0.006*“天气” + 0.006*“特别” + 0.005*“值得”’)]

总结

以上是我本周对LDA模型的理解和研究、及其在课程作业中的应用。目前对机器学习中数学方面的基础知识掌握不牢靠，在理解模型时感到相当吃力。