实用机器学习：线性回归的实际应用与解读

01 统计学基础

统计学的基本方法，在机器学习中的角色。

统计学是数据科学的基石，为机器学习提供了重要的理论和工具。它通过概率论、假设检验、回归分析等方法，帮助我们理解数据、进行推断和构建模型。以下是一些统计学概念的解释及应用：

解释	应用
概率论	概率论研究随机现象的数学理论。在机器学习中，概率论用于建模不确定性，例如通过概率分布描述数据的不确定性。用于分类、回归、聚类等算法中，通过概率模型进行预测和决策。
统计推断	统计推断涉及从样本中得出总体特征的过程。在机器学习中，统计推断可用于评估模型的性能、确定特征的重要性等。通过统计测试评估模型的显著性，进行参数估计，检验假设等。
回归分析	回归分析用于建立变量之间的关系模型。在机器学习中，线性回归、多项式回归等是常见的回归方法。用于预测数值型输出，如房价预测、销售预测等。
假设检验	假设检验用于评估关于总体参数的统计假设。在机器学习中，可以用于判断模型是否显著地优于随机猜测。在A/B测试中，判断两组数据是否存在显著差异。
贝叶斯统计学	贝叶斯统计学是一种基于贝叶斯定理的统计学方法，用于更新概率分布以反映新数据的方法。在贝叶斯机器学习中，用于处理不确定性、调整模型参数。
抽样理论	抽样理论研究如何从总体中选择样本，以便对总体进行推断。在机器学习中，样本的选择和处理对模型性能至关重要。保证样本的代表性，避免抽样偏差，提高模型的泛化能力。

02 先谈下回归和分类的不同

回归和分类是机器学习中两种不同类型的任务，它们分别处理不同的问题。

回归关注的是连续型输出变量的预测，而分类关注的是将输入数据分为不同的离散类别。有着不同的应用场景和目标。

任务类型	问题类型	例子	目标
回归	预测连续型输出变量	预测房价、股票价格、销售额等	找到一个模型，学习输入特征与连续型输出变量之间的关系，从而对新的输入进行预测。
分类	划分输入数据到不同离散类别	判断邮件是垃圾邮件还是非垃圾邮件、图像中的物体是猫还是狗等	训练一个模型，使其能够将输入特征映射到预定义的类别标签，并对新的输入进行分类。

以最简单的线性回归为开端，探讨机器学习的基本算法原理，同步通过动手操作，加深对原理的理解掌握及应用。

03 线性回归原理

线性回归是统计学习方法中的一种经典模型，属于监督学习的范畴。

线性回归通过建立线性关系的模型，描述自变量与因变量之间的关系。它是统计学习中的一种回归分析方法，用于预测连续型的因变量。

线性回归的基本思想是假设因变量（目标变量）与自变量之间存在线性关系，并通过最小化残差平方和（最小二乘法）来估计模型参数，找到一条最佳拟合的直线。线性回归模型的数学形式通常表示为：

其中：

y 是因变量（目标变量），

ω0 是截距（偏置），

ω₁,ω₂,…,ωn 是自变量 χ₁,χ₂,…,χn 的权重，

ε是误差项。

线性回归模型是参数化模型，通过学习训练数据来估计模型参数，使其能够对新的输入进行预测。在实际应用中，线性回归被广泛用于经济学、生物学、工程学等领域，为了解和预测变量之间的关系提供了有力的工具。

04 线性回归代码实现

使用Python和Scikit-Learn库演示线性回归的实现。

代码线性回归的实现过程，包括数据准备、特征工程、模型训练、预测和评估。

• 导入必要的库和数据：

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
from sklearn.preprocessing import StandardScaler

# 指定默认字体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 指定字体家族
plt.rcParams['font.family'] = 'SimHei'
# 解决保存图像是负号'-'显示未方块的问题
plt.rcParams['axes.unicode_minus'] = False

# 读取数据
path = './data/易速鲜花微信软文.csv'
data = pd.read_csv(path)

# 显示数据前几行
print(data.head())

打印结果如下，数据集有点赞数、转发数、热度指数、文章评级、浏览量共5列：

点赞数     转发数  热度指数  文章评级     浏览量0  2646  1347.0     7     5  2600041   816   816.0     4     6  1000042  1224   612.0     6     5  1645023 1261  1261.0    6     6  1630014 1720  1720.0    7     5  260401

• 清理数据并进行可视化操作：

# 数据清理，删除缺失值
data_clean = data.dropna()

# 可视化：散点图展示点赞数与浏览量的关系
plt.figure(figsize=(8, 6))
sns.scatterplot(x='点赞数', y='浏览量', data=data_clean, marker='o')
plt.xlabel('点赞数')
plt.ylabel('浏览量')
plt.title('点赞数与浏览量关系')
plt.show()

由上图可知，点赞数和浏览量有正相关关系，随着点赞数的增加，浏览量也有所增加。

• 进行特征工程：

# 特征选择
X = data_clean.iloc[:, :-1]
y = data_clean.iloc[:, -1]

# 特征相关性分析
plt.figure(figsize=(10, 8))
sns.heatmap(X.corr(), annot=True, cmap='coolwarm', fmt=".2f")
plt.title('特征相关性热图')
plt.show()

# 特征重要性分析
feature_importance = pd.Series(lin_model.coef_, index=X.columns)
feature_importance.plot(kind='barh', figsize=(10, 6))
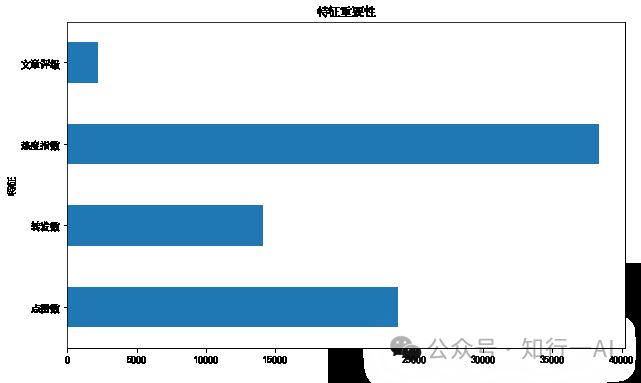
plt.title('特征重要性')
plt.xlabel('权重')
plt.ylabel('特征')
plt.show()

# 标准化特征
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

将点赞数、转发数、热度指数、文章评级作为特征变量，浏览量作为标签。

相关性热力图，x轴和y轴分别代表了不同的特征变量，每个格子的大小代表了两个变量之间线性相关程度的强度，红色表示两个变量正相关，蓝色表示负相关，灰色表示没有关系。

上图特征重要性分析，热度指数、点赞数、转发数对浏览量影响较大。

• 进行模型训练和预测：

# 数据拆分为训练集和测试集
X_train, X_test, y_train,
y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)

# 线性回归模型训练
lin_model = LinearRegression()
lin_model.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = lin_model.predict(X_test)

特征矩阵X包含了用于预测目标变量的所有特征，而目标变量矩阵y包含了每个样本的目标值（标签）。将数据集分为训练集和测试集是机器学习中常见的做法。训练集用于训练模型，而测试集用于评估模型的性能。

在训练过程中，本项目采用了线性模型，通过最小化均方误差的策略，指导通过算法（本项目梯度下降算法）逐步更新，这个策略指导了算法如何更新参数，以逐渐减小误差并提高模型的预测精度。训练完成后，lin_model将包含用于预测新数据的模型参数。（可以通过使用其他损失函数、及优化算法，以及交叉验证来调整优化模型）

• 评估模型性能：

# 输出模型权重和截距
print("当前模型的4个特征的权重分别是:", lin_model.coef_)
print("当前模型的截距（偏置）是:", lin_model.intercept_)

# 模型评估
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 输出模型评估指标
print('均方误差(MSE) is {:.2f}'.format(mse))
print('R^2分数是 {:.2f}'.format(r2))

打印结果：当前模型的4个特征的权重分别是: [23861.2891886 14127.26492673 38348.3715416 2193.15817207]

当前模型的截距（偏置）是: 181814.50667305756均方误差 (MSE) is 1502859487.48R^2分数是 0.80

R方（R Squared），也称为确定系数，用于衡量模型解释的变异占总变异的比例，越接近于1说明模型拟合越好。

• 真实值与预测值对比可视化：

# 可视化：真实值与预测值对比
data_compare = X_test.copy()
data_compare = pd.DataFrame(data_compare)
data_compare['真实值'] = y_test
data_compare['预测值'] = y_pred
plt.figure(figsize=(10, 6))
sns.lineplot(data=data_compare[['真实值', '预测值']], markers=True)
plt.title('真实值与预测值对比')
plt.show()

05 模型可解释性

模型解释性：

线性回归模型的解释性在机器学习中独具优势。每个特征的权重直观地展示了其对输出的影响程度，这使得我们能够深入了解模型对数据的理解。具体而言，权重为正的特征表明随着该特征的增加，输出也会相应增加，而负权重则表示增加该特征可能导致输出的减少。这直观的解释性质使得业务领域专业人士能够更容易理解和信任模型的预测结果。

可视化解释模型：

可视化工具在解释模型方面起到了关键的作用。通过残差图，我们可以直观地观察模型在预测中的误差分布，帮助识别模型可能存在的模式，有助于发现模型是否存在对某些观测值的系统性偏差。

# 残差分析：
residuals = y_test - y_pred
plt.figure(figsize=(10, 6))
sns.residplot(x=y_pred, y=residuals, lowess=True, color="g")
plt.title('残差分析')
plt.xlabel('预测值')
plt.ylabel('残差')
plt.show()

残差是实际值与模型预测值之差，如果模型拟合得很好，这些点应该大致沿着水平线分布，残差分析是评估模型拟合质量的重要步骤。

上文中特征重要性图则展示了各特征对输出的相对影响，为业务决策提供了直观的指导。这些可视化工具使非技术人员能够更容易理解模型的性能和输出。

06 结语

这个案例展示了线性回归在实际数据上的应用，通过训练模型并进行预测，我们可以评估模型的性能和拟合程度。线性回归易于理解，在某些简单情境下效果显著，但并不适用于所有问题。后续会陆续实现更复杂的模型和处理非线性关系的方法。

参考文献：

李航.统计学习方法.清华大学出版社

阅读原文：

实用机器学习：线性回归的实际应用与解读从0开始入门实用的机器学习算法之：线性回归https://mp.weixin.qq.com/s?__biz=MzkwNDYzNzkxNw==&mid=2247483759&idx=1&sn=c76a4f4b1806ee1871d9ac5d6fe206d3&chksm=c082bdddf7f534cb77f196f03297189f6522d598b940ce0b2164db00e65f70b8c314a62c6c04#rd

附数据集和代码JupyterNotebook地址：https://pan.baidu.com/s/1dkbUk_JADR4zL9egynublA

提取码：关注公众号（知行一AI，微信号：de2plearn），发消息“线性回归”自动获取