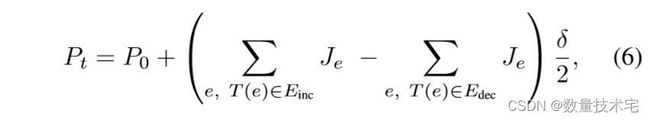基于霍克斯过程的限价订单簿模型下的深度强化学习做市策略

 

数量技术宅团队在CSDN学院推出了量化投资系列课程

欢迎有兴趣系统学习量化投资的同学，点击下方链接报名：

量化投资速成营（入门课程）

Python股票量化投资

Python期货量化投资

Python数字货币量化投资

C++语言CTP期货交易系统开发

数字货币JavaScript语言量化交易系统开发

---

相关研究总述

最优做市 (MM) 是在限价订单簿 (LOB) 的两侧同时下达买订单和卖订单的问题，目的是最大化交易者的最终收益率，同时最小化相关风险。 可以说，其中最突出的是库存风险，它源于交易者（做市商）在其库存中持有的标的资产的价格变动。 规避风险的做市商通常更愿意将其库存始终保持在接近于零的水平。 为了实现这一点，需要根据当前库存和其他相关变量不断调整下单（控制）价格。 这产生了 MM 作为随机最优控制问题的自然公式。 在最常用的框架内，首先在开创性的 Avellaneda-Stoikov (AS) 论文 [1] 中使用，后来被大量研究人员 [2]-[4] 研究和推广，问题归结为减少相关的 Hamilton- Jacobi-Bellman 方程转化为常微分方程 (ODE) 系统，并最终推导出最优 MM 控制的封闭形式近似。 或者，可以通过（深度）强化学习等技术获得接近最优的控制。

强化学习 (RL) 是一类用于在不确定条件下进行顺序决策的基于试错法的方法，用于解决构造为马尔可夫决策过程 (MDP) 的随机最优控制问题。 RL 方法在与深度神经网络（用作函数逼近器）结合时特别强大，合并到深度强化学习 (DRL) 的新领域。 近年来，从围棋游戏 [5] 到文本生成 [6] 和网络控制系统 [7] 等不同领域，DRL 取得了许多惊人的成就。 不出所料，如今人们对 (D)RL 在 MM 问题上的应用产生了浓厚的兴趣，MM 问题自然被定义为离散时间 MDP。

在 [8] 中，作者介绍了他们宣称是 RL 在高频交易中优化 MM 的第一个实际应用，使用 [9] 中提出的 LOB 模型通过简单的离散 Q-Learning 训练 RL 代理。 然后作者证明他们的框架优于 AS 和固定偏移量基准。 有点类似，Spooner 等人。 [10] 使用带有瓦片编码线性组合的 SARSA 算法作为价值函数逼近器来生成 RL 代理，该代理在多种证券中表现出卓越的样本外性能。 Sadighian [11] 开发了一个加密货币 MM 框架，该框架采用两种先进的基于策略梯度的 RL 算法（A2C 和 PPO）和一个由 LOB 数据和订单流到达统计信息组成的状态空间。 Gaˇsperov 和 Kostanjˇcar [12] 提出了一个以对抗性强化学习和神经进化的思想为基础的框架，实验结果证明了其优越的风险回报性能。 其他值得注意的方法引入了额外的功能，如暗池的存在 [13]、公司债券中的多资产 MM [14] 和交易商市场 [15]。

无论使用何种方法，原始的 LOB 建模，理想地考虑市场微观结构的经验属性和程式化事实以及 LOB 本身的离散性质，对于获得高性能 MM 控制器至关重要。 然而，由于它们所基于的天真假设，大多数当代 MM 方法的 LOB 模型在方向、时间和数量方面仍然不一致，导致回测和荒谬事件下的虚假收益 [16]，比如价格在之后下跌 一个大的买入市场订单。 举个例子，在最初的 AS 模型 [1] 中，假设价格变动完全独立于市场订单的到达和 LOB 动态，而随后的方法仅部分解决了这种不一致。 为了改善这一点，[16] 中提出了一种新颖的弱一致性纯跳跃市场模型，该模型可确保价格动态与 LOB 动态在方向和时间方面保持一致。 尽管如此，它仍然假设订单到达强度恒定，这意味着各种类型的 LOB 订单到达之间的任何（经验发现的）自我或相互激励和抑制的影响仍然无法解释。

在本文中，我们考虑了做市商在弱一致性、基于多变量霍克斯过程的 LOB 模型中进行交易的随机最优控制问题。 据作者所知，我们的方法是第一个在这种模型下将 DRL 与 MM 结合起来的方法。 一方面，我们的目标是增加现有 MM 模型的真实性，例如 [16] 中提出的模型。 鉴于霍克斯过程通常用于市场微观结构的现实建模 [17]-[19]，我们选择这样的模型，然后将其用作我们模拟器的支柱。 另一方面，我们还需要确保不危及易处理性。 为此，我们避免使用完整的 LOB 模型（因为相关的复杂性和问题 [16]），而是选择简化形式的 LOB 模型。 此外，还做出了一些关于微观结构动力学的额外简化假设。 因此，我们工作的基础是仔细考虑复杂性和易处理性之间的平衡。从做市商的控制（选择限价和市价订单）影响订单到达强度，即市场响应的意义上讲，该模型也是交互式的 动态地对做市商的控制策略。 所提出的方法有助于（在我们看来）弱一致 LOB 模型下 MM 研究的代表性不足 [16]。 它还可以利用蒙特卡罗回测的优势，特别是它执行受控随机实验的能力 [20]。

准备工作

多元霍克斯过程

p 维线性霍克斯过程 [21] 是一个 p 维点过程 N(t) = (Nk(t) : k = 1,...,p)，Nk（第 k 维）的强度由下式给出 :

​

其中 µk ≥ 0 是基线强度，Nl(t) 对应于第 l 个维度的 [0,t] 内的到达数，fk,l(t) 内核（触发函数）。 对于 t > s，维度 l 的到达扰动维度 k 在时间 t 到达的强度 fk,l(t−s)。 多元线性霍克斯过程相对容易处理，并且由于其分支结构表示 [22]，因此很适合模拟和解释。 在使用指数内核的情况下，强度由下式给出：

​

其中 βk,l ≥ 0 和 αk,l ≥ 0 是衰减和激发参数。

模型

事件类型

我们采用 Biais [23] 提出的 LOB 事件分类，包括 12 种不同类型的 LOB 事件，如下图所示。为简单起见，不考虑非典型订单，例如冰山订单或（部分）隐藏订单 . 激进的市价单、限价单和取消（类型 1-6 的事件）会影响买入价或卖出价，因此也会影响中间价。 非激进市价订单（类型 7-8）不影响任何价格； 但是，它们会产生交易并影响 LOB 顶部的交易量，因此与 MM 相关。 非激进限价订单和取消（类型 9-12）既不影响 LOB 顶部的价格也不影响交易量，因此被忽略。 因此，我们总共考虑了 8 种事件类型：

​

​

其中上标表示（非）攻击性，下标表示一侧（买/卖）。 生成的 LOB 模型在 [16] 之后是弱一致的。 允许可变跳跃大小，LOB 动态由 8 变量标记点过程建模，其中标记表示跳跃大小。 对应的计数过程为：

​

以及相关的强度向量：

​

在用 Je 表示与单个事件 e 关联的跳跃大小（以滴答为单位）后，中间价格 Pt 由下式给出：

​

其中 P0 是初始价格，δ 是报单量大小，T(e) 是事件 e 的类型，Einc = {Ma b ,La b,Ca s}，Edec = {Ma s ,La s,Ca b}。 为了简单起见，假设跳跃大小与跳跃时间独立同分布且无关。 （与 [16] 中的类似）。

仿真过程

具有指数内核的多元线性霍克斯过程用于对不同 LOB 顺序到达（即事件类型）之间的依赖性（即交叉激励和自激励效应）进行建模。 选择指数内核的动机是它们易于模拟，并且适用于对描述市场微观结构的短期记忆过程进行建模，因此它们传统上用于金融应用程序 [24] [25]。 此外，它们的使用方便地导致过程的马尔可夫特性 [17] [26]。 为了模拟多元霍克斯过程，我们依赖 Ogata 的改进细化算法 [27]。

做市程序

MM 过程大致遵循 [1] 中描述的过程。 在每个时间步的开始，在时间 t，代理（控制器）取消其未完成的限价订单（如果有的话），并观察包含市场和基于代理的特征的环境状态 St。 代理使用此信息来选择操作 At - 它决定是发布限价订单（以及以什么价格）或市场订单。 如果代理人库存的绝对值等于库存约束c，c∈N，则忽略对应方的订单。 所有相关的市场（中间价、买价和卖价、价差）和基于代理的（库存、现金）变量都会相应更新。 接下来，依次处理模拟程序生成的 LOB 事件，然后对相关变量进行相应的更新。 在下一个时间步长开始之前，已执行的限价单不能被新的替代。 最后，智能体到达时间步的末尾并收到奖励 Rt+Δt。 当到达时间 t + Δt 时，上一时间步未执行的限价订单被取消，智能体观察环境的新状态 St + Δt，选择动作 At + Δt 并迭代该过程直到终止时间 T . agent's inventory 由以下关系描述：

​

其中 Nb t 、 Na t 、 Nmb t 和 Nms t 分别表示到时间 t 为止执行的代理的限价买单、限价卖单、市价买单和市价卖单的数量。 Nb t 过程描述为：

​

其中 1fill, Ma s (1fill, Mn s ) 是传入（非）激进市价订单是否满足做市商限价订单的指标函数。 过程 Na t 类似地描述。 最后，代理程序的现金处理 Xt 由下式给出：

​

其中 Qa t (Qb t) 表示发布做市商的要价（出价）报价，Pa t (Pb t ) 为最佳要价（出价），t 表示所有在时间 t由于费用和市场影响而产生的额外成本。 此外，还做出了一些简化假设：

做市商提交的市价订单激进的概率为 Z1，其限价订单取消的激进概率为 Z2。

密度由 f(x) = 1 /β * exp (−(x−µ)/β) 给出的指数分布用于模拟与激进事件相关的价格跳跃 Je 的大小，其中 µ 是位置，β 是尺度参数。 在需要的情况下（即具有激进的限价订单和取消），使用具有相应参数的截断指数分布。

在非激进市价单到达后，以最佳买入/卖出价执行做市商限价单的概率由 Z3 确定并给出。 限价订单要么全部执行，要么根本不执行。

强化学习控制器

状态空间

状态空间由当前库存It、当前买卖差价Δt、趋势变量αt组成：

​

由于库存限制，有 2c + 1 种可能的库存状态，即 It ∈ {−c,...,c}。 当前的 bidask 价差 Δt 以刻度为单位测量并且严格为正。 变量 αt 说明了趋势并计算为 αt = λMa b (t) + λMn b (t)−λMa s (t)−λMn s (t)。 库存特征通过最小-最大归一化来归一化。 由于特征 Δt 和 αt 具有未知的均值和方差，我们通过控制器生成一个具有 100,000 步的长轨迹，该控制器输出完全随机的动作，并将获得的均值和方差用于 z-score 归一化。

动作空间

在时间 t 的操作（即控制）对应于最佳买入（卖出）价格的一对偏移量。 因此：

​

允许代理人以所有可能的价格发布限价订单，从而确定 LOB 每一侧的激进/保守水平。 如果代理发布一个带有负报价差价的限价订单对，则该操作将被忽略。 在最佳卖价（买价）或以上（以下）发布的买（卖）单被视为买（卖）市价单并立即执行。 假设做市商发送的所有限价单和市价单都具有单位大小（即针对资产的一个单位），并且控件四舍五入为报价大小的倍数。

奖励函数

MM代理的目标是最大化终端财富的期望，同时最小化库存风险。 我们从 [4] 中描述的常用 MM 公式中汲取灵感，并假设做市商最大化以下表达式：

​

在 RL 策略集上。 每个策略 π : S → P(A) 将状态映射到动作空间上的概率分布。Wt = It*Pt + Xt 是时间 t 的总财富，T 是终端时间，φ ≥ 0 是运行库存惩罚参数，用于阻止做市商持有非零头寸，从而使自己面临库存风险。 请注意，与 [4] 不同，我们使用库存的绝对值而不是二次库存惩罚来获得方便的风险价值 (VaR) 解释。 因此，时间 t + Δt 的奖励由下式给出：

被积函数是分段常数，因此是可以忽略的。

控制器设计

具有 64 个神经元的 2 个完全连接的隐藏层和 ReLU 激活的神经网络用于表示控制器。 这种相对较浅的架构在某种程度上是 DRL 中的标准，而且，之前已经证明简单的 NN 架构在 LOB 建模方面的性能与（或优于）复杂的 CNN-LSTM 架构相当[28]。

训练

SAC（Soft Actor-Critic）用于在我们的实验中训练 RL 控制器。 SAC 是一种最先进的 RL 算法，能够处理连续的动作空间，其特点是鲁棒性更高，并且能够学习多种接近最优行为的模式。 它是一种最大熵算法，这意味着它不仅使回报最大化，而且使策略熵最大化，从而改进探索。 或者，可以使用 DQN； 然而，我们的实验表明它存在严重的不稳定问题，尤其是在其原版版本中。 TD3（Twin Delayed DDPG）也曾被考虑过，但最终由于性能较差而被排除在外。 训练时间步数设置为 10的6次方。

实验

为了将我们的 DRL 方法的性能与 MM 基准进行对比，我们使用模拟器生成的合成数据执行蒙特卡罗模拟（回测）。 模拟次数设置为 10的3次方。像 AS [1] 近似这样的标准 MM 基准不适合我们的框架，因为它们既没有考虑 bid ask 传播的存在，也没有考虑基础 LOB [29] 的离散性质。 因此，我们需要转向替代基准。 我们考虑一类库存线性的 MM 策略，包括库存限制。 在这个类别的成员中，我们将表现最好的一个称为 LIN 策略。 请注意，此类策略还包括最先进的 Gueant-Lehalle-Fernandez-Tapia (GLFT) [3] 近似。 此外，我们考虑一个简单的策略（SYM 策略），它始终准确地以最佳出价和最佳要价放置限价单。

风险和绩效指标

每个策略都通过许多风险/绩效指标进行评估，尤其包括以下内容：

损益 (PnL) 分布统计、平均单次回报、平均绝对仓位 (MAP)、夏普比率、(MeanPnL)/MAP- 平均终末财富 (PnL) 与 MAP 的比值

实验结果

详细结果（PnL 和终端库存分布的分布统计以及所有策略的附加风险指标）在上表中提供。策略的终端 PnL 和库存分布以及高斯核密度如下图所示估计。

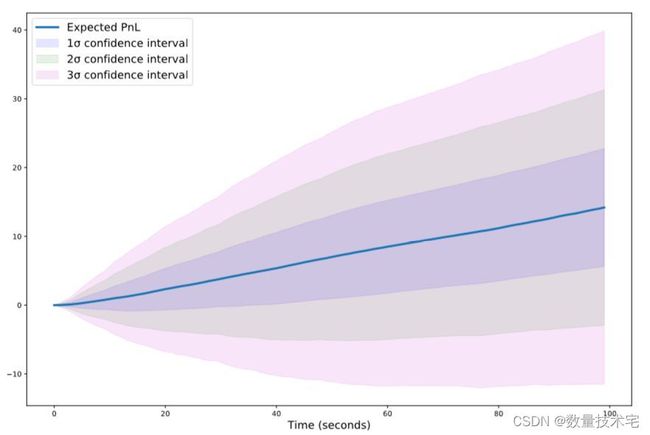
结果清楚地表明，就绝大多数考虑的指标而言，DRL 策略优于两个基准。 当与 SYM 和 LIN 策略并列时，DRL 策略性能结果显示出相当高的平均 PnL 值以及更有利的夏普比率。 PnL 分布（也解释为 VaR）的百分位数也表明其主要表现。 正如预期的那样，由于库存惩罚的影响，它的 MAP 相当低，这意味着该策略在 MM 上取得成功，而不会使交易者面临高库存风险。 另请注意其 PnL 分布的峰度值显着降低，表明尾部较细，这是风险管理目的的理想属性，以及略小的 PnL 分布偏度。 我们还观察到，Jarque-Bera 检验结果表明所有策略与零假设（PnL 分布的正态性）不一致。 有趣的是，比较 SYM 和 LIN 策略，后者以较低的预期 PnL 为代价表现出较低的风险，类似于 AS 研究 [1] 的结果。 所有策略的终端库存分布都以零为中心，展示了 MM 行为的明显迹象（头寸围绕零库存波动）。 我们观察到 DRL 和 LIN 策略对应的终端库存分布看起来非常相似，表明具有可比性的风险偏好。 相反，注意SYM策略对应的绝对平均终端库存分布的大小，清楚地表明其无视库存风险。 下图描绘了 DRL 策略在时间上的平均性能以及相关的置信区间，平均 PnL 随时间（看似）线性增长。

敏感性分析

理想情况下，我们希望获得对潜在订单到达强度率的变化具有鲁棒性的 MM 控制。 相关地，我们通过改变所有订单类型的背景强度率来对 DRL 控制器进行灵敏度分析——特别是通过添加正常（高斯）噪声。更准确地说，考虑了三种不同的噪声大小——基于均值 0 和方差 0.1 (DRLN-0.1)、方差 0.2 (DRL-N-0.2) 和方差 0.3 (DRLN-0.3) 的高斯噪声。 结果示下表。

显然，较大的扰动会增加终端 PnL 分布的标准偏差，而对均值的影响则更为复杂，最大的噪声大小会导致最大的均值 PnL（以及 MAP）。 不出所料，随着扰动大小的增加，夏普比率明显下降（而 MAP 增加）。此外，我们调查了我们的策略和基准策略在不同交易成本下的表现。 下图显示了三种策略的夏普比率和可变限价单交易费率。

从图中可以清楚地看出，DRL 策略能够容忍包含限价订单交易的费用，最高可达 0.6% 左右的费用。 相反，LIN 策略已经产生负利润，费用设置为 0.4%，而 SYM 策略对此类交易费用的容忍度极低，即使是相对较低的 0.2%。 所考虑的比率处于现实范围内，因此这验证了我们的 DRL 方法在实盘条件下的性能。 最后，我们在不同的限价订单交易费用下重新训练 DRL 控制器，并调查相应的平均交易数量。 在限价订单交易成本分别为 0%、0.2%、0.4% 和 0.6% 的情况下，平均交易笔数分别为 24.54、15.0、11.28 和 7.85。 结果清楚地表明，较高的限价订单交易成本，正如预期的那样，会导致较少的已实现交易（交易），因为 DRL 控制器在存在高交易成本的情况下越来越区分何时以及是否发布限价订单。

结论与代码

与启发式基准相比，基于 DRL 的方法可用于获得具有卓越性能的做市策略。 当采用基于多变量霍克斯过程的现实 LOB 模拟器时，该方法会产生可喜的结果。 特别关注由此产生的 PnL 和终端库存分布的统计分析，以及对基础订单强度率和限价订单费用变化的敏感性分析。 我们得出结论，DRL 提供了一种获得有竞争力的 MM 控制器的可行方法。 进一步的研究可能会考虑更高级的 MM 模型，这些模型考虑了完整的限价订单簿，或者基于具有替代（幂律或多项式）内核的霍克斯过程。 最后，鲁棒的对抗性 RL [31] 可用于进一步提高模型不确定性下的泛化和鲁棒性。

本文配套代码（Python），关注wx工中浩 数量技术宅 ，回复关键词：强化学习做市，即可获取。

参考文献

[1] Avellaneda, M. and Stoikov, S., 2008. High-frequency trading in a limit order book. Quantitative Finance, 8(3), pp.217-224.

[2] Fodra, P. and Pham, H., 2015. High frequency trading and asymptotics for small risk aversion in a Markov renewal model. SIAM Journal on Financial Mathematics, 6(1), pp.656-684.

[3] Gu´eant, O., Lehalle, C.A. and Fernandez-Tapia, J., 2013. Dealing with the inventory risk: a solution to the market making problem. Mathematics and financial economics, 7(4), pp.477-507.

[4] Cartea, A., Jaimungal, S. and Ricci, J., 2018. Algorithmic trading, stochastic control, and mutually exciting processes. SIAM Review, 60(3), pp.673-703.

[5] Silver, D., Huang, A., Maddison, C.J., Guez, A., Sifre, L., Van Den Driessche, G., Schrittwieser, J., Antonoglou, I., Panneershelvam, V., Lanctot, M. and Dieleman, S., 2016. Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), pp.484-489.

[6] Ranzato, M.A., Chopra, S., Auli, M. and Zaremba, W., 2015. Sequence level training with recurrent neural networks. arXiv preprint arXiv:1511.06732.

[7] Demirel, B., Ramaswamy, A., Quevedo, D.E. and Karl, H., 2018. Deepcas: A deep reinforcement learning algorithm for control-aware scheduling. IEEE Control Systems Letters, 2(4), pp.737-742.

[8] Lim, Y.S. and Gorse, D., 2018, April. Reinforcement learning for high-frequency market making. In ESANN 2018-Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (pp. 521-526). ESANN.

[9] Cont, R., Stoikov, S. and Talreja, R., 2010. A stochastic model for order book dynamics. Operations research, 58(3), pp.549-563.

[10] Spooner, T., Fearnley, J., Savani, R. and Koukorinis, A., 2018. Market making via reinforcement learning. arXiv preprint arXiv:1804.04216.

[11] Sadighian, J., 2019. Deep reinforcement learning in cryptocurrency market making. arXiv preprint arXiv:1911.08647.

[12] Gaˇsperov, B. and Kostanjˇcar, Z., 2021. Market Making With Signals Through Deep Reinforcement Learning. IEEE Access, 9, pp.6161161622.

[13] Baldacci, B., Manziuk, I., Mastrolia, T. and Rosenbaum, M., 2019. Market making and incentives design in the presence of a dark pool: a deep reinforcement learning approach. arXiv preprint arXiv:1912.01129.

[14] Gu´eant, O. and Manziuk, I., 2019. Deep reinforcement learning for market making in corporate bonds: beating the curse of dimensionality. Applied Mathematical Finance, 26(5), pp.387-452.

[15] Ganesh, S., Vadori, N., Xu, M., Zheng, H., Reddy, P. and Veloso, M., 2019. Reinforcement learning for market making in a multi-agent dealer market. arXiv preprint arXiv:1911.05892.

[16] Law, B. and Viens, F., 2019. Market making under a weakly consistent limit order book model. High Frequency, 2(3-4), pp.215-238.

[17] Bacry, E., Mastromatteo, I. and Muzy, J.F., 2015. Hawkes processes in finance. Market Microstructure and Liquidity, 1(01), p.1550005.

[18] Lu, X. and Abergel, F., 2018. High-dimensional Hawkes processes for limit order books: modelling, empirical analysis and numerical calibration. Quantitative Finance, 18(2), pp.249-264.

[19] Da Fonseca, J. and Zaatour, R., 2014. Hawkes process: Fast calibration, application to trade clustering, and diffusive limit. Journal of Futures Markets, 34(6), pp.548-579.

[20] Lopez de Prado, M., 2019. Tactical investment algorithms. Available at SSRN 3459866.

[21] Embrechts, P., Liniger, T. and Lin, L., 2011. Multivariate Hawkes processes: an application to financial data. Journal of Applied Probability, 48(A), pp.367-378.

[22] Law, B. and Viens, F., 2016. Hawkes processes and their applications to high-frequency data modeling. Handbook of High-Frequency Trading and Modeling in Finance, 9, p.183.

[23] Biais, B., Hillion, P. and Spatt, C., 1995. An empirical analysis of the limit order book and the order flow in the Paris Bourse. the Journal of Finance, 50(5), pp.1655-1689.

[24] Filimonov, V. and Sornette, D., 2015. Apparent criticality and calibration issues in the Hawkes self-excited point process model: application to high-frequency financial data. Quantitative Finance, 15(8), pp.12931314.

[25] Simon, G., 2016. Hawkes Processes in Finance: A Review with Simulations (Doctoral dissertation, University of Oregon).

[26] Oakes, D., 1975. The Markovian self-exciting process. Journal of Applied Probability, 12(1), pp.69-77.

[27] Ogata, Y., 1981. On Lewis’ simulation method for point processes. IEEE Transactions on Information Theory, 27(1), pp.23-31.

[28] Briola, A., Turiel, J. and Aste, T., 2020. Deep Learning modeling of Limit Order Book: a comparative perspective. arXiv preprint arXiv:2007.07319.

[29] Gu´eant, O., 2016. The Financial Mathematics of Market Liquidity: From optimal execution to market making (Vol. 33). CRC Press.

[30] Coates, J.M. and Page, L., 2009. A note on trader Sharpe Ratios. PloS one, 4(11), p.e8036.

[31] Pinto, L., Davidson, J., Sukthankar, R. and Gupta, A., 2017, July. Robust adversarial reinforcement learning. In International Conference on Machine Learning (pp. 2817-2826). PMLR.