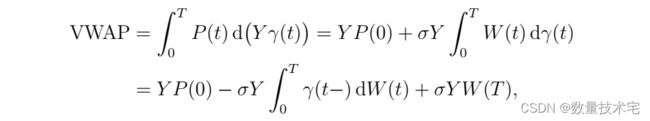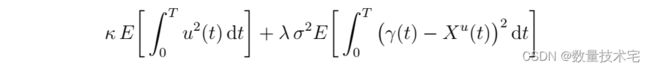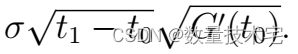VWAP 订单的最佳执行方法：随机控制法

数量技术宅团队在CSDN学院推出了量化投资系列课程

欢迎有兴趣系统学习量化投资的同学，点击下方链接报名：

量化投资速成营（入门课程）

Python股票量化投资

Python期货量化投资

Python数字货币量化投资

C++语言CTP期货交易系统开发

数字货币JavaScript语言量化交易系统开发

---

引言：相关研究

在当今的投资领域，算法交易正迅速成为客户获取和清算股票头寸的首选方法。 通常，被委托者会根据客户选择的基准，使用基于计算机的算法来买入（或卖出）头寸。 这些算法中最古老和最流行的算法之一是 VWAP（成交量加权平均价格）。 VWAP 基准在经纪商和客户中的受欢迎程度有几个原因。 首先，它的计算非常简单，便于轻松进行交易后报告。 其次，它鼓励将较大订单拆分为较小订单，减少对大量流动性的需求，从而减少市场影响/波动。 最后，给定一个时间间隔，它被认为是“公平”基准价格，用[4]的语言来说，VWAP是一个价格，是任何随机选择的非战略交易者可以实现的价格的无偏估计 。因此，击败市场 VWAP 将被视为“良好”的交易执行。

本文提出了一种随机控制方法来解决经纪商应如何优化安排 VWAP 基准交易的问题。 实际上，客户指定买入（或卖出）数量以及开始和结束时间，然后经纪商必须获取（清算）头寸，试图将成交量加权价格与交易量加权价格之差的均值和方差最小化。 订单生命周期内的市场成交量加权平均价格（滑点）。 当前研究的主要动机是试图提高执行效率。 由于通过算法进行的名义交易量巨大，应用所获得的结果所产生的微小收益可能会导致经纪商及其客户的利润大幅增加。

文献[5]对到达价格基准的最优执行问题进行了深入研究，另请参阅 Almgren 及其合著者的开创性论文 [1]、[2] 和 [3]。 相比之下，也许由于基准的随机性，与当前问题相关的文献明显较少。 该领域的第一篇工作是 Konishi [23] 的文章，他推导了当价格由布朗运动给出时单一和篮子 VWAP 执行的最佳执行轨迹。 然后根据东京证券交易所的实际交易数据对该策略进行评估。 在本文之后，VWAP 跟踪已受到多种不同方法的攻击。 McCulloch 和 Kazakov [26] 将其视为部分信息下的二次对冲问题，而 Kakade 等人。 [21] 和 Bia lkowski 等人。 [6] 使用在线学习和动态交易量方法，HumpheryJenner [20] 给出了考虑日内噪音的 VWAP 交易规则。 最后 Bouchard 和 Dang [8] 将其表述为随机目标问题，并推导出值函数的粘度解表征。 请注意，上述文章（不包括[8]）没有考虑交易对市场的影响，也没有对日内成交量曲线强加任何参数结构。

本文有几个贡献。 首先，我们通过允许线性临时市场影响模型扩展了该领域的先前文献。 理论上已经研究了更一般的价格影响模型，例如 通过 Gatheral [14]，并根据经验，例如 布绍等人。 [9]（参见 Gatheral 和 Schied [16] 以获得更好的概述）然而，线性模型导致了一个易于处理的问题。 其次，我们提供了一个相对量的参数模型，该模型非常适合真实数据，反映了有意义的潜在经济假设，同时易于处理以执行优化。 最后，虽然由于使用 VWAP 作为基准而涉及优化问题，但我们能够明确地表征最优控制，从而为最优交易率提供封闭式解决方案。 这一最终结果首次开辟了一种严格的数学方法来确定有保证的 VWAP 交易的佣金，类似于 [2] 中针对实施缺口所做的方法。

本文的结构如下。 在下一节中，我们将介绍并证明我们的模型是正确的，该模型使用 VWAP 作为最佳交易执行的基准。 我们在第 3 节定理 3.1 中介绍了主要结果，它为最优交易率提供了显式解。 将证明推迟到第 5 节，我们在第 3 节中解释了最优交易率的两个关键属性。 它的符号只能从负变为正一次，而不能从负变为正，并且最优交易率可以分解为两部分，一部分是确定性 TWAP（时间加权平均价格）策略，另一部分反映由于 相对体积曲线的跳跃。 在第 4 节中，我们展示并讨论参数模型与交易量的拟合程度。

使用 VWAP 基准的框架

在这里，我们描述模型的公式和关键假设。 我们从我们的交易策略开始，不失一般性，我们考虑 Y 股的购买计划。 卖出的情况可以通过时间倒转来考虑。

交易成本

客户给我们一个开始和结束时间，我们假设（不失一般性）分别由 t0 = 0 和 T 给出。 我们必须在T之前完成股票的购买，并将以[0;T]期间的市场VWAP为基准，为简单起见，读者可能认为T=1，对应于一天的VWAP订单。 按照文献中的标准，我们研究过滤概率空间 (Ω; F; (Ft)0≤t≤T; P) 满足正确连续性和完整性的通常假设，并且我们用 Xu(t) 表示我们的份额 t 处的持有量，其中交易策略 u 是一个经过调整且可积分的过程，通常称为交易率。 特别是我们的持有量根据： dXu(t) = u(t) dt; Xu(0) = 0; Xu(T) = Y

资产价格过程 P(t) 0≤t≤T 假设为算术布朗运动： P(t) = P(0) + σW(t)

其中 σ > 0 表示每日波动性，W(t) 0≤t≤T 是 (Ω; F; (Ft)0≤t≤T; P) 上的标准布朗运动。 在当前设置中使用算术而不是几何布朗运动是可能的，因为我们正在考虑日内交易范围，因此 P(t) 为负值的概率极小，并且两个模型之间的差异可以忽略不计，请参阅 Gatheral 和 Schied [15]。

众所周知，当我们进行交易时，我们并没有意识到上述价格 P(t)（可以将其视为中间报价），而是支付： Pu(t) = P(t) + κu(t)

其中 κ 是线性（临时）市场影响模型的系数。 它代表了由于我们交易速度而产生的瞬时线性溢价。 该模型（以及许多更复杂的模型）在文献中进行了详细研究，请参阅 Gatheral [14] 或 Bouchaud 等人。 [9]。 线性形式是必要的，因为它会导致二次交易成本，从而产生一个易于处理的问题。 然而，还需要注意的是，鉴于市场影响模型的预测精度极低（通常< 5% R2），因放弃线性模型而增加复杂性的成本将超过更好地描述市场影响所带来的任何收益。 此外，Cont 等人最近的实证研究也支持线性价格影响。 [11]。 上面将一些对影响的依赖引入到解决方案中，这就是它的目的。

与 Almgren [1] 的第 1.1 节类似，我们使用控制 u 购买股票 Y 的总支出 TEu 由下式给出：

​

我们应用关系式，使用Xu(T) = Y 并且 Xu 具有有限变分，乘积规则得出

VWAP 基准

给定一系列价格 (Pi)i=1,...,N 以及以这些价格执行的交易量 (Vi)i=1,...,N，VWAP 定义为

如果我们定义 Vi 作为累积交易量，我们有

我们选择通过伽玛桥对日内相对成交量曲线进行建模有几个原因。首先，我们将在第 4 节中看到，我们的模型非常适合真实股票数据，前提是股票的交易流动性足够，并且变化有限，就像真实数据一样。其次，我们可以将累计交易量视为类似于坝雨的积累，类似于Gani [13]将保险索赔的到来视为类似于坝雨的积累。后者可以通过 Moran [27] 指出的伽玛过程进行建模，因此类似地，相对量将是伽玛桥。最后，如果我们假设交易量在一天中是独立且平稳分布的，并且相对日内交易量与总交易量无关，那么我们可以证明日内交易量曲线一定是伽马桥。该链接基于以下有关伽玛过程的理论结果。

相对交易量曲线与总交易量无关的假设并非太不现实；很难想象某一天的相对交易量曲线很大程度上取决于该天的总交易量。图 1 左图的美国和欧洲主要股票支持了这一点。使用伽玛过程对交易量进行建模并使用布朗运动对价格进行建模的结果是它们相互独立；参见 Kallenberg 的引理 15.6 [22]。图 1 的右图显示，成交量和价格变化之间的日内相关性变化很大，但平均而言很小。因此，很难将其纳入模型中，导致性能的潜在提高很小，从而证明独立性假设的合理性。

图 1：沃达丰和微软股票在 2012 年前 100 个交易日内的相对交易量和总交易量之间的相关性（左图）以及日内交易量和价格变化之间的相关性（右图），使用 5 分钟盘中数据

纵观历史交易量数据并注意其间歇性，交易量独立且全天稳定分布的假设是理想化的。然而，我们可以将伽马桥视为真实相对体积曲线的零阶近似，如果这样的假设成立，这将是准确的。然后，这提供了一个易于处理的基础，在此基础上可以合并更现实的功能。最后一点，让我们注意到，与实际数据的拟合足够好，可以得出这样的结论：偏离这种假设的影响（也许令人惊讶）不太大。

由于我们只会考虑伽玛桥而不考虑其底层伽玛过程，因此通过缩放我们可以（并且今后确实）设置 θ = 1 而不失一般性。而且，在后面的模拟中，我们固定T = 1并使用m作为模型参数。在相对成交量曲线采用伽玛桥的假设下，购买市场 VWAP 的 Y 股的支出（以美元计）由下式给出

我们的论证与（1）的推导类似。 VWAP 基准应被视为订单生命周期内的平均市场价格，它忽略了市场影响，因为中间报价代表了对当前公平市场价格的合理估计。观察到我们可以按 1/Y 缩放，因此我们可以（并且确实）假设客户想要购买 1 股。

人们可能会反对模型公式，因为 L(T) 是未知的。虽然这是一个有效的反对意见，但它误解了本文的目标。所有从事算法交易的主要经纪商都需要日内相对交易量曲线的模型。此类模型的主要应用是执行 VWAP 和 PVol（交 易量百分比）订单。

交易量加权平均价格=可测映射 x → x/(1 - x)。根据卢卡奇比例和独立定理 [24]，A 和 B 都具有伽马分布。在评估此类模型在交易应用程序中的可行性时，可以将使用新模型时的性能与“完美信息”情况下的性能进行比较，此处通过伽玛桥进行建模。这里提出的框架允许针对这种情况提供封闭式解决方案，从而允许以与其用途相关的方式评估新的体积曲线模型，而不仅仅是纯粹的拟合优度测试。第二个好处是在交易后分析中，这里提出的解决方案为 VWAP 交易的执行提供了一个独立于经纪商的基准，允许进行相对比较以及共同的绝对表现。我们将在未来的工作中解决比较和评估不同 VWAP 策略的问题。总之，这里的重点不是用于交易 VWAP 的实时（即基于相对交易量的自适应估计器）策略，而是努力建立一个框架，在该框架中人们可以获得针对交易量的封闭式且可实施的解决方案。 VWAP 交易问题可用于设置性能上限并提供独立于经纪商的基准。因此，我们正在使用的过滤(Ft)0≤t≤T使得伽马桥 γ(t) 和布朗运动 W(t) 适应它。读者会注意到，在计算相对成交量曲线时，我们的交易没有被考虑在内，因此它变成了外生的。这显然是一种简化，实际上相当于假设（非标准化）规模 Y 相对于总交易量较小，即我们正在处理小订单。由于典型的算法交易 VWAP 订单的有效规模（按天计算）为每日交易量的 10‑15%，因此这一假设并没有太大的限制性，并且极大地简化了所考虑的问题。正如 Hu [19] 所解释的，他分析了有和没有自己交易的 VWAP 的差异，甚至可能需要将我们自己的交易从市场VWAP 计算中排除，以便将我们的表现与不受我们影响的基准进行比较。大型 VWAP 交易（>50% 日交易量）的有趣案例将在其他地方考虑。

算法性能

现在股票数量已标准化为 Y = 1，我们的成本可以视为以美元计算的每股成本。我们的首要目标是最小化预期滑点，定义为 ：

从经纪商的角度来看，仅仅拥有较小的预期滑点虽然很好，但并不是唯一的目标。从交易后的角度来看，如果发生这种情况，有必要向客户解释为什么滑点与预期相差甚远。因此，我们的第二个目标是尝试最小化滑点的方差。我们使用近似

其中，我们假设最后一个方程是平方可积鞅，并使用 γ 是有界的并且只有可数个跳跃，这种近似的主要原因是易于处理，否则难度将显着增加。数学原因：原问题的难点在于其时间不一致。正如 Bjork 和 Murgoci [7] 的 1.2 节中所解释的，E[X] + λVar[X] 形式的均值方差问题的时间不一致是由Var[X] 中的项 (E[X])2 引起的] = E[X2 ] - (E[X])2 。虽然标准时间一致问题允许具有诸如E[X2 ]之类的非线性函数的期望值，但是项(E[X])2是期望值的非线性函数而不是非线性函数的期望值。然而，在我们的特定问题中，时间不一致是轻微的，因为 Var[slipu ] 的值接近均值为零的 γ(t)- Xu (t) dW(t)，因此导致方差时间一致的配方。因此，这种近似适合我们的情况。

因此，我们研究最小化

作为均值方差问题的近似

对于给定的均值‑方差权衡参数 λ > 0。在进一步证明该近似值的合理性中，我们注意到与 Almgren [1] 和 Konishi [23] 类似，Var[slipu ] 的主要驱动因素通常是成交量曲线γ 而不是交易率 u，这样我们就捕 获了主导项。 为了了解近似误差，我们使用了蒙特卡洛模拟。

读者会注意到，我们没有考虑当前模型中的拍卖。事实上，我们已经为所谓的“连续”（非拍卖）交易阶段执行的订单制定了 VWAP 跟踪问题。对于美国股票来说，简单地忽略拍卖是一个合理的近似值，因为那里的平均交易量只占总交易量的一小部分。在拍卖量通常要高得多的欧洲，人们可以想象对上述框架进行一个小修改，其中将使用动态模型来估计公开拍卖和收盘拍卖中执行的部分，然后可以使用上述模型来执行剩余部分。由于本文的重点不是拍卖量的预测，因此我们假设在初步步骤中已使用历史平均值，并且交易总量已相应减少，因此此处提供的结果同样适用于美国和美国欧洲股票。

重要结果

我们的主要结果是价值函数 v 和（2）中最优控制的明确表征。价值函数 v 由下式给出

最优控制 u 和相应的持股量 X 由下式给出

假设我们用近似问题替换（2）

现在观察没有固定的终止条件。利用 γ 是 [tm, Tm] 上的伽马桥，其基本平均增长率等于 1，根据 Emery 和 Yor [12] 的推论 1，给出了伽马桥 γ 的无穷小生成器经过

其中 f 是R+上的函数，在紧致上具有有界变化。如果我们假设 v n足够规则，它应该满足

由于二次结构，我们提出

请注意，我们的主要结果给出了最优交易率 u 和最优持有量 X 的明确公式。这个理想的X公式是由于我们要求持有量相对于 t 绝对连续。相比之下，McCulloch 和 Kazakov [26] 并没有强制执行这一点，因此人们可能不会直接将他们的结果与我们的结果进行比较。

最佳交易率取决于交易量曲线，而不取决于价格过程。我们给出一些直觉来解释为什么这是使用 VWAP 优化标准和 Brown ian 价格过程的自然结果。在比较两种策略的 VWAP 时，只有价格变动相关，而不是价格过程的绝对水平相关。由于在我们的模型中，价格变动独立于过去的价格（它们由布朗增量给出），因此有关过去价格的信息不包含在最优策略中。

现在让我们更详细地描述最优控制的结构。 直观上很明显应该有一个买入和卖出区域； 更准确地说，从 (3) 可以看出 ^ u(s) 的符号取决于 X^(s)。 特别地，u^(s) 为正当且仅当 X^(s) < −b(s)2γa((ss))−c(s) 时。 事实上，如果我们持有的 X^(s) 较低，我们将进行购买以接近我们的目标，而对于较高的 X^(s)，暂时减少持有以接近 γ(s) 可能是有益的。 这导致我们通过以下方式定义边界。

一个关键的实际要求是，对于最初的购买计划（即当我们从 0 股开始时），我们不应该出售。事实上，如果在执行过程中股票持有量不是单调增加，大多数客户通常会感到不满。此外，在美国市场，这种行为实际上是受到监管机构禁止的。1以下命题表明，在我们的公式中，对于任何参数值，情况确实如此，强调了模型的适用性以及对这一重要监管方面的合规性。

第二部分的思想是，当过程X(t)低于z(t)时，γ(t) 会与 z(t) 相交； 由于边界 z 的特性，稍后时间点的 γ(s) 。 图 2 说明了 X的这种行为，即它只能从上方穿过 ze，而不能从下方穿过 ze。 我们还可以看到，对于不同的起点，X的路径在很短的时间后就处于非常相似的轨迹上。

将模型拟合到数据

为了使基于伽马桥的模型适合数据，可以尝试使用例如最小二乘法来拟合 m。我们注意到，由于 E[γ(t)] = 这一拟合必须根据方差或标准差进行，因此当天伽马桥的平均增量与 m 无关。实际上，众所周知，交易量是 U 形的（当天开始和结束时的交易量较高），这意味着累积相对交易量呈近似立方体形状，请参见图 5。为了将此功能纳入我们的模型中，我们制作了一个由多项式给出的确定性时间变化。

对于一些常数 a、b、c、d。我们要求 G 是 [0, T] 的递增双射，因此我们有 d = 0 且 c = 1- aT2 - bT。在下一小节中，我们讨论如何选择参数 a、b 和 m 来拟合数据。在第4.2 节中，我们解释了这个时间变化如何影响我们的模型和结果。

估计模型参数

我们以沃达丰集团 (VOD) 和微软 (MSFT) 股票的参数估计为例。我们还分析了其他股票，流动性好的欧洲和美国股票的结果也类似。 我们使用以 5 分钟频率观察的日内成交量，这是成交量预测的合理持续时间，尽管以下参数对此选择不敏感。 我们应用了一种使用非线性回归计算的矩估计方法，并基于 2012 年前 60 个交易日的盘中交易量曲线的一阶和二阶矩。由于对于我们的问题，相对交易量而不是绝对交易量是相关的，因此我们研究 与相对体积的拟合。 图 3 显示了最终的曲线，从而得出了估计值：

我们在图 3 中看到，鉴于我们只有三个模型参数，我们总体上很好地拟合了日内成交量曲线的平均值和标准差。

为了验证模型没有表现出任何极端的季节性依赖性，我们在接下来的 30 天中使用 60 天的滚动窗口校准了参数 a、b 和 m。 时间序列如图 4 所示。请注意，伽玛桥的方差与 1/(mT1+1) 成正比，因此 m 的大范围并不像最初假设的那么严重。

接下来我们不仅讨论当前的适合度，而且讨论一般的适合度。 在第一个定性分析中，我们可以使用估计参数将 60 个交易日的日内成交量曲线与基于伽马桥的 60 个轨迹样本进行比较，并使用估计的参数进行时间变化。 我们在图 5 中看到，真实轨迹和样本轨迹的模式看起来很相似，尽管模拟路径的行为更加不稳定。

为了做出更定量的陈述，我们考虑两个拟合优度检验。我们再次使用上表中给出的基于 2012 年前 60个交易日的估计参数 a、b 和 m。然后，我们将接下来的 30 天作为样本外测试数据集。根据我们对相对体积的伽玛桥的假设，我们在每个时间 t 都有 30 个来自带有参数的 beta 分布的独立同分布观测值

第一个检验使用样本平均值近似正态分布，平均值为 α(t)/(α(t)+β(t))，方差由中心极限定理确定。 执行 z 检验会得到如图 6 所示的 p 值。

第二个检验（也显示在图 6 中）是众所周知的 Kolmogorov Smirnov 检验，它评估样本是从 Beta(α(t),β(t)) 分布中抽取的原假设。观察到我们现在考虑整个经验累积分布，而不仅仅是样本均值。由于不同时间点之间存在依赖性，因此应按以下方式解释图 6：如果随机选择一天中的一个时间间隔，则相应的 y 值就是该给定时间的两个检验的 p 值。一般来说，早上我们不会拒绝原假设，而下午的部分时间我们会拒绝原假设。一天中某些时间不完美的结论并不令人惊讶。事实上，相对体积并不是以伽玛桥的形式分布的，而是受到模型没有（也不能）完全捕获的特殊因素的影响。这里提出的模型旨在捕捉主要的风格化特征，同时足够易于优化，与使用布朗运动作为价格模型进行比较，尽管回报率非高斯性以及期权定价的布莱克‑斯科尔斯框架。考虑到这些因素，我们得出结论，该模型适合我们的目的。

与将模型拟合到数据相关的最后一点涉及参数 κ 和 λ 的选择。 计算表明，我们的模型公式的一个结果是，当 κ不等于0 时，由于成本消失，我们最终能够完美地跟踪 VWAP。 在真实的交易环境中，这当然是不可能的，因为每次执行市价订单都会产生价差一半的每股成本（相对于中间报价）。 解决这个问题的一种方法是重新制定影响成本，将其一半的固定成本包括在内。 这自然会导致脉冲控制公式超出了本文的范围。 更实用的解决方案观察到驱动最优控制/轨迹的关键参数是 k/λσ2 。 因此，在实践中，人们可以简单地选择 λ 的值，以使该比率处于模型适用的适当范围内。 从广义上讲，我们选择一个有效的 λ" 来考虑点差成本，类似于 [2] 中描述的采用实施缺口框架的交易系统中所做的操作。

将时间变化集成到模型中

正如我们在上面的讨论中所看到的，伽玛桥与相对体积曲线很好地拟合，但前提是经过确定性时间变换。 接下来我们看到，当模型经历这样的时间变化时，我们的主要结果仍然成立。 我们首先用一个简单的例子解释原因，然后给出数学论证。 假设已经计算出第2节模型中的最优控制和价值函数。现在可以看出，除了后半天的预期交易频率是前半天的两倍之外，模型拟合良好。 最优交易策略应该如何修改？ 一个自然的答案是通过简单地改变交易执行的速度来相应地扩展原始策略。 早上，它会减少三分之一，这样在一天的中间，人们的仓位就与采用原始策略的一天三分之一后的仓位相同。 下午交易频率则相应增加。 综上所述，新策略只是时间变化后的原始策略除以时间变化的导数。

期望优化问题的值不会改变也是明智的，因为算法性能（VWAP 的最小滑点）在确定性时间变化下不应改变。事实上，我们在选择策略时可能会考虑时间变化，这样就不会出现额外的信息。当然，这些论点认为时间变化是确定性的，因此是提前已知的，然而这对于大多数实际目的来说是可以接受的。

现在让我们通过调整第 2 节的模型来使上述论证更加严格。假设时间变化由可微的确定性函数 G 给出：[0, T] → [0, T]，其中 G(0) = 0， G(T) = T 且 G (t) ≥ C 对于某个常数 C > 0 且所有 t ∈ [0, T]。相对体积曲线由 η(t) = γ G(t) 建模，其中 γ(t) 是伽马桥，其基础伽马过程具有通用参数 m。时间变化意味着交易频率取决于一天中的时间，例如，在一天的开始和收盘时交易频率较高。

交易量和价格之间存在众所周知的联系，因此我们预计不同的交易频率也会影响价格过程，因此时间 t 时的资产价格等于：

观察现在我们有两个时间点 t0 和 t1，收益的波动性与

假设差值 t1 − t0 很小且固定，可以近似为

由于 G'反映了预期的日内交易频率，因此它通常是 U 形的，因此 根号G' 也是 U 形的（或 V 形的）。事实上，U形G'意味着它的导数G‘’开始时为负，最后增加为正。因此，我们预计瞬时波动呈 U 形。 除了对我们的模型进行时间改变的数学结果之外，这种现象在许多不同股票市场的实证金融文献中都有很好的记录，可以追溯到 Wood 等人 [28]和哈里斯[17]。 此外，U 形形式的盘中交易量与波动性之间的联系是众所周知的，并且至少可以追溯到 Harris [18]。 常见的理论解释是，交易量和波动性的模式都与信息流有关，而信息流不随时间变化。 例如，在参与者信息不对称的市场中，交易量本身就传递着信息，因此U形的交易量将导致U形的信息流。 我们的模型通过时间变化捕获这种非恒定的信息流。

同样，t 时刻的市场影响系数现在为 κ(t) = κ/G'(t)，因为 G0'的减少（或增加）意味着整体市场交易频率的减慢（加速），因此 我们的交易量增加（减少）。按照与第 2 节相同的思路进行，并另外使用 d = dG(s) = G'(s) ds，我们看到优化问题的新值函数由下式给出

由于这对于任何这样的 y 都成立，我们得到

其中 v 是 (2) 中的原始值函数，其特征如定理 3.1 所示。 我们还可以看到时变问题的最优控制由下式给出：

写在最后

由于 时间与精力 有限，我们选取了原论文中我们认为核心的部分进行了整理和翻译。本文原文英文文献与配套代码（Python），关注wx工中浩 数量技术宅 ，回复关键词：VWAP，即可获取。