数据结构(四)树
本文是在原本数据结构与算法闯关的基础上总结得来,加入了自己的理解和部分习题讲解
原活动链接
邀请码: JL57F5
目录
- 树
-
- 1. 树的结构和性质
- 2. 广度优先搜索
- 3. 深度优先搜索
-
- 删除拥有两个子节点的节点步骤:
- 图示说明:
- 使用左子树的最大节点作为替代者的步骤:
- 右子树的最小节点
- 左子树的最大节点
- 4. 案例*:删除二叉查找树中的某个节点的代码示例
-
- 示例树结构
- 演示删除操作
- 5. 案例:二叉查找树的算法(4的总结)
- 6. 案例*: 如何利用二叉查找树实现“商城查找”业务需求
- 7. 闯关题
-
- 根据要求完成题目
- 案例*:二叉查找树实现简单的联系人管理系统的实现代码
树
1. 树的结构和性质
其实, 在现实生活中也存在类似的结构。例如,在一个公司中员工架构最顶端是CEO,CEO的下面有若干副总,每个副总下面有若干部门经理,每个部门经理下面有若干基层员工。这种员工架构很容易用树这种数据结构来表示。
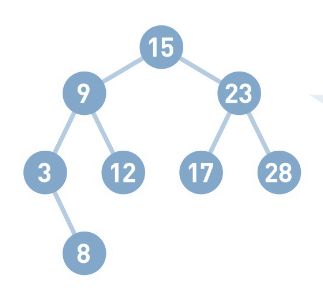
二叉查找树(又叫作二叉搜索树或二叉排序树)是一种数据结构,采用了图的树形结构。 数据存储于二叉查找树的各个结点中。
请记住: 树是一种特殊的图, 它是一种无向无环的图,其中每个节点只有一个父节点,而图则没有这些限制,节点之间可以有任意的连接关系。
这就是二叉查找树例子。结点中的数字便是存储的数据。
二叉查找树有两个性质。大家注意 !
第一个是每个结点的值均大于其左子树上任意一个结点的值。比如结点9大于其左子树上的3和8。
第二个是每个结点的值均小于其右子树上任意一个结点的值。比如结点15小于其右子树上的23、17和28。
根据这两个性质可以得到以下结论。首先,二叉查找树的最小结点要从顶端开始,往其左下的末端寻找。此处最小值为3。
反过来,二叉查找树的最大结点要从顶端开始,往其右下的末端寻找。此处最大值为28。
2. 广度优先搜索
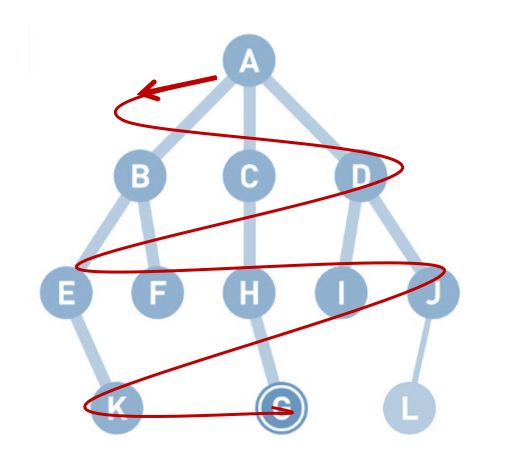
广度优先搜索会优先从离起点近的顶点开始搜索。
A作为起点, 现在想要找到G点, 根据广度优先我们可以这么做…
这个示例中的搜索顺序为A、B、C、D、E、F、H、I、J、K、G
广度优先搜索的特征为从起点开始,由近及远进行广泛的搜索。因此,目标顶点离起点越近,搜索结束得就越快。
3. 深度优先搜索
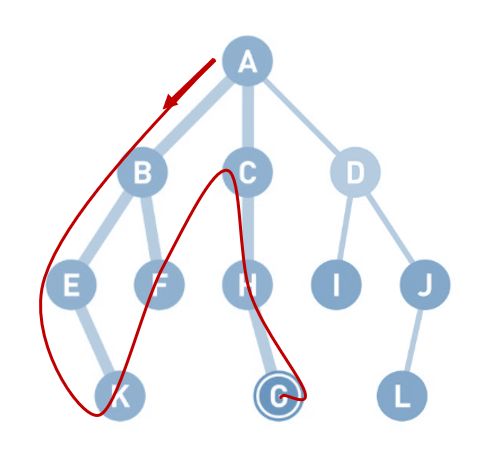
深度优先搜索会沿着一条路径不断往下搜索直到不能再继续为止,然后再折返,开始搜索下一条候补路径。
这个示例的搜索顺序为A、B、E、K、F、C、H、G
深度优先搜索的特征为沿着一条路径不断往下,进行深度搜索。
虽然广度优先搜索和深度优先搜索在搜索顺序上有很大的差异,但是在操作步骤上却只有一点不同,那就是选择哪一个候补顶点作为下一个顶点的基准不同。
广度优先搜索选择的是最早成为候补的顶点,因为顶点离起点越近就越早成为候补,所以会从离起点近的地方开始按顺序搜索;
而深度优先搜索选择的则是最新成为候补的顶点,所以会一路往下,沿着新发现的路径不断深入搜索。
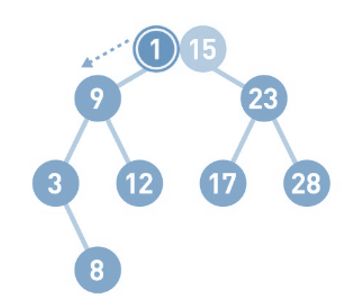
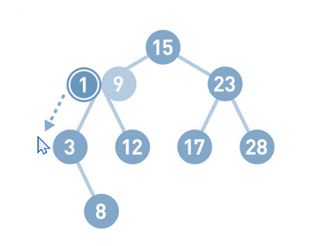
下面我们来试着演示一下往二叉查找树中添加数据。比如添加数字1
将想要添加的1与该结点中的值进行比较,小于它则往左移,大于它则往右移。
由于1<9,所以将1往左移。同理 , 由于1<3,所以继续将1往左移,但前面已经没有结点了,所以把1作为新结点添加到左下方。
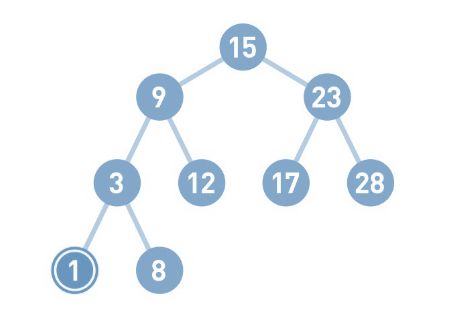
接下来,我们再试试添加数字4。和前面的步骤一样,首先从二叉查找树的顶端结点开始寻找添加数字的位置。4< 15 往左移, 由于4<9,所以将其往左移。由于4>3,所以将其往右移。
由于4<8,所以需要将其往左移,但前面已经没有结点了,所以把4作为新结点添加到左下方。
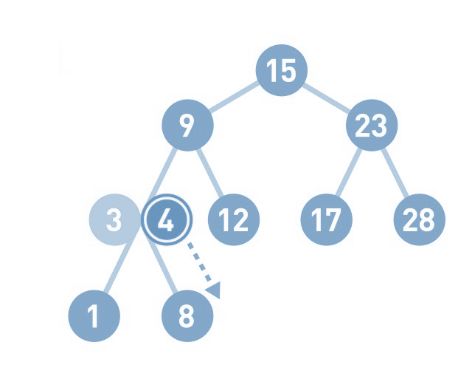
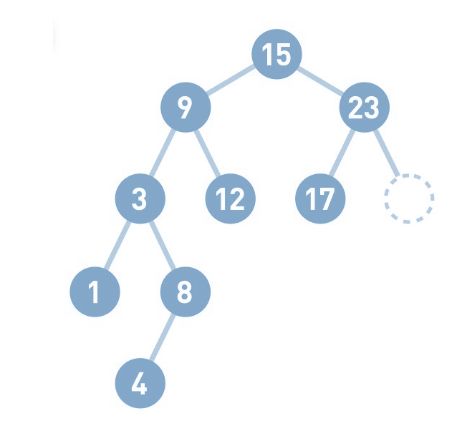
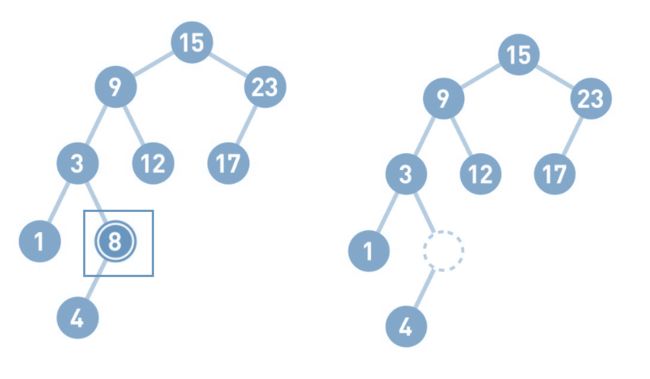
再试试删除结点8。如果需要删除的结点只有一个子结点,那么先删掉目标结点, 然后把子结点移到被删除结点的位置上即可。
注意:在二叉查找树(BST)中删除一个节点时,需要考虑的不仅仅是该节点的左右子节点,而是整个节点的位置以及它在树中的角色。删除节点的过程分为三种主要情况:
-
删除叶子节点(没有子节点的节点):这是最简单的情况。只需直接移除该节点即可,无需对其他节点进行任何操作。
-
删除只有一个子节点的节点:在这种情况下,需要删除该节点,并将其唯一的子节点连接到该节点的父节点上。
-
删除有两个子节点的节点:这是最复杂的情况。需要找到该节点的直接后继(在其右子树中最小的节点)或直接前驱(在其左子树中最大的节点),然后用这个后继或前驱节点来替换要删除的节点。替换完成后,还需要删除原来的后继节点或前驱节点,因为它已经被移动到了新的位置。
在处理第三种情况时,通常选择直接后继节点,因为在二叉查找树中找到一个节点的直接后继通常更简单。直接后继是比该节点大的最小节点,通常是该节点右子树中的最左侧节点。一旦找到直接后继,就将其值复制到要删除的节点中,然后删除原后继节点。如果后继节点有右子节点,需要将这个右子节点连接到后继节点的父节点上。
总之,删除二叉查找树中的节点可能会涉及对树的结构进行一定的调整,以确保树仍然保持二叉查找树的性质。
补充:删除的节点有两个子节点的情况
在二叉查找树(BST)中删除一个拥有两个子节点的节点是一个稍微复杂的过程,因为在删除之后需要保持树的二叉查找属性。下面是这个过程的逐步说明:
删除拥有两个子节点的节点步骤:
- 找到要删除的节点:首先需要定位到树中需要被删除的节点。
- 找到继承者:在删除节点后,需要找到一个合适的继承者(替代节点)来占据被删除节点的位置。这个继承者是:
- 要删除节点的右子树中的最小节点(即右子树的最左边的节点),或者
- 要删除节点的左子树中的最大节点(即左子树的最右边的节点)。
通常选择第一个选项,即右子树中的最小节点。
- 删除继承者原节点:将找到的继承者从其原来的位置删除。由于这个继承者是右子树中的最小节点,它最多只会有一个右子节点。
- 替换被删除节点:将继承者放置到被删除节点的位置。这涉及到更新继承者的左右子节点链接以及被删除节点父节点的链接。
图示说明:
假设我们有如下的二叉查找树,需要删除值为 20 的节点,该节点有两个子节点。
15
/ \
10 20
/ \
17 25
- 找到要删除的节点:节点
20。 - 找到继承者:节点
20的右子树中的最小节点是25(在这个例子中,25直接就是20的右子节点)。 - 删除继承者原节点:由于
25没有左子节点,我们可以直接将其删除。 - 替换被删除节点:将
25放到20的位置。
删除和替换后的树如下:
15
/ \
10 25
/
17
在这个例子中,由于继承者 25 没有左子节点,所以替换过程相对简单。如果继承者有左子节点,那么需要将这个左子节点适当地连接到树上,通常是连接到继承者原来位置的父节点上。
此外还可以使用左子树的最大节点来替换:
使用待删除节点左子树的最大值(在这个例子中是17)来替换待删除节点(20),也是完全有效的。实际上,当删除一个有两个子节点的节点时,您可以选择要么使用其右子树中的最小节点,要么使用其左子树中的最大节点来替代。这两种方法都能保持二叉查找树的属性。
使用左子树的最大节点作为替代者的步骤:
- 找到要删除的节点:节点
20。 - 找到继承者:节点
20的左子树中的最大节点是17。 - 删除继承者原节点:将节点
17从其原位置删除。在这个例子中,17似乎没有子节点,因此可以直接删除。 - 替换被删除节点:将
17放到20的位置,并调整其左右子节点的链接。
删除和替换后的树如下所示:
15
/ \
10 17
\
25
在这种情况下,因为 17 没有子节点,所以替换过程比较简单。如果 17 有子节点,通常是一个左子节点,那么这个左子节点需要适当地连接到树上,通常是连接到 17 原来位置的父节点上。
无论是选择右子树的最小节点还是左子树的最大节点作为替换节点,都是基于同样的原因:这两个节点都最多只有一个子节点,这使得替换过程更为简单。
右子树的最小节点
- 位置:位于右子树的最左侧。
- 特点:由于是最小节点,因此它不会有左子节点(有左子节点的话,那个左子节点会更小)。
- 处理:删除这个节点时,如果它有右子节点,那么这个右子节点将取代它的位置。
左子树的最大节点
- 位置:位于左子树的最右侧。
- 特点:由于是最大节点,因此它不会有右子节点(有右子节点的话,那个右子节点会更大)。
- 处理:删除这个节点时,如果它有左子节点,那么这个左子节点将取代它的位置。
在两种情况下,被替换的节点(右子树的最小节点或左子树的最大节点)都只需处理一个子节点(或没有子节点),这简化了替换过程。最终选择哪种方法,可能取决于具体实现的偏好或者特定场景下的考虑(比如树的平衡性)。在实际操作中,两种方法都是可行的,并且都能保持二叉查找树的性质。
4. 案例*:删除二叉查找树中的某个节点的代码示例
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def deleteNode(root, target):
if root is None:
return root
print("Visiting node:", root.value) # For demonstration
# 找到要删除的节点
if target < root.value:
root.left = deleteNode(root.left, target)
elif target > root.value:
root.right = deleteNode(root.right, target)
else:
# 节点为叶子节点或只有一个子节点
if root.left is None:
return root.right
elif root.right is None:
return root.left
# 节点有两个子节点,找到右子树中的最小节点
minNode = findMin(root.right)
root.value = minNode.value
root.right = deleteNode(root.right, minNode.value)
return root
def findMin(node):
while node.left is not None:
node = node.left
return node
# 插入代码,展示代码,以及构建二叉搜索树示例
# Helper function to insert nodes in BST
def insertNode(root, value):
if root is None:
return TreeNode(value)
if value < root.value:
root.left = insertNode(root.left, value)
else:
root.right = insertNode(root.right, value)
return root
# Function to print the tree in order (for visualization)
def printTree(root, depth=0, prefix="Root: "):
if root is not None:
print(" " * depth * 2 + prefix + str(root.value))
printTree(root.left, depth + 1, "L--- ")
printTree(root.right, depth + 1, "R--- ")
# Creating the example tree
root = None
for value in [10, 5, 15, 3, 7, 20]:
root = insertNode(root, value)
# Print the initial tree
printTree(root)
Root: 10
L--- 5
L--- 3
R--- 7
R--- 15
R--- 20
# 删除叶子节点
# Deleting a leaf node (7)
print("Deleting leaf node 7:")
root = deleteNode(root, 7)
printTree(root)
Deleting leaf node 7:
Root: 10
L--- 5
L--- 3
R--- 15
R--- 20
# 删除只有一个子节点的节点
# Deleting a leaf node (15)
print("Deleting leaf node 15:")
root = deleteNode(root, 15)
printTree(root)
Deleting leaf node 15:
Root: 10
L--- 5
L--- 3
R--- 20
# 删除有两个子节点的节点
# Deleting a node with two children (10)
print("Deleting node with two children 10:")
root = deleteNode(root, 10)
printTree(root)
Deleting node with two children 10:
Root: 20
L--- 5
L--- 3
下边展示了上述二叉搜索树(BST)示例,并展示在删除不同类型节点时的递归过程。我们的示例树将包含多种情况:叶子节点、仅有一个子节点的节点以及有两个子节点的节点。
示例树结构
为了简单明了,我会构建如下的树:
10
/ \
5 15
/ \ \
3 7 20
在这个树中,节点 3 和 7 是叶子节点,节点 15 有一个右子节点 20,而节点 10 和 5 都有两个子节点。
演示删除操作
- 删除叶子节点:比如删除节点 7。
- 删除只有一个子节点的节点:比如删除节点 15。
- 删除有两个子节点的节点:比如删除节点 10。
我将按照这个顺序逐步构建并演示树的状态。首先,让我们创建这个树的实例。
我们已经创建了以下的二叉搜索树:
10
/ \
5 15
/ \ \
3 7 20
现在,让我们逐一演示删除操作:
- 删除叶子节点:我们将删除节点 7 并展示树的变化。
- 删除只有一个子节点的节点:接着我们将删除节点 15 并展示树的变化。
- 删除有两个子节点的节点:最后,我们将删除节点 10 并展示树的变化。
为了展示这些删除操作的递归过程,我将修改 deleteNode 函数,使其在每一步骤中打印出当前的递归状态。我们首先从删除叶子节点 7 开始。
删除叶子节点 7 的递归过程如下:
- 访问根节点 10。
- 因为 7 小于 10,所以递归地访问左子节点 5。
- 接着因为 7 大于 5,递归地访问右子节点 7。
- 找到目标节点 7(它是叶子节点),所以直接删除。
删除节点 7 后的树结构变为:
10
/ \
5 15
/ \
3 20
接下来,我们将演示删除只有一个子节点的节点,即删除节点 15。
删除只有一个子节点的节点 15 的递归过程如下:
- 访问根节点 10。
- 因为 15 大于 10,所以递归地访问右子节点 15。
- 找到目标节点 15(它只有一个右子节点 20),所以用子节点 20 替换它。
删除节点 15 后的树结构变为:
10
/ \
5 20
/
3
最后,我们将演示删除有两个子节点的节点,即删除节点 10。这是最复杂的情况,因为需要找到右子树中的最小节点来替换被删除节点的值。
删除有两个子节点的节点 10 的递归过程如下:
- 访问根节点 10。
- 找到目标节点 10,它有两个子节点。
- 在右子树中找到最小节点,即 20(在这种特殊情况下,20 直接是 10 的右子节点,因为 15 已被删除)。
- 将 10 的值替换为 20,并在右子树中删除节点 20。
- 在删除 20 时,再次访问节点 20,但这次它是叶子节点或只有一个子节点的情况。
删除节点 10 后,20 成为了新的根节点,树结构变为:
20
/
5
/
3
这样我们就完成了三种不同类型节点的删除演示:叶子节点、只有一个子节点的节点、以及有两个子节点的节点。每种情况的递归过程都有所不同,体现了二叉搜索树删除操作的多样性。
5. 案例:二叉查找树的算法(4的总结)
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def insert(root, key):
if root is None:
return TreeNode(key)
if key < root.key:
root.left = insert(root.left, key)
elif key > root.key:
root.right = insert(root.right, key)
return root
def search(root, key):
if root is None or root.key == key:
return root
if key < root.key:
return search(root.left, key)
return search(root.right, key)
def delete(root, key):
if root is None:
return root
if key < root.key:
root.left = delete(root.left, key)
elif key > root.key:
root.right = delete(root.right, key)
else:
if root.left is None:
return root.right
elif root.right is None:
return root.left
temp = minValueNode(root.right)
root.key = temp.key
root.right = delete(root.right, temp.key)
return root
def minValueNode(node):
current = node
while current.left is not None:
current = current.left
return current
6. 案例*: 如何利用二叉查找树实现“商城查找”业务需求
业务背景 :
一个网上商城需要维护一张用户表,记录了每个用户的用户名和密码。请使用二叉查找树实现用户的注册和登录功能。注册时将用户信息插入二叉查找树中,并能够检查用户名是否已经存在;登录时检查用户名是否存在并比对密码是否正确。
class UserNode:
"""
二叉查找树节点,保存用户的信息
"""
def __init__(self, username, password):
self.username = username # 用户名
self.password = password # 密码
self.left = None # 左子节点
self.right = None # 右子节点
class UserTree:
"""
用户查找树,实现用户的注册和登录功能
"""
def __init__(self):
self.root = None # 根节点
def insert(self, username, password):
"""
将新用户信息插入到树中
"""
if not self.root: # 如果树为空,创建一个新节点作为根节点
self.root = UserNode(username, password)
else:
current = self.root # 从根节点开始往下遍历
while True:
if username < current.username: # 用户名比当前节点小,继续往左子树遍历
if current.left:
current = current.left
else:
current.left = UserNode(username, password) # 找到合适的位置,插入新节点
break
elif username > current.username: # 用户名比当前节点大,往右子树遍历
if current.right:
current = current.right
else:
current.right = UserNode(username, password) # 找到合适的位置,插入新节点
break
else: # 用户名已经存在,抛出异常
raise ValueError("Username already exists")
def search(self, username, password):
"""
在树中查找用户,如果找到且密码匹配,则返回True,否则返回False
"""
current = self.root # 从根节点开始查找
while current:
if username == current.username: # 找到了目标节点
return password == current.password # 如果密码匹配,则返回True,否则返回False
elif username < current.username: # 往左子树查找
current = current.left
else: # 往右子树查找
current = current.right
return False # 没找到目标节点,返回False
UserNode 类表示了二叉查找树的节点,存储了用户名和密码信息。UserTree 类实现了用户的注册和登录功能,通过插入操作将新用户信息插入到树中,并通过搜索操作查找指定用户并验证密码。
insert 方法将新用户信息插入到树中。如果树为空,则创建一个新节点作为根节点。否则,根据用户名比较大小,从根节点开始向下遍历树,找到合适的位置将新节点插入。
search 方法用于在树中查找用户。从根节点开始,根据用户名比较大小,往左子树或右子树遍历,直到找到目标节点或遍历到叶子节点为止。如果找到目标节点,则比较输入的密码和目标节点的密码是否匹配,如果匹配则返回 True,否则返回 False。
这样,通过 UserTree 类可以实现用户的注册和登录功能。
7. 闯关题
根据要求完成题目
Q1. (单选)下面哪个操作不属于二叉查找树的基本操作?
A. 插入节点
B. 查找节点
C. 删除节点
D. 旋转节点
Q2. (单选)二叉查找树是一种支持快速查询的数据结构,在实际应用中被广泛使用。下面哪个应用领域不适合使用二叉查找树?
A. 数据库索引
B. 字典树
C. 网络路由算法
D. 操作系统进程调度算法
Q3.(判断对错) 二叉查找树的每个节点都只有一个子节点 (T/F)
Q4.(判断对错) 二叉查找树中,删除某个节点时只需考虑该节点的左右子节点 (T/F)
案例*:二叉查找树实现简单的联系人管理系统的实现代码
# 定义联系人类
class Contact:
def __init__(self, name, phone):
self.name = name
self.phone = phone
# 定义二叉查找树节点类
class TreeNode:
def __init__(self, contact):
self.contact = contact
self.left = None
self.right = None
# 定义联系人管理系统类
class ContactManager:
def __init__(self):
self.root = None
# 插入联系人
# 插入联系人
def insert(self, contact):
newNode = TreeNode(contact) # 创建一个新的二叉查找树节点来存储联系人信息
if self.root is None: # 判断根节点是否为空
self.root = newNode # 题目q5 : 如果为空,将根节点指向新节点
else:
currNode = self.root # 如果根节点不为空,从根节点开始遍历二叉查找树
while True:
# 根据联系人的名称比较大小来确定插入到左子树还是右子树
if contact.name < currNode.contact.name: # 比较要插入的联系人名称与当前节点的联系人名称
if currNode.left is None: # 如果当前节点的左子树为空
currNode.left = newNode # 将新节点插入到当前节点的左子节点位置
break # 中断循环
else:
currNode = currNode.left # 继续遍历左子树
else: # 如果要插入的联系人名称大于等于当前节点的联系人名称
if currNode.right is None: # 如果当前节点的右子树为空
currNode.right = newNode # 题目q6 : 将新节点插入到当前节点的右子节点位置
break # 中断循环
else:
currNode = currNode.right # 继续遍历右子树
# 查找联系人
def find(self, name):
if self.root is None:
return None
currNode = self.root
while currNode is not None:
# 判断当前节点的联系人名称与目标名称的大小关系
if name == currNode.contact.name:
return currNode.contact
elif name < currNode.contact.name:
currNode = currNode.left
else:
currNode = currNode.right
return None
# 创建联系人管理系统实例
contactManager = ContactManager()
# 插入联系人
contact1 = Contact("Alice", "1234567890")
contactManager.insert(contact1)
contact2 = Contact("Bob", "9876543210")
contactManager.insert(contact2)
contact3 = Contact("Charlie", "2345678901")
contactManager.insert(contact3)
# 查找联系人
contact = contactManager.find("Bob")
if contact:
print("联系人名称:", contact.name)
print("联系人电话:", contact.phone)
else:
print("未找到相关联系人")
联系人名称: Bob
联系人电话: 9876543210
上面是一个如何用二叉查找树实现简单的联系人管理系统的实现代码
观察上面的代码,完成下面的单选题(注意仔细查看注释和前后代码)
Q5. 代码第25行为空,现在需要实现 如果为空,将根节点指向新节点,下面哪个选项为正确代码,选择正确选项并把结果赋值给a5
A : self.root = TreeNode
B : self.root = newNode
C : self.root = newNode()
D : self.root = TreeNode()
Q6. 代码第38行为空,现在需要实现 将新节点插入到当前节点的右子节点位置,下面哪个选项为正确代码,选择正确选项并把结果赋值给a6
A : currNode.right = TreeNode()
B : currNode.right = TreeNode
C : currNode.right = newNode
D : currNode.right = newNode()
#填入你的答案
a1 = 'D' # 如 a1 = 'A'
a2 = 'D' # 如 a2 = 'A'
a3 = 'F' # 如 a3 = 'F'
a4 = 'F' # 如 a4 = 'F'
a5 = 'B' # 如 a5 = 'A'
a6 = 'C' # 如 a6 = 'A'