协方差自适应调整的进化策略(CMA-ES)转载自知乎——补充
之前转载的原文好像挂了,于是在知乎上又找了一篇相关的文章,原文链接为:https://zhuanlan.zhihu.com/p/150946035
本文仅作个人学习用,若有侵权请联系删除
目录
什么是进化策略
简单高斯进化策略
协方差自适应进化策略
基本原理
更新均值
控制步长
自适应协方差矩阵
本文翻译自:https://lilianweng.github.io/lil-log/2019/09/05/evolution-strategies.html,这篇博文很早就看过,但是每次都是似懂非懂,各种数学公式,虽然我做这个方向的研究很久,但是仍然不能全懂。这个端午,闲来无事,便萌生了翻译的念头,在此分享给各位对这个方向感兴趣的同学们。进化计算近年来的应用领域也一直被拓展,在很多领域展现了很好的性能,是个不错的研究方向。当研究到Fisher信息矩阵时竟发现与几何流形竟也有一定的相关性。深知知识的相通性,学海无涯,希望能再接再厉,对这一领域探知一二。
在学习最优模型参数时,梯度下降不是唯一的选择。在我们不知道目标函数的精确解析形式或不能直接计算梯度的情况下,进化策略(ES)是有效的。这篇文章深入探讨了几个经典的ES方法,以及如何在深度强化学习中使用ES。
随机梯度下降是优化深度学习模型的普遍选择。然而,这并不是唯一的选择。在黑盒优化算法中,可以评估目标函数![]() ,即使你不知道目标函数精确的解析形式,因此无需计算梯度或海赛矩阵。黑箱优化方法的实例有模拟退火法、爬坡法和 Nelder-Mead method等一系列算法。
,即使你不知道目标函数精确的解析形式,因此无需计算梯度或海赛矩阵。黑箱优化方法的实例有模拟退火法、爬坡法和 Nelder-Mead method等一系列算法。
进化策略(ES)是一种黑箱优化算法,诞生于进化算法(EA)家族。这篇文章将深入介绍一些经典的ES方法,并介绍ES如何在深度强化学习中发挥作用的一些应用。
什么是进化策略
进化策略(ES)属于进化算法的大家庭。ES的优化目标是实数的向量,![]() 。
。
进化算法是一种基于种群划分的优化算法,其灵感来自自然选择。自然选择认为,具有有利于生存的特性的个体可以世代生存,并将好的特性传给下一代。进化是在选择过程中逐渐发生的,进化使种群生长得能更好地适应环境。
![]()
进化算法作为一种通用的优化方案,可以归纳为以下格式:
假设我们想优化一个函数f(x)但f(x)的梯度难以求解。只能得到在特定x下f(x)的确定值。
我们认为随机变量 x 的概率分布![]() 是函数 f (x) 优化问题的一个较优的解,θ 是分布
是函数 f (x) 优化问题的一个较优的解,θ 是分布![]() 的参数。j我们最终的目标是找到 θ 的最优设置。
的参数。j我们最终的目标是找到 θ 的最优设置。
在给定固定分布形式(例如,高斯分布)的情况下,参数 θ 包含了最优解的知识,在一代与一代间进行迭代更新。
初始化参数θ,我们可以连续地更新θ通过以下三步循环:
- 产生初始采样种群

- 评估采样种群的”适应度“值。
- 选择最优子集来更新参数θ,最优子集的选择通常是根据适应度值或者是排序。
简单高斯进化策略
简单高斯进化策略是进化策略的最基础和最经典的版本。它将![]() 建模为一个n维的各向同性的高斯分布,在高斯分布中 θ 指的是均值
建模为一个n维的各向同性的高斯分布,在高斯分布中 θ 指的是均值![]() 和标准差
和标准差![]()
![]()
简单高斯进化策略的流程如下,给定![]() :
:
- 初始化参数
 ,计数器t=0
,计数器t=0 - 从高斯分布中采样种群大小为
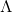 的后代种群:
的后代种群: 
- 选择出使得
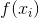 最优的 λ 个样本组成的子集,该子集被称为「精英集」。为了不失一般性,我们可以考虑 D(t+1) 中适应度排名靠前的 k 个样本,将它们放入「精英集」。我们可以将其标注为:
最优的 λ 个样本组成的子集,该子集被称为「精英集」。为了不失一般性,我们可以考虑 D(t+1) 中适应度排名靠前的 k 个样本,将它们放入「精英集」。我们可以将其标注为: 
- 选择出使得
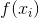 最优的 λ 个样本组成的子集,该子集被称为「精英集」。为了不失一般性,我们可以考虑 D(t+1) 中适应度排名靠前的 k 个样本,将它们放入「精英集」。我们可以将其标注为:
最优的 λ 个样本组成的子集,该子集被称为「精英集」。为了不失一般性,我们可以考虑 D(t+1) 中适应度排名靠前的 k 个样本,将它们放入「精英集」。我们可以将其标注为: 
- 重复(2)-(4)步直到结果足够好。
协方差自适应进化策略
基本原理
标准差 σ 决定了探索的程度:当 σ 越大时,我们就可以在更大的搜索空间中对后代种群进行采样。在简单高斯演化策略中,σ(t+1) 与 σ(t) 密切相关,因此算法不能在需要时(即置信度改变时)迅速调整探索空间。
「协方差矩阵自适应演化策略」(CMA-ES)通过使用协方差矩阵 C 跟踪分布上得到的样本两两之间的依赖关系,解决了这一问题。新的分布参数变为了:
![]()
其中,σ 控制分布的整体尺度,我们通常称之为「步长」。
在我们深入研究 CMA-ES 中的参数更新方法前,不妨先回顾一下多元高斯分布中协方差矩阵的工作原理。作为一个对称阵,协方差矩阵 C 有下列良好的性质:
- C 始终是对角阵
- C 始终是半正定矩阵
- 所有的特征值都是非负实数
- 所有特征值都是正交的
- C 的特征向量可以组成 Rn 的一个标准正交基
令矩阵 C 有一个特征向量 ![]() 组成的标准正交基,相应的特征值分别为
组成的标准正交基,相应的特征值分别为![]() 令 D=diag (λ1,…,λn)。
令 D=diag (λ1,…,λn)。
![]()
C 的平方根为:
![]()
相关的符号和意义如下:
![]()
更新均值
![]()
CMA-ES 使用![]() 的学习率控制均值 μ 更新的速度。通常情况下,该学习率被设置为1,从而使上述等式与简单高斯演化策略中的均值更新方法相同。
的学习率控制均值 μ 更新的速度。通常情况下,该学习率被设置为1,从而使上述等式与简单高斯演化策略中的均值更新方法相同。
控制步长
采样过程可以与均值和标准差的更新解耦:
![]()
参数 σ 控制着分布的整体尺度。它是从协方差矩阵中分离出来的,所以我们可以比改变完整的协方差更快地改变步长。步长较大会导致参数更新较快。为了评估当前的步长是否合适,CMA-ES 通过将连续的移动步长序列相加![]() 构建了一个演化路径(evolution path)
构建了一个演化路径(evolution path)![]() 通过比较该路径与随机选择(意味着每一步之间是不相关的)状态下期望会生成的路径长度,我们可以相应地调整 σ(详见下图)。
通过比较该路径与随机选择(意味着每一步之间是不相关的)状态下期望会生成的路径长度,我们可以相应地调整 σ(详见下图)。
![]()
每次演化路径都会以同代中的平均移动步长![]() 进行更新。
进行更新。
![]()
通过与![]() 相乘,我们将演化路径转化为与其方向相独立的形式。
相乘,我们将演化路径转化为与其方向相独立的形式。
![]() 原理如下:
原理如下:
- B(t) 包含 C 的特征向量的行向量。它将原始空间投影到了正交的主轴上。
-
 将各主轴的长度放缩到相等的状态。
将各主轴的长度放缩到相等的状态。 -
 将空间转换回原始坐标系.
将空间转换回原始坐标系.
为了给最近几代的种群赋予更高的权重,我们使用了「Polyak 平均 」算法(平均优化算法在参数空间访问轨迹中的几个点),以学习率![]() 更新演化路径。同时,我们平衡了权重,从而使
更新演化路径。同时,我们平衡了权重,从而使![]() 在更新前和更新后都为服从 N (0,I) 的共轭分布(更新前后的先验分布和后验分布类型相同)。
在更新前和更新后都为服从 N (0,I) 的共轭分布(更新前后的先验分布和后验分布类型相同)。
![]()
随机选择得到的![]() 的期望长度为 E‖N (0,I)‖,该值是服从 N (0,I) 的随机变量的 L2 范数的数学期望。按照图 2 中的思路,我们将根据 ‖pσ(t+1)‖/E‖N (0,I)‖ 的比值调整步长:
的期望长度为 E‖N (0,I)‖,该值是服从 N (0,I) 的随机变量的 L2 范数的数学期望。按照图 2 中的思路,我们将根据 ‖pσ(t+1)‖/E‖N (0,I)‖ 的比值调整步长:
![]()
自适应协方差矩阵
我们可以使用精英样本的![]() 从头开始估计协方差矩阵
从头开始估计协方差矩阵![]()
![]()
只有当我们选择出的种群足够大,上述估计才可靠。然而,在每一代中,我们确实希望使用较小的样本种群进行快速的迭代。这就是 CMA-ES 发明了一种更加可靠,但同时也更加复杂的方式去更新 C 的原因。它包含两种独立的演化路径:
- 秩 min (λ, n) 更新:使用 {
 } 中的历史,在每一代中都是从头开始估计的。
} 中的历史,在每一代中都是从头开始估计的。 - 秩 1 更新:根据历史估计移动步长
 以及符号信息
以及符号信息
第一条路径根据 {![]() }的全部历史考虑 C 的估计。例如,如果我们拥有很多代种群的经验,
}的全部历史考虑 C 的估计。例如,如果我们拥有很多代种群的经验,
![]() 就是一种很好的估计方式。类似于
就是一种很好的估计方式。类似于![]() ,我们也可以使用「polyak」平均,并且通过学习率引入历史信息:
,我们也可以使用「polyak」平均,并且通过学习率引入历史信息:
![]()
通常我们选择的学习率为:![]()
第二条路径试图解决![]() 丢失符号信息的问题。与我们调整步长 σ 的方法相类似,我们使用了一个演化路径
丢失符号信息的问题。与我们调整步长 σ 的方法相类似,我们使用了一个演化路径![]() 来记录符号信息,
来记录符号信息,![]() 仍然是种群更新前后都服从于 N (0,C) 的共轭分布。
仍然是种群更新前后都服从于 N (0,C) 的共轭分布。
我们可以认为我们可以认为![]() 是另一种计算
是另一种计算![]() 的(请注意它们都服从于 N (0,C)),此时我们使用了完整的历史信息,并且能够保留符号信息。请注意,在上一节中,我们已经知道了是另一种计算 的(请注意它们都服从于 N (0,C)),此时我们使用了完整的历史信息,并且能够保留符号信息。请注意,在上一节中,我们已经知道了
的(请注意它们都服从于 N (0,C)),此时我们使用了完整的历史信息,并且能够保留符号信息。请注意,在上一节中,我们已经知道了是另一种计算 的(请注意它们都服从于 N (0,C)),此时我们使用了完整的历史信息,并且能够保留符号信息。请注意,在上一节中,我们已经知道了
![]()
的计算方法如下:
![]()
接下来,通过![]() 来更新协方差矩阵:
来更新协方差矩阵:
![]()
当 k 较小时,秩 1 更新方法相较于秩 min (λ, n) 更新有很大的性能提升。这是因为我们在这里利用了移动步长的符号信息和连续步骤之间的相关性,而且这些信息可以随着种群的更新被一代一代传递下去。
最后,我们将两种方法结合起来:
![]()
![]()
在上面所有的例子中,我们认为每个优秀的样本对于权重的贡献是相等的,都为 1/λ。该过程可以很容易地被扩展至根据具体表现为抽样得到的样本赋予不同权重![]() 的情况。
的情况。
![]()