2018年认证杯SPSSPRO杯数学建模B题(第一阶段)动态模糊图像全过程文档及程序

2018年认证杯SPSSPRO杯数学建模

B题 动态模糊图像

原题再现：

  人眼由于存在视觉暂留效应，所以看运动的物体时，看到的每一帧画面都包含了一段时间内 (大约 1/24 秒) 的运动过程，所以这帧画面事实上是模糊的。对电影的截图来说，动态画面的每一帧也都是模糊的，例如图 1 为某部电影截图，展现的是在高速飞行中的拍摄效果，所以俯拍到的路面字迹是模糊的。但是一般来说，电脑游戏的每一帧画面都是以清晰的静态方式绘制出的，所以需要较高的帧率才能感觉到平滑，否则感觉会不够流畅。为了以较低的帧率能够取得较流畅的感受，在计算机视觉技术中，人们开发出了能够模拟动态模糊效果的算法。
  第一阶段问题： 当我们给出一张动态模糊的图片时，很难看清被摄景观的细节。请设计合理的数学模型，以恢复出尽可能清晰的画面。为简单起见，我们可以假设摄像机的运动导致了模糊，也就是图中的全部景观都以一个相同的速度运动。在论文中可以使用图 1，也可以另行选用动态模糊的图像作为算例。

整体求解过程概述(摘要)

  为了以较低的帧率能够取得较流畅的感受，在计算机视觉技术中，人们开发出了能够模拟动态模糊效果的算法。在此我们假设摄像机的运动导致了模糊，也就是图中的全部景观都以一个相同的速度运动，利用模糊图像复原算法复原出高清晰、高分辨率的图像。
  针对问题一建立 PSF 点扩散函数：通过采取傅里叶变换得到图片每点处的梯度大小，用来反映三维图像中的第三个量，然后灰度化处理频谱图S(, )。以 R、G、B 为轴建立空间直角坐标系，结合 Radon 变换计算图像矩阵在某一特定方向的积分，较准确的得出运动模糊图像运动方向。
  针对问题二同样建立 PSF 点扩散函数：利用得到二维模糊图像的一维频谱图像S，将二维问题降维成一维问题并结合估计出的运动方向角度，将频谱图像反向旋转。对旋转后的一维频谱图像S进行 SPF 滤波与二值化处理,按列累加进行微分运算计算出自相关图像，估计出拍摄的物体与实际物体的位移差L。
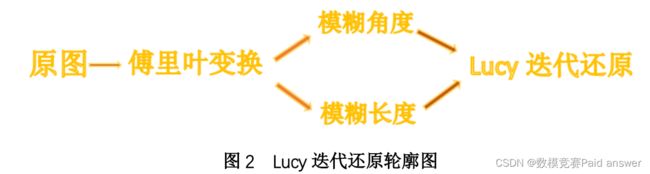
  针对问题三建立点扩展函数：利用问题一、二所求的模糊方向和模糊尺度，建立相应的运动模糊图像点扩展函数。用 Lucy-Richardson 滤波算法建立基于MATLAB 平台的仿真对附件图片 1 进行复原。引入 PSNR 的定义将图像的清晰度与其相关联，分析清晰度与迭代次数的相关性，进而转化为分析迭代次数与 PSNR 的大小之间的关系，简化了模型。
  针对问题四将小波变换理论与 Lucy-Richardson 算法相结合：选取适当的阀值将图片进行多级分解，并将每一级的高低频部分单独分离：将低频部分与 L-R 算法结合利用 Lucy-Richardson 算法恢复图像；高频部分进行阀值降噪后，将噪声分离出去，最大可能地降低噪声对 Lucy-Richardson 算法的影响。在多次分级运算后，高低频的不同频域采取不同的复原方法，完成对模糊图片的复原。

问题分析：

  问题一的分析
  为了减少所拍图片的还原难度，我们需要得出拍摄相机与物体之间的模糊角度，通过这个角度我们可以更好的沿着指定方向进行还原。首先我们要创建出图片退化的线性数学模型，接着选择准则函数，并以适当的数学形式表达，然后进行数学推演。推演过程中通常要进行表达形式（即空域形式、频域形式、矩阵-矢量形式或变换域形式）的相互转换，最后得到图像复原的公式。

  就一张单纯图片而言，我们无法得知这张图片的频率大小，因为所拍摄的物体是空间的，而图片是平面的。因此需要引入第三个量，使图片能够反映出三维的信息。通过查阅相关资料，我们可以用梯度来反映第三个量，而我们可以通过采取傅里叶变换得到图片每点处的梯度大小。即将一些看似紊乱的函数，用很多条正弦波组合表现出来。从图片表示上，可以说是把图片上的信息用频率的方式给表示出来。表现出来的频率用灰度梯度的形式显示到电脑屏幕上。比如说，在一个温度变化不大，空间变化不大的区域如沙漠，其表现出来的灰度梯度就会比较平稳；而对于像大陆表面温度，变化是相对明显的，因此表现出来的灰度会呈现较为剧烈的现象。
  所以首先我们应该先把图形进行灰度化处理。以 R、G、B 为轴建立空间直角坐标系，则RGB图的每个象素的颜色可以用该三维空间的一个点来表示，而Gray 图的每个象素的颜色可以用直线R = G = B上的一个点来表示。于是rgb转gray 图的本质就是寻找一个三维空间到一维空间的映射，最容易想到的就是射影（即过rgb空间的一个点向直线R = G = B做垂线），事实上Matlab也是这样做的，并且有Gray = 0.29900 ∗ R + 0.58700 ∗ G + 0.11400 ∗ B。
  我们可以用matlab求出已知图像的傅里叶频谱图，其会表现出来明暗不一的亮点，这种现象就是梯度，就是这个点的频率与相邻点的频率差异大小（这里我们可以理解成空间上的高矮程度）。那么空间上的三维向量全给表现出来了。在亮度较大的地方，它的梯度也就较大；在亮度较小的地方，其梯度也就相对较小。同时，我们也能够看出能量的分布大小。如果变换后的图像亮点很多，说明原图片很多点与相邻点的梯度差异较大，说明原图像比较刺眼，比较尖锐。如果变换后的图像暗点很多，说明很多点与相邻点的梯度差异较小，说明原图像比较平稳，比较柔和。
  因为所拍图像可能含有很多外界因素的干扰。我们可以将傅里叶频谱图放在原点，这样图像就是以原点为中心对称分布。如果出现还有其他的对称点，那么这个就是干扰因素，可能受到了其他正弦函数的干扰。从图像上就可以很直观的看出图像是否收到干扰。当然这种方式只能较为粗略的观察图像的干扰情况，因此精度不高，但是也能满足实验要求了。设暗纹与x轴正向夹角为φ，运动模糊方向与x轴夹角为θ，图像尺寸为M × N,根据傅里叶变换的时频特性可以知道，可通过公式tan = tan( − 90°) × M/N 得到模糊角度 θ ,因此只要通过 Radon 变换检测出频谱暗条纹与水平方向的夹角即可到运动模糊方向。

  问题二的分析
  在多数情况下,导致运动模糊是因为拍摄的设备与场景之间的相对运动造成的，例如无人机低空侦察，抓拍高速汽车等等。这类的运动模糊都具有速度较大、曝光时间较短的特点，因而在拍摄时间内，运动看成是匀速直线运动是再合适不过了。
  本文依据运动模糊图像和原始图像在频谱上的对应关系。我们可以直接在二维方向进行考虑，但 x，y 坐标下都会有位移，不方便考虑。我们可以结合估计出的运动方向角度，对图像进行旋转变换，运用微分自相关方法，将二维问题降维成一维问题，之后应用一维频谱的方法估计出拍摄的物体与实际物体的位移差（即模糊尺度）。
  问题三的分析
  问题三在前两问的基础上，考虑到利用 Lucy-Richardson 滤波法会和点扩散函数的两个参数有关，所以基于问题一和问题二的求解结果，得到附件图片 1的模糊尺度和模糊长度，利用模糊图像的运动模糊角度和运动模糊长度，可以得到相应图片的点扩散函数。同时基于matlab软件，设计相应的程序，利用Lucy-Richardson 滤波算法对该图片进行图片复原，在复原的同时，还要考虑迭代次数对于复原图形的影响，不同的迭代次数的图片会呈现出怎么的清晰度，同时引入一个关于 PSNR 的定义，将图像的清晰度与其相关联，分析清晰度与迭代次数的相关性，也就进而转化为分析迭代次数与 PSNR 的大小之间的关系，简化了模型，使问题三进而得以解决。
  问题四的分析
  由于附录图片 1 是有噪音的运动模糊图像，在考虑该条件的同时，我们采取与问题三不同的解决方法。我们采用小波变换理论与 Lucy-Richardson 算法相结合的算法，将图片进行多级分解，并将每一级的高低频部分单独分离，对于低频的这部分，利用 Lucy-Richardson 算法恢复图像，对于高频的部分，我们进行阀值降噪，将噪声分离出去，尽最大的可能性降低噪声对 Lucy-Richardson 算法的影响，在进行多次分级运算后，高低频的不同频域采取不同的复原方法，从而在多次分级运算后，完成对模糊图片的复原。

模型假设：

  1、假设摄像机的运动导致了模糊，也就是图中的全部景观都以一个相同的速度运动。
  2、摄像机的运动是匀速的。
  3、天气晴朗照片轮廓清晰。
  4、摄像机运作正常，数据保存完整。
  5、模糊图像像素在可傅里叶变换、radon 范围内。

论文缩略图：

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

filename = 'C:\Users\hasee\Desktop\图片.jpg';
I = imread(filename);
7 
8 figure
9 imshow(uint8(I));
10 title('原图');
11 
12 %% 生成运动模糊图像
13 PSF = fspecial('motion',80, 150);
14 g = imfilter(I, PSF, 'circular');
15 figure 
16 imshow(uint8(g));
17 title('运动模糊图');
18 
19 %% 对运动模糊图像进行灰度化，并进行二维快速傅里叶变换，生成其
频谱图
20 gb = rgb2gray(g);
21 figure
22 imshow(uint8(gb));
23 PQ = paddedsize(size(gb));
24 F = fft2(gb, PQ(1), PQ(2));
25 figure
26 imshow(uint8(F));
27 
28 %% 作出倒频谱
29 F1 = log(1+abs(F));
30 F2 = abs(F1).^2;
31 F3 = real(ifft2(F2));
32 figure
33 imshow(uint8(F3));
34 
35 
36 %% 将倒频谱压缩，居中
37 H = log(1+abs(F3)); % 将倒频谱动态范围进行压缩
38 Hc = fftshift(H); % 将压缩结果进行循环移位，使低频成分居中
39 figure
40 imshow(uint8(Hc));
41 
42 %% 通过阈值处理，边缘检测“canny”算子二值化倒频谱
43 T = graythresh(Hc);
44 bw=edge(Hc, 'canny', T);

45 figure
46 imshow(bw);
47 
48 %% 对倒频谱从 1°到 180°作 radon 变换，以求出模糊角度
49 theta = 1:180;
50 R = radon(bw, theta);
51 figure
52 imshow(R);
53 
54 %% 计算出通过倒频谱 radon 变换估计出的模糊角度
55 MAX = max(max(R));
56 [m, n] = find(R == MAX);
57 if 90 < n <= 180
58 beita = n - 90;
59 else if 0 < n < 90
60 beita = n + 90;
61 else if n == [90;90] | n == [180;180]
62 beita = n(1);
63 end;

clc;
I=imread('C:\Users\lenovo\Desktop\图 1.png');
PSF1=fspecial('motion',40,100);
MF=imfilter(I,PSF1,'circular');
gb=rgb2gray(MF);
f1=im2double(gb);
h=fspecial('Sobel'); 
J=conv2(f1,h,'same'); 
IP=abs(fft2(J)); 
%图像能量谱密度
s=fftshift(real(ifft2(IP))); 
figure,plot(s);
title('自相关图');
m=size(s,1);
S=sum(s);
mid=floor(m/2);
len=0;
ru=0;l=0; p =0;q =0;
for i=mid-10:-1:2
 if (S(i+5)>S(i))&&(S(i+2)>S(i))&&(S(i-2)>S(i))&&(S(i5)>S(i))&&(S(i+10)>S(i))&&(S(i10)>S(i))&&(S(i+1)>S(i))&&(S(i+3)>S(i))&&(S(i+4)>S(i))&&(S(i-3)>S(i))&&(S(i-
4)>S(i))
 ru=i; p=p+1;
 if p==2
 break;
 end
 end
end
for i=mid+10:1:m-2
 if 
(S(i+2)>S(i))&&(S(i+1)>S(i))&&(S(i+3)>S(i))&&(S(i+4)>S(i))&&(S(i+5)>S(i))&&(
S(i-2)>S(i))&&(S(i-1)>S(i))&&(S(i-3)>S(i))&&(S(i4)>S(i))&&(S(i+10)>S(i))&&(S(i-10)>S(i))
 l=i;q = q+1;
 if q ==2
 break;
 end
 end
end
len=(l-ru)/2

j=imread('图片.jpg');
figure(1),imshow(j); 
title('原图像');
len=40;
theta=83;
PSF = fspecial('motion',len,theta);
lucy=deconvlucy(j,PSF,i);％i 为迭代次数
figure,imshow(lucy); 
title(' Lucy richardson 图像复原');
function PSNR = psnr(f1, f2)%计算两幅图像的峰值信噪比
k = 8; %k 为图像是表示每个像素点所用的二进制位数，即位深。
fmax = 2.^k - 1;
a = fmax.^2;
e = im2uint8(f1) - im2uint8(f2);
[m, n] = size(e);
b = mean(mean(e));
PSNR = 10*log10(a/(b*m*n));

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可