java数组的顺序查找、二分查找，冒泡排序、快排（超级详细，代码+图解）

一，查找

1.1 java顺序查找

顺序查找：挨个查看

要求：对数组元素的顺序没要求

public class TestArrayOrderSearch {
    //查找value第一次在数组中出现的index
    public static void main(String[] args){
        int[] arr = {4,5,6,1,9};//初始化数组
        int value = 1;//需要查找的值
        int index = -1;//初始化下标
​
        for(int i=0; i 
  

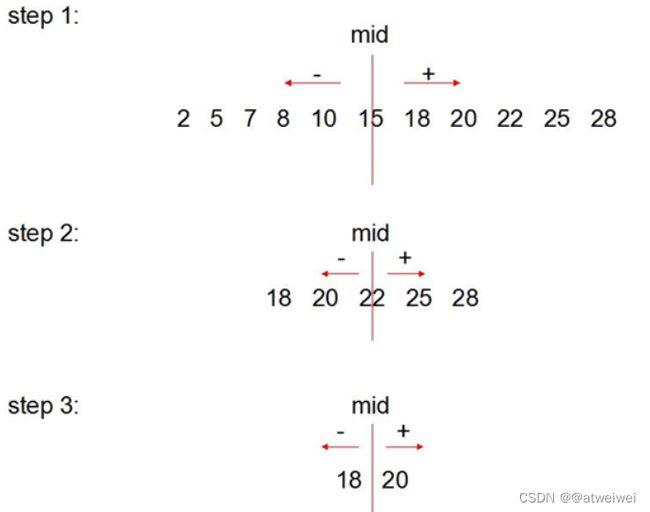
1.2 、java二分查找

举例：

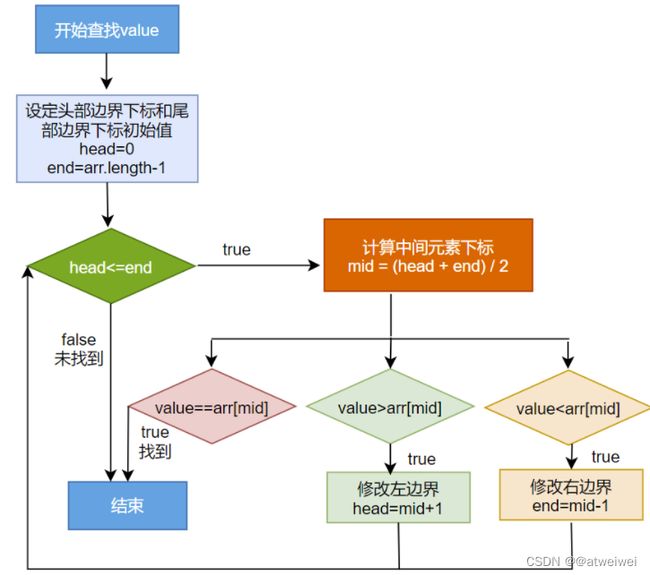
实现步骤：

//二分法查找：要求此数组必须是有序的。
int[] arr3 = new int[]{-99,-54,-2,0,2,33,43,256,999};
boolean isFlag = true;
int value = 256;//需要找的值
//int value = 25;
int head = 0;//首索引位置
int end = arr3.length - 1;//尾索引位置
while(head <= end){
    int middle = (head + end) / 2;
    if(arr3[middle] == value){
        System.out.println("找到指定的元素，索引为：" + middle);
        isFlag = false;
        break;
    }else if(arr3[middle] > value){
        end = middle - 1;
    }else{//arr3[middle] < value
        head = middle + 1;
    }
}
​
if(isFlag){
    System.out.println("未找打指定的元素");
}
​

二，排序

2.1 冒泡排序（Bubble Sort）

排序思想：

1. 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。

2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

3. 针对所有的元素重复以上的步骤，除了最后一个。

4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较为止。

 

/*
1、冒泡排序（最经典）
思想：每一次比较“相邻（位置相邻）”元素，如果它们不符合目标顺序（例如：从小到大），
     就交换它们，经过多轮比较，最终实现排序。
     （例如：从小到大）   每一轮可以把最大的沉底，或最小的冒顶。
     
过程：arr{6,9,2,9,1}  目标：从小到大
​
第一轮：
    第1次，arr[0]与arr[1]，6>9不成立，满足目标要求，不交换
    第2次，arr[1]与arr[2]，9>2成立，不满足目标要求，交换arr[1]与arr[2] {6,2,9,9,1}
    第3次，arr[2]与arr[3]，9>9不成立，满足目标要求，不交换
    第4次，arr[3]与arr[4]，9>1成立，不满足目标要求，交换arr[3]与arr[4] {6,2,9,1,9}
    第一轮所有元素{6,9,2,9,1}已经都参与了比较，结束。
    第一轮的结果：第“一”最大值9沉底（本次是后面的9沉底），即到{6,2,9,1,9}元素的最右边
​
第二轮：
    第1次，arr[0]与arr[1]，6>2成立，不满足目标要求，交换arr[0]与arr[1] {2,6,9,1,9}
    第2次，arr[1]与arr[2]，6>9不成立，满足目标要求，不交换
    第3次：arr[2]与arr[3]，9>1成立，不满足目标要求，交换arr[2]与arr[3] {2,6,1,9,9}
    第二轮未排序的所有元素 {6,2,9,1}已经都参与了比较，结束。
    第二轮的结果：第“二”最大值9沉底（本次是前面的9沉底），即到{2,6,1,9}元素的最右边
第三轮：
    第1次，arr[0]与arr[1]，2>6不成立，满足目标要求，不交换
    第2次，arr[1]与arr[2]，6>1成立，不满足目标要求，交换arr[1]与arr[2] {2,1,6,9,9}
    第三轮未排序的所有元素{2,6,1}已经都参与了比较，结束。
    第三轮的结果：第三最大值6沉底，即到 {2,1,6}元素的最右边
第四轮：
    第1次，arr[0]与arr[1]，2>1成立，不满足目标要求，交换arr[0]与arr[1] {1,2,6,9,9}
    第四轮未排序的所有元素{2,1}已经都参与了比较，结束。
    第四轮的结果：第四最大值2沉底，即到{1,2}元素的最右边
​
*/
public class Test19BubbleSort{
    public static void main(String[] args){
        int[] arr = {6,9,2,9,1};
​
        //目标：从小到大
        //冒泡排序的轮数 = 元素的总个数 - 1
        //轮数是多轮，每一轮比较的次数是多次，需要用到双重循环，即循环嵌套
        //外循环控制 轮数，内循环控制每一轮的比较次数和过程
        for(int i=1; i arr[j+1]){
                    //交换arr[j]与arr[j+1]
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
​
        //完成排序，遍历结果
        for(int i=0; i 
  
2.2 冒泡排序优化
 
  
/*
思考：冒泡排序是否可以优化
*/
class Test19BubbleSort2{
    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, 9};
​
        //从小到大排序
        for (int i = 0; i < arr.length - 1; i++) {
            boolean flag = true;//假设数组已经是有序的
            for (int j = 0; j < arr.length - 1 - i; j++) {
                //希望的是arr[j] < arr[j+1]
                if (arr[j] > arr[j + 1]) {
                    //交换arr[j]与arr[j+1]
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
​
                    flag = false;//如果元素发生了交换，那么说明数组还没有排好序
                }
            }
            if (flag) {
                break;
            }
        }
​
        //完成排序，遍历结果
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + "  ");
        }
    }
}
 
  
6.6.4 快速排序
 
  
快速排序（Quick Sort）由图灵奖获得者Tony Hoare发明，被列为20世纪十大算法之一，是迄今为止所有内排序算法中速度最快的一种，快速排序的时间复杂度为O(nlog(n))。
 
  
快速排序通常明显比同为O(nlogn)的其他算法更快，因此常被采用，而且快排采用了分治法的思想，所以在很多笔试面试中能经常看到快排的影子。
 
  
排序思想：
 
  
 
   
 
从数列中挑出一个元素，称为"基准"（pivot），
 
 
   
 
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
 
 
   
 
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
 
 
   
 
递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。
 
 
  
 
  
图示1：
 
  
 
 
  
图示2：
 
  
第一轮操作：
 
  
 
  
第二轮操作：
 
  
 
  
 
   
import java.util.Arrays;
​
public class QuickSort {
​
    // 快速排序的入口方法
    public void quickSort(int[] arr, int left, int right) {
        if (left < right) { // 当左指针小于右指针时进行排序
            int pivot = partition(arr, left, right); // 获取基准值的最终位置
            quickSort(arr, left, pivot - 1); // 对基准值左侧的子数组进行递归排序
            quickSort(arr, pivot + 1, right); // 对基准值右侧的子数组进行递归排序
        }
    }
​
    // 分区方法，用于确定基准值的最终位置
    private int partition(int[] arr, int left, int right) {
        int pivot = arr[right]; // 选择数组最后一个元素作为基准值
        int i = left - 1; // 初始化i为左指针-1
        for (int j = left; j < right; j++) { // 遍历数组中的元素（除了基准值）
            if (arr[j] < pivot) { // 如果当前元素小于基准值
                i++; // 移动i指针
                swap(arr, i, j); // 将当前元素交换到基准值左侧
            }
        }
        swap(arr, i + 1, right); // 将基准值移动到最终位置
        return i + 1; // 返回基准值的最终位置
    }
​
    // 交换数组中两个元素的方法
    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
​
    // 测试快速排序算法
    public static void main(String[] args) {
        QuickSort sorter = new QuickSort();
        int[] arr = {5, 2, 9, 3, 7, 6, 1, 8, 4};
        System.out.println("Original array: " + Arrays.toString(arr));
        sorter.quickSort(arr, 0, arr.length - 1); // 调用快速排序方法
        System.out.println("Sorted array: " + Arrays.toString(arr));
    }
}
​