数据类型、运算符
一、数据的表示详解
昨天我们学习了变量,我们知道变量可以用来记录数据的。那么数据在计算机底层是以什么形式表示的呢?下面我们就学习一下数据在计算机中的底层原理。
1.1 整数在计算机中的存储原理
其实任何数据在计算机中都是以二进制表示的。那这里肯定有人问,什么是二进制啊?所谓二进制其实就是一种数据的表示形式,它的特点是逢2进1。
数据的表示形式除了二进制(逢2进1),八进制(逢8进1)、还有十进制(逢10进1)、十六进制(逢10进1)等。
对于二进制绝大多数同学,应该是非常陌生的。 没关系!来,大家跟着我的思路,你就知道二进制是怎么表示数据的了。
1.二进制中只有0和1两个数
首先十进制的0和二进制的0是一样的,十进制的1和二进制的1也是 一样的。但是十进制中 有2,但是二进制中就没有2了
2.那么二进制是如何表示十进制的2呢?
1
+ 1
——————————
10 这里两个1相加,结果为2,由于二进制满2进1,所以最终结果10
3.那么二进制是如何表示十进制的3呢?
前面我们已经知道二进制10表示十进制的2,那么二进制10+1就表示十进制的3啊!
10
+ 1
—————————
11 十进制的3对应的二进制是11
4.那么二进制是如何表示十进制4的呢?
前面我们已经知道二进制11表示十进制的4,那么11+1就表示十进制的5啊
11
+ 1
—————————
100 十进制的5对应的二进制是100
你找到规律了吗? 你能不能依次写出5的二进制、6的二进制?
前面每算一个二进制数据都是采用+1的方式,逢2进1,一个一个算出来的。有没有更快的算出十进制对应二进制的方法呢? 这里学习一种方式:叫做除2取余法。
-
除2取余法
1.怎么做呢?
答:让十进制数据连续除以2,直到商为0,余数反转
2.举例1:把十进制6转换为二进制
商 余数
6/2 3 0+-
3/2 1 1
1/2 0 1
然后把余数反转:6对应的二进制是110
3.举例2: 把十进制13转换为二进制
商 余数
13/2 6 1
6/2 3 0
3/2 1 1
1/2 0 1
然后把余数反转:10对应的二进制是1101
4.练习1:你能把十进制7转换为二进制吗?
自己试试吧!
关于变量记录的数据在计算机中如何表示我们就先学习到这里。
-
计算机的最小存储单位
前面我们已经知道计算机表示数据是用二进制来的, 这里我又要抛出一个问题来了! 我现在想要在计算机中存储一个整数6,转换为二进制是110,那么计算机中只是存110吗三位数字吗? 其实不是的,计算机中最小的存储单位是字节(Byte),一个字节占8位(bit),也就是说即使这个数据不足8位也需要用8位来存储。
 我们随便找到一个文件,看文件的属性,可以看到文件的大小都是以字节为单位的。
我们随便找到一个文件,看文件的属性,可以看到文件的大小都是以字节为单位的。
1.2 字符在计算机中的存储原理
通过上一节的学习,我们知道了整数是如何在计算机中如何存储的?那么字符在计算机中是如何存储的呢?
其实字符并不是直接存储的,而是把每一个字符编为一个整数,存储的是字符对应整数的二进制形式。美国人搞了一套字符和整数的对应关系表,叫做ASCII编码表。
ASCII编码表中字符编码的规律:
1.字符0对应48,后面的1,2,3,4...9 对应的十进制整数依次往后顺延
2.字符a对应97,后面的b,c,d,e...z 对应的十进制整数依次往后顺延
3.字符A对应65,后面的B,C,D,E...Z 对应的十进制整数依次往后顺延
需要注意的是,在ASCII编码表中是不包含汉字的。汉字在其他编码表中,后面我们会单独介绍。关于字符在计算机中的存储学到这就可以了。
1.3 图片视频声音的存储原理
-
图片的存储
通过上面的学习我们已经知道整数和字符是如何存储的,最终都是要转换为二进制数据的,对吧! 那图片、声音、视频又是如何存储的呢?我们也来了解一下
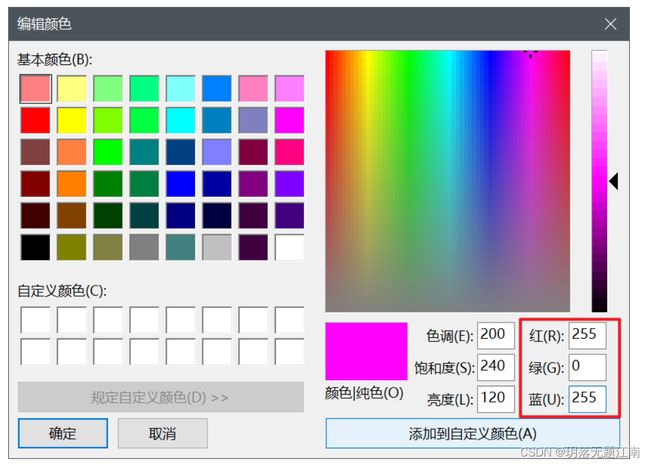
我们从图片开始,如果你把一张图片不断的放大,你会看到有马赛克的效果。你会发现图片中的每一个细节是由一个一个的小方格组成的,每一个小方格中其实就是一种颜色。任何一种颜色可以使用三原色来表示,简称RGB,其中R(红色),G(绿色),B(蓝色),而RGB中每一种颜色又用一个字节的整数来表示,最小值是0最大值是255
RGB(0,0,0)表示黑色 RGB(255,255,255)表示白色 RGB(255,0,0) 表示红色 RGB(255,255,0) 表示红色和绿色混合为黄色 RGB(255,0,255) 表示红色和蓝色混合为紫色 ...
你在画图板的颜色编辑器中可以通过指定RGB的值,来调整得到任意的颜色。一张图片实际上就是有很多个小方块的颜色组成的,而每一种颜色又是由RGB三原色的整数表示的,整数最终会转换为二进制进行存储。
实际上视频和图片是一样的,把多张图片连续播放,在一秒钟内连续播放24张以上,由于人眼存在视觉暂留现象,人眼感受不到画面切换的时间间隔,就认为是连续的视频了。
-
声音的存储
了解过物理的同学肯定知道,声音是以波的形式传播的。我们可以把声波表示在一个坐标系上,然后在坐标系上取一些点,把这些点的坐标值以二进制的形式存储到计算机中,这就是声音的存储原理。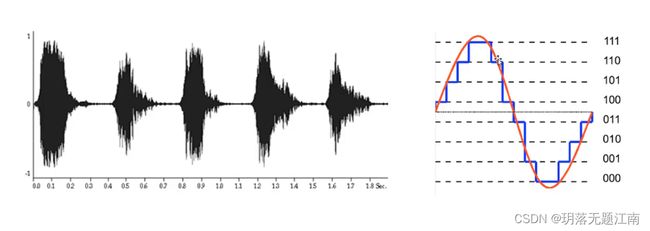
1.4 数据的其他表示形式
-
二进制到十进制的转换
前面我们学习了十进制可以转二进制,采用的是除2取余法,那么我们反过来能不能把二进制转换为十进制呢&