【数据结构】查找排序_复习笔记总结

一、查找

1. 基本概念

（1） 查找表

比如说线性表、树表、散列表

（2） 动态查找表和静态查找表

• 动态查找表：边找边操作，找到了就返回，找不到就插入
• 静态查找表：不可以操作

（3） 平均查找长度 ASL

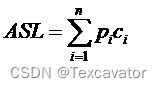
其中，P_i 为查找表中第 i 个记录的概率，C_i 为找到表中其关键字与给定值相等的第 i 个记录时比较次数。

2. 线性表的查找

（1） 顺序查找

翻译：从左到右找，相当于之前的线性表查找操作
时间复杂度： O ( n )

int Search_Seq(SSTable ST, KeyType key)
{
	for (int i = 0; i >= 0; i -- )
		if (ST.R[i].key == key) return i;
	return 0;
}

这个算法每次都要比较 i 是否大于等于1，为了避免这个检测，可以设置一个哨兵

int Search_Seq(SSTable ST, KeyType key)
{
	ST.R[0].key = key; // 监视哨
	for (int i = ST.length; ST.R[i].key != key; -- i)
		return i;
}

这样如果表中没有所求值，到0的位置就会返回0，我们也就知道已经查找完毕且没找到了，不需要去一直比较 i 和0的大小来判断是否查找完毕

（2） 折半查找 / 二分查找

考试重点！！！
时间复杂度： O ( log₂ n)
假定序列有序，先从中间开始找，如果中间值等于给定值，查找成功并返回，否则：

• 如果中间值小于给定值，说明给定值在中间值右边，所以在右半区域继续查找
• 如果中间值大于给定值，说明给定值在中间值左边，所以在左半区域继续查找

int Search_Bin(SSTable ST, KeyType key)
{
	// low到high就是目前所查找的区间
	int low = 1;
	int high = ST.length;
	while (low <= high)
	{
		int mid = low + high >> 1; // 中间值
		if (key == ST.R[mid].key) return mid;
		else if (key < ST.R[mid].key) high = mid - 1;
		else low = mid + 1;
	}
	return 0;
}

平均查找长度的计算

• 判定树
  举个栗子~
  
  这个序列的查找过程就是这个样子（这个二叉树叫做判定树）
  
  6 比较一次
  3 9 比较两次
  1 4 7 10 比较三次
  2 5 8 11 比较四次
  ASL = （1 + 2 x 2 + 3 x 4 + 4 x 4）/ 11 = 3

（3） 分块查找

时间复杂度： O ( log(m) + n / m )
又叫索引顺序查找
块间有序，块内无序
在索引表里折半查找，找到相应块后顺序查找

3. 树表的查找

（1） 二叉排序树

又叫二叉查找树

A. 定义

二叉排序树是一颗空树，或者满足：左子树比根小，右子树比根大，且左右子树都是二叉排序树
中序遍历一棵二叉排序树可以得到递增的有序序列

B. 查找

时间复杂度： 在O(n)和O(log₂ n)之间，取决于树长什么样
如果是平衡二叉树就是O(log₂ n)

思路

从根结点开始找

• 所给值等于根结点，查找成功
• 所给值小于根结点，继续查找左子树
• 所给值大于根结点，继续查找右子树

直到查找的子树为空，查找失败

代码实现

（考试不考，先挖个坑~）

C. 插入

时间复杂度： O(log₂ n)

思路

• 如果二叉树为空，就将给定值放在根结点
• 如果二叉树非空：
  • 给定值大于根结点，插入右子树
  • 给定值小于根结点，插入左子树

代码实现

（挖坑）

D. 创建

就是不断插入结点，每次插入的结点都是叶子结点，不需要移动其他结点

E. 删除

思路

首先查找带删除的结点，如果找不到就当没说，找到了就开始删：

• 如果该结点是叶子结点，直接删，即修改一下待删结点的双亲指针使它们指向NULL
• 如果该结点只有一个孩子，把孩子接到待删结点的双亲上，自己删去，也就是修改双亲指针使它们指向孩子
• 如果该结点有两个孩子，先中序遍历，然后把待删结点的直接前驱或者直接后继之间替代待删结点，然后再把原来直接前驱或者直接后继的结点删去
  举个栗子
  
  在这棵树里我们删除结点45
  先看中序遍历：3 24 37 45 50 53 100
  结点45的直接前驱和直接后继分别是37和50
  我们选择50替代45 就变成这样
  然后删去原来的结点50
  变成这样
  
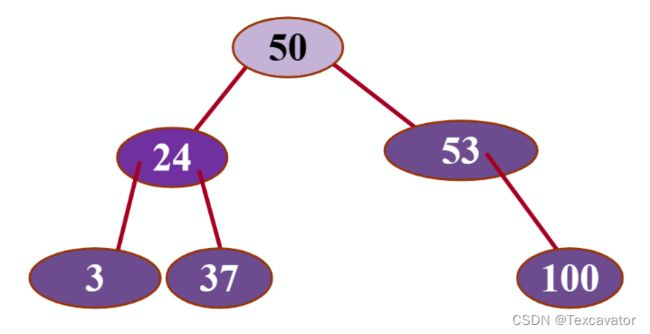
  这样也不会影响结点之间的相对顺序啦

代码实现

（挖坑）

（2） 平衡二叉树

二叉树高度越小，查找起来越快，效率就越高
高度尽可能小的二叉树叫做平衡二叉树，也叫AVL树，它有以下特点：

1. 左子树右子树的深度之差绝对值不超过1
2. 左子树和右子树也是平衡二叉树

• 平衡因子： 左右子树深度之差
  平衡二叉树的平衡因子一定只能是0、1、-1

平衡二叉树查找的时间复杂度： O (log₂ n)

调整

插入和生成都可以转化为平衡二叉树的调整问题来解决，这里就不多赘述了
平衡二叉树失去平衡后的调整可以分为以下四种情况：

i. RR型

即破坏平衡结点在右子树的右边，进行右单旋

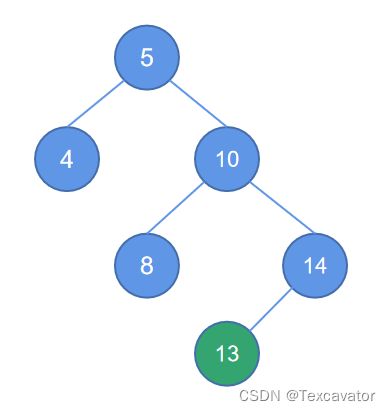
在这个例子中，找到距离13最近的被破坏的子树的根结点是5，13在5的右子树的右边
于是进行逆时针旋转，把被破坏结点的右子树变成当前二叉树的根，逆时针旋转，即将结点10变成根
此时会发现结点10的度为3（5, 8，14），就将8按照二叉排序树的规则重新插入，放在结点5的右子树位置，调整后的平衡二叉树如图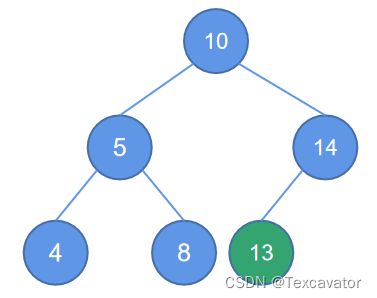

ii. LL型

即破坏平衡结点在左子树的左边，进行左单旋

在这个例子中，结点2破坏了以结点5为根的二叉树的平衡
找到距离2最近的被破坏的子树的根结点是4，2在4的左子树的左边
于是进行顺时针旋转，把被破坏结点的左子树变成当前二叉树的根，顺时针旋转，即将结点3变成根
修改后结果如图

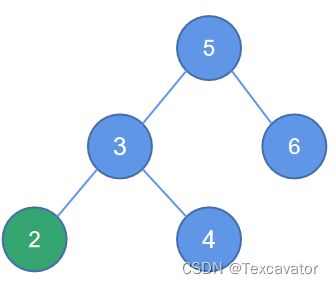
iii. LR型

即破坏平衡结点在左子树的右边，进行左右双旋

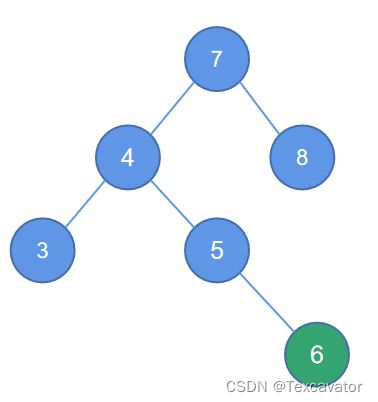
在这个例子中，结点6破坏了以结点7为根的二叉树的平衡
找到距离2最近的被破坏的子树的根结点是7，6在7的左子树的右边
于是以被破坏结点的左孩子右单旋，逆时针旋转，即变为

这个时候，破坏的结点变成了3,3破坏了以7为根的平衡二叉树，距离3最近的被破坏子树的根是7，3在7的左子树的左边，进行左单旋，调整后结果为

iv. RL型

即破坏平衡结点在右子树的左边，进行右左双旋

在这个例子中，结点5破坏了以结点3为根的二叉树的平衡
找到距离5最近的被破坏的子树的根结点是3，5在3的右子树的左边
于是以被破坏结点的右孩子左单旋，顺时针旋转，即变为

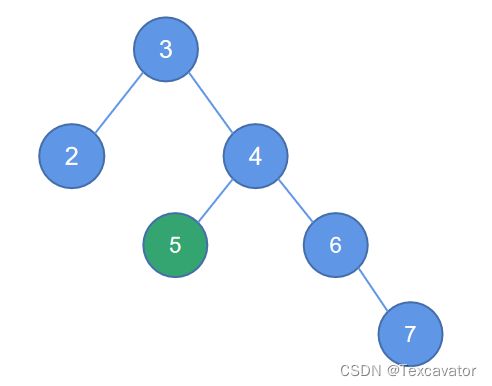
这个时候，破坏的结点变成了7,7破坏了以3为根的平衡二叉树，距离7最近的被破坏子树的根是3，7在3的右子树的右边，进行右单旋，调整后结果为

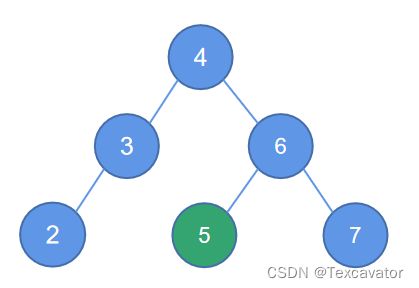
（码完才发现平衡二叉树居然不考！！可恶！！！！！）

4. 散列表的查找

• 散列表又叫哈希表，通常是一个数组存储的信息，对于不同的关键字，散列地址可能相同，此时称作冲突
• 散列表的装填因子 α
  • α = 填入表中的记录数 / 散列表的长度
  • 装填因子反应散列表的装填程度

（1） 构造方法

A. 数字分析法

事先知道关键字集合，选取重复较小的若干位作为散列地址

B. 平方取中法

如果事先不知道关键字集合，可以将关键字转换成内部编码（按自己确定的规则）然后平方，选择其中的若干位作为散列地址

C. 折叠法

如果散列地址位数较少，关键字位数较多，可以把关键字分割成位数相同的几部分，相加舍去进位，得到的值作为散列地址

D. 除留余数法

如果散列表表长为 m ，选择一个不大于 m 的 p ，用关键字除以 p ，得到的余数作为散列地址
根据经验得，p 选择小于 m 的最大质数，可以减少冲突情况

（2） 处理冲突

A. 开放寻址法

当某关键字的初始散列地址 H₀ 发生冲突，在 H₀ 的基础上计算得到新地址 H₁ ，如果还是冲突就在 H₁ 的基础上继续计算
计算公式：H_i = (H(key) + d_i) % m
其中，H(key) 为散列函数，m 为散列表表长，根据d_i 的不同，分为以下三种方式：

线性探测法

d_i = 1 …… m - 1
说人话就是当发生冲突时，从原散列地址的后一个地址开始找，遇到空的就存进去，满的就再找下一个，到最后一个都没找到空的就从头开始找

二次探测法

d_i = 1² -1² 2² -2²……

伪随机探测法

d_i = 伪随机数序列

优缺点比较

可以发现，当第 i, i + 1, i + 2 位上都有值时，下一个散列地址是 i, i + 1, i + 2 的值都存入 i + 3，这种现象叫做二次聚集

• 线性探测法
  • 线性探测法可以保证所有关键字都存进散列表
  • 线性探测法会产生二次聚集
• 二次探测法 / 伪随机探测法
  • 不保证所有关键字都能被存进散列表
  • 不会产生二次聚集

B. 链地址法

把具有相同散列地址的关键字放在一个单链表中

二、排序

1. 基本概念

排序的稳定性
假设有两个值 a b，a = b，a 在序列中的位置是 i ，b 在序列中的位置是 j
排列前 i < j，如果排序后 i 依然小于 j，说明该排序稳定，否则说明该排序不稳定

2. 插入排序

基本思想： 将每一个待排序的关键字按大小插入适当位置，直到所有关键字都被插入

（1） 直接插入排序

最简单的排序方法，思路就是从前往后，将每一个数插入前面已经排好序的序列的合适位置，到最后一个数插入完毕数列就变得有序

• 时间复杂度： O (n²)
• 空间复杂度： O (1)
• 直接插入排序是稳定的排序

举个栗子

排序（13，6，3，31，9，27，5，11）

直接插入排序过程：
【13】, 6, 3, 31, 9, 27, 5, 11
【6, 13】, 3, 31, 9, 27, 5, 11
【3, 6, 13】, 31, 9, 27, 5, 11
【3, 6, 13，31】, 9, 27, 5, 11
【3, 6, 9, 13，31】, 27, 5, 11
【3, 6, 9, 13，27, 31】, 5, 11
【3, 5, 6, 9, 13，27, 31】, 11
【3, 5, 6, 9, 11，13，27, 31】

（2） 折半插入排序

就是把直接插入排序的查找步骤换成折半查找

• 时间复杂度： O (n²)
• 空间复杂度： O (1)
• 折半插入排序是稳定的排序

（3） 希尔排序

选取增量 d ，每相隔 d 的元素分为一组，分别排序这两个数
每次缩小增量 d ，直到 d 为1

• 时间复杂度： O (nlog₂n)
• 空间复杂度： O (1)
• 希尔排序是不稳定的排序

举个栗子

排列 T=(49，38，65，97, 76, 13, 27, 49*，55, 04）

起初选取 d = 5，得到结果：

第二次选取 d = 3，得到结果：

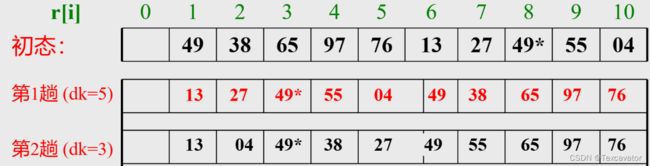
第三次选取 d = 1，得到结果：

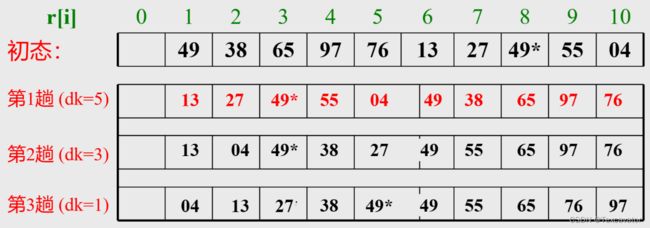
• d 较大时，组数少，排序快
• d 较小时，由于原排列已经基本有序，排序还是很快

3. 交换排序

主要思路就是两两比较待排序列，一旦发现无序就交换

（1） 冒泡排序

最简单的交换排序，两两比较相邻数据，如果是逆序就交换
每轮都可以确定一个当前序列的最小值 / 最大值

• 时间复杂度： O (n²)
• 空间复杂度： O (1)
• 冒泡排序是稳定的排序

举个栗子

排序：21，25，49， 25*，16， 08

交换过程如图所示

每次都可以确定当前待排序列的最大值

（2） 快速排序

选择序列中任意一个元素，每次排序把序列中小于它的放到前面，大于它的放到后面，形成两段，再分别递归对前后两段进行排序，直到每一段仅剩一个元素
需要使用双指针

• 时间复杂度： O (nlog₂n)
• 空间复杂度： O (log₂n)
• 快速排序是不稳定的排序

举个栗子
排序

选择第一个元素49作为分界点，把49放到0的位置，两个指针一个指队头一个指队尾

判断队尾元素，49不小于49，因此尾指针向前挪一位

27小于49，把27放到low的位置

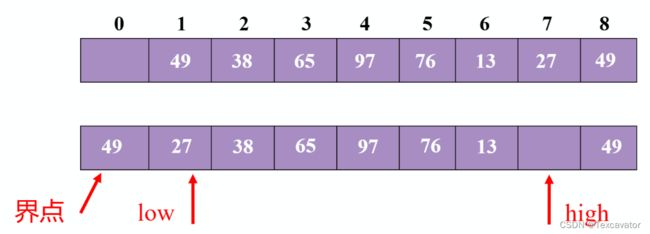
现在看头指针

38小于49，头指针往后一位

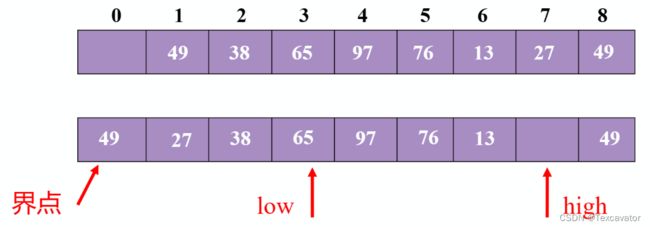
65大于49，把65挪到尾指针

尾指针往前挪一位

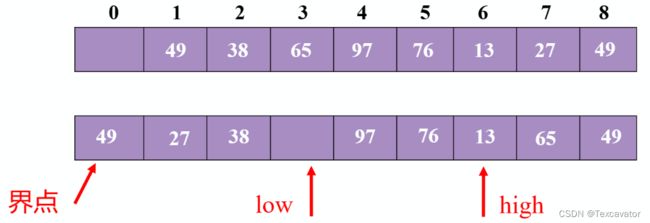
13小于49，把13挪到头指针

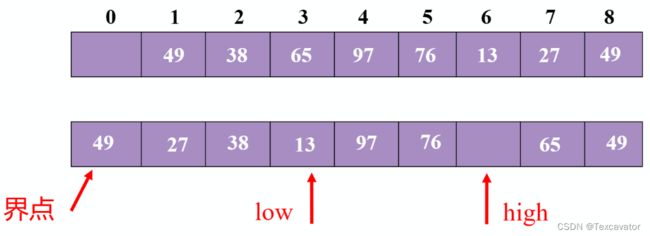
头指针往后挪一位

97大于49，把97交换到尾指针

尾指针往前挪一位

76大于49，尾指针再往前挪一位

头尾指针相遇，把49放进去

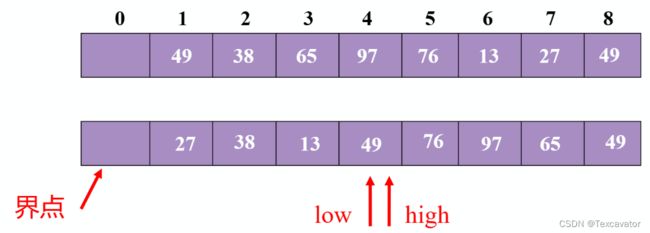
再对前半部分排序，把27确立为分界点

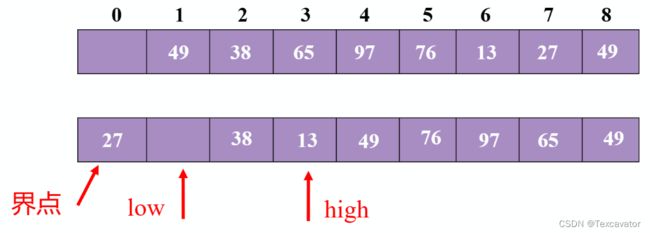
先看尾指针，13小于27，把13换到头指针，再看头指针，38大于27，把38换到尾指针，然后头尾指针相遇，把27放进去

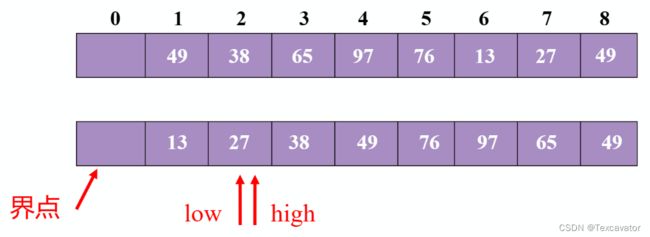
再对后半部分排序，把76确立为分界点

先看尾指针，49小于76，把49换到头指针，再看头指针，97大于76，把97换到尾指针，再看尾指针，65小于76，把65换到头指针，然后头尾指针相遇，把76放进去

再对后半部分的前半部分排序，把49确定为分界点

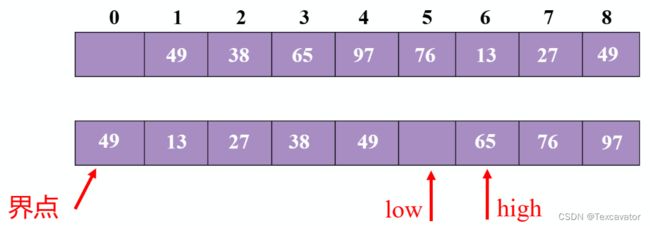
先看尾指针，65大于49，尾指针往前挪一位，头尾指针相遇，把49放进去

排序完毕~

代码实现

int Partition(SqList &L, int low, int high)
{
	L.r[0] = L.r[low];
	pivotkey = L.r[row].key;
	while (low < high)
	{
		while (low < high && L.r[high].key >= pivotkey) -- high;
		L.r[low] = L.r[high];
		while (low < high && L.r[low].key <= pivotkey) ++ low;
		L.r[high] = L.r[low];
	}
	L.r[low] = L.r[0];
	return low;
}

void QSort(SqList &L, int low, int high)
{
	if (low < high)
	{
		pivotloc = Partition(L, low, high);
		QSort(L, low, pivotloc - 1);
		QSort(L, pivotloc + 1, high);
	}
}

void QuickSort(SqList &L)
{
	QSort(L, 1, L.length);
}

4. 选择排序

（1） 简单选择排序（直接选择排序）

每次找到最小值，调到待排序列的最前面

• 时间复杂度： O (n²)
• 空间复杂度： O (1)
• 简单选择排序是不稳定的排序

（2） 树形选择排序（锦标赛排序）

利用上次的比较结果，依次输出最小值

• 时间复杂度： O (nlog₂n)
• 空间复杂度： O (n)
• 树形选择排序是稳定的排序

（3） 堆排序

树形选择排序的一种

• 大跟堆，双亲比孩子大
• 小跟堆，双亲比孩子小

这样，根一定是最大值或者最小值

• 时间复杂度： O (nlog₂n)
• 空间复杂度： O (1)
• 堆排序是不稳定的排序

A. 调整堆

输出堆顶元素后，以堆中最后一个元素替代根结点，将根结点与左、右子树根结点比较，并与大者交换重复直至叶子结点，得到新的堆
直接看例子说明吧~

把70取出后，重新调整堆

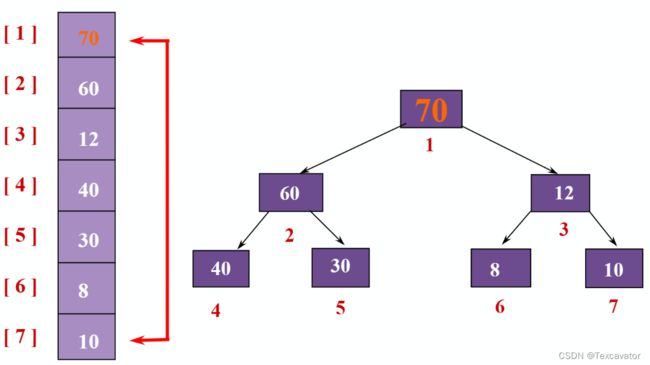
先把最后一个元素10放到原来70的位置，在10 60 12中60最大，把10和60交换，在10 40 30中40最大，把10和40交换，得到

之后的步骤类似，就不说啦

B. 建初堆

因为有n 个结点的完全二叉树，最后一个分支结点的标号是⌊n / 2⌋，所以从⌊n / 2⌋开始一直到1，依次进行调整堆就可以啦

C. 算法实现

（不考，先挖个坑）

5. 归并排序

先在序列中两个两个排序，排完合成一组，然后每两组排一次合并成一组，以此类推，直到完全遍历完

• 时间复杂度： O (nlog₂n)
• 空间复杂度： O (n)
• 归并排序是稳定的排序

看图自行理解~

6. 排序算法总结

快选堆希不稳定